基于Weibull分布的充填体单轴压缩损伤模型研究

赵树果，苏东良，吴文瑞，张亚伦

(1.华北理工大学矿业工程学院，河北 唐山 063009;2.河北省矿业开发与安全重点实验室，河北 唐山 063009)

采选技术

基于Weibull分布的充填体单轴压缩损伤模型研究

赵树果1,2，苏东良1,2，吴文瑞1，张亚伦1

(1.华北理工大学矿业工程学院，河北 唐山 063009;2.河北省矿业开发与安全重点实验室，河北 唐山 063009)

在矿山实际应力环境中，充填体多处于峰后变形阶段，研究充填体峰后强度特性对矿山安全生产十分重要。通过对灰砂比为1∶6、1∶8和1∶10的充填体试件进行单轴抗压试验，对比分析了不同灰砂比的胶结充填体变形破坏特征，灰砂比大的充填体具有更高的峰值强度和残余强度。基于统计损伤理论，确定了充填体损伤变量D并进行了修正，建立了可以表征充填体变形破坏全过程的损伤本构模型；由单轴抗压试验曲线几何特点，推导出该模型参数F0，m的数学表达式，α越小，充填体的峰后残余强度越高，F0和m越大，充填体峰值强度越大。对不同灰砂比的损伤演化规律进行了分析，各灰砂比的充填体损伤呈S型增长方式，灰砂比小的充填体能够承受更大的变形，更好的发挥其承载能力。结果表明该模型可以很好充填体破裂过程中的全应力-应变曲线和峰后残余强度的特性,为充填体强度设计提供参考。

胶结充填体；Weibull分布；Drucker-Prager准则；残余强度；损伤变量

由于国家科技水平的提高以及对环境的重视，无废开采已成为未来矿业的发展方向。充填采矿法在控制采场地压、提高资源回收率等方面有优点，得到人们的日益重视[1]。根据矿山实际情况，科学合理的确定充填体最优配比以及强度，是矿山安全生产的关键问题。在胶结充填体充入采场后，受特殊应力环境影响，充填体多处于塑性变形或峰后变形阶段，此状态下的胶结充填体并未完全丧失承载能力，损伤部分仍具有承载能力[2-3]。国内外相关研究主要侧重于胶结充填体的峰值强度与预测[4-6]，对胶结充填体的峰后力学特性研究较少[7]。在岩石混凝土方面，学者对岩石混凝土破裂全曲线尤其是峰后阶段力学特性进行了大量研究，较为系统地分析了单轴、三轴情况下的变形强度特征[8-13]。

近年来，对充填体峰值强度和配比优化的研究，在一定程度上指导了矿山安全生产，但对于充填体在的峰后阶段变形和预测研究较少。本文对灰砂比为1∶6、1∶8和1∶10胶结充填体试件进行单轴抗压试验，在试验研究的基础，引入损伤率α表征充填体峰后强度特性，建立了可以表征充填体应力-应变全曲线的统计损伤模型。对矿山充填体强度设计提供一定的指导。

1 统计损伤本构模型

1.1 损伤变量的构建

充填体在沉降过程中产生随机分布的微裂隙、微空洞是导致损伤发生的重要因素。可认为材料内部的损伤分布对材料力学性质的影响并不显著，充填体损伤为各向同性损伤问题，可用标量进行表征[14-15]。充填体在受压状态下破坏是随机发生的，其破坏概率受应力-应变状态影响显著。根据Lemaitre应变等效原理：对于受损材料，其在表观应力σ作用下，受损状态的变形等于有效应力σ*在无损状态时的变形[16]。考虑到充填体微元破坏未完全失去作用，仍继续传递部分压剪应力，本文对损伤变量进行修正，建立损伤本构方程。一维情况下的充填体损伤可定义为式(1)。

σ*=σ/(1-αD)=Eε/(1-αD)

(1)

式中：σ*为有效应力；σ为名义应力；ε为应变；α修正损伤系数；E为充填体弹性模量；D为充填体损伤变量。

充填体的损伤是由微元不断发展破裂引起的，设充填体破坏概率为P[f(σ*)]，则损伤变量D可定义为式(2)。

(2)

对于充填体微元强度的确定，结合充填体的破坏模型与判据，提出可以反应充填体微元强度的表示方法[17-18]，充填体的破坏准则通式表示为式(3)。

f(σ*)-k0=0

(3)

式中：k0为与材料性质有关的常数；σ*为充填体有效应力；F=f(σ*)表示微元强度，其形式取决于充填体破坏准则的形式。

鉴于Drucker-Prager破坏准则具有形式简单、应用广泛等特点，假定充填体微元强度满足Drucker-Prager破坏准则，见式(4)。

(4)

(5)

(6)

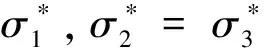
(7)

(8)

由式(7)、式(8)代入式(5)、式(6)可得式(9)、式(10)。

(9)

(10)

将式(9)、式(10)代入式(4)即得到了充填体微元强度公式。

1.2 充填体统计损伤本构模型

假定充填体微元破坏概率服从Weibull统计分布，微元尺寸既大到包含足够多的微观孔隙、裂隙，也充分小到可以认为是连续介质力学中质点的概念来考虑，其概率密度函数表示为式(11)。

(11)

式中，m、F0为Weibull分布参变量。

将式(11)代入式(2)得式(12)。

(12)

将式(7)、式(12)代入式(8)整理可得到充填体统计损伤方程见式(13)。

σ1=Eε1(1-αD)

(13)

2 充填体单轴抗压试验及破坏规律

2.1 充填体单轴抗压试验

以唐山地区某矿全尾砂作为骨料，胶结剂采用42.5#硅酸盐水泥，制备浓度为70%，灰砂比分别为1∶6、1∶8和1∶10的充填体试件，其规格为100mm×100mm×100mm。为使全尾砂水泥混合均匀，采用先干拌后湿拌的搅拌方式，将搅拌好的料浆注入模具后在室温下静置24h后脱模并编号。之后将其放置于YH-40B标准养护箱中养护28d，养护温度20℃，相对湿度95%。

单轴抗压试验在WHY-600压力机上完成，试验全程参照工程岩体试验标准(GB/T50266-99)及普通混凝土力学性能试验方法标准(GB/T50081-2002)，得到了不同灰砂比试件的荷载-位移曲线。

2.2 充填体变形破坏规律

图1为对试验数据进行处理后得到的不同灰砂比的充填体试件的应力-应变曲线。

图1 不同灰砂比充填体应力-应变曲线

由图1可将变形曲线划分四个阶段。

1)微孔隙压密阶段(O-A段)。胶结充填体在受压初期，曲线上弯，曲线切线斜率逐渐增大。充填体内部原生微裂隙、孔隙在轴向应力作用下逐渐被压密。

2)线弹性变形阶段(A-B段)。此阶段应力与应变成正比，充填体产生弹性变形。对于不同充填体试件，随灰砂比的提高，此阶段曲线斜率越大说明充填体具有更大的弹性模量。

3)非稳定破裂发展阶段(B-C段)。B点为充填体由弹性变形到塑性变形的转折点，此点为充填体屈服应力点。本阶段试件内部缺陷引起的应力集中以及裂隙面的剪切运动促使裂纹扩展。对于不同充填体试件，灰砂比越小，塑性变形阶段越明显。

4)破裂后阶段(C点以后)。充填体达到峰值荷载后，荷载随应变的增长而减小，充填体内部裂纹交汇贯通形成宏观断裂面。此时充填体仍具有部分承载能力，且随灰砂比增大，峰后曲线残余强度越大。

3 模型参数确定

由图1几何条件可得式(14)～(17)。

ε1=0，σ1=0

(14)

ε1=ε1c，σ1=σ1c

(15)

(16)

(17)

式中：σ1c为抗压强度；ε1c为抗压强度所对应的应变。

对式(13)进行求导，得到式(18)。

(18)

(19)

(20)

将边界条件式(15)代入式(13)并整理，得式(21)。

(21)

式中，Fc表示为式(22)。

(22)

整理式(21)得到式(23)、式(24)。

(23)

(24)

当σ1=σ1c时，由式(16)可得式(25)。

=0

(25)

整理式(25)得到式(26)。

(26)

将式(23)、式(24)代入式(26)并整理，得式(27)。

(27)

由式(27)、式(24)可得式(28)、式(29)。

(28)

(29)

由全尾砂胶结充填体试验曲线，可以得到充填体试件的弹性模量、极限应力及其所对应的应变，结合式(28)～式(29)得出不同损伤率α条件下的Weibull统计分布参数m、F0，见表1。代入式(13)即可得到胶结充填体的统计损伤本构方程。拟合曲线见图2。

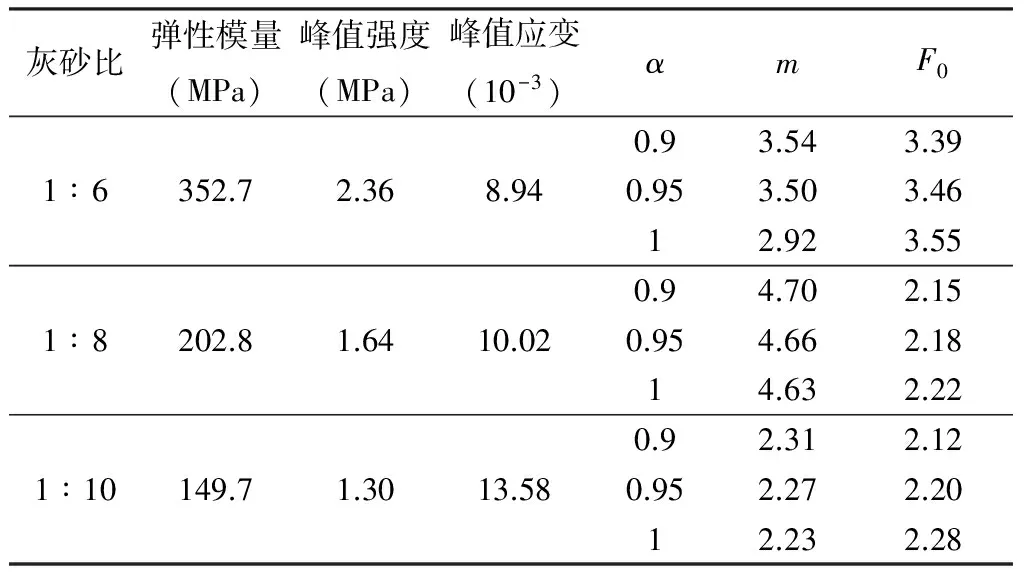
表1 统计损伤本构模型参数

采用不同的修正损伤系数对损伤变量进行修正，得到不同的损伤本构模型曲线，各灰砂比的理论曲线具有相似性(图2)。修正损伤系数α主要表征了充填体峰后残余强度特性。

1)考虑充填体破坏后仍能传递部分压剪应力，引入修正损伤系数α，建立了可以描述应力-应变全过程的修正的充填体损伤本构模型。

2)对于不同灰砂比的充填体试件，在修正损伤系数α相同的条件下，曲线具有相似形态。表明本文所引入的修正损伤系数适用于不同灰砂比的充填体本构关系建模中。

3)以灰砂比为1∶6的充填体试验曲线为例，在α=0.9的条件下，F0=3.39，m=3.54。在Weibull分布参变量m、F0不变的情况下，探讨不同修正损伤系数α对应力应变曲线的影响，如图2(a)所示。在α=1时，充填体峰后强度曲线几乎降到零，不具有残余强度，与试验所得充填体实际的应力-应变全过程曲线相差很大。在α从0.9到1的变化范围中，残余强度减小量高达96.17%，峰值强度仅减小了5.57%，而线弹性变形阶段未产生显著变化，说明修正损伤系数α主要影响充填体峰后强度阶段。

4 讨论

4.1 不同灰砂比充填体损伤过程分析

充填体损伤演化方程表示为式(30)。

(30)

由此可确定不同灰砂比试件的损伤发展规律以及充填体试件变形破坏曲线与损伤变量演化方程的关系，见图3～4。

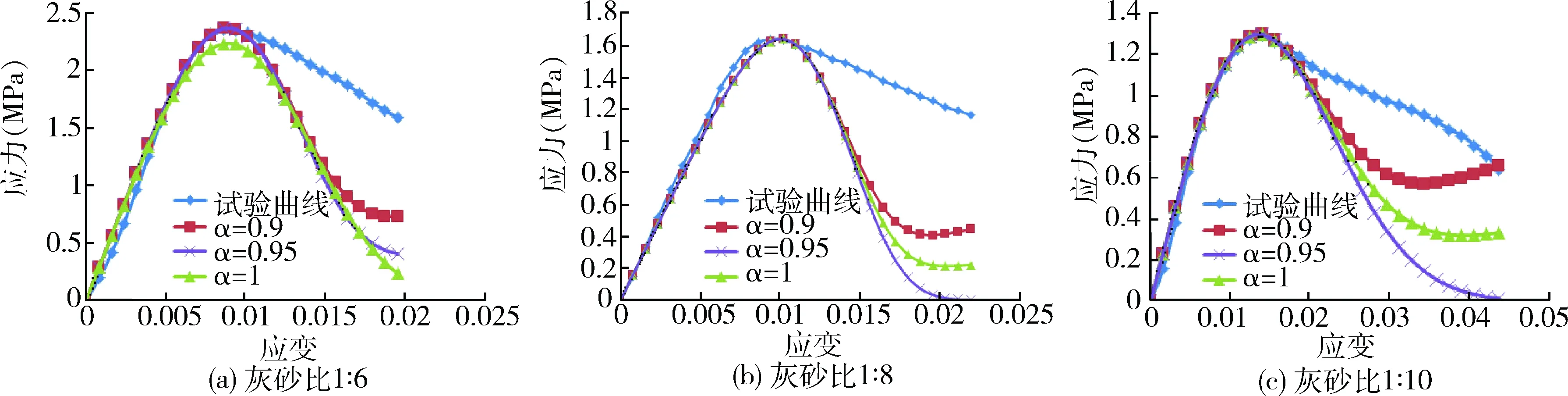
图2 单轴压缩试验曲线与理论曲线

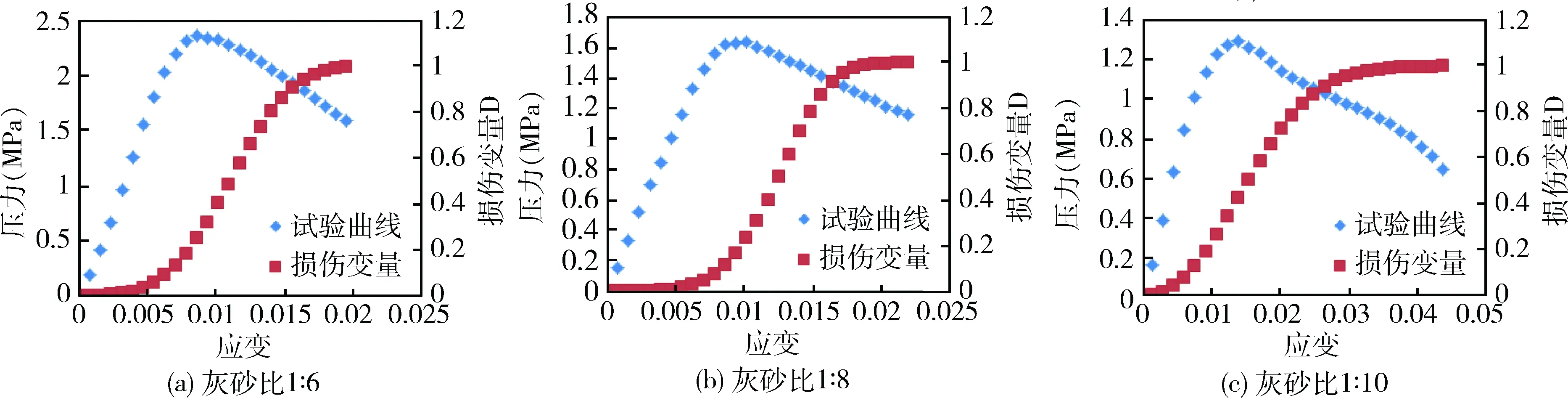
图3 充填体全过程曲线与损伤发展关系

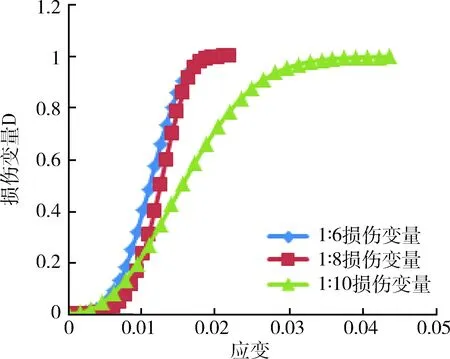
图4 不同灰砂比的充填体损伤发展曲线

由图3～4可知不同灰砂比的试件具有相似又相互区别的损伤演化规律。

1)不同灰砂比的充填体试件损伤发展趋势相同，均呈近似于S型增长。随着轴向应力与应变的不断增长，充填体损伤量逐渐趋近于1，此时充填体试件发生宏观破坏。

2)不考虑试件的初始损伤，在压密阶段可认为充填体损伤为0，试件以无损状态进入弹性变形阶段。以图3(a)为例，当应变为5.47×10-3时，充填体变形处于弹性变形阶段末期，损伤量仅为5.55%，损伤发展很小，可认为弹性阶段未发生损伤扩展。

3)从屈服强度至残破裂后阶段前期，充填体损伤发展迅速，其数值可占完全损伤值的75%以上。破裂后阶段末期，累计损伤量接近饱和，呈缓慢增长趋势，同时充填体强度也进入相对稳定期。

4)图4中灰砂比小的试件在相同变形的条件下具有相对较小的损伤值。本文重点探讨峰后强度阶段的损伤特点，以应变等于1.6×10-2时，此应变下三种试件均已破裂，各试件损伤值分别为0.92、0.88、0.51(按灰砂比由小到大)。表明灰砂比越小的充填体可承受更大的损伤，很好的发挥峰后承载能力。

4.2 Weibull参数m、F0对充填体全曲线的影响

充填体修正的统计损伤本构模型中参数F0和m反应了充填体变形的力学特性。由于在不同损伤率α时，曲线变形特点具有相似性，仅以α=0.9时为例探讨统计参数F0和m对损伤模型的影响，见图5～6。

图5 充填体变形全曲线与m关系

图6 充填体变形全曲线与F0关系

1)充填体应力-应变全曲线峰值随F0和m的增大而增大，但F0和m并不影响屈服前线弹性变形阶段曲线。

2)随着F0的增大，充填体应力-应变全过程曲线峰值强增大，同时峰值点右移，对于峰后阶段曲线斜率并未有显著影响。表明F0只是增加了屈服点以后的应力大小，未改变曲线的缓陡形态，各曲线具有相似性。

3)随着m的增大，充填体应力-应变全过程曲线峰值强度增大，但并未改变峰值强度所对应的应变。m改变了应力-应变全曲线的缓陡形态，随m的增大，曲线形态越陡，其所对应的残余强度越低。m值主要影响充填体峰后曲线残余强度的变化。

5 结论

1)对不同灰砂比的充填体进行单轴抗压试验，对比分析了不同灰砂比的充填体变形破坏规律，充填体变形可分为微孔隙压密、线弹性变形、非稳定破裂发展和破裂后阶段。灰砂比大的充填体具有更高的弹性模量、峰值强度和峰后残余强度。

2)在胶结充填体微元破坏概率服从Weibull分布的基础上，建立充填体统计损伤变量。为描述充填体破裂后阶段力学特征，引入α对损伤变量进行修正，得到了基于Weibull分布的修正的充填体损伤本构模型，并推导出Weibull分布参数F0，m数学表达式。

3)充填体损伤本构模型可以很好的描述充填体单轴压缩条件下的全过程曲线，尤其是峰后残余强度特征。修正损伤系数α主要表征了应力-应变全曲线峰后强度，α越小，充填体的峰后残余强度越高。Weibull统计参数F0和m主要表征充填体破坏曲线峰后阶段变形特性，F0和m越大，充填体峰值强度越大。修正损伤系数以及Weibull统计参数对屈服前阶段曲线影响很小。

4)不同灰砂比的充填体具有相似又相互区别的损伤演化规律。其损伤发展均呈近似于S型增长方式。在应变同为1.6×10-2时，1∶6灰砂比的充填体损伤值达到了0.92，而1∶10灰砂比的充填体损伤值0.51，说明低灰砂比充填体能够承受更大的变形，更好的发挥其承载能力。

[1] 于润沧. 我国胶结充填工艺发展的技术创新[J]. 中国矿山工程, 2010(5): 1-3.

[2] 谢和平, 岩石混凝土损伤力学[M]. 北京: 中国矿业大学出版社, 1990.

[3] 张淑坤, 王宾辉, 李伟, 等. 高速公路下伏采空区充填治理研究[J]. 硅酸盐通报, 2015, 34(4): 1485-1490.

[4] 饶运章, 舒太镜, 郑长龙, 等. 会宝岭铁矿全尾砂胶结充填最优配比试验研究[J]. 中国矿业, 2014, 23(3):97-100.

[5] 魏微, 高谦. 改进的BP神经网络模型预测充填体强度[J]. 哈尔滨工业大学学报, 2013, 45(6): 90-95.

[6] 付建新, 杜翠凤, 宋卫东. 全尾砂胶结充填体的强度敏感性及破坏机制[J]. 北京科技大学学报, 2014, 36(9): 1149-1157.

[7] 刘志祥, 刘青灵, 党文刚. 尾砂胶结充填体损伤软-硬化本构模型[J]. 山东科技大学学报: 自然科学版, 2012, 31(2):36-41.

[8] 张月征, 纪洪广, 侯昭飞. 基于莫尔-库仑强度理论的岩石冲击危险性判据[J].金属矿山, 2014(11):138-142.

[9] 曹瑞琅, 贺少辉, 韦京, 等. 基于残余强度修正的岩石损伤软化统计模型研究[J]. 岩土力学, 2013, 34(6): 1652-1661.

[10] 孙闯, 张向东, 李永靖. 深部软弱岩体峰后等效力学模型及数值计算研究[J]. 岩土工程学报, 2014, 36(6):1113-1121.

[11] 卢高明, 李元辉, 张希巍, 等.脆性岩石循环加卸载试验及应变损伤参数分析[J]. 金属矿山, 2015(5):28-33.

[12] 傅强, 谢友均, 龙广成, 等. 橡胶集料自密实混凝土的统计损伤本构关系[J]. 四川大学学报: 工程科学版, 2014, 46(4): 53-60.

[13] 杜修力, 金浏. 混凝土材料细观单元弹模非均质统计特性研究[J]. 工程力学, 2012, 29(10): 106-115.

[14] Kachanov L M, On the time to failure under creep condition[J]. Izv. Akad. Nauk. USSR. Otd. Tekhn. Nauk. 1958, 8: 26-31.

[15] 余寿文, 冯西桥. 损伤力学[M]. 北京: 清华大学出版社, 1997.

[16] Lemaitre J. Evaluation of dissipation and damage in metals submitted to dynamic loading[J]. Proceedings of ICM1, Kyoto, 1971.

[17] 王明超, 张佐光, 孙志杰, 等. 玄武岩纤维丝束强度的Weibull和Gauss分布统计分析[J]. 复合材料学报, 2008, 25(3): 105-109.

[18] 曹瑞琅, 贺少辉, 韦京, 等 基于残余强度修正的岩石损伤软化统计本构模型研究[J]. 岩土力学,2013, 34(6):1652-1667.

Study on damage model of backfill based on Weibull distribution under uniaxial compression

ZHAO Shuguo1,2, SU Dongliang1,2, WU Wenrui1, ZHANG Yalun1

(1.College of Mining Engineering, North China University of Science and Technology, Tangshan 063009, China; 2. Hebei Province Key Laboratory of Mining Development and Safety Technique, Tangshan 063009, China)

The deformation of backfill is mostly in the post-peak deformation stage in the actual stress environment of the mine. It is important to study the post-peak strength characteristics of backfill. Uniaxial compression test of backfill with cement-sand ratio of 1∶6, 1∶8 and 1∶10 were conducted. The deformation and failure characteristics of cemented backfill with different ratios were analyzed, the higher cement-sand ratio of the backfill, the higher peak strength and residual strength. Based on statistical damage theory, a damage variable of backfill is established. A new damage constitutive model which can simulate the full deformation process of backfill is established by modifying the damage variable. All these model parameters analytic solutions are deduced by the geometric features of uniaxial compression test curve. The smaller the α, the higher the residual strength of backfill, the greater the F0 and m, the greater the peak strength of backfill. The different cement-sand ratio of damage evolution are analyzed, different cement-sand ratio of backfill damage in an S-sharped growth model and low cement-sand ratio of backfill can withstand greater deformation, and better play to its bearing capacity. The result shows that, this model can describe the characteristics of the complete stress-strain curve and the post peak residual strength of cemented backfill very well, and provide reference for the design of backfill.

cemented backfill; Weibull distribution; Drucker-Prager criterion; residual strength; damage variable

2016-07-10

河北省自然科学基金项目资助(编号：E2015209172)；唐山市科技计划项目资助(编号：12140208A-12，12140208A-11)

赵树果(1969-)，女，河北尚义人，博士，教授，硕士生导师，主要从事矿山开采技术和安全技术及工程方面的研究工作,E-mail:157896200@qq.com。

TD853.34

A

1004-4051(2017)02-0106-06