基于物理场论的探测复杂网络社团结构的分布估计算法*

刘晋霞 孙丽萍 杜 静 刘晋钢 张 丽

(1.太原科技大学经济与管理学院，太原，030024； 2.山西省眼科医院，太原，030002； 3.太原工业学院计算机工程系，太原，030008)

基于物理场论的探测复杂网络社团结构的分布估计算法*

刘晋霞1孙丽萍2杜 静1刘晋钢3张 丽1

(1.太原科技大学经济与管理学院，太原，030024； 2.山西省眼科医院，太原，030002； 3.太原工业学院计算机工程系，太原，030008)

探测社团结构是复杂网络分析中一个基本和重要的问题。为提高探测社团结构的效率，本文提出了基于复杂网络场论的社团结构分布估计算法。通过设置不同种群规模，本文算法运用经典物理场论理论构建节点间场论模型，并在此基础上建立了社团结构概率模型，按照社团结构概率模型建立了分布估计算法。将该算法与GN(Girvan Newman)算法、遗传算法及启发式算法比较其产生的最优解，并分析它们的均值及方差的差异。结果表明：基于复杂网络场论的社团结构分布估计算法收敛速度较快，划分效果较好。

社团结构;复杂网络;分布估计算法;场论

引 言

社团结构是反映复杂网络整体结构性质的重要特征[1]，深入分析社团结构，可系统地把握实际复杂网络的结构关系及特性[2]。在社团结构探测方法研究中，GN算法为早期较经典的算法，其突出贡献在于引入了最大边介数和模块度Q指标，尤其是模块度指标已成为衡量社团划分优劣的指标[3]。之后Newman又提出了一种贪婪算法[4]，改分裂方法为聚合方法。Clauset等采用堆结构的方法改进了贪婪算法，即CMM算法[5]。在借鉴和继承GN算法思想的同时，还提出了极值优化方法[6]、信息中心度法[7]和层次聚类法[8]等。这些方法的共同点是以模块度作为判断社团结构划分优劣的标准，同时引入了在分裂或聚合时所用的中间变量[9]。目前社团结构探测算法数以万计，可分析归纳为3类：(1)通过矩阵的视角去分析研究，即通过构建邻接矩阵反映节点间的连接关系，以此为基础分析其特征值，利用矩阵特征值的谱提出社团划分的方法[10]；(2)通过社团结构形成机理去分析其结构，如随机行走法[11]和Potts模型算法[12]；(3)基于优化方法的社团结构探测方法，在优化方法中分别以模块度、模块密度和社团度等指标作为优化函数进行社团结构探测[13-14]。经典的优化方法[15]有线性规划法、整数规划法、分枝定界法和动态规划法等[16-17]。

遗传算法采用“构造块假设理论”和“模式定理”，通过交叉和变异实现组合优化，但在迭代进化过程中实现的交叉和变异的概率随机重组会破坏构造块，出现算法退化现象，导致算法早熟收敛或陷入局部最优[18]。分布估计算法 ( Estimation of distribution algorithms， EDA)[19]是以遗传算法为基础的进化算法[20]，但又与遗传算法不同，它舍弃了交叉和变异算子，根据当前种群的概率分布产生下一代种群，重复这个过程直到满足结束条件[21]。该算法结合了进化计算和统计学习两个领域的知识，其概念源起于Ackley1987年提出的“基因向量”的重要概念，1996年由Mühlenbein提出分布估计算法，目前其已在进化计算领域占有一席之地[22]。分布估计算法的核心是建立一个能恰当描述问题解分布的概率模型，根据变量的连续与否，又可将分布估计算法分为离散域分布估计算法和连续域分布估计算法[23]。用分布估计算法解决社团结构探测问题，首先是对问题界定：从变量的定义域看，对给定节点进行社团划分，不研究社团结构随时间的变化，故属于离散问题；从优化对象看，是通过寻找离散事件的最优组合，故复杂网络社团结构探测是对离散的组合优化问题求解。针对离散的组合优化问题，其关键是能构建合适的概率模型，准确反映解空间的分布。目前已有的分布估计算法研究离散问题多应用于求解背包问题[24]、输电网扩展规划[25]、最小化图转换问题[26]和生产调度问题[27]等，尚未应用于复杂网络的社团结构探测[28]。分布估计算法最初假定变量间相互独立，不考虑变量间的相关性[29]，而用分布估计算法对复杂网络进行社团结构探测，不仅要考虑两两相关，还要考虑节点分配至不同社团对其相邻节点的影响。

本文基于经典物理学的场论理论，通过研究复杂网络中节点之间的作用关系，分析一个实体与其他实体之间的作用力，以场论的视角，视复杂网络各节点的度为质量，利用节点的连接为线性空间的度量空间，从而构造出基于复杂网络场论的社团结构概率模型。以该概率模型为基础设计了社团结构分布估计算法，既考虑了节点间的两两相关性，也兼顾了节点分配至不同社团对其相邻节点的影响。

1 构造复杂网络场论模型

场论是经典物理学的重要组成部分，分为自然场和社会场。其中，自然场有引力场、温度场和电磁场等；而社会场是把社会当作一个场，其中也有类似磁场的一些性质，具有相互影响的能量[30]。在场中，一个个体对其他个体产生的影响可用作用力表示，它的作用范围仅限于处于该场域范围内的其他个体，作用力的实质是个体间质能关系的反映[31]。场力的统一公式为

(1)

式中：M为物质本身的性质，如质量、温度和重要性等；r为两物质之间的距离，如客观距离、关系等；K为作用力系数。作用力正比于自身物质性质的场力，反比于距离的平方。

1.1 节点的物质性和节点间的距离

复杂网络中的节点是个体的抽象，从自然场论角度出发，节点的物质性即它的度，只有度值能反映出类似质量的性质，体现其在复杂网络中的势能或重要性，故用节点度值作为节点的物质性M。对于任意节点a，则有

Ma=Degree(a)

(2)

客观世界的距离可用三维空间的距离公式表示两点距离，而在复杂网络中节点间的距离可理解为是否有边相连，当两点间有边连接时，认为节点间距离为1，否则认为是∞。

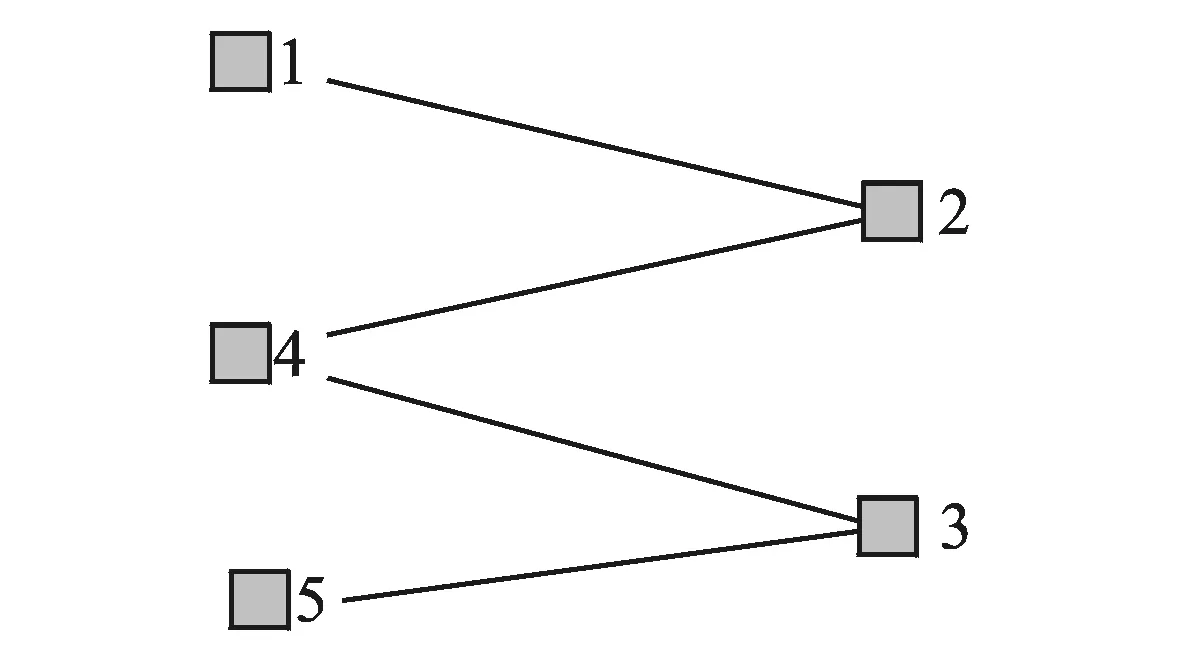
图1 5节点网络距离关系示意图Fig．1 Distance relationship sche-me of 5 node network

如图1所示，对于任意5个节点之间的连接,其邻接矩阵为A，则任意两点之间的距离为

(3)

节点1到节点2之间有连边，故r1→2=1，而节点1到节点3之间没有连边，则r1→3=∞。A可以表示为

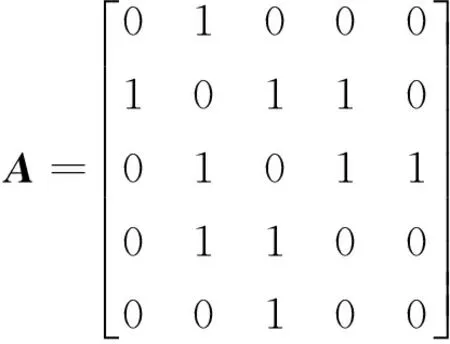
(4)

1.2 引力系数

社团结构通常采用基于相对连接频数的定义：网络中的顶点可以分成组，组内连接稠密，而组间连接稀疏[32]。在自然科学发展历史上，人们习惯于将一些量称为常数，其中当然就包括引力系数和普朗克数，但引力系数不是恒定的。例如重力加速度约定为g=9.80665 m/s2，是在纬度45°时重力为1千克力，而在赤道和两极上称得的重量分别是0.973千克力和1.26千克力。故引力系数是可变的。

针对复杂网络社团结构探测问题，以节点的度值作为节点的物质性，两节点的度值无论是多少，它们的连边仅占两节点度值之和减1分之一，故定义引力系数k为

(5)

式中：Ma，Mb分别为节点a和节点b的度，也可理解为节点a和节点b的所有度，即两节点度之和减1，当节点a和节点b之间仅一条连边且不与其他节点相连时，k值为1。

把复杂网络节点间的分布看作场，从节点间作用力的角度出发，构造出节点间的场论模型，然后基于复杂网络场论模型，可进一步建立相应的概率模型。

2 基于复杂网络场论的社团结构概率模型

无论是社团结构优化函数还是社团结构定义，其核心判断标准都是节点间连接的紧密程度，而复杂网络场论模型可反映节点间作用力关系，在此基础上构建社团结构概率矩阵。社团结构概率矩阵依据复杂网络中任意两节点之间的作用力大小建立，故首先构造节点间作用力矩阵。

图2 具有社团结构的小网络图Fig．2 Small network with community structure

2.1 节点间作用力矩阵

不同的节点由于自身的度值，通过连边对其他节点形成了场效应。如两节点之间有边相连，那么其中一节点a对另一节点b的物质场作用力等价于节点b对节点a的物质场作用力[33-34]，其表达式为

(6)

对于一个有两个社团结构的小复杂网络，如图2所示。对节点8和节点11的作用力关系，有

(7)

故作用力矩阵F为

(8)

2.2 社团结构概率模型

节点间作用力矩阵仅反映两节点之间有连边情况下的作用力关系，体现不出无直接连边的两节点的关系。通过节点间作用力关系，可进一步导出社团结构概率矩阵C。

(9)

由作用力矩阵知，当节点i,j之间有连边时对应的作用力矩阵fij不为0。如图2所示，节点1和节点5之间有连边，f15=1，而通过节点5，节点1的场力还可以作用于节点4和节点6。将作用力分成两类来计算：直接作用力和间接作用力。

(10)

对于间接作用力产生的吸引作用，如节点6和节点7的吸引力关系，先找到与节点6相连且与节点7相连的节点：节点2和节点8，将作用力相乘f62×f27,f68×f87并求和，再分别与节点6的作用力之和、节点7的作用力之和比较求均值，即可得节点6和节点7的吸引力关系。对于图2所示14个节点的复杂网络，其社团结构概率模型为

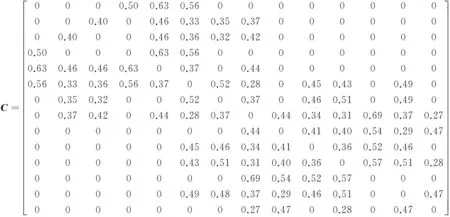
(11)

由式(11)可看出各节点可能同属于一个社团的概率，如节点1和节点4，5，6的概率超过半数，和其他节点同属一个社团的概率为0。该概率模型只能横向或纵向比较，交叉比较无意义。如节点2与节点3，同在一个社团的概率为0.40，而节点13与节点7，同在一个社团的概率为0.49，这个比较毫无意义。

3 基于复杂网络场论的EDA算法

根据复杂网络场论模型可得有连接节点间作用力关系，从而求得社团结构概率模型C。基于复杂网络场论的EDA算法首先从种群中选择优势群体，构建社团结构概率矩阵，依据概率矩阵反复抽样，从而产生新的优势群体，依据作用力关系建立新的社团结构概率矩阵，采用上述方式，反复抽样，当划分结果在若干代内保持不变时，优化过程结束。

算法基本流程如下：

(1) 初始化种群，随机产生M个个体。

(2) 以社团度指标C作为适应度函数，计算每个个体的适应值，当最大适应度值连续k代保持不变可跳转执行(5)。

(3) 根据适应度函数的值，建立作用力矩阵及社团结构概率模型。

(4) 从社团结构概率矩阵中抽样产生新群体，从新个体和旧个体中分别选出一定数量的最优个体，作为下一代优势群体，跳转至(2)。

(5) 输出最优划分社团。

执行上述流程，当最大适应值或社团结构划分结果在连续几代不变时，输出最优结果。为保证算法的收敛效果，采用最优保留策略。

3.1 分布估计算法仿真实验流程

为验证本文所提出的基于复杂网络场论的社团结构分布估计算法的可行性，以有社团结构的图2为例，该图有两个明显的社团结构，有14个节点。初始群体为x0，群体规模为5，目标是划分成2个社团，以此进行仿真测试及解析。主要优化步骤为

步骤1 初始化：将14个节点随机划分成两个社团，生成5个个体，组成初始解群体。

步骤2 适应度计算：以社团度指标C作为适应度函数，计算每个个体适应度值，并以此排序。当最大适应度值连续k代保持不变可跳出循环。

(12)

步骤3 建立作用力矩阵及社团结构概率模型：建立节点间作用力矩阵，构建两节点之间作用力关系F，以此关系为基础，构建社团结构概率矩阵C，如式(8，11)所示。

步骤4 从社团结构概率矩阵中抽样，产生新群体：设定参数δ=0.5，当Cij≥δ时，认定为同一社团，否则属于另一社团。计算新个体适应度值，从新个体和旧个体中选出5个最优个体，作为下一代优势群体。跳转至步骤2，当最优个体在连续k代保持不变时，执行下一步，否则跳转至步骤5。

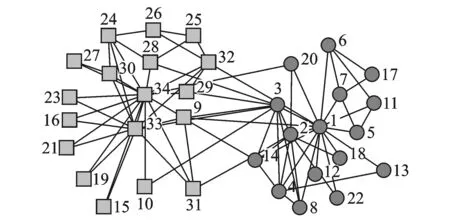
图3 Zachary成员划分Fig．3 Partition of Zachary network

步骤5 输出最优划分社团。

3.2 Zachary空手道俱乐部实验结果

Zachary网络是一经典的社会网络，是Zachary观察构造的，它由34个节点和78条边组成[35]，描述了空手道俱乐部成员间关系[36]。用基于复杂网络场论的EDA算法将该网络划分为两个社团，如图3所示。

3.3 仿真实验分析

以Zachary网络划分为例，将基于场论的EDA算法与GN算法[37]、遗传算法[38]和启发式算法[39]作比较，以社团度指标C为优化变量，设种群规模N分别为5，10，20，以20次实验为一单元，比较其平均收敛代数、正确划分次数及C的平均值。

Zachary网络划分的实验结果如表1所示。从表1可看出，各算法均能找到最优解，种群规模小的，平均迭代次数大，分布估计算法的平均收敛代数略低于其他算法，且C的平均值高于其他算法，说明在相同种群规模条件下，分布估计算法的收敛速度较快，优化性能略优。

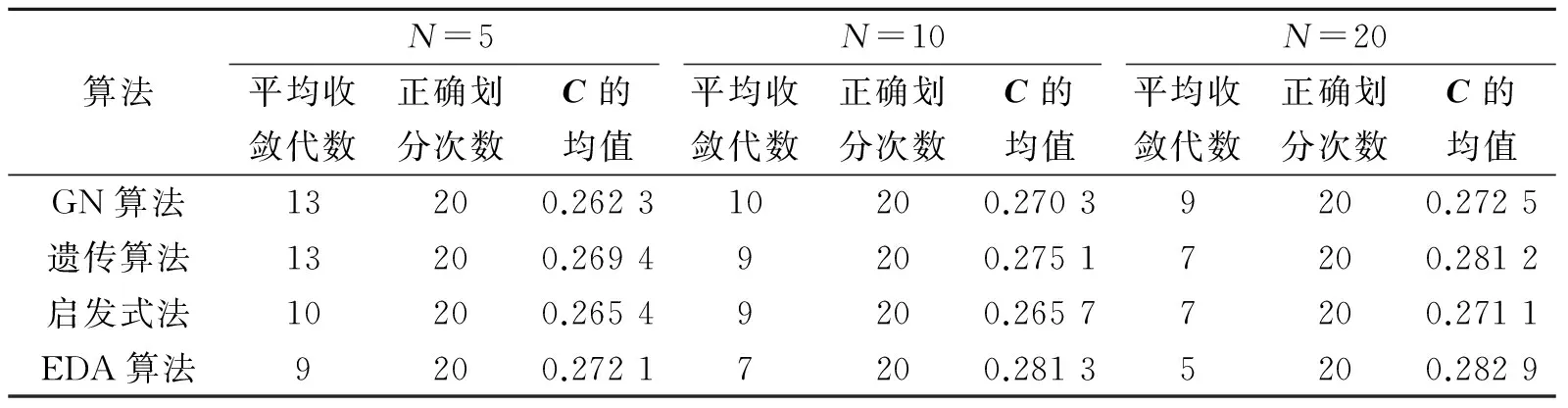
表1 Zachary网络划分运行结果

4 结束语

社团结构探测多是通过优化的方法去探测，很少去分析各变量之间的内在关系。本文以复杂网络场论为基础，基于节点间作用力关系，通过更新社团结构概率矩阵，提出基于复杂网络场论的分布估计算法。以Zachary网络为例，比较各算法的平均收敛代数、算法正确率及C的平均值，通过实验数据可看出基于场论的分布估计算法收敛速度快，在不同的种群规模条件下，种群规模小时，平均收敛代数多，种群规模大时，平均收敛代数少，而C的均值差值小。在相同种群规模条件下，分布估计算法的收敛速度较快，优化性能略优。但对于算法收敛速度快，是否会限入局部最优等问题，还需要在算法的收敛性证明方面做进一步的论证工作及更多的补充实验。

[1] Barabási A L, Albert R, Jeong H. Mean-field theory for scale-free random networks[J]. Physical A, 1999, 272(1/2): 173-187.

[2] Star X Zhao, Fred Y Ye. Exploring the directed h-degree in directed weighted networks[J]. Journal of Informetrics, 2012, 6(4): 619-630.

[3] Wang W Q, Zhang Q M, Zhou T. Evaluating network models: A likelihood analysis[J]. Europhysics Letters, 2012, 98(2): 28004.

[4] Girvan M, Newman M E J. Community structure in social and biological networks[J]. PNAS, 2002, 99: 7821-7826.

[5] Newman M E J， Girvan M. Finding and evaluating community structure in networks[J]. Phys Rev E，2004,69 (2): 026113.

[6] Clauset A， Newman M E J， Moore C. Finding community structure in very large networks[J]. Phys Rev E，2004，70: 066111.

[7] 黄晓可, 刘洛琨, 郭虹. 一种基于短LT码的级联编译码算法[J]. 数据采集与处理, 2014,29(3):445-450.

Huang Xiaoke, Liu Luokun, Guo Hong. A concatenated coding algorithm based on LT codes with small message length[J]. Journal of Data Acquisition and Processing, 2014,29(3):445-450.

[8] Strogatz S H. Exploring complex networks[J]. Nature, 2001,410(6825): 268-276.

[9] Hu Y， Nie Y， Yang H， et al. Measuring the significance of community structure in complex networks[J]. Phys Rev E, 2013, 82: 066106.

[10]Lee S, Yook S H, Kim Y, et al. Centrality measure of complex networks using biased random walks[J]. EPJB, 2009, 68(2):277-281.

[11]Liu Jinxia, Zeng Jianchao. An improved genetic algorithm optimizing the quantitative function of communicability to detect community structure[J]. ICIC Express Letter, 2012, 6(7): 32-37.

[12]Holland P W， Laskey K B， Leinhard S. Stochastic blockmodels: First steps[J]. Social Networks, 1983, 5: 109-137.

[13]刘晋霞，曾建潮，薛耀文. 用遗传算法优化模块密度探测社团结构[J]. 解放军理工大学学报，2011, 32(3):386-390.

Liu Jinxia, Zeng Jianchao, Xue Yaowen. Genetic algorithm optimizing modularity density for community detection[J]. Journal of PLA University of Science and Technology, 2011, 32(3):386-390.

[14]Li Z P, Zhang S H, Wang R S, et al. Quantative function for community detection[J]. Phy Rev E, 2008, 77(3): 036109.

[15]Newman M E J. Fast algorithm for detecting community structure in networks[J]. Phys Rev E, 2004,69(6):061901.

[16]Anderson E J. Philpott. A continuous-time network simplex algorithm[J]. Networks, 1989, 19 :395-425.

[17]He X J, Zeng J C, Xue S D, et al. An efficient estimation of distribution algorithm for job shop scheduling problem[J]. Swarm, Evolutionary and Memetic Computing Lecture Notes in Computer Science, 2010,6466(8): 656-663.

[18]Chen D, Lü L, Shang M S, et al. Identifying influential nodes in complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2012, 391(4):1777-1787.

[19]Ma X K, Gao L, Yong X R, et.al. Semi-supervised clustering algorithm for community structure detection in complex networks[J]. Physica A, 2010, 389(12): 187-197.

[20]Holland J H. Adaptation in natural and artificial systems[M]. Cambridge: MIT Press, 1975:31-45.

[21]Larranaga P, Lozano J. Estimation of distribution algorithms: A new tool for evolutionary computation[M]. Norwell: Kluwer Academic Publishers, 2002.

[22]Lü L, Pan L, Zhou T, et al. Toward link predictability of complex networks[J]. PNAS, 2015, 112(8): 2325-2330.

[23]Pelikan M, Goldberg D E, Lobo F. A survey of optimization by building and using probabilistic models[R]. ILLiGAL Report No. 99018. Urbana: University of I11inois at Urbana-Champaign, I11inois, 1999.

[24]何晓娟. 分布估计算法及其在生产调度问题中的应用研究[D]. 兰州: 兰州理工大学, 2011.

He Xiaojuan. Estimation of distribution algorithm and it′s application in scheduling problems[D]. Lanzhou: Lanzhou University of Technology, 2011.

[25]何建军. 复杂网络节点重要性评价研究[D]. 长沙：湖南大学, 2010.

He Jianjun. Evaluation node importance in complex networks[D]: Changsha: Hunan University, 2010.

[26]Paul T K, Iba Hitoshi. Linear and combinatorial optimizations by estimation of distribution algorithms[C]∥Proceedings 9th MPS Symposium on Evolutionary Computation. IPSJ, Japan:[s.n.], 2002: 1-8.

[27]John McCall. Genetic algorithms for modelling and optimization[J]. Journal of Computational and Applied Mathematics, 2005, 184 (1): 205-222.

[28]Fortunato S, Barthelemy M. Resolution limit in community detection[J]. PNAS, 2007, 104(1): 36-41.

[29]Chen Hongbin, Hu Yanqing, Di Zengru. Community detection with cellular automata[J]. Journal of Beijing Normal University: Natural Science, 2008, 44(2):153-156.

[30]Alguaci N， Motto A L， Conejo A J. Transmission expansion planning: A mixed-integer LP approach[J]. IEEE Trans on Power Systems, 2003, 18(3) :1070-1077.

[31]Dogan A. Probabilistic approach in path planning for UAVs[J]. IEEE International Symposium on Intelligent Control. 2003，1(6):608-613.

[32]Yang S, Wang D. A new adaptive neural network and heuristics hybrid approach for job-shop scheduling[J]. Computers Operations Research, 2001, 28(10):955-971.

[33]Benson R1. Review: Field theory in comparative context: A new paradigm for media studies[J]. Theory and Society, 1999, 28(3):4632-4981.

[34]张敏灵. 偏标记学习研究综述[J]. 数据采集与处理， 2015,30(1):77-87.

Zhang Minling. Research on partial label learning[J]. Journal of Data Acquisition and Processing, 2015, 30(1):77-87.

[35]Zhou T, Liu J G, Bai W J, et al. Behaviors of susceptible-infected epidemics on scale-free networks with identical infectivity[J]. Physical Review E, 2006, 74 (5): 056109-056120.

[36]Zachary W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research， 1977, 33(4):452-473.

[37]Liu Jinxia, Chao Zengjian, Xue Yaowen.Quantitative function for community detection[C]∥ICEEAC The International Conference on Electrical Engineering and Automatic Control 2010. Zibo, China: Shandong Institute of Automation, 2010:V2-261.

[38]刘晋霞，曾建潮，薛耀文.复杂网络强社团结构探测[J]. 小型微型计算机系统， 2011, 32(4):686-690.

Liu Jinxia, Zeng Jianchao, Xue Yaowen. Basing on strong definition of community detect community structure in complex networks[J]. Journal of Chinese Computer Systems, 2011, 32(4):686-690.

[39]Zhou Haijun. Distance, dissimilarity index, and network community structure[J]. Physical Review E, 2003, 67(6):061901-10.

Estimation of Distribution Algorithm for Detecting Community Structure of Complex Networks Based on Field Theory Model

Liu Jinxia1, Sun Liping2, Du Jing1, Liu Jingang3, Zhang Li1

(1.College of Economics and Management, Taiyuan University of Science and Technology, Taiyuan, 030024, China; 2.Shanxi Eye Hospital， Taiyuan， 030002， China; 3.Department of Computer Engineering, Taiyuan Institute of Technology， Taiyuan， 030008， China)

Identification and detection of the community structure is fundamental and important in the analysis of complex network. To detect community structure precisely, a new community detection algorithm based on EDA (Estimation of distribution algorithms) and field theory is proposed. By studying the instance relation of complex network and introducing the field theory, a community structure probability model is built. The proposed algorithm is illustrated and compared with GN (Girvan Newman) algorithm, genetic algorithm and heuristic algorithm by using classic real world networks. The result demonstrates the proposed algorithm is converge quickly and good practice.

community structure; complex network; estimation of distribution algorithms; field theory

国家自然科学基金(71273159，71503108)资助项目；太原市软科学(W2012036)资助项目；博士科研启动项目(W20142003)资助项目。

2015-05-10；

2015-06-15

N94;TP301.6

A

刘晋霞(1973-)，女，副教授，研究方向：复杂网络，智能算法，E-mail:ljx2748@163.com。

孙丽萍(1979-)，女，硕士研究生，研究方向：公共卫生管理，E-mail:slp2046@126.com。

杜静(1974-)女，讲师，研究方向：电子商务安全，人工智能，E-mail:7426915@qq.com。