基于网格搜索与交叉验证的SVM磨机负荷预测

罗小燕，陈慧明，卢小江，熊 洋

（江西理工大学机电工程学院，江西 赣州 341000）

基于网格搜索与交叉验证的SVM磨机负荷预测

罗小燕，陈慧明，卢小江，熊 洋

（江西理工大学机电工程学院，江西 赣州 341000）

针对实际生产中只能依据专家经验判断磨机负荷（ML）状态，难以检测ML及其直接相关参数的问题，该文通过分析反应磨机内部负荷的振动信号，提取频谱特征，利用支持向量机（SVM）建立磨机负荷参数的预测模型。为解决SVM核函数参数g和惩罚因子C主观选取问题，提出采用网格搜索与交叉验证相结合的方法，对SVM参数进行优化。最后基于Matlab与VC混合编程，建立仿真平台，实现球磨机负荷参数的预测仿真。分别利用SVM默认参数和最佳优化参数代入ML回归预测模型，通过参数ML预测对比，得到SVM最佳优化参数下训练的平均平方误差（MSE）和平方相关系数（r2）均优于SVM默认参数下的预测结果。

磨机负荷；网格搜索；交叉验证；参数优化；混合编程

0 引 言

磨矿是选矿生产流程中十分重要的环节[1]，它是将矿石碎磨至使有用矿物基本单体解离或富集合的细度，再经过分级过程后供浮选，磨矿工序产品质量的好坏直接关系着整个选厂的经济和技术指标。磨矿过程是选矿生产中的耗能大户，通常该工序成本占总生产费用的40%～60%。因此，科学、准确地预测磨机内部运行状态及开发磨矿优化控制技术是选矿行业实现节能降耗、提质提产的根本任务之一[2]。

近年来基于支持向量机的磨机负荷软测量检测方法研究越来越多，取得了相应的成果。澳大利亚CSIRO公司开发了在线筒体振动检测系统，建立了支持向量机预测模型控制磨机运行状态，降低了钢耗[3]。文献[4]根据磨机负荷参数与筒体振动的相关性，建立基于支持向量机的磨机负荷参数软测量模型。基于主元分析（PCA）提取分频段特征，文献[5]提出建立支持向量机（SVM）模型预测磨机内部负荷的方法。文献[6]提出多源数据特征融合的球磨机负荷软测量，利用SVM建立磨机负荷模型。上述方法都是在利用SVM建模过程中，SVM参数都是根据经验选用定值，这样使模型的学习和泛化能力下降，导致模型的预测效果不理想。

为了使SVM更好地应用在工程实际中，文献[7]利用网络搜索对SVM参数进行优化，很好地解决了梯级水电系统隐随机调度问题。文献[8]利用最小二乘SVM参数优化模型在煤矿安全预测中应用，很好地解决了样本的高维、不确定性等方面的问题，文献[9]采用多种群混合算法进行SVM预测模型参数的优化选取，结果表明该方法能够满足球磨机负荷检测的实时性要求。基于此本文提出基于交叉验证与网格搜索对SVM进行参数寻优，利用优化模型对磨机内部负荷参数进行预测。

1 SVM基本原理

SVM对样本分类的方法是根据统计学的VC维理论和结构风险最小原理进行的，对特定训练样本的学习精度和学习能力之间寻求最佳折衷，以期获得最好的泛化能力[10]。SVM主要思想是建立一个超平面作为决策曲面，使得待分样本之间的间隔最大化，并实现将分类问题转化为一个带约束的最值问题，如下式：

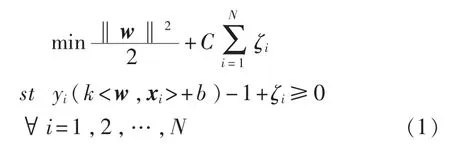
式中：ζ——松弛变量；

C——惩罚因子；

N——样本数。

由式（1）可知影响SVM模型精度主要有松弛变量ζ和惩罚因子C。其中松弛变量ζ使SVM在样本回归时，具有容错能力[11]；而惩罚因子C是解决SVM分类器为了少量离散点而使得目标‖w‖变小的问题[12]；核函数k＜w，xi＞反应了各支持向量的相关程度，将向量w与xi在低维空间不可分的情形映射到高维空间再进行内积，实现将模型的求解转换为带约束的规划问题。常用的核函数如表1所示。

表1 常用核函数

2 SVM模型参数优化

根据SVM基本原理，核函数g和惩罚因子C对模型起着关键的作用，故本文利用网格搜索与交叉验证相结合的方法对参数g和C进行寻优。

2.1 交叉验证

交叉验证是在样本训练过程中消除随机取样所带来偏差的方法[13]，它的基本思想是，按照事先设定的规则将原始样本分为训练集和测试集。首先通过训练样本对模型进行训练，再用测试样本对训练得到的模型进行验证，以此评价模型的准确性。常用的交叉验证方法有K-fold交叉验证法、重复随机抽样法、留一法等。其中K-fold交叉验证法具有计算效率高的特点，故本文采用K-fold交叉验证法对训练得到的模型进行性能评价。K-fold法是将原始样本分成K组，将每个子集样本分别做一个测试集，其余K-1组样本作为训练集，得到K个模型，用这K个模型最终测试集的准确率的平均数作为此模型下的性能指标。

利用K-fold法对模型的训练样本性能进行评价，以模型准确率最高的SVM参数作为优化参数，提高了模型的稳定性和泛化能力。交叉过程中，各组参数下的模型准确率通常采用最小均方误差（MMSE）来表征，在参数空间内寻优，找到均方误差最小的参数取值。均方误差为

式中：yi——实际值；

2.2 网格搜索

网格搜索是一种穷举法，是指在参数空间每维上取若干分隔，计算时遍历参数空间所有网格交叉点得到最优解，其优点可以保证所得的最优解是划分网格中的全局最优解，避免了由于人为给定值所造成的重大误差。文中对C和g进行寻优，将网格在其各自区域等分为M和N个点，形成一个M×N的网格平面。在每个参数组合通过交叉验证的方法可计算出其估计模型的MMSE，当计算遍历网格平面的每个节点时，可找出MMSE最小的参数组合，即为最优参数。

2.3 参数选取步骤

网格搜索法可遍历每个可能的参数组合，结合交叉验证方法可找出使MMSE最小时的参数组合，从而避免了局部最优解的出现，本文在网格搜索中应用K-fold交叉验证法对每组（C，g）的性能指标进行评价。基于K-fold交叉验证的网格参数寻优步骤如下：

1）选择初始化参数选择范围。令a=[-a1，a2]、b= [-b1，b2]，步长为1，取网格参数的节点为C=2a、g=2b。

2）划分样本。将训练数据等分为K个子集，对网格中每一组参数（C，g），首先任意选择一个子集作为测试集，其余K-1个子集作为训练集，利用训练集训练模型后对K-1个测试集进行预测，统计该组参数下测试结果的均方误差值。

3）求取预测误差值。将下一组子集作为测试集，剩下的K-1个子集作为训练集，统计该组参数下测试结果的均方误差值，直至K个子集都被作为一次测试集后，取K组均方差的平均值δMMSE作为该组参数的预测误差。

4）求取最优的参数组合。更换参数组合（C，g），重复步骤2）、3），分别计算出网格中各参数组合下模型的均方差平均值δMMSE，并对其进行大小排序，选出δMMSE最小时对应的组合参数（C，g）即为网格区间内最优的参数组合。

利用K-fold方法，以参数平均误差δMMSE最小化为参数优选的目标，以各参数范围为约束条件，避免了训练样本的随机性对模型准确率的影响，提高了参数优选的效率和准确性。

3 磨机负荷预测仿真与结果分析

3.1 磨矿试验

采用型号为480mm×260mm的小型球磨机进行磨矿实验，球磨机转速为42 r/min，即筒体每转动一圈需0.7s，为使频谱分析结果能全面反应筒体整体情况，每个振动数据样本选取磨机运行的5个运转周期，共选5个数据样本，每个样本数据长度5 000×8。根据实际生产经验总结，在磨矿过程中选取转速率为0.8，填充率为20%，料球比分别为0.6，0.8，1.0，1.2进行磨矿试验，分别测取各自状态下的振动信号，试验方案如表2所示。磨机尺寸：480mm×260mm；转速率：0.8；入料粒度：1～9mm。

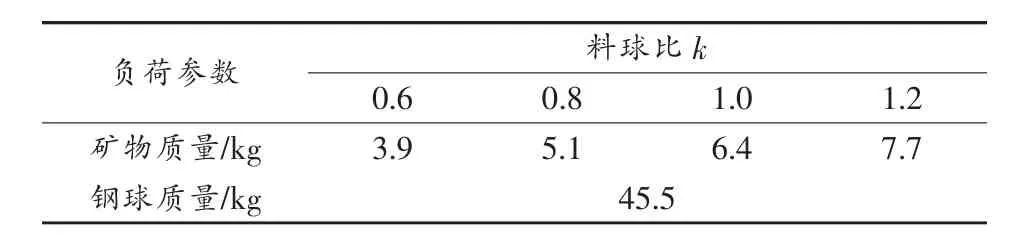
表2 负荷填充率为20%的矿物和钢球质量

试验步骤：

1）预先对待磨矿料进行筛分，入料粒度在1～9mm范围的矿料为实验所用矿料；

2）按照填充率、料球比计算好的钢球质量和物料质量给磨机填料，关闭进料口，调节变频器至计算值，启动球磨机，并开始计时；

3）清零和平衡动态数据采集仪，设定采样频率为5kHz，待磨机运行1 min后，开启数据采集仪，待磨机运转5个周期后，关闭数据采集仪，停止磨机；

4）为了保证实验条件一致性，取出矿物，重复步骤1）～3），得到不同运行状态参数下的振动信号，进行后续分析研究。

3.2 SVM参数优化

本文基于Matlab与VC混合编程技术，建立仿真平台，实现磨机内部负荷参数的预测仿真，仿真系统主要包括，系统模块、信号导入模块、信号分析和负荷预测模块。各模块具体内容如下：

信号导入模块：将振动数据样本导入，采用阈值小波去噪方法对振动信号进行去噪处理，为消除不同频谱段振动信号的幅值对预测结果的影响，统一将数据处理为区间[0，1]之间的数据，如下式：

xmin——总体数据中最小值；

xmax——总体数据中最大值；

x——当前值。

信号分析模块：对振动信号进行功率谱估计，根据振动信号的能量谱较高的频率段，提取反映磨机内部负荷的振动信号，得到振动信号的频谱特征。

负荷预测模块：基于网格搜索和交叉验证对SVM参数进行寻优，得到SVM模型最优化参数C和g，并将得到的最优参数输入到SVM负荷预测模型。仿真系统负荷参数预测过程如图1所示。

3.3 仿真结果分析

图1 负荷参数预测流程

基于VC和Matlab混合编程方法，是将SVM的模型训练和预测模块（.cpp文件），选择C++编译器将VC文件编译为Matlab可识别文件（.m），最后设置VC和Matlab对应的数据接口即可。利用建立的磨机负荷参数的预测仿真平台，磨矿过程在填充率为20%，料球比分别为0.6，0.8，1.0，1.2的磨矿负荷参数下，进行负荷参数的预测验证。SVM参数优化结果及对应的预测准确率，结果如图2所示。

图2 SVM参数选择3D结果图

从图中可以看出，当SVM核函数参数g和惩罚因子C不断变化过程中，球磨机负荷预测准确率也相应不断变化。采用网格搜索与交叉验证寻优得到，当惩罚因子C为0.57，核函数参数g为84.45时，磨机内部运行状态参数预测准确率最高，达到97.2%。

将寻优得到的磨机负荷最优参数组合（C，g）代入到SVM负荷预测模型，取振动数据样本400组为训练样本，另400组为测试样本，以平均平方误差MSE和平方相关系数r2作为评价指标，求得训练样本和测试样本的预测结果如图3所示。

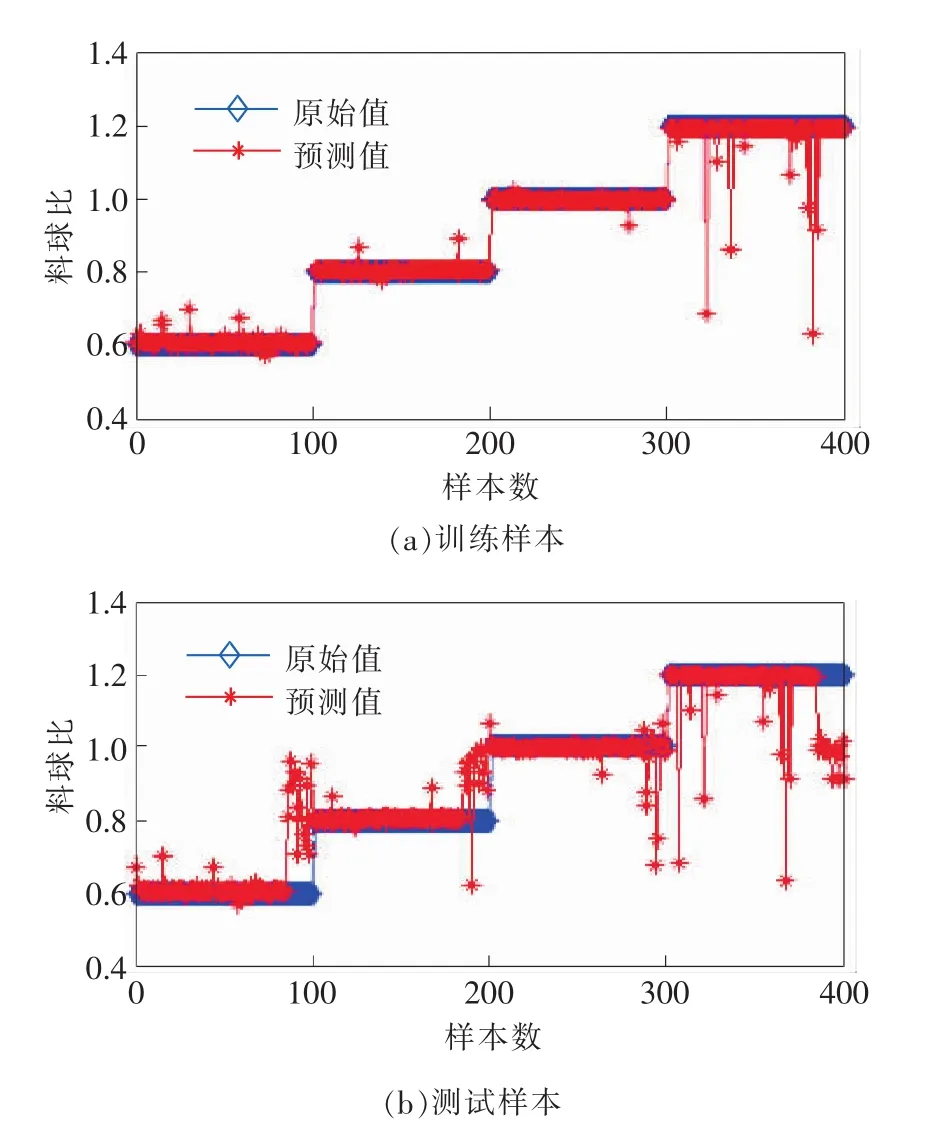
图3 训练样本和测试样本的预测结果图

由图3（a）训练样本预测误差较低，负荷参数料球比为1时，误差最小，而料球比增加到1.2时，预测误差增大，在测试样本预测结果有相类似的趋势；通过对比图3（a）、图3（b）发现料球比预测误差有向中趋势，即在料球比为1时预测误差最小。

分别利用SVM默认参数和最佳优化参数代入负荷回归预测模型，对上述数据样本进行预测，得到两种模型在训练和测试样本的平均平方误差MSE和平方相关系数r2，如表3所示。

表3 两种模型预测结果比较

从表3可以看出，K-SVM最佳优化参数下训练的平均平方误差MSE和平方相关系数r2分别为0.24和97.2，测试集分别为0.83和95.3，均优于SVM默认参数下的预测结果。

4 结束语

1）采用网格搜索与交叉验证相结合的方法，对SVM参数进行优化，避免了SVM核函数参数g和惩罚因子C主观选取问题，提高了模型的泛化能力，降低了模型预测误差，预测的准确率达到97.2%。

2）通过利用Matlab与VC混合编程技术，建立磨机负荷预测仿真平台，实现了球磨机负荷参数的预测仿真。经过SVM参数优化后，模型的预测准确率更高，证实了该方法的可行性和有效性，为磨矿过程优化控制提供了有力的技术支撑。

[1]石立，张国旺，肖骁.金属矿山选矿厂磨矿分级自动控制研究现状[J].金属材料与冶金工程，2014（1）：43-48.

[2]WEI D H，CRAIG I K.Grinding mill circuits a survey of control and economic concerns[J].International Journal of Mineral Process，2009，90（14）：55-56.

[3]HUANG P，JIA M P，ZHONG B L.Investigation on measuring the fill level of an industrial ball mill based on the vibration characteristics of the mill shell[J].Minerals Engineering，2009，22（14）：1200-1208.

[4]TANG J，ZHAO L J，ZHOU J W，et al.Experimental analysis of wet mill load based on vibration signals of laboratory scale ball mill shell[J].Minerals Engineering，2010，23（9）：720-730.

[5] 冯雪，赵立杰，郑瀚洋.基于KPCA频谱特征提取的球磨机负荷检测方法 [J].沈阳化工大学学报，2014，28（2）：175-180.

[6]汤健，赵立杰，岳恒，等.基于多源数据特征融合的球磨机负荷软测量[J].浙江大学学报（工学版），2010，44（7）：1406-1413.

[7]纪昌明，周婷，向腾飞，等.基于网格搜索和交叉验证的支持向量机在梯级水电系统隐随机调度中的应用[J].电力自动设备，2014，34（3）：125-131.

[8]周华平，熊博杰，桂海霞.最小二乘支持向量机优化模型在煤矿安全预测中的应用[J].测绘科学，2014，39（7）：150-154.

[9]张炎欣，王伟，张航.基于即时学习策略的火电厂球磨机负荷软测量[J].计算机工程与应用，2012，48（7）：224-230.

[10]方帅，夏秀山，曹洋，等.基于噪声水平估计的图像盲去噪[J].模式识别与人工智能，2015，28（1）：51-57.

[11]李翠平，郑瑶瑕，张佳，等.基于遗传算法优化的支持向量机品位插值模型[J].北京科技大学学报，2013，35（3）：837.

[12]崔晓祥，李娟.基于支持向量机回归的电力系统负荷建模[J].江苏电机工程，2012，31（3）：37.

[13]ITO K，NAKAMO R.Optimiznig support vector regression hyperparameters based on crossvalidation[C]∥Proceedings of the international Jonit Conference on Neural Networks，2003，3（7）：2077-2081.

（编辑：刘杨）

Forecast of SVM mill load based on grid search and cross validation

LUO Xiaoyan，CHEN Huiming，LU Xiaojiang，XIONG Yang
（School of Mechanical and Electrical Engineering，Jiangxi University of Science and Technology，Ganzhou 341000，China）

In order to address the problem that mill load (ML)state only can be estimated with expert experience and ML parameters directly relevant to ML and ML state are hard to be monitored during actual production.This article proposed the method of combining grid search and cross validation to optimize SVM parameters and solve the problem of subjective selection between SVM kernel function parameter g and penalty factor C，by analyzing and reflecting vibration signal inside mill，extracting spectrum signature of signal and establishing forecasting model for mill load parameters by using support vector machine（SVM）.Forecast simulation of ball mill load parameter was achieved by establishing simulation platform based on hybrid programming of Matlab and VC. Both training mean square error（MSE） and square correlation coefficient（r2） obtained under optimized SVM parameters are higher than the forecasting results under default SVM parameters by respectively substituting default SVM parameters and optimized SVM parameters into ML regression forecasting model and ML parameter forecasting and comparison.

mill load；grid search；cross validation；parameter optimization；hybrid programming

A

：1674-5124（2017）01-0132-04

10.11857/j.issn.1674-5124.2017.01.027

2016-06-22；

：2016-07-20

国家自然科学基金项目（51464017）；江西省高等学校科技落地计划项目（KJLD1304（45））

罗小燕（1967-），女，江西赣州市人，副教授，硕士生导师，研究方向为机电系统智能监测与控制。