不同埋深盾构隧道开挖面稳定问题数值模拟
孙潇昊 缪林昌 林海山
(东南大学岩土工程研究所, 南京 210096)
不同埋深盾构隧道开挖面稳定问题数值模拟
孙潇昊 缪林昌 林海山
(东南大学岩土工程研究所, 南京 210096)
通过对照物理模型试验,采用二维颗粒流程序(PFC2D)对不同埋深和不同密度条件下的盾构掘进过程进行数值模拟,从而分析开挖面前方土体破坏机理.首先通过研究支护力和地表沉降的变化规律,将模型箱试验结果和数值模拟结果进行对比分析,分别确定了极限支护力;利用二维颗粒流程序对土拱效应进行研究,揭示了开挖面前方土体的失稳破坏机理.结果表明,支护力和地表沉降的变化规律都可分为2个阶段,且不受埋深条件的影响;发生局部失稳破坏后,土拱继续向上发展最终导致整体失稳破坏;埋深比较小时,未能形成土拱,而埋深比较大时,滑动区与土拱区随埋深比的增大而增大.数值模拟结果与模型箱试验结果基本一致,验证了采用纵面进行颗粒流模拟的可行性,因此可利用PFC2D进行深入颗粒流模拟.
盾构隧道;不同埋深;开挖面稳定性;颗粒流模拟
近年来,盾构施工技术由于具有施工机械化程度高、对周围环境影响小、施工快速等优势得到了广泛应用[1].施工时,既要保持开挖面稳定性,还要在控制地基的沉降同时避免支护力过小造成的前方土体过大沉降(甚至坍塌)和支护力过大可能导致的地表隆起.
周小文等[2]针对开挖面稳定问题通过物理模型试验研究了不同地层的开挖面破坏模式.物理模型试验方法称为宏观分析法,而土体的宏观表现与其内在细、微观特性相关,要研究土颗粒的微观特点,就需要采用模拟仿真方法研究盾构推进的破坏机理.因此,Fakhimi等[3]运用 PFC2D对岩石中的开挖问题进行了模拟,研究了圆洞周围的破坏情况.曾庆有等[4]用二维颗粒流程序对各种移动模式的刚性挡墙被动土压力进行了模拟,将计算结果与试验结果进行了对比.Funatsu等[5]利用程序PFC2D研究单个和平行隧道的衬砌加固稳定性.
目前,大多数学者都通过对应力大小进行控制来模拟研究开挖面稳定性[6-7],大部分采用FLAC方法进行模拟,而较少采用PFC2D离散元研究各因素对开挖面稳定的影响.因此,本文采用模拟简便且计算量少的位移控制方法,考虑不同埋深和密度条件,对照物理模型箱试验,采用PFC2D数值模拟开挖面的位移分析土体破坏情况,并研究支护力和地表沉降的变化规律,同时对极限支护力进行确定,然后在此基础上,通过土拱效应进一步了解失稳破坏机理.
1 模型箱试验
1.1 试验设备
采用室内盾构隧道物理模型箱进行试验,如图1所示.模型箱尺寸为长30 cm、宽30 cm和高50 cm;侧壁由钢化有机玻璃制成.根据对称性,设置外径和长度均为10 cm的半圆形隧道,将模型箱固定于距离底部5 cm处的模型内;厚度为1 cm的半圆形金属支护板用于模拟盾构开挖面,支护板可前后移动,移动速度控制在0~9.99 mm/min之间;采用微型土压力盒测定开挖面处的压力,将此压力近似等效为开挖面的支护力.

图1 模型箱实物图
1.2 试验材料及试验过程
试验采用江砂,烘干后进行颗粒分析试验,颗粒分析曲线如图2所示.由图颗粒分析可得,砂土为中砂,比重为2.65,级配不均匀.进行砂土直剪试验后,忽略砂与箱体有机玻璃的摩擦,同时忽略其尺寸效应,得到砂土密度1.5,1.6和1.7 g/cm3对应的内摩擦角分别为31.2°,35.2°和40.0°.

图2 模型试验用砂颗粒级配曲线
由于应力控制方法操作复杂且不易控制,本文参照Kirsch[8]的模型采用位移控制方式模拟盾构隧道开挖面失稳破坏的发展过程,即通过控制支护板后退位移模拟支护力减小时开挖面土体的变化.同时利用PIVview2C软件对试验全过程拍摄的照片进行处理和分析.试验过程中,将数码相机通过支撑架固定于模型箱正前方,以获得清晰稳定的模型箱全图,同时利用土压力微应变记录仪器Datataker对土压力盒进行二次标定,试验原理示意图如图3所示.

图3 模型箱试验原理图
控制3种砂土的干密度为1.5,1.6和1.7 g/cm3;每种密度分别对应埋深比1,2,3(上覆土深度C与开挖面直径D的比值),即共9组试验.设定支护板速度为1.0 mm/min,每隔15 s拍照一次,并记录土压力数据,得到极限支护力、土压力变化情况和开挖面失稳模式等.
2 数值模拟
2.1 模型构建及参数选取
模型尺寸为宽30 cm、长60 cm,上边界采用自由边界,其他边界则进行接触约束,支护板盾构隧道直径10 cm,长度10 cm,如图4所示.模拟过程中颗粒设置为莫尔-库仑材料,通过双轴数值模拟试验调整细观参数.颗粒接触模型采用线性刚度模型,边界和颗粒之间接触采取liner单元,即能够进行滑动,存在压力而没有拉力.用单位厚度圆形单元模拟砂土颗粒,建立初始细观参数.根据粒径及孔隙率生成颗粒集合体,并赋予其摩擦系数、密度及刚度.最后考虑摩擦系数、孔隙率、颗粒接触刚度对应力应变曲线的影响,并对照室内常规三轴试验进一步进行调整,最终得到模拟颗粒粒径为0.3~1.8 mm,密度为1.60 g/cm3,孔隙率为0.166和摩擦系数为1.9.

图4 埋深比为3的PFC2D计算模型
2.2 模拟方法
首先定义上、下、左、右4道墙体,参考文献[9-10]采用自然堆积砂土的方法得到颗粒的法向刚度和切向刚度均为140 MN/m,模型箱4道墙体的法向刚度和切向刚度均取为200 MN/m.为方便观察和选择合适的循环编程语句,采用埋深比为3进行模拟.
在重力作用下循环运算至初始应力平衡状态后,将整个模型的位移场及速度场清零.然后挖去左下方盾构处部分颗粒,模拟盾构隧道开挖,重新达到平衡.再对照物理模型试验,删除支护板墙体.迭代循环后,使得开挖面位移为1 mm,将开挖面各节点轴向位移进行固定,并通过布设在开挖面前方的测量圆,记录砂土颗粒的位移变化情况和轴向节点力,如图5所示.以此类推,直至开挖面位移为2 cm.
用程序PFC2D控制不同埋深比(1,2和3)和不同密度(1.5,1.6和1.7 g/cm3)模拟单因素对盾构隧道开挖面稳定破坏机理的影响.
3 数值模拟与模型箱试验结果比较
为了避免三维计算量过大的问题,本文采用二维颗粒流程序对盾构纵面进行近似模拟.由于模型箱试验土压力盒上下面也布置在竖向支护板直径处,因此两者等效,通过模拟可了解盾构开挖过程中应力状态变化、土颗粒位移时变规律和开挖面失

图5 测量圆布设图
稳时变规律,进一步认识开挖面失稳机理.由于采用二维程序模拟三维问题,需要将数值模拟结果与模型箱试验的结果进行对比来验证采用纵面进行颗粒流数值模拟得到结果的准确性,并判断程序PFC2D是否可作为深入颗粒流模拟的应用程序.
3.1 开挖面极限支护力
模型支护板类似于盾构土压仓隔板,隔板上的压力等于土压仓内土体作用在隔板上的压力,所以模拟中将支护板上压力作为开挖面支护力.通过图5布置的测量圆研究随着支护板后退位移的增大,开挖面前方土体平均土压力的变化规律,限于篇幅,本文只列出离开挖面最近的一列测量圆得到的平均土压力.如图6所示, 前上方土体的平均土压力先略有增大后趋于稳定,最后有所减小.而下方土体的平均土压力一开始有所减小,之后趋于稳定.不同埋深比和密度条件下得到的平均土压力随开挖面位移的变化规律基本相似.

图6 土体平均土压力随开挖面位移变化
模型箱试验和数值模拟研究得到在不同埋深和密度条件下支护力变化规律基本相似.支护力变化经历了减小和稳定2个阶段.① 减小阶段.一开始支护力迅速呈线性减小,之后减小速度有所变缓,直到最小值,一般定义最小值为极限支护力,且此时支护板水平位移约3 mm.② 稳定阶段.支护力稍有回升,最后逐渐趋于稳定值,如图7所示.通过随机生成模拟颗粒数量,多次模拟取平均值得到极限支护力(见表1).由表可知,模型箱试验和数值模拟得到的极限支护力较为接近,这是因为模型箱试验和数值模拟研究的平面可近似为同一平面,而数值模型的极限支护力较小主要是由于采用圆形颗粒单元模拟砂土颗粒,所生成颗粒数目较少.

(a) 模型箱试验
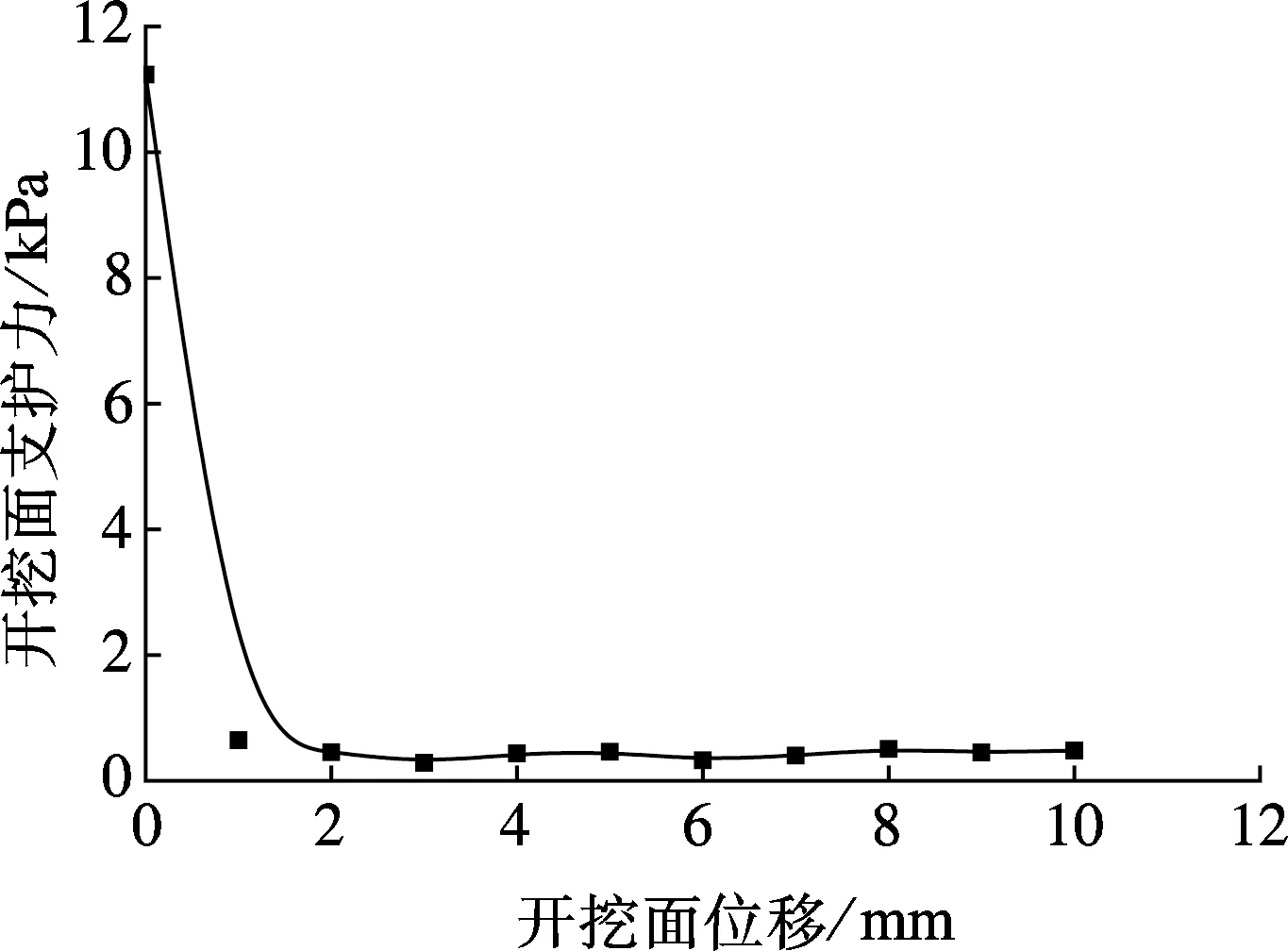
(b) 数值模拟

密度/(g·cm-3)埋深比压力/kPa模型箱试验数值模拟1.510.110.091.520.130.101.530.160.121.610.150.121.620.200.161.630.270.231.710.240.191.720.280.241.730.340.28
3.2 地表位移
利用软件PIVview2C对全过程所拍摄的照片进行对比分析发现,不同埋深比条件下地表沉降可大致分为2个阶段:第1阶段为地表无沉降,如图8所示,埋深比越大,该阶段持续时间越长;第2阶段出现沉降,先缓慢沉降,埋深比越大,沉降速度越快,如图9所示,到达临界沉降后再加速沉降,且增长速率越来越大,最后以一定值快速沉降,但不同埋深比下,沉降速度大致相同.

(a) 埋深比1
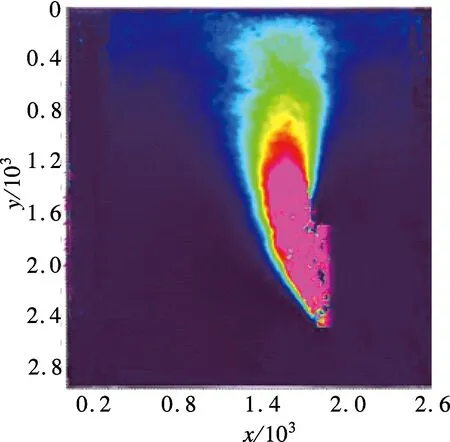
(b) 埋深比2

(c) 埋深比3

(a) 埋深比1

(b) 埋深比2

(c) 埋深比3
数值模拟时采用测量圆检测的位移位置和模型箱试验一致.支护板刚开始位移时,破坏区局部土体首先达到极限平衡状态,数值模拟得到的结果和模型箱试验结果大致相同,位移从开挖面逐渐向上发展,地表一开始没有检测到位移,之后发生缓慢的竖向位移.随着开挖面不断更新,地表沉降以变化不大的速度缓慢下沉,没有出现模型箱试验中到达临界沉降后,地表沉降迅速增加的现象,因此,数值模拟中没有临界沉降.在不同埋深条件下都出现相同这种现象.这是因为PFC2D假设颗粒为单位厚度的圆形颗粒,颗粒间的剪切作用不明显,无法很好地观察到最后的整体失稳破坏,但之前的模拟情况都与模型箱试验较为吻合.
开挖面前方土体松动后,土颗粒发生水平位移.但水平位移不是主要的,竖向位移才会对周围环境造成极大的影响.开挖面位移引起的土体竖向沉降为开挖面前方1.0D×0.75D的范围,如图10所示.
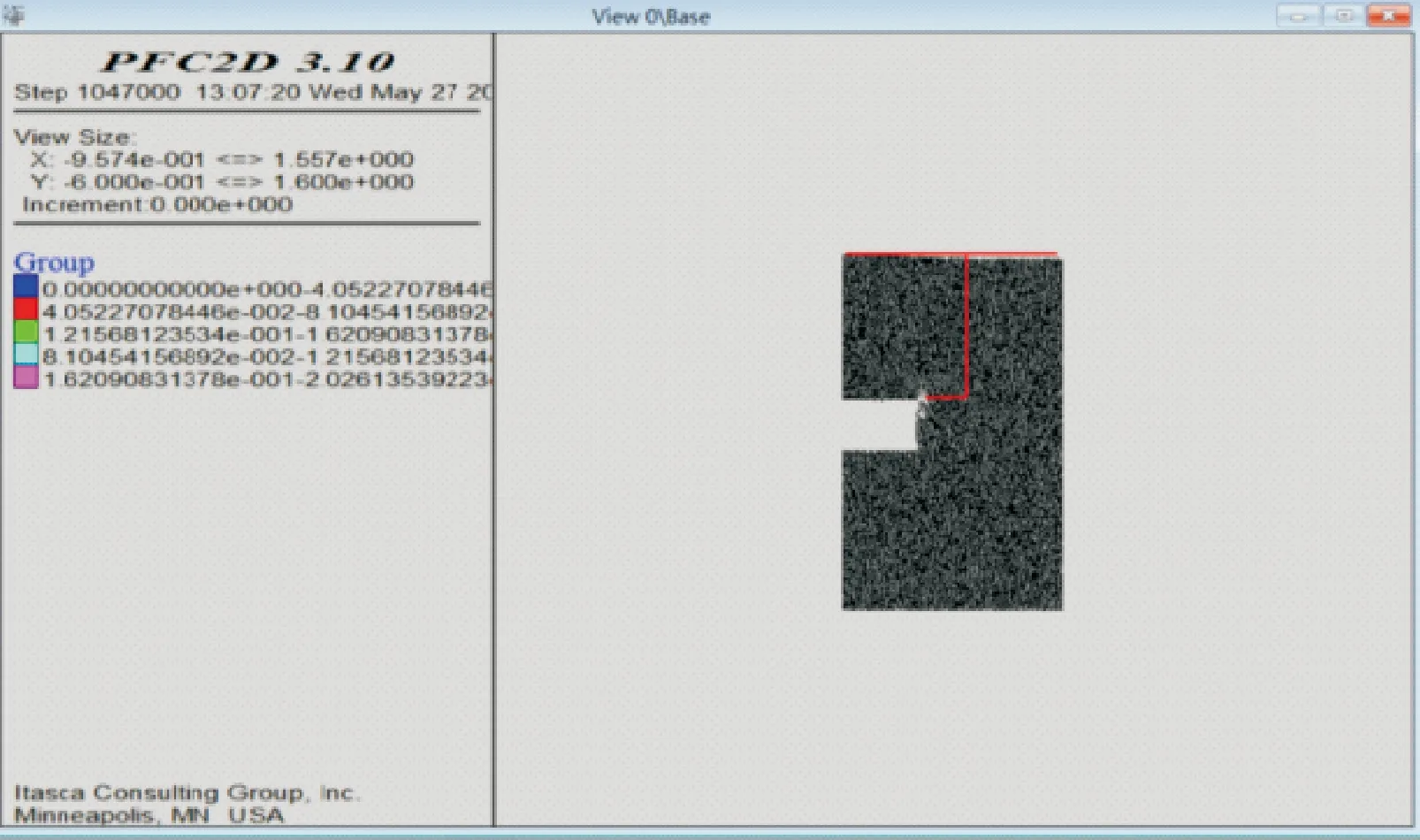
图10 表面颗粒竖向位移图
3.3 开挖面失稳模式及土拱效应
随着开挖面位移加大,支护力减小,开挖面前方土体的应力场发生了变化,竖向和水平应力同时减小,产生松动破坏区.但开挖面上方1.0D~1.5D处的水平土压力增大,前方区域土体竖向土压力增大,水平土压力减小,因此传递土压力形成土拱,如图11(a)、(b)所示.支护板继续位移,破坏位置逐渐向地表延伸,土拱区也逐渐向上延伸,如图11(c)、(d)所示.因此,土拱的产生、发展直至消失与开挖面前方土体的应力变化密切相关,通过研究其应力可以很好地解释土拱效应.
开挖面支护力减小导致开挖面前方土体应力重分布,引起的土拱效应对开挖面稳定性及地表沉降产生重要影响.
当埋深比为1时,随着开挖面位移的增加,在还没有形成土拱时,破坏区就逐渐发展至地表,形成贯通至地表的滑动面.当埋深比为2和3时,随着开挖面位移增加,破坏区土体与两侧土体形成土拱,土拱向上发展到地表并最终破坏,转化为滑动区.埋深比越大,土拱发展至地表越慢,滑动区与土拱区越大.

(a) 位移为0

(b) 位移为2 mm

(c) 位移为6 mm

(d) 位移为10 mm
武军等[11]的研究表明,支护板位移使开挖面前方土体逐渐发生破坏,慢慢形成土拱,发生局部失稳破坏,之后土拱效应消失,出现松动破坏区,使土体发生整体失稳破坏.这与本文的研究结论相似,因此可以得出,由于土拱的作用,使得极限支护力比初始土压力小得多.
4 结论
1) 当埋深条件不同时,支护力变化规律一致:首先迅速降低,之后速度减缓并逐渐降低到最小值,然后支护力有所回升,最终趋于一稳定值.
2) 当埋深条件不同时,地表沉降变化规律一致:开始几乎无沉降,然后缓慢沉降,接下来沉降速度越来越快,最后沉降迅速发展.
3) 开挖面支护力减小使前方土体形成松动区,出现土拱现象,发生局部失稳破坏,此时支护力为极限支护力.之后土拱逐步向上发展并最终消失,出现整体失稳破坏.
4) 当埋深比较小时,未能及时形成土拱,直接形成贯通至地表的滑动面.而埋深比较大时,则会出现土拱的形成与发展.埋深比越大,土拱发展至地表越慢,滑动区与土拱区更大.
5) 利用PFC2D颗粒流程序对开挖面前方破坏区土体的应力变化规律进行数值模拟研究,结果表明数值模拟结果和模型箱试验结果具有一致性.
References)
[1]丁春林,周书明,周顺华.盾构施工对隧道围岩内力和地层变形的影响[J].中国公路学报,2002,15(4):62-65. DOI:10.3321/j.issn:1001-7372.2002.04.017. Ding Chunlin, Zhou Shuming, Zhou Shunhua. Shield construction’s influence on the surrounding rocks’ inner force for the tunnel and stratum deformation[J].ChinaJournalofHighwayandTransport, 2002, 15(4): 62-65. DOI:10.3321/j.issn:1001-7372.2002.04.017. (in Chinese)
[2]周小文,濮家骝.砂土中隧洞开挖引起的地面沉降试验研究[J].岩土力学,2002, 23(5):559-563. DOI:10.3969/j.issn.1000-7598.2002.05.007. Zhou Xiaowen, Pu Jialiu. Centrifuge model test on ground settlement induced by tunneling in sandy soil[J].RockandSoilMechanics, 2002, 23(5): 559-563. DOI:10.3969/j.issn.1000-7598.2002.05.007. (in Chinese)
[3]Fakhimi A, Carvalho F, Ishida T, et al. Simulation of failure around a circular opening in rock[J].InternationalJournalofRockMechanicsandMiningSciences, 2002, 39(4): 507-515. DOI:10.1016/s1365-1609(02)00041-2.
[4]曾庆有,周健.不同墙体位移方式下被动土压力的颗粒流模拟[J]. 岩土力学, 2005,26 (增刊1):43-47. Zeng Qingyou, Zhou Jian. Analysis of passive earth pressure due to various wall movement by particle flow code (2D)[J].RockandSoilMechanics, 2005, 26(S1): 43-47. (in Chinese)
[5]Funatsu T, Hoshino T, Sawae H, et al. Numerical analysis to better understand the mechanism of the effects of ground supports and reinforcements on the stability of tunnels using the distinct element method[J].TunnellingandUndergroundSpaceTechnology, 2008, 23(5): 561-573. DOI:10.1016/j.tust.2007.10.003.
[6]Zhang C, Han K, Zhang D. Face stability analysis of shallow circular tunnels in cohesive-frictional soils[J].TunnellingandUndergroundSpaceTechnology, 2015, 50: 345-357. DOI:10.1016/j.tust.2015.08.007.
[7]Lee Chung-Jung, Chiang Kuo-Hui, Kuo Chia-Ming. Ground movement and tunnel stability when tunneling in sandy ground[J].JournaloftheChineseInstituteofEngineers, 2004, 27(7): 1021-1032. DOI:10.1080/02533839.2004.9670957.
[8]Kirsch A. Experimental investigation of the face stability of shallow tunnels in sand[J].ActaGeotechnica, 2010, 5(1): 43-62. DOI:10.1007/s11440-010-0110-7.
[9]周国庆,周杰,陆勇,等.颗粒流程序(PFC2D)中阻尼参数的适用性研究[J].中国矿业大学学报,2011,40(5):667-672. Zhou Guoqing, Zhou Jie, Lu Yong, et al. Selection of damping parameters used in a particle flow code(PFC2D)[J].JournalofChinaUniversityofMining&Technology, 2011, 40(5): 667-672.(in Chinese)
[10]朱伟,钟小春,加瑞.盾构隧道垂直土压力松动效应的颗粒流模拟[J].岩土工程学报,2008,30(5):750-754. DOI:10.3321/j.issn:1000-4548.2008.05.021. Zhu Wei, Zhong Xiaochun, Jia Rui. Simulation on relaxation effect of vertical earth pressure for shield tunnels by particle flow code[J].ChineseJournalofGeotechnicalEngineering, 2008, 30(5): 750-754. DOI:10.3321/j.issn:1000-4548.2008.05.021. (in Chinese)
[11]武军,廖少明,时振昊.考虑土拱效应的盾构隧道开挖面稳定性[J].同济大学学报(自然科学版),2015,43(2):213-220. DOI:10.11908/j.issn.0253-374x.2015.02.008. Wu Jun, Liao Shaoming, Shi Zhenhao. Work face stability of shield tunnel considering arching effect[J].JournalofTongjiUniversity(NaturalScience), 2015, 43(2): 213-220. DOI:10.11908/j.issn.0253-374x.2015.02.008. (in Chinese)
Numerical simulation research on excavation face stability of different depths of shield tunnel
Sun Xiaohao Miao Linchang Lin Haishan
(Institute of Geotechnical Engineering, Southeast University, Nanjing 210096, China)
By comparing with physical model tests, two-dimensional particle flow code (PFC2D) was used for numerical simulation of the tunnel excavation process to analyze soil failure mechanism under various buried depths and densities. First, the variations of the support force and the surface subsidence were studied and the results of model tests and numerical simulation were comparatively analyzed. Then, the limit support force was determined. Finally, the failure mechanism of the soil in front of the excavation face was further understood by utilizing PFC2Dto study the soil arch effect. The results show that the changes of the supporting force and the ground settlement can be divided into two stages, and are not affected by the buried depth; the soil arching continues to be developed after the local failure, leading to the overall instability; when the depth is smaller, the soil arching fails to be formed, otherwise, the sliding zone and the soil arching region enlarge with the increase of the buried depth. The consistency of results of numerical simulation and physical test verifies the feasibility of particle flow simulation with longitudinal surface. Therefore, PFC2Dcan be used in depth for particle flow simulation.
shield tunnel;different depths;excavation face stability;particle flow simulation
第47卷第1期2017年1月 东南大学学报(自然科学版)JOURNALOFSOUTHEASTUNIVERSITY(NaturalScienceEdition) Vol.47No.1Jan.2017DOI:10.3969/j.issn.1001-0505.2017.01.028
2016-06-07. 作者简介: 孙潇昊(1993—),男,博士生;缪林昌(联系人),男,博士,教授,博士生导师,Lc.miao@seu.edu.cn.
国家自然科学基金资助项目(51578147,51278099).
孙潇昊,缪林昌,林海山.不同埋深盾构隧道开挖面稳定问题数值模拟[J].东南大学学报(自然科学版),2017,47(1):164-169.
10.3969/j.issn.1001-0505.2017.01.028.
U45
A
1001-0505(2017)01-0164-06
——结构相互作用的影响分析

