MapReduce框架下的Skyline结果优化算法*

马学森, 王晓洁, 韩江洪, 王营冠

(1.合肥工业大学 计算机与信息学院，安徽 合肥 230009;2.中国科学院 上海微系统与信息技术研究所 无线传感网络与通信重点实验室,上海 200050)

MapReduce框架下的Skyline结果优化算法*

马学森1,2, 王晓洁1, 韩江洪1, 王营冠2

(1.合肥工业大学 计算机与信息学院，安徽 合肥 230009;2.中国科学院 上海微系统与信息技术研究所 无线传感网络与通信重点实验室,上海 200050)

随着大数据时代的到来，数据量和数据复杂度急剧提高，Skyline查询结果集规模巨大，无法为用户提供精确的信息。MapReduce作为并行计算框架，已广泛应用于大数据处理中。本文提出了MapReduce框架下基于支配个数的结果优化算法(MR-DMN)，解决了大数据环境下的Skyline结果集优化问题。大量的实验表明：算法具有良好的时间和空间效率。

大数据; MapReduce; Skyline; 支配个数

0 引 言

Skyline查询[1]是指从给定数据集中选择一组不被其他数据支配的数据，所谓支配是指一个数据在所有维度上都不比其他数据差，且至少在一个维度上优于其他数据。典型的Skyline查询例子是业务选择问题，由于经营调整，企业需要保留一些销量高且单件利润高的业务，Skyline查询的结果集是销量和利润上都不比其他业务差，且至少在一个属性上优于其他的业务。Skyline查询广泛应用于用户推荐、决策支持以及数据可视化等领域。

在现实生活中，数据在各个维度上的取值是有优有劣的，随着数据维度的增大，支配的条件越来越难满足，一个点支配另一个点的可能性越来越小，因此,结果集中将包含很多互不支配的数据点。随着大数据环境下数据量和数据复杂度的提高，Skyline查询结果集的规模急剧增大。在随机数据集中，Skyline结果集数量为Θ(lnd-1n/(d-1)!)[2]。

如何为用户选取规模较小，更具有代表性的结果集，提高大数据下Skyline结果集的质量，成为急需解决的问题。近年来兴起的MapReduce并行计算框架[3]广泛应用于大数据及云计算[4]处理中，本文将Skyline结果集优化算法与MapReduce框架相结合，提出了大数据下Skyline结果集优化算法。提出了MapReduce框架下的基于支配个数的算法(MapReduce dominant number-based algorithm,MR-DMN)。实验结果表明：MR-DMN具有良好的时间和空间性能。

1 相关工作

1.1 基本概念

Skyline查询是指从给定的一个d维空间数据点集合D中选择一个子集，该子集中的任意一个点都不能被D中其他点所支配。具体来说，给定d维数据空间S={s1,s2,…,sd}(d∈N*)上的数据集合D={P1,P2,…,Pn}(n∈N*)，D中的每一个数据点Pi是S空间中的一个d维数据点，Pi.sj表示数据点Pi的第j维度的值。为了简便，不失一般性，本文中假设数据点越大越优。

定义1支配(dominate)：给定数据集D中的两点Pi,Pj(i,j∈[1,n])，称Pi支配Pj,当且仅当对于∀si∈S(i∈[1,d])，都有Pi·si≥Pj·si，并且∃t∈[1,d]，使得Pi·st>Pj·st。

定义2Skyline集(Skyline(D))：对于∀Pi∈D，称Pi为D中的Skyline点, 当且仅当在D中不存在支配Pi的数据点。D中所有Skyline数据点构成了D上的Skyline数据集，记作Skyline(D)。

1.2 Skyline结果集优化算法

为了对Skyline查询结果集进行优化，为用户返回更具有代表性的结果集。有学者提出返回k个最具有代表性的结果点代表整个结果集，该算法主要分为以下三类：

1)Top-k查询算法

Top-k查询算法[5]利用单调打分函数对每个数据的维度值进行聚集，得到单一的打分值，按照打分值对所有数据进行排序，选出前k个数据作为最终结果返回给用户。例如在图1的示例中，假设打分函数为F=x+y，则top-3查询结果为B(6,9),C(7,8),D(9,7)三点。top-k查询的优势是用户可以通过参数k控制返回结果的数量，由于结果对象的选取依赖于打分函数，因此,适当地选取打分函数成为解决问题的关键。同时，Top-k查询的结果是根据打分函数选择的，数据点之间没有进行支配比较，因此,其结果不一定是Skyline点。

图1 原始数据集示例

2)Top-k支配

同样为了有效地返回k个具有代表性的结果点，top-k支配(top-k dominating)查询[6]的主要思想是，一个点的重要程度可以用该点所支配的其他点个数μ(p)来衡量。top-k支配查询根据μ(p)值对数据集排序，返回μ(p)值最高的k个点作为查询结果。例如，图2示例中top-4支配查询的结果是B(6,9),C(7,8),D(9,7),E(9,5)。

文献[6]提出了计算top-k支配查询的基本方法，即先计算原始数据集的Skyline集，找到top-1支配Skyline点p，之后将p移出数据集D，迭代查找下一个点，直到找到k个点。文献[7]对传统的R-tree算法改进，得到聚合R-tree，该算法可以并行计算数据点的打分值，依据打分值优先级遍历搜索所有树节点。当数据量很大时，构建索引的代价将非常大。文献[8]提出了分布式环境下的top-k支配查询，避免了多余的通信开销和延迟。

3)k个最具有代表性的Skyline点查询算法

在top-k支配查询算法中仍存在一些问题，该算法的结果可能包含非Skyline点，如在上述例子中，top-4支配查询结果中的E(9,5)不是Skyline点。这也反映出Skyline查询的特点：在Skyline计算中，尽管一个点支配了很多非Skyline点，最终仍可能被其他Skyline点支配掉，无法成为Skyline点。相反可能有些点支配其他点的个数并不多，它仍是Skyline点，如图2中的点A(1,10)。

为了解决top-k支配存在的问题，Lin X M等人提出从Skyline结果集中选择k个最有代表性的Skyline点(top-krepresentative skyline points,top-kRSP)查询算法[9]。给定一个数据集D和参数k，得到包含k个Skyline点的集合S，使得|D(S)|取得最大值，|D(S)|表示所有被S中的点支配的点的数量。Top-kRSP算法兼具了Skyline查询和Top-k查询的优点，不需要依赖具体的打分函数，且有效控制了Skyline查询结果集数量。

作者提出了针对二维数据Top-kRSP查询的动态编程算法，该算法的内存开销为O(m2)(m为Skyline点数量)。作者证明三维及以上数据的top-kRSP算法是NP-hard问题，提出贪婪算法(greedy algorithm,GDY)[9]，算法首先计算出所有Skyline结果，接着再次扫描数据集计算出每个Skyline点的支配个数，得到支配个数最多的k个点。为了保存每个Skyline点支配数据点的内存开销为O(mn)(n为数据集D的大小)，当维度达到5维时，45 %的被支配点会被写入内存中，将产生很大的I/O开销。

1.3 MapReduce并行计算框架

MapReduce是一个分布式并行计算框架，已广泛应用于大数据的计算中。它的基本思想是分治法，主要由两个阶段的任务组成：Map Task和Reduce Task。对于具有较少依赖关系的数据，用一定的数据划分方法对数据进行划分，每个数据分片交给一个Map Task处理，Reduce Task负责对Map的结果进行汇总整理和输出。Map Task将读取的数据分片解析为(key，value)对，调用用户自定义的map()函数进行处理，并将结果映射成新的(key，value)对存放在本地磁盘上；Reduce Task读取Map Task的结果，调用reduce()函数处理，最后按照(key，value)对的形式输出到HDFS文件系统上。Map和Reduce任务在输出数据时，会按照key值对数据记录排序输出。

2 MapReduce下的top-k RSP算法

传统的top-kRSP算法通常采用索引结构，数据点建立索引将产生巨大的内存和I/O开销，无法应用于大数据环境。GDY不需要构建索引，但需要多次遍历整个数据集求出每个Skyline点支配的其他点，需要大量额外的内存空间保存被支配的点，其时间和空间效率还有待提高。本文将GDY算法应用到MapReduce框架下，并对MR-GDY算法(MapReduce-based greedy algorithm, MR-GDY)进行改进，首次提出了大数据环境下的top-kRSP算法中的MR-DMN算法在进行数据支配比较的同时，记录每个点的支配个数，从而为用户返回支配个数最多的k个Skyline点。

2.1 MR-DMN算法原理

根据top-kRSP查询的定义，该算法返回Skyline结果集中k个支配个数最多的Skyline点。因此，MR-DMN算法在进行数据点间的支配比较时，记录每个数据点的支配个数。具体来说：窗口队列w用于保存暂时的Skyline点，进入窗口的数据点p将被附加一个标记位num(p)，用于标记该点支配的数据点个数。第一个数据点将被放入窗口中，num(p)置为0。接下来，每读取一个新的数据点q都会与窗口中的所有点进行比较，将会出现以下三种情况(新数据点q的初始num值为0)：

1)若窗口中存在点p支配q，则将q删除，由于支配具有传递性，p可以支配q支配的所有点，并且可以支配q，因此,更新num(p)，num(p)=num(p)+num(q)+1。

2)若点q支配窗口中的点p,则将p从窗口中删除,同时将q加入窗口队列。若q支配p，则q可以支配p所支配的所有点，并可以支配p,因此,num(q)=num(q)+num(p)+1。

3)若q与窗口中的所有点比较后，与所有数据点均互不支配，原来窗口中的点num值不变，将q加入窗口中，num(q)置为0。

MR-DMN算法的难点在于计算每个Skyline点的支配个数，在上述比较中，若点q被支配，则将它直接删除。然而可能其他点也会支配该点，由于失去了与该点比较的机会，其他点的num值可能会产生偏差。例如图2中的点G(3，8)，它同时被两个点B(6,9),C(7,8)支配，若G被B支配后被直接删除，那么G无法与C比较，C的支配个数将会比实际结果小1。因此，在MR-DMN算法中，若一个新点q被支配，不应立即将它删除，而将它与临时窗口中的所有点进行比较后再删除。与此同时产生另一个问题，即若此时C点还没有进入临时窗口中，C点也无法与G点进行比较，从而导致C的num值计算不准确。如果将支配能力[10]较强的点优先放在窗口中，那么它们与每个被支配的点都会有比较的机会，这样计算得出的num(p)会更准确。同时，若将支配能力强的点放在队列前面，可以避免后面的点支配前面的点，避免了数据的换入换出，从而加快Skyline结果的计算。因此，算法引入参考文献[10]中数据点支配能力的计算方法

(1)

在MR-DMN算法中，Map阶段首先对数据点按照支配能力大小进行排序，再进行数据点间的支配比较，在数据点支配比较的过程中记录每个数据点的num值，最后按照num值大小降序输出到Reduce阶段。在Reduce阶段，汇总所有Map阶段的输出结果，对所有数据点再进行一次支配比较，最终返回支配个数最大的k个Skyline点。

2.2 MR-DMN算法流程

1)Map阶段：整个数据集被划分到2个Map任务中，在每个Map任务中数据点进行排序后，开始数据点间的支配比较。在第一个Map任务中，数据点(7,8)分别支配数据点(5,6),(4,7),(3,8),(4,6),(5,4),(6,3),(3,2)，共7个数据点，因此,num(7,8)=7。同理,num(6,9)=7，(1,10)由于未支配任何数据点，num(1,10)=0。在第二个Map任务中，数据点(8,7)支配点(7,7),(6,7),(8,5),(7,4),(6,4),(4,5)，num(8,7)=6，(9,6)支配了点(8,5),(9,4),(7,4),(6,4),(4,5)，num(9,6)=5,num(10,2)=0。当所有数据点比较结束后，每个Map任务的结果按照num(p)值降序输出到Reduce阶段。

2)Reduce阶段：汇总所有Map任务的输出结果，对所有数据点再进行一次支配比较。数据点(8,8)支配点(7,8)，因此,num(8,8)=num(8,8)+num(7,8)+1=6+7+1=14。所有数据点比较结束后，输出k个num(p)值最大的Skyline点，本例中取k值为3，最终结果为(8,8),(6,9), (9,6)。MR-DMN算法流程如图2所示。

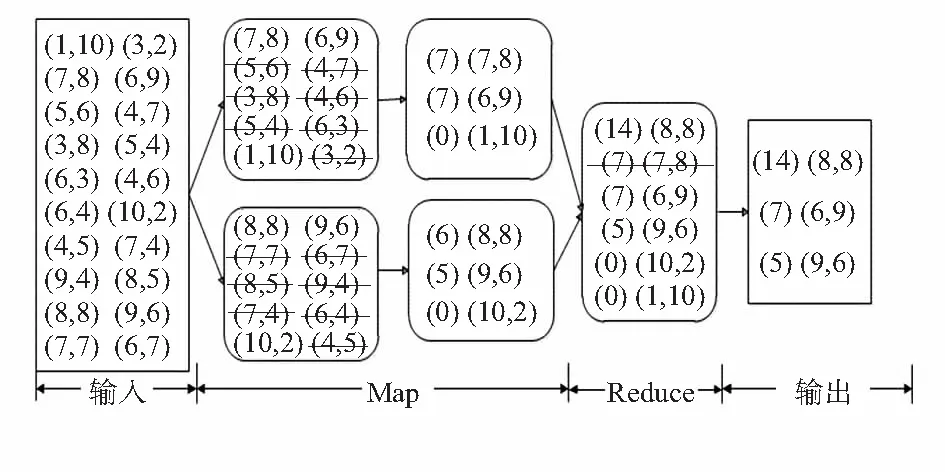
图2 MR-DMN算法流程

3 MR-DMN算法实验

3.1 实验环境

本文实验用机的配置为：内存4GB，操作系统为Windows7，处理器为Intel(R)Core(TM)i5-3210MCPU@ 2.50GHz。在Ubuntu环境下模拟了Hadoop伪分布式环境，算法全部用Java实现，Eclipse的版本为3.3.2，在JDK1.6环境下编译，Hadoop的版本为0.20.2。

本文实验利用文献[1]中的标准数据生成工具生成了正相关、反相关和独立分布的实验数据。每个数据集的数据量为2～10M，数据维度从2～8变化，默认维度是5。将本文中提出的MR-DMN算法与MR-GDY算法进行比较。由于正相关分布下算法查询性能与独立分布下相似，因此,本次实验主要分析独立分布和反相关分布下的算法性能。

3.2 时间效率分析

1)本次实验测试了算法运行时间与数据量之间的关系，分别测试了反相关分布及独立分布下的4维数据，数据量从2M变化到10M的运行时间，实验结果如图3(a)和3(b)所示。随着数据量的增大，算法时间增加，独立分布数据集的运行时间远小于反相关分布下的运行时间。这主要是由于反相关分布数据各维度取值相异，在进行支配判断时需进行大量比较，因此算法运行时间较长。由于MR-GDY算法需要进行多轮全局的比较才能得出结果，而MR-DMN算法只需访问一次数据集即可求得结果，因此,MR-DMN算法运行时间有明显缩减。

图3 反相关及独立数据集运行时间与数据量关系

2)本次实验测试了算法运行时间与维数之间的关系，测试了在2M数据集下，反相关以及独立分布下数据维数由2变化到8的运行时间，实验结果分别如图4(a)和4(b)所示。从实验结果看，反相关分布的运行时间对维度比较敏感，当维度增大时，数据点间不相互支配的情况增多，从而导致结果集变大，运行时间增加。而独立分布下，结果集随维度增加变化不大，因此，算法运行时间的增加没有反相关分布下明显。

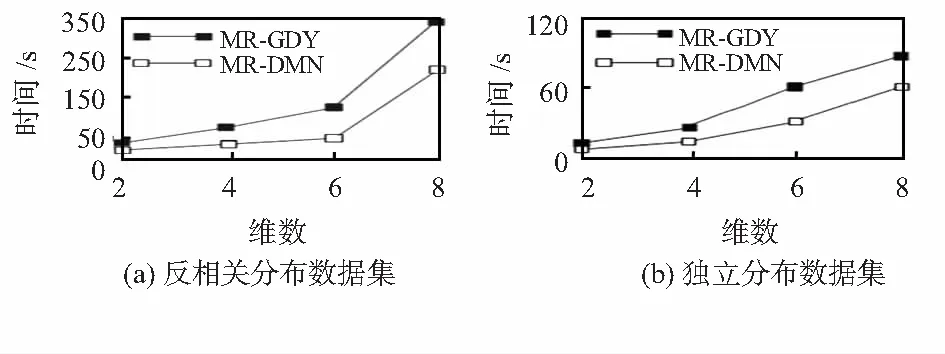
图4 反相关及独立数据集运算时间与维数关系

3)本次实验测试了算法运行时间与k值之间的关系。分别测试了反相关分布以及独立分布下，k值从10变化到50的运行时间变化，实验结果分别如图5(a)和5(b)所示。由于MR-GDY算法中需要不断合并新的数据点，因此,当k值增大时算法时间变长。

图5 反相关及独立数据集运行时间与k值关系

3.3 空间效率分析

由于MR-GDY算法需要保存所有Skyline点支配的点，因此将产生较大的内存开销。在二维数据集上，MR-GDY所需的内存空间为整个数据集的2倍，而当数据维度为5时，MR-GDY所需要的内存空间为整个数据集的数十倍以上。MR-DMN算法仅需要增加一位用于存储该数据点的支配个数，除此之外不需要额外的存储空间，所需内存空间最大为原始数据集的1+1/d倍(d为数据维数)，因此,MR-DMN具有良好的空间效率。

4 结 论

本文在分析了传统Skyline结果优化算法的基础上，针对大数据环境下的Skyline结果集优化问题，提出了MapReduce框架下基于支配能力的优化算法MR-DMN。MR-DMN在进行支配比较的同时，计算每个Skyline点的支配个数，选取支配个数最大的k个点作为返回结果。实验结果表明:MR-DMN算法在大数据环境下，相对于传统的MR-GDY算法，时间效率和空间效率有了明显的提高。

[1]BorzsonyiS,KossmannD,StockerK.TheSkylineoperator[C]∥Proceedingsofthe17thInternationalConferenceonDataEngineering(ICDE),2001:421-430.

[2]ChanC,JagadishHV,TianKL,etal.Onhighdimensionalskylines[C]∥AdvancesinDatabaseTechnology,2006:478-495.

[3] 张建平,李 斌,刘学军,等.基于Hadoop的异常传感数据时间序列检测[J].传感技术学报,2014,27(12):1660-1665.

[4] 刘东平,马利亚,杨 军.云环境下异构无线传感器网络节点调度改进算法[J].传感器与微系统,2015,34(10):128-132.

[5]TaoY,XiaoP．Efficientskylineandtop-kretrievalinsubspace-s[J].TransactionsonKnowledgeandDataEngineering,2007,19(8):1072-1088.

[6]YiuML,MamoulisN.Multi-dimensionaltop-kdominatingqueries[J].VLDBJournal,2009,18(3):695-718.

[7] 韩希先,杨东华.TKEP:海量数据上一种有效的Top-kDominating查询处理算法[J].计算机学报,2010,33(8):1405-1417.

[8]AmagataD,SasakiY.Efficientprocessingoftop-kdominatingqueriesindistributedenvironments[C]∥WorldWideWeb,2015:1-33.

[9]LinXM,YuanYD,ZhangQ,etal.Selectingstars-thekmostrepresentativeskylineoperator[C]∥The23rdInternationalConferenceonDataEngineering(ICDE),2007:86-95.

[10] 印 鉴,姚树宇,薛少锷,等.一种基于索引的高效k—支配Skyline算法[J].计算机学报,2010,33(7):1237-1245.

作者简介:

马学森(1977-)，男，博士，副教授，主要从事网络与信息安全、物联网研究工作。

Skyline result optimization algorithm based on MapReduce framework*

MA Xue-sen1,2, WANG Xiao-jie1, HAN Jiang-hong1, WANG Ying-guan2

(1.School of Computer & Information,Hefei University of Technology,Hefei 230009,China;2.Key Laboratory of Wireless Sensor Networks & Communication,Shanghai Institute of Microsystem and Information Technology,Chinese Academy of Sciences,Shanghai 200050,China)

With the advent of big data,data volume and complexity increase drastically,Skyline query result set is so large that it can’t provide precise information to the users.As parallel computing framework,MapReduce has been widely applied to big data processing.A result optimal algorithm, MapReduce-based dominant number algorithm(MR-DMN)is proposed,based on dominating number under MapReduce framework,which solves problem of optimization of Skyline result set in big data environments.Lots of experiments show that the algorithm has good time and space efficiency.

big data; MapReduce; Skyline; dominant number

2016—03—24

国家自然科学基金资助项目(61370088)；国家科技支撑计划资助项目(2013BAH51F01)；安徽省高校自然科学研究基金资助项目(KJ2012A233)；中国科学院无线传感网络与通信重点实验室开放课题资助项目(2013003)

10.13873/J.1000—9787(2017)02—0146—04

TP 274

A

1000—9787(2017)02—0146—04

林 娟(1992-)，女，通讯作者，硕士研究生，主要研究方向为信号处理。