融资融券在股灾阶段对市场波动性的影响分析

吉余峰 梁弋

[摘 要]2015的中国股市注定是让人难忘的一年。上证A股指数一路飙升至5 178点，再如过山车般的狂降至不足2 900点，如此巨幅的波动在世界范围内都是前所未见的。毒杠杆、无度配资、监管制度的缺失、强制平仓、恶意做空等一系列字眼，都充斥在我国尚不完善的资本市场之中。我国自2010年3月31日引入融资融券业务以来，对它的研究一直处于初步阶段，尚不明确其对于我国资本市场的影响；而对于造成这次“股灾”的原因，大部分矛头都指向融资与融券业务。本文在充分参阅国内外文献的基础之上，以GARCH与VAR模型相结合的实证分析方法着重研究“股灾”时段融资融券对上证A股指数波动性的影响。

[关键词]上证A股；融资；融券；波动性；GARCH；毒杠杆

doi：10.3969/j.issn.1673 - 0194.2017.02.068

[中图分类号]F224；F832.51 [文献标识码]A [文章编号]1673-0194（2017）02-0-03

0 引 言

2015年股市的热度早已超越了气候的温度，无论机构投资者还是中小投资者都在这一场指数狂飙的盛宴中尽情地享受。铺天盖地的都是众多投资机构的破万点论、牛市论，给投资者展示了我国资本市场一片大好的景象，可是风险也在进一步集聚，在等待它爆发的一天。

2015年5月25日，市场在经历过一次小幅调整后又向上创出年内新高，创业板指数也连连新高，各种小盘股活跃，中字头的大盘股开始横盘震荡，不久，指数就已经破了5000点的大关。5月28日上午10点半过后，第一波下跌行情开始，创业板领跌，高价股下跌，到下午2点45分后，更是一波3%幅度130多点的下跌，使市场上众多股票由涨停到跌停。顿时舆论四起，牛市泡沫的破裂也就在这一刻开始了。

1 研究模型選择

1.1 ARCH模型族介绍

1.1.1 ARCH模型族

ARCH模型的基本思想是指在以前信息集下，某一时刻一个噪声的发生是服从正态分布。该正态分布的均值为零，方差是一个随时间变化的量，即条件异方差。并且这个随时间变化的方差是过去有限项噪声值平方的线性组合，这样就构成了自回归条件异方差模型。

1.1.2 GARCH模型

自从Engle提出ARCH模型分析时间序列的异方差性以后，波勒斯列夫又提出了GARCH模型，GARCH模型是一个专门针对金融数据专门做的回归模型，除去和普通回归模型相同的之处，GARCH对误差的方差进行了进一步的建模，特别适用于波动性的分析和预测。

1.2 VAR模型

向量自回归（VAR）是基于数据的统计性质建立模型，VAR模型把系统中每一个内生变量作为系统中所有内生变量的滞后值的函数来构造模型，从而将单变量回归自回归模型推广到有多元时间序列组成的“向量”自回归模型。VAR模型是处理多个相关经济指标的分析与预测最容易操作的模型之一。

2 融资融券对上证A股指数波动性影响的实证分析

2.1 数据选择与说明

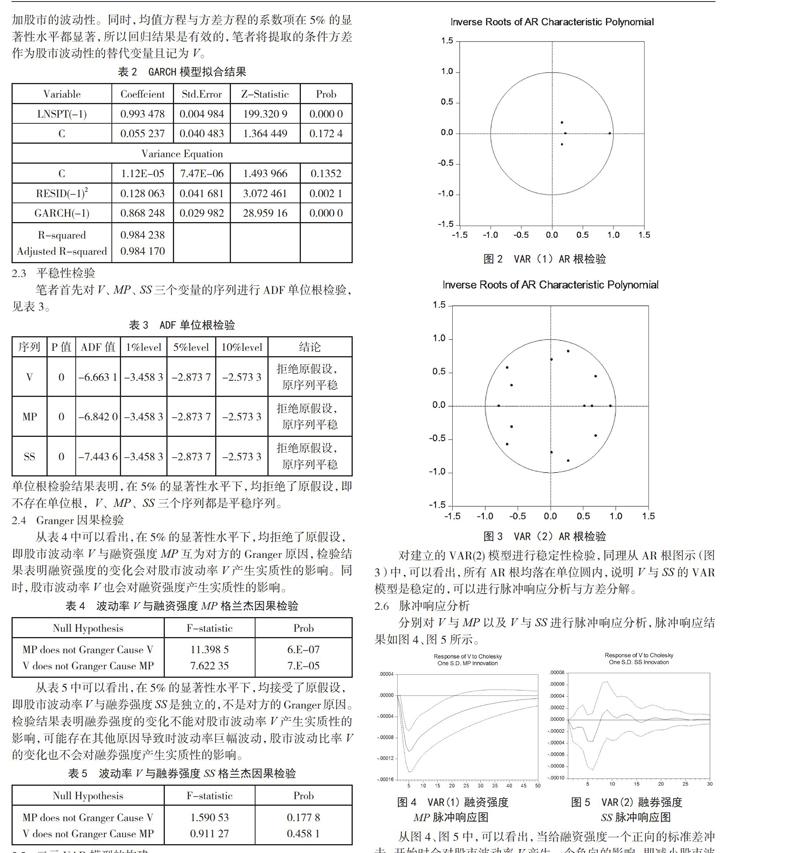
本文选取的数据是上证A股每日的收盘指数以及每日的融资融券数据，时间跨度是2014年10月21日至2015年9月30日，总共235个样本数据。

本文选取T-GARCH模型拟合股市波动，并选取条件方差作为股市波动的替代指标。同时计算并引入融资融券强度（看多看空系数）作为解释变量，两个变量的值域在-1～1之间，依次记为MP、SS。其中融资融券强度计算公式如下。

融资强度=（融资买入额-融资偿还额）/（融资买入额+融资偿还额）；融券强度=（融券卖出量-融券偿还量）/（融券卖出量+融券偿还量）。

2.2 ARCH效应检验

首先对上证A股指数波动性进行ARCH效应检验。为了减少量纲对实证分析的影响，笔者对收益率进行对数化处理，并记为lnspt。

回归结构中，R2（拟合优度）接近于1，说明该回归方程拟合效果较好，系数项与常数项在10%显著性水平下拒绝了原假设。

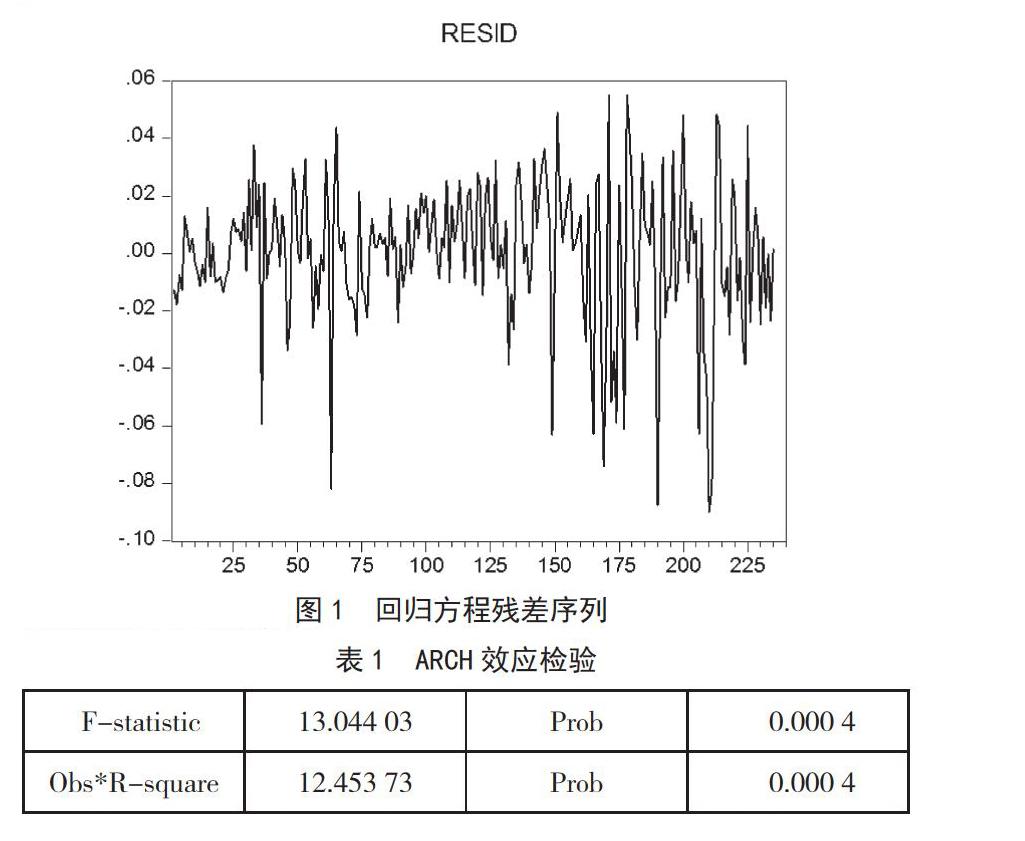
从回归方程的残差序列图（图1）中，发现波动出现乐波动集聚的现象，这说明该序列存在条件异方差性。因此，笔者对残差序列进行ARCH效应检验，并依据AIC准则来确定检验的阶数。通过上述操作，发现在1阶时，AIC值最小且为-10.629 86，因此确定检验阶数为1。

从表1中可以看出，在5%显著性水平下，拒绝原假设，即存在ARCH效应，因此，可以采用GARCH模型对这一时段的上证A股指数波动性进行拟合。

从表2中可以看出，回归方程的R2接近于1，拟合程度较好，非对称项的系数为正值，说明存在杠杆效应，且这种杠杆效应会增加股市的波动性。同时，均值方程与方差方程的系数项在5%的显著性水平都显著，所以回归结果是有效的，笔者将提取的条件方差作为股市波动性的替代变量且记为V。

从表5中可以看出，在5%的显著性水平下，均接受了原假设，即股市波动率V与融券强度SS是独立的，不是对方的Granger原因。检验结果表明融券强度的变化不能对股市波动率V产生实质性的影响，可能存在其他原因导致时波动率巨幅波动，股市波动比率V的变化也不会对融券强度产生实质性的影响。

2.5 二元VAR模型的构建

笔者分别确定了V与MP以及V与SS的最优滞后阶数，在进行脉冲响应分析以及方差分解之前，要首先验证构建的VAR模型是否稳定，检验标准是所有AR根均落在单位圆内。在此将V与MP的二元VAR模型定义为VAR（1），将V与SS的二元VAR模型定义为VAR（2）。

对建立的VAR（1）模型进行稳定性检验，从AR根图示（图2）中，可以看出，所有AR根均落在单位圆内，说明V与MP的VAR模型是稳定的，可以进行脉冲响应分析与方差分解。

对建立的VAR（2）模型进行稳定性检验，同理从AR根图示（图3）中，可以看出，所有AR根均落在单位圆内，说明V与SS的VAR模型是稳定的，可以进行脉冲响应分析与方差分解。

2.6 脉冲响应分析

分别对V与MP以及V与SS进行脉冲响应分析，脉冲响应结果如图4、图5所示。

从图4、图5中，可以看出，当给融资强度一个正向的标准差冲击，开始时会对股市波动率V产生一个负向的影响，即减小股市波动，这种影响在第5期时达到最大，随着期数的增加，这种影响在第50期逐渐消失。结果说明融资强度在这一时段的变化会减小股市的波动，而且这种影响不是持久的，随着时间的推移会逐渐减小直至消失。当给融券强度一个正向的标准差的冲击，开始时会对股市波动率V产生一个负向的影响，即减小股市波动，这种影响在第7期时达到最大，随着时间的推移，效应逐渐减弱直至消失。

2.7 方差分解

在VAR模型基础之上进行方差分解，获知融资融券强度对股市波动率V的解释能力。见表7、表8。

从表7可以看出，股市波动率V只有大约66.5%被其自身解释，而相当一部分被融资强度解释掉了，且融资强度解释股市波动的能力随着期数不断增加，在第20期时达到33.5%。从方差分解的结果来看，股市的巨幅波动与融资交易有着密不可分的联系，融资强度的变化对股市波动产生的影响是非常明显的。股市波动率V的大部分被其自身解释掉了，仅有小部分被融券强度解释。从表8中发现，融券强度对股市波动率的解释能力随着期数的增加也在增强，在第20期时达到1.454%。方差分解结果表明在股市巨幅波动阶段，融券强度的变化对股市波动存在一定的影响，但这种影响微乎其微。

2.8 “股灾”巨幅波动期的实证结果分析

第一，我国投资者结构严重不合理，机构投资者占比很小，而个人投资者的比重则非常大，投资策略主要是以投机需求为驱动，追求短期利益，也就是短线投资。大多数投资者缺乏投资理性，易产生跟风和踩踏效应，倾向化严重，容易对股指造成助涨杀跌的作用，极易造成股市的波动。

第二，多空双方规模悬殊，我国鼓励买多不买空。融资融券的规模始终无法平衡，融资的规模要远远超过融券的规模，由此导致券商等金融投资机构无券可融。这种规模的失衡带来的后果便是股市一旦有暴涨，则必有暴跌。

第三，我国融资融券交易机制不完善，法律法规与部门监管仍存在很大缺陷。比如：最明显的便是对于配资公司监管的不到位，只要中小投资者有一定的本金，在支付一定佣金费的情况下，就可以加数倍杠杆融资买入，而对于配资公司的审查及监管方面处于空白，因此便造成了杠杆的无度使用。

3 完善融资融券制度的建议

3.1 优化投资者结构

我国投资者结构目前主要呈现出机构投资者少，而个人投资者较多的情形，也就意味着证券市场主要以短线投资为主，也就是投机需求主导。尤其在股市大幅上扬时期，中小股民出于投机心理进行短线投资，不断加杠杆融资买入，是造成股市巨幅波动的主要原因之一。为了保证资本市场持续健康有效运行，更好地发挥对我国经济的助推作用，优化投资者结构势在必行，主张价值投资，长期投资，积极培育更为成熟的机构投资者与个人投资者。

3.2 建立有效的保证金制度

证券公司在融资融券日常交易的过程中实施“逐日盯市”制度，在实际操作中，分析证券信用交易的保证金追缴点具有如下重要意义：投资者可以据此判断自己可能承担的风险水平以及最大的损失程度；证券公司可以据此对没有追加担保物的投资者采取强制平仓措施，以保证其融资融券债权得以实现；而对于监管机构来说，根据不同的市场状况设定不同的维持保证比例，可以控制整个证券市场的信用程度和风险水平。

3.3 扩大融资融券标的范围

由于我国融资融券交易引入时间不长，融资融券标的股占A股市场的比例依然较低，还有很大的上升空间。融资融券标的规模小、种类少，不能很好地满足投资者的需求，不利于融资融券业务的展开，也就无法优化资源配置。因此，应该拓宽证券公司的经营范围，增加标的股数量及种类，提高证券市场的灵活性，满足不同层次投资者的需求。

主要参考文献

[1]F Allen，D Gale.Arbitrage， Short Sales， and Financial Innovation[J]. Econometrica，1991（4）.

[2]陈潇，杨恩.中美股市杠杆效应与波动溢出效应——基于GARCH模型的实证分析[J].財经科学，2011（4）.

[3]廖士光，杨朝军.卖空交易机制对股价的影响——来自台湾股市的经验证据[J].金融研究，2005（10）.