基于泰勒展开边界元法的近水面潜艇垂向二阶波浪力(矩)计算

段文洋, 王隶加, 陈纪康, 赵彬彬

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

基于泰勒展开边界元法的近水面潜艇垂向二阶波浪力(矩)计算

段文洋, 王隶加, 陈纪康, 赵彬彬

(哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001)

针对潜艇在近水面航行难以定深控制问题，利用一阶泰勒展开边界元方法求解切向诱导速度精度高的优势对其垂向二阶波浪力(矩)研究。该方法对边界积分方程中的偶极强度进行泰勒展开并保留至一阶导数项，同时在格林第三公式中关于场点沿边界取切向导数封闭方程组，直接求解出速度势及其沿物面的切向速度。计算迎浪状态下椭球体的垂向二阶波浪力(矩)，与现有成果吻合度较高；进而计算迎浪状态下潜艇模型的垂向二阶波浪力(矩)。数值计算结果表明：该方法有较高的计算精度且收敛速度快。

泰勒展开边界元法；垂向二阶波浪载荷；潜艇；频域；切向诱导速度

潜艇在近水面航行，有时需要保持定深以完成指定任务。文献[1]表明：垂向平面内的二阶波浪力(矩)会使潜艇逐渐向波面上浮，不利于定深控制和操纵。特别是在迎浪状态下，二阶波浪力表现为升力，将潜艇推向水面，甚至出现“抛甩”现象；此外还使潜艇产生纵倾，甚至艉部出水，对螺旋桨的性能造成影响。因此，有必要对近水面潜艇的垂向二阶波浪力(矩)展开研究。

缪国平等[2]用切片法将二阶波浪力从二维拓展到三维，计算潜体在不同潜深和浪向角时二阶垂向波浪力的变化趋势。林青山等[3]利用二阶波浪力切片理论对潜艇二阶纵倾力矩等进行了考察，并分析了指挥台、艉舵等对整条潜艇的影响。冯学知等[4]利用STF流体动力切片理论和Frank源相结合的方法对近水面潜体在波浪力作用下的运动响应建模并计算，表明二阶波浪力对潜体在垂向平面内的上浮起主要作用。冯学知等[5]基于细长体假设，结合三维修正系数，计算不同潜深和浪向下的运动响应和二阶波浪力(矩)。虽然切片法广泛应用于潜艇受力和运动预报，但本质上仍基于二维理论，对艇体首尾带来的影响值得商榷；而通过三维修正系数虽然能够满足工程要求，但该方法对不同模型的适用性需要验证。

Lee等[6]利用三维面元法对迎浪状态下椭球体的一阶波浪力(矩)和二阶波浪力(矩)进行数值计算，并与细长体理论比较。结果表明：随着面元数量增加，二阶垂向波浪力(矩)计算收敛极慢。虽然利用三维分布源频域方法可以求解二阶波浪力，但基于低阶分布源面元法求解二阶波浪力收敛较差，尤其是对非光滑边界物体，切向诱导速度误差极大[7]。针对该困难，段文洋[8]提出了泰勒展开边界元方法(taylor expansion boundary element method，TEBEM)的思想，即对源-偶混合分布方法中偶极强度进行一阶泰勒展开。其中，偶极切向变化恰好是切向速度，该方法对尖角处诱导速度有很好的模拟。Duan等[9-11]又将该方法展开至二阶，处理绕射辐射等问题，证明了泰勒展开边界元法能够有效地提高非光滑边界处切向诱导速度的计算精度。

本文基于一阶泰勒展开边界元方法，对近水面潜艇二阶定常波浪力(矩)进行计算，考虑该方法对潜艇计算的适应性。

1 近水面潜体二阶波浪力的定解问题

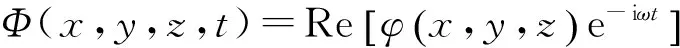
通常将空间速度势分解为入射势和扰动势两部分，即φ=φ0+φP。其中，入射速度势的表达式为

(1)

式中：A、ω、k0分别表示入射波浪的波幅、圆频率、波数，β表示入射波的传播方向与x轴正向之间的夹角(浪向角)，g表示重力加速度。

根据叠加原理，扰动势可分解为7个组成部分：

(2)

式中：vj为潜体6个自由度的运动速度，φj表示由于物体单位运动引起的辐射势，φ7为绕射势。

扰动速度势φj(j=1,2，…,7)的定解条件为

(3)

式中：D表示流域；n表示物面法向，由流体域指向潜体内部；SH表示潜体平均湿表面。

根据所求得的速度势和速度，利用近场公式沿潜体表面进行积分，可以得到作用在潜体上的一阶和二阶平均波浪力(矩)：

(4)

(5)

(6)

(7)

2 一阶泰勒展开边界元方法

传统基于源-偶混合分布的低阶面元法以各网格面元中点速度势作为整个面元速度势。利用无限水深三维频域无航速格林函数可以得到潜体平均湿表面上的速度势边界积分方程[1]，即：

(8)

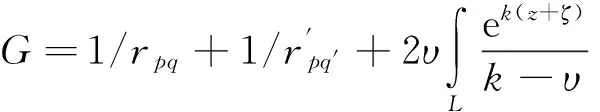
(9)

为了构建封闭方程组，对一阶TEBEM方法进行补充。在面元所在的局部坐标系下作垂直于法向的平面，并在该平面内取两个相互正交方向对场点求一阶导数。得到以下方程组：

(10)

将式(9)代入到式(8)、(10)中联立，并将积分边界SH离散为N个面元，可以得到一阶TEBEM方法的离散格式。对于任意面元i可以得到如下离散方程组，i=1,2,…,N：

(11)

式中：i和j表示面元编号；k= 1, 2, 3；m=1,2, 3。详细推导见文献[9-11]。

3 水下椭球体的结果与比较

为了验证TEBEM方法对于求解二阶波浪力(矩)的准确性，本文与Lee等[6]利用常数元方法计算的水下椭球体数值结果进行对比。

该算例假定长轴L与短轴D之比L/D=10的零航速椭球回转体在迎浪状态下重心位于静水面(0,0,-D)处，计算不同波浪频率下受到的波浪力(矩)。

图1～4分别表示利用一阶TEBEM方法在不同频率下计算的一阶垂荡波浪力、一阶纵摇波浪力矩、二阶垂向波浪力和二阶纵倾波浪力矩。

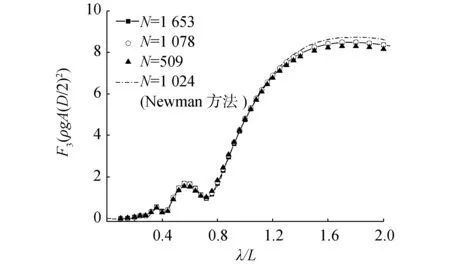
图1 椭球体一阶垂荡波浪力Fig.1 First-order heave force of submerged spheroid

图2 椭球体一阶纵摇波浪力矩Fig.2 First-order pitch moment of submerged spheroid

图3 椭球体二阶垂向波浪力Fig.3 Vertical drift force of submerged spheroid

图4 椭球体二阶纵倾波浪力矩Fig.4 Pitch drift moment of submerged spheroid

图1和图2分别给出了不同面元数下得到的一阶波浪力(矩)的计算结果，为了便于比较，利用ρgA(D/2)2和ρgA(D/2)3作无因次化处理，将结果与Newman利用三维面元法(面元数为1 024)得到的结果对比。从图中可以看出，一阶TEBEM方法得到的计算结果具有较好的收敛性；与Newman的结果比较，两者的主要差别集中在长波阶段，但误差均控制在3%以内。

图3和图4分别给出了不同面元数下的二阶垂向波浪力和二阶纵倾波浪力矩，并利用ρgA2(D/2)和ρgA2(D/2)2作无因次化处理。由于Newman利用三维面元法计算的二阶波浪力(矩)并没有达到收敛，故而将其所有面元数的计算结果全部比较。容易得出，利用一阶TEBEM方法求得的二阶波浪力(矩)具有较好的收敛性；并且除了中长波段(0.4<λ/L<1.2)以外，利用一阶TEBEM方法的结果与Newman 1 024网格数的结果基本一致。

4 潜艇波浪力计算实例

由上述第3节计算结果可知，基于一阶TEBEM方法能够得到令人满意的计算结果。本节以国外某一公开潜艇模型[12]为例，与上一节进行类似内容的计算。

由于并未查阅到有关该模型重心位置、惯性系数等潜艇模型参数，本节主要参考实际潜艇，估计相关参数。由于缺少该潜艇模型在无拘束状态下的波浪力计算相关文献，本节计算迎浪状态下，不同网格数的一阶波浪力(矩)和二阶波浪力(矩)。表1给出了潜艇模型的主要参数，图5给出了潜艇模型表面网格划分示意图。

表1 潜艇模型主要参数

图6和图7给出了不同面元数下一阶垂荡力和一阶纵摇力矩关于波浪频率的计算结果，并分别利用ρgA(D/2)2和ρgA(D/2)3作无因次化处理。

图5 潜艇模型表面网格划分Fig.5 The mesh on the submarine model surface

图6 Fr=0时，潜艇一阶垂荡波浪力Fig.6 First-order heave force of submarine as Fr=0

图7 Fr=0时，潜艇一阶纵摇波浪力矩Fig.7 First-order pitch moment of submarine as Fr=0

从图6和图7可以看出，一阶垂荡波浪力和一阶纵摇波浪力矩利用1 000左右网格数就能得到收敛结果。

图8 Fr=0时，潜艇二阶垂向波浪力Fig.8 Vertical drift force of submarine as Fr=0

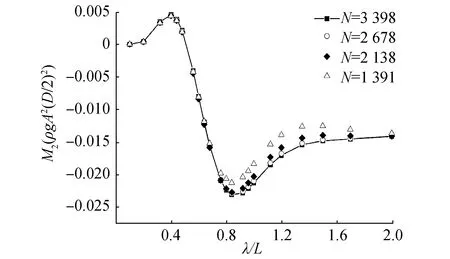
图9 Fr=0时，潜艇二阶纵倾波浪力矩Fig.9 Pitch drift moment of submarine as Fr=0

图8和图9给出了在相同工况下，二阶垂向波浪力和二阶纵倾波浪力矩的计算结果。从图中可以看出，二阶垂向波浪力的计算结果很快得到收敛，而二阶纵倾波浪力矩的计算结果收敛较慢。同时，二阶垂向波浪力和二阶纵倾波浪力矩在长波段的数值结果也能在一定程度上反映潜艇在垂直面内的上浮甚至“抛甩”的现象。

5 结论

本文在频域范畴内利用泰勒展开边界元方法计算潜艇一阶和二阶垂向波浪力和波浪力矩。以无限水深下近水面的椭球体和潜艇模型来验证一阶TEBEM方法的计算精度和收敛性。结论如下：

1)通过与椭球体的计算结果对比，证明一阶TEBEM方法具有较高的计算精度和收敛性。

2)采用一阶TEBEM方法对潜艇的波浪力(矩)计算：面元数1 000左右可以得到一阶垂荡波浪力和一阶纵摇波浪力的收敛结果，面元数2 000左右可以得到二阶垂向波浪力的收敛结果，二阶纵倾波浪力矩则需要3 000左右的面元数。

[1]戴遗山, 段文洋. 船舶在波浪中运动的势流理论[M]. 北京: 国防工业出版社, 2008: 78-84, 107-113. DAI Yishan, DUAN Wenyang. Potential flow theory of ship motions in waves[M]. Beijing: National Defense Industry Press, 2008: 78-84, 107-113.

[2]缪国平, 刘应中, 糜振星. 二阶波浪力的切片理论与潜体上的垂向定常力[J]. 水动力学研究与进展, 1993, 8(4): 435-447. MIAO Guoping, LIU Yingzhong, MI Zhenxing. A strip theory for the second-order wave forces and the steady vertical forces on submerged slender bodies[J]. Journal of hydrodynamics, 1993, 8(4): 435-447.

[3]林青山, 缪国平, 李谊乐, 等. 潜艇上二阶波浪力的考察[J]. 船舶力学, 1998, 2(6): 15-23. LIN Qingshan, MIAO Guoping, LI Yile, et al. On the second-order wave forces on submarines[J]. Journal of ship mechanics, 1998, 2(6): 15-23.

[4]冯学知, 缪泉明, 蒋强强. 近水面波浪力作用下潜体的非线性运动响应[J]. 中国造船, 1996(3): 29-35. FENG Xuezhi, MIAO Quanming, JIANG Qiangqiang. Prediction of nonlinear motion responses of a submerged slender body running near free-surface due to wave-exciting forces[J]. Shipbuilding of China, 1996(3): 29-35.

[5]冯学知, 蒋强强, 缪泉明, 等. 潜体波浪中近水面不同潜深和航向时运动和波浪力计算[J]. 船舶力学, 2002, 6(2): 1-14. FENG Xuezhi, JIANG Qiangqiang, MIAO Quanming, et al. Computation of motion and wave forces for a submarine running near free surface in different depth of immersion and direction[J]. Journal of ship mechanics, 2002, 6(2): 1-14.

[6]LEE C H, NEWMAN J N. First and second order wave effects on a submerged spheroid[J]. Journal of ship research, 1991, 35(3): 183-190.

[7]徐刚, 段文洋. 常数分布Rankine源法与二阶绕射问题精度研究[J]. 哈尔滨工程大学学报, 2010, 31(9): 1144-1152. XU Gang, DUAN Wenyang. Numerical investigation of second-order wave diffraction based on the Rankine source method[J]. Journal of Harbin Engineering University, 2010, 31(9): 1144-1152.

[8]DUAN Wenyang. Taylor expansion boundary element method for floating body hydrodynamics[C]//Proceedings of the 27th International Workshop on Water Waves and Floating Bodies. Copenhagen, Denmark, 2012.

[9]段文洋, 陈纪康, 赵彬彬. 基于泰勒展开边界元法的深水浮体二阶平均漂移力计算[J]. 哈尔滨工程大学学报, 2015, 36(3): 302-306. DUAN Wenyang, CHEN Jikang, ZHAO Binbin. Calculation of second-order mean drift loads for the deepwater floating body based on the Taylor expansion boundary element method[J]. Journal of Harbin Engineering University, 2015, 36(3): 302-306.

[10]DUAN Wenyang, CHEN Jikang, ZHAO Binbin. Second-order Taylor expansion boundary element method for the second-order wave diffraction problem[J]. Engineering Analysis with Boundary Elements, 2015, 58: 140-150.

[11]DUAN Wenyang, CHEN Jikang, ZHAO Binbin. Second-order Taylor expansion boundary element method for the second-order wave radiation problem[J]. Applied Ocean Research, 2015, 52: 12-26.

[12]GROVES N C, HUANG T T, CHANG M S. Geometric characteristics of DARPA SUBOFF models (DTRC model Nos. 5470 and 5471). DTRC/SHD-1298-01[R]. Bethesda, Maryland: David Taylor Research Centre, 1989.

Calculation of vertical second-order drift loads on a submarine floating near the free water surface based on Taylor expansion boundary element method

DUAN Wenyang，WANG Lijia，CHEN Jikang，ZHAO Binbin

(College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)

A submarine traveling near the free water surface experiences difficulty in depth control. Thus, the vertical second-order mean force and moment acting on the submarine were studied. One-order Taylor expansion boundary element method (TEBEM) is used to improve the solution accuracy of the tangential induced velocity.This method keeps the first-order derivative for the dipole strength of the border integral equation and then takes the two tangential derivatives with respect to the field points on the boundary to form the closed equations in the third formula of the Green function. The velocity potential and the tangential induced velocity along object surface can be solved directly. This method was applied to calculate the vertical second-order drift loads of a submerged spheroid in head seas. The results show good agreement with previous numerical solutions. The vertical second-order drift loads of a submarine model were also calculated. TEBEM was found to achieve higher accuracy and quick convergence.

Taylor expansion boundary element method; second-order vertical drift force; second-order pitch drift moment; submarine; frequency-domain; tangential induced velocity

2016-06-11.

时间：2016-12-12.

国家自然科学基金资助项目(11272097).

段文洋(1967-),男,教授,博士生导师； 陈纪康(1986-),男,博士后.

陈纪康,E-mail: cjkhrb@sina.com.

10.11990/jheu.201606032

O352

A

1006-7043(2017)01-0008-05

段文洋, 王隶加, 陈纪康,等. 基于泰勒展开边界元法的近水面潜艇垂向二阶波浪力(矩)计算[J]. 哈尔滨工程大学学报， 2017, 38(1): 8-12. DUAN Wenyang，WANG Lijia，CHEN Jikang，et al. Calculation of vertical second-order drift loads on a submarine floating near the free water surface based on Taylor expansion boundary element method[J]. Journal of Harbin Engineering University, 2017, 38(1): 8-12.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20161212.0920.008.html