基于传输线方程的多根非平行传输线串扰分析

刘鑫+钟选明+叶志红+廖成

摘 要： 非平行结构的传输线在电力电子系统中普遍存在，当其上通有电压和电流信号时，会在周围传输线上产生串扰响应。采用时域传输线方程建立多根非平行传输线之间的串扰模型，结合FDTD方法，分析在脉冲集总源激励下受扰导线始端和终端负载上的串扰电压响应特性，将其结果与仿真结果对比，验证了该方法的正确性。研究结果表明，非平行结构中受扰线始端和终端负载上的串扰电压响应随着传输线离地面高度的增大而增大，随着传输线之间夹角的增大而变小，且减小的趋势逐渐减弱，从而为线缆间的串扰防护提供了参考依据。

关键词： 非平行传输线； 时域传输线方程； 串扰响应； FDTD

中图分类号： TN811?34 文献标识码： A 文章编号： 1004?373X（2017）01?0163?04

Abstract： The transmission line with non?parallel structure is prevalent in the power electronic system， and the crosstalk response will be produced around it when the voltage and current signals are transmitted through it. The time?domain transmission line equation is used to establish the crosstalk model among the multiconductor non?parallel transmission lines. The FDTD method is combined to analyze the crosstalk voltage response characteristics of the disturbed conductor beginning and terminal loads under the pulse lumping source excitation. The results are contrasted with the simulation results to verify the validity of the method. The research results show that the crosstalk voltage response of the disturbed conductor beginning and terminal loads in non?parallel structure is increased with the height increasing of the transmission line， decreased with the included angle increasing between the transmission lines， and the decrease trend is decayed gradually， which provides a reference for the crosstalk protection among cables.

Keywords： non?parallel transmission line； time?domain transmission line equation； crosstalk response； FDTD

0 引 言

在电气设备、电子仪器中，由于内部连接传输线较多，线与线之间常常是密集且以非平行结构分布排列的，这样就导致导线之间容易产生串扰现象，从而使设备遭受影响，导致性能降低或功能不正常。文献[1]指出传输线间的串扰是电器工程中常见的电磁干扰模式。因此在电磁兼容问题上，对传输线间的串扰问题进行研究显得尤为重要。

当非平行传输线上通有电压和电流信号时，会在其周围产生电磁场，从而在其他传输线上产生串扰响应，影响传输线两端设备的正常工作。国内外在传输线串扰问题的计算方法和特性分析上也做了一定研究。文献[2?6]对多导体传输线在时域和频域上的串扰分析做了大量研究，例如文献[7]分析了单导体传输线与屏蔽电缆的串扰问题，文献[8]则基于BLT（Baum?Liu?Tesche）方程对线缆网络的电磁干扰响应进行求解，但其分析和计算的对象都是平行结构的传输线，对于非平行结构的传输线则没有涉及。而文献[9]中则采用频域BLT方程，离散传输线并引入理想节点的概念计算非平行传输线间的串扰响应，文献[10]采用阶梯式均匀传输线模型，对非平行传输线进行分段逼近，文献[11]利用基于Daubechies小波函数的MRTD方法计算非平行微带线间的夹角对串扰的影响。

目前对非平行结构的传输线研究，文献中多采用基于BLT方程的频域算法分析传输线的串扰问题，但频域BLT方程涉及大量矩阵运算，且计算相对复杂。本文将时域传输线方程和FDTD方法结合起来，采用传输线方程建立非平行导体的串扰模型，利用FDTD的差分格式对传输线方程进行离散，计算在集总激励源下的受扰线始端和终端负载的时域串扰电压，同时分析了非平行传输线结构的串扰特性。

1 传输线模型

结合传输线方程将非平行传输线进行离散，把每一个离散线段近似地看作是平行结构，从而求得非平行结构传输线的串扰电压响应。

1.1 非平行传输线模型

考虑如图1（a）所示的情况，为平行于地面且相互不平行的两条传输线，分别为离地面的高度，和分别为两传输线之间的距离和夹角，传输线的始端接有激励源其内阻为终端接负载传输线的两端分别接有负载和为干扰线，为受扰线。

把传输线离散成段，每段按照平行的结构进行分析处理，计算出每段的分布参数，最后根据传输线方程的差分格式求得非平行传输线的串扰电压响应。

2 计算结果

通过使用商业仿真软件对非平行结构传输线的算例进行模拟，验证了本文提出方法的正确性，并在此基础上分析了非平行传输线之间以及离地高度对串扰电压的影响。

2.1 算法正确性验证

如图1（a）所示，选取半径0.001 m，夹角为5°的非平行传输线0.15 m，0.150 57 m且与参考坐标平行，离地高度均为0.01 m，0.01 m， Ω， Ω。采用双指数脉冲作为激励源，如图3所示。

非平行传输线在双指数脉冲激励下，受扰线近端和远端的电压响应曲线如图4所示。其中虚线表示使用FDTD程序计算的结果，实线表示在同一计算模型下，使用商业软件仿真的结果。从图中可以看出两种方法的计算结果基本吻合，从而验证了本文非平行传输线串扰计算方法的正确性。

2.2 夹角对非平行传输线串扰特性的影响

如图5所示，干扰线和受扰线参数不变，且处于同一平面内，分别计算非平行双线夹角为5°，15°，30°和45°四种情况下受扰线始端和终端的串扰电压。从图5中可以看出： =15°时比=5°时串扰电压减少约7 mV，=30°时比=15°时串扰电压减少约3.5 mV，=45°时比=30°时串扰电压减少2 mV。随着夹角角度的增加，线间串扰电压呈现明显的减小趋势，但减小的趋势逐渐减弱。这是因为当夹角增大时，受扰线与干扰线之间的整体距离是增加的，传输线之间的耦合减小，这也说明传输线间的夹角对电磁干扰的影响很大。

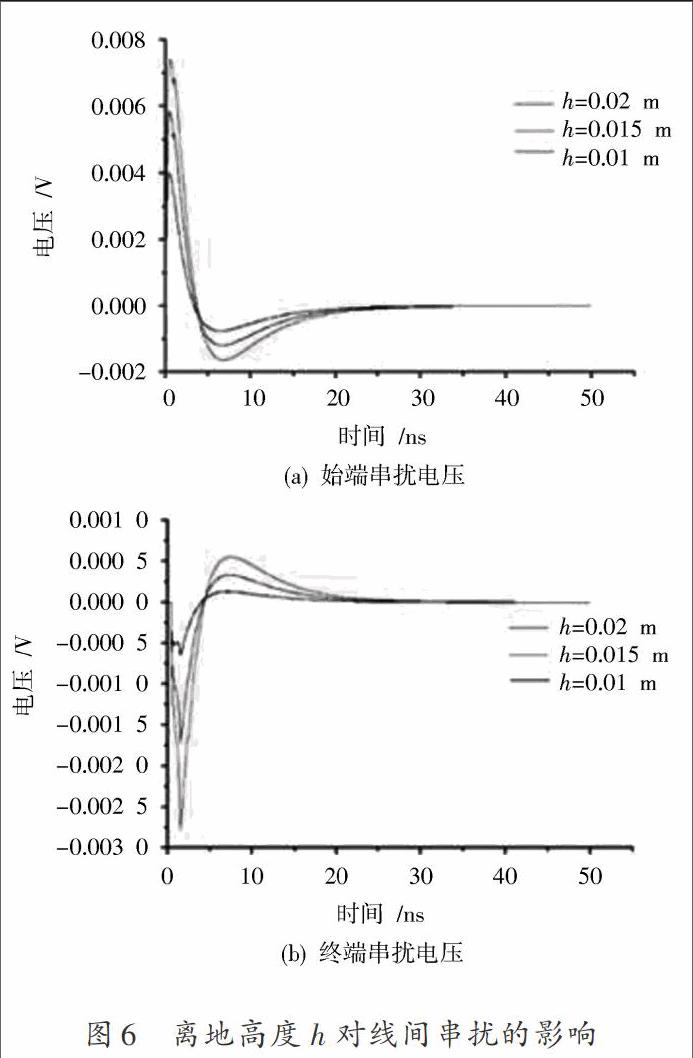
2.3 离地高度对非平行传输线串扰特性的影响

如图6所示，在干扰线和受扰线参数不变，两传输线间夹角为45°的情况下，传输线距离地面的高度分别为0.01 m，0.015 m，0.02 m，求得受扰线始端和终端的串扰电压，由图6可知，传输线距离地面越高，始端和终端的串扰电压越大，这是由于随着高度的增大，使得传输线上每一离散段的自电感和互电感增加所造成的。

3 结 语

本文采用时域传输线方程建立了非平行傳输线的串扰模型，采用FDTD的差分格式对传输线方程进行离散，得到了在脉冲集总激励源下受扰线始端和终端负载上的串扰电压响应。通过商业仿真软件对非平行传输线串扰模型的数值模拟，验证了本文提出算法的正确性，同时，分析了非平行传输线的串扰特性。结果表明两线间夹角越大，串扰电压越小，且减小的趋势逐渐减弱；两线离地高度越高，串扰电压越大。为研究复杂电磁环境下的电子系统电磁干扰问题提供了一定的理论依据。

参考文献

[1] 叶烽，党松.电磁兼容性技术的内涵及其发展[J].现代电子技术，2001，24（1）：65?69.

[2] OMID M， KAMI Y， HAYAKAWA M. Field coupling to non?uniform and uniform transmission lines [J]. IEEE transactions on EMC， 1997， 39（3）： 201?211.

[3] PAUL C R. Analysis of multiconductor transmission lines [M]. New York： Wiley， 1994： 223?312.

[4] CELOZZI S， FELIZIANI M. Time?domain solution of field excited multiconductor transmission line equations [J]. IEEE transactions on EMC， 1995， 37（3）： 421?431.

[5] PAUL C R. Literal solutions for the time?domain response of a two?conductor transmission line excited by an incident electromagnetic field [J]. IEEE transactions on EMC， 1995， 37（2）： 241?251.

[6] 张志军.电磁脉冲对传输线耦合规律的研究[D].北京：华北电力大学，2006.

[7] 周大瑜，廖成，叶志红，等.屏蔽腔体中多导体传输线串扰抑制的仿真研究[J].现代电子技术，2015，38（8）：148?150.

[8] 高雪莲，张晓宇，赵磊，等.基于BLT方程的复杂线缆网络电磁干扰响应求解[J].科学技术与工程，2015（5）：248?252.

[9] 覃宇建，周东明，何建国.BLT方程在任意布局传输线串扰分析中的应用[J].国防科技大学学报，2009，31（2）：55?58.

[10] 张友文，刘光斌.非均匀传输线间的串扰研究[J].微波学报，2011（4）：85?87.

[11] 权赫，孙兆牛.抑制非平行微带线间串扰的保护带方法研究[J].电子测量与仪器学报，2011（10）：850?856.