基于DFT及谐波群泄露能量最小的电力谐波/间谐波分析方法

慕昆+马小雨+何国锋

摘 要： DFT在电力系统谐波分析中得到广泛应用，但是非整周期采样会导致频谱泄露、混叠及栅栏效应。基于能量守恒原理，当整周期采样时能量主要集中在主频上，泄露很小。IEC61000?4?7对群谐波均方根值（RMS）做了定义，因此采用增加或减少采样点数并递归运用DFT的方法，计算基波群谐波的泄露能量并使其最小，可达到最接近整周期采样的效果，通过DFT可直接得到各次谐波信息。数值仿真结果表明该方法可准确计算基波及谐波频率、幅值和相位，在信号存在白噪声时依然有效。

关键词： 谐波分析； 递归DFT； 泄露能量最小； 频谱泄露

中图分类号： TN911.6?34； TP273 文献标识码： A 文章编号： 1004?373X（2017）01?0111?04

Abstract： The discrete Fourier transform （DFT） is widely used in the harmonic analysis of the power system， in which the non?complete?period sampling will lead to the spectrum leakage， aliasing and picket?fence effect. On the basis of energy conservation principle， when the energy of the complete period is focused on the main frequency， the leakage will be small. The RMS of group harmonic was defined by IEC61000?4?7. The method of using the variety of sampling points and recursive DFT is adop?ted to calculate the leakage energy of the fundamental?wave group harmonic and make it to the minimum， and obtain the sampling effect nearest to the complete period. The information of each harmonic is obtained by means of DFT. The numerical simulation results show that the method can calculate the fundamental wave， harmonic frequency， amplitude and phase accurately， and is still effective while the white noise exiting in the signal.

Keywords： harmonic analysis； recursive DFT； least leakage energy； spectrum leakage

0 引 言

随着电力电子技术的发展，各种非线性负载的加入使电力系统收到谐波、间谐波污染。如何在有限长的采样窗口长度下准确提取信号中各频率成分，有利于对谐波和间谐波污染进行进一步评估。

谐波分析的方法有很多种，由于离散傅里叶变换（Discrete Fourier Transform，DFT）具有算法成熟，易于DSP工程实现，成为分析谐波和间谐波的最常用工具。但是由于采样数据长度和采样的非同步化，产生了频谱泄漏和栅栏效应[1]，各频率成分之间还会产生频谱干扰，影响分析效果。针对上述问题，国内外学者进行了大量研究，提出了多种改进措施。

在时域，若采样对于信号中各成分都是同步的，那么理论上DFT/FFT计算结果不存在误差。文献[2]通过采样长度的自适应计算使信号各成分与采样窗口近似同步，再用DFT计算各谐波、间谐波参数。若信号基频已知，则可通过多项式插值对信号重采样使采样对谐波同步，但对间谐波而言，频谱泄漏依然存在。在频域，解决栅栏效应的方法有线性调频Z变换的频谱细化法[3]、补零法[4]和各种插值法[5?10]。前两种方法对信号DFT值的进一步密化，并未考虑信号各成分间的频谱干扰。插值法通过插值求得信号各成分实际频率与对应离散频点的偏差解决栅栏效应，其抑制频谱干扰的手段为时域加窗。

本文在国际标准[11?12]谐波子群定义的基础上给出了一种基于递归DFT的谐波分析方法，该方法通过检测谐波子群的最小泄露能量值来获得近似的整周期采样，从而得到谐波信息。

1 IEC谐波检测标准

IEC61000?4?7：2008标准[11]规定了实际供电系统中电流和电压谐波和间谐波测量仪器的架构。测量仪器的结构由主要部分和后续处理部分组成。检测仪器主要部分包括：带有抗混叠滤波器的输入回路、具有采样/保持单元的模/数转换器、同步和窗口单元（如需要）、DFT处理器。

新的IEC标准推荐采用加矩形窗的DFT算法。为满足标准测量要求，窗口宽度应选为10个（50 Hz系统）或12个（60 Hz系统）周期。同时，时间窗应与电力系统50 Hz（60 Hz）频率对应的10（12）个周期同步。

新标准定义谐波群的有效值为：某一个谐波有效值以及它邻近频谱分量有效值的方和根，如式（1）和图1所示（只考虑50 Hz系统）。

当信号中为稳态的基波和谐波，且采样为同步采样（同步误差在 IEC标准要求范围内）时，通过DFT单频谱谱线可以较精确地估计信号的基波或各次谐波分量。

当信号含幅值波动的基波和（或）谐波时，波动的基波和谐波分量会将其能量扩散到邻近的间谐波频率分量中去。这时可以利用IEC方法的谐波群或谐波子群参数估计基波和谐波，但该方法不能提供相位信息。

IEC 方法对间谐波测量问题做了很大的简化，采用间谐波群和间谐波子群估计间谐波，即用两个连续谐波频率之间的 DFT 频谱谱线估计频率之间的所有间谐波，不给出间谐波的具体频率和相位。

2 谐波群有效值最小方法

式中：离散频率的谐波幅值为。由于频谱泄露，频率的能量会泄露到周围的频域内，因此周围总的谐波能量构成了“群能量”[12]，每一个群能量包含频段内的能量这里为整数，表示群的宽度。这样每次谐波幅值可表示为。由DFT可知，主要的频谱泄露集中在主谐波周围，这样间谐波（子谐波）可以识别出来。

以采样频率对电力信号（电压和电流）进行点采样，对这点采样值进行DFT运算，DFT运算后，主频频谱密度幅值最大，幅值在主频的左右两侧逐渐衰减，次大的频谱出现在紧邻主频左右两侧位置。基于经验观察，当信号过采样时，主频右侧幅值大于左侧幅值，即；相反的信号欠采样时，主频右侧幅值小于左侧幅值即。这样，根据分散能量的情形适当调整采样窗的宽度使之满足接近整周期采样，则可消除得到接近整周期采样的采样数据，然后进行DFT即可得到很少泄露的频谱分析。

该能量仅是扩散到基波周围的能量，不包括基波能量。根据能量守恒定理，时域能量等于频域能量，又由采样定理可知当信号被整周期采样时，频谱不会发生泄露，全部集中在主频上，泄露能量基本为零。因此根据频谱幅值的大小调整采样窗宽度，使之接近满足整周期采样，则可得到极小的能量泄露。当时过采样，可减少一个采样点；当时欠采样，可增加一个采样点，该过程重复进行直到泄露能量最小时停止。

该过程如下：

（1） 设定采样频率，对信号进行10周期采样；

（2） 对采样信号进行DFT，找出幅值最大点处的频率

（3） 如果，。反之，进行下一步；

（4） 如果，。反之，进行下一步；

（5） 判断分散能量是否满足如果满足停止迭代，确定此时值；反之返回第（2）步，重复该过程直到

（6） 由點采样值可确定基波频率、幅值及相角以及谐波频率、幅值及相角

（7） 如果有间谐波，则采用频域插值方法获得间谐波信息。

当进行DFT时，由于频谱泄露，第次谐波能量可扩展到周围很宽的频带内，但是每一组群谐波能量必须在和范围内进行计算。如果频带越宽，泄露能量越接近真实值。但是频带宽度增加后可能会包含临近谐波引起的泄露，另外，由于临近谐波成分的影响，较宽的带宽会引起计算频率偏离实际频率，因此为了获得准确的幅值希望选取较大的而为了避免混叠希望较小的宽度。基于IEC标准频带宽度可选取5个。

另外，最小能量是该算法停止迭代的一个关键因素，理论上为了获得准确结果，最小能量越小越好，但是迭代次数增加，为了降低运算时间，最小能量可选为1‰倍的基波幅值。

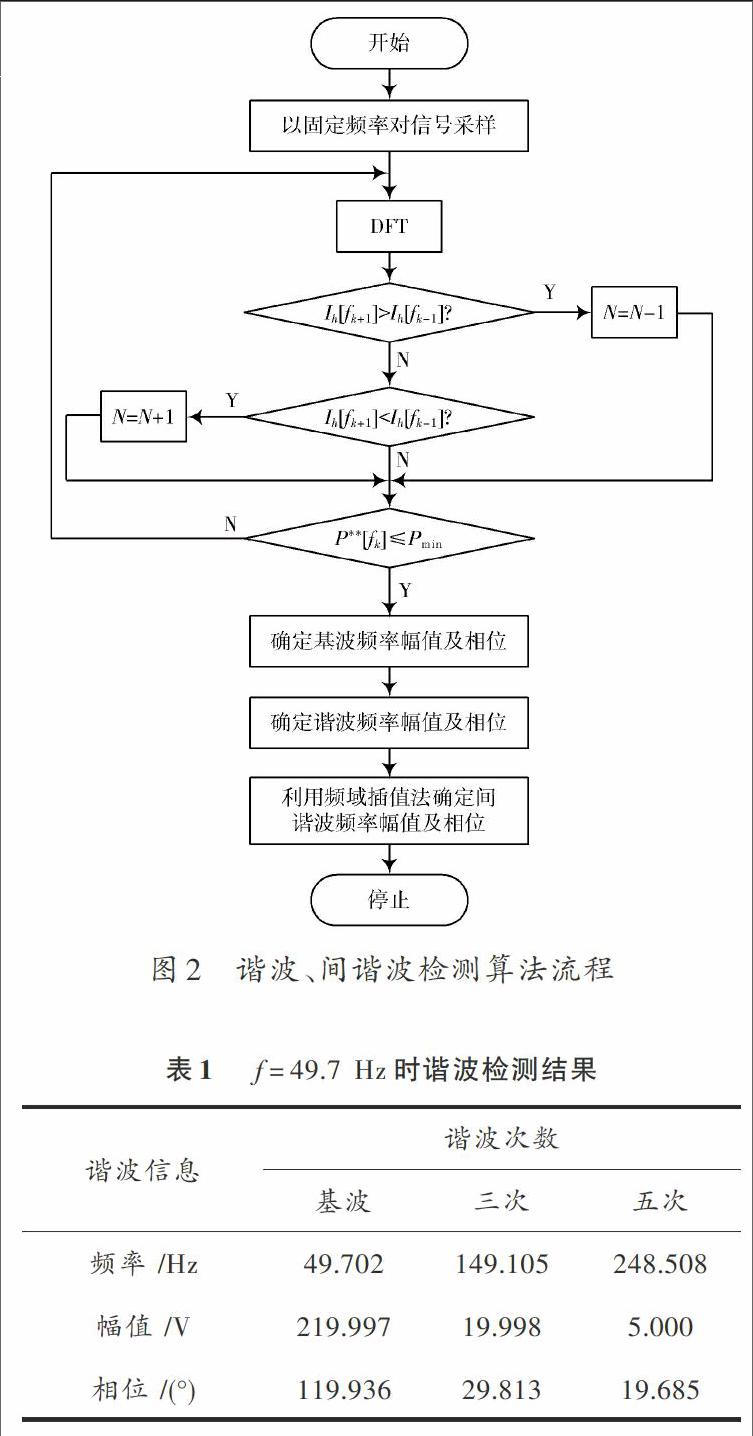
该算法的流程图如图2所示，当基波群谐波RMS最小时，对应泄露能量最小，表明基本没有出现能量泄露，采样基本达到整周期采样。此时DFT分析结果为整周期采样结果，基波及各次谐波频率、幅值及相位都可以由DFT输出直接得到，且基本接近真实值。如果检测到间谐波，由于间谐波不可能是整周期采样，肯定发生频谱泄露，因此可以采用频域插值的方法得到间谐波的幅值、频率及相位信息。

3 数值仿真

为验证该方法的有效性，分别选取含谐波正弦信号及间谐波信号进行仿真。

（1） 谐波信号

假设输入信号为：

式中：为相对于基波40 dB的白噪声；基波频率。基于上述的分析方法对该信号进行仿真，经过6次迭代，得到的结果如表1所示，从表1中的数据可以看出，采用这种递归的方法可以很准确地测量出各次谐波信息。

该例中，基波频率为相比上例，添加了93.5 Hz的间谐波信号。谐波分析按照泄露能量最小的方法进行仿真，由于间谐波无法采用该方法计算，可以利用Hanning窗插值函数[7]对间谐波进行计算，仿真结果如表2所示。

从表2中的数据可以看出，由于间谐波的原因，临近的三次谐波的仿真结果相比表1结果误差更大，但是误差还是在合理的范围内。

从两种仿真结果可以看出，基于谐波群泄露能量最小的方法能够准确检测出各次谐波的频率、幅值和相位信息，对于间谐波则采用频域插值的方法也可得到较为满意的结果。

4 结 论

整周期采样时DFT不会发生频谱泄露，可准确测量基波及谐波参数。基于IEC标准定义的谐波均方根值，通过增加或减少采样点数，递归使用FFT算法，使其达到最小，则可以得到接近于整周期的采样效果。仿真实验验证了该方法能够准确地计量各次谐波频率、幅值及相位。该方法只需递归调用DFT，便于植入基于微处理器的电力系统监控设备中。

参考文献

[1] 张伏生，耿中行，葛耀中.电力系统谐波分析的高精度FFT算法[J].中国电机工程学报，1999，19（3）：63?66.

[2] 王彭，周峰，黄震宇，等.基于时域准同步的谐波和间谐波检测算法[J].仪器仪表学报，2013，34（2）：275?280.

[3] 王楠，肖先勇，曾颂崎，等.基于插值线性调频Z变换的间谐波分析方法[J].电网技术，2007，31（18）：43?47.

[4] 陈华丽，陆怀恩，曾云，等.一种提高谐波测量精度的新算法[J].继电器，2003，31（3）：40?43.

[5] 潘文，钱俞寿，周鹗.基于加窗差值FFT的电力谐波测量理论（II）双插值FFT理论[J].电工技术学报，1994，9（2）：53?56.

[6] 赵文春，马伟明，胡安.电机测试中谐波分析的高精度FFT算法[J].中国电机工程学报，2001，21（12）：83?87.

[7] 庞浩，李东霞，俎云霄，等.应用FFT进行电力系统谐波分析的改进算法[J].中国电机工程学报，2003，23（6）：50?54.

[8] AGREZ D. Weighted multipoint interpolated DFTF to improve amplitude estimation of multi?frequency signal [J]. IEEE tran?sactions on instrumentation and measurement， 2002， 51（2）： 289?292.

[9] 黄方能，黄成军，陈陈，等.高精度插值FFT谐波分析[J].电力自动化设备，2007，27（9）：40?42.

[10] LANGLOIS P， BERGERON R. Interharmonic analysis by a frequency interpolation method [C]// Proceedings of 1992 2nd International Conference on Power Quality. Atlanta： IEEE， 1992： 1231?1237.

[11] 祁才君，王小海.基于插值FFT算法的间谐波参数估计[J].电工技术学报，2003，18（1）：92?95.

[12] 钱昊，赵荣祥.基于插值FFT算法的间谐波分析[J].中国电机工程学报，2005，25（21）：87?91.

[13] Standards Policy and Strategy Committee. Electromagnetic compatibility （EMC）， part 4?7： testing and measurement techniques?general guide on harmonics and inter?harmonics measurements and instrumentation， for power supply systems and equipment connected thereto： IEC 61000?4?7： 2008 [S]. London： Standards Policy and Strategy Committee， 2008.

[14] 侯立峰，黄纯，李波，等.基于中国国家标准和IEC标准的谐波及间谐波测量方法[J].电网技术，2010，34（8）：46?51.