基于粒子群算法优化的车辆主动悬架PID控制

赵强，白欣

(东北林业大学 交通学院，哈尔滨 150040)

基于粒子群算法优化的车辆主动悬架PID控制

赵强，白欣

(东北林业大学 交通学院，哈尔滨 150040)

针对汽车主动悬架PID控制器的参数选择问题，采用粒子群优化方法优化PID控制器的控制参数。以汽车行驶平顺性作为评价指标，建立综合车身垂直加速度、悬架动行程和轮胎动载荷3项指标的目标函数，采用粒子群算法优化控制器参数。在MATLAB软件中进行仿真。结果显示：经过粒子群优化后的PID控制器性能明显优于优化前性能。

主动悬架；粒子群算法；PID控制

0 引言

汽车悬架是汽车的重要总成之一，人们为了提高它的性能，在不断地研究，从而出现了主动悬架，使得悬架的运动可以得到控制，从而提高车辆行驶平顺性和乘坐舒适性。

主动悬架的控制方法有很多种，其中PID控制是最为普遍了一种方式，人们对其研究已持续近百年，提出了多种求解参数方法及改进方法[1]。针对PID控制器参数的确定，有Ziegler-Nichols方法[2]、Cohen-Coon响应曲线方法[3]等传统方法均是通过经验公式计算求得，其具有一定的鲁棒性，但只能适用于满足经验公式条件的对象，且只利用了较少的系统动态特性信息，使所得到的控制器性能局限。随着智能技术的发展与应用，出现了神经网络法、遗传算法、基于规则的整定方法等智能方法，它们都具有很大的灵活性，并且可以灵活地运用专家知识和经验，使控制器的适用范围扩大，减小局限性，但他们还是有各自不足之处。例如遗传算法寻优的速度慢，且很难提高等。粒子群算法是近年来兴起的一种群体智能优化算法，具有结构简单、收敛速度快、设置参数少、容易实现等优点，能有效地解决复杂优化问题[4]。本文采用此算法对PID参数进行优化，搜索在一定车辆参数时PID的最优参数。通过建模仿真，对比优化前后得到的数据，验证优化的有效性。

1 系统模型的建立

为了方便研究，本文采用简化的二自由度1/4主动悬架模型，如图1所示。

参照图1模型，根据牛顿第二定律建立主动悬架的动力学微分方程：

式中：ms为车身质量；mu为轮胎质量；cs为阻尼系数；ks为弹簧刚度；ku为轮胎刚度；xs为车身位移；xu为轮胎位移；x0为路面位移；u为控制器力。

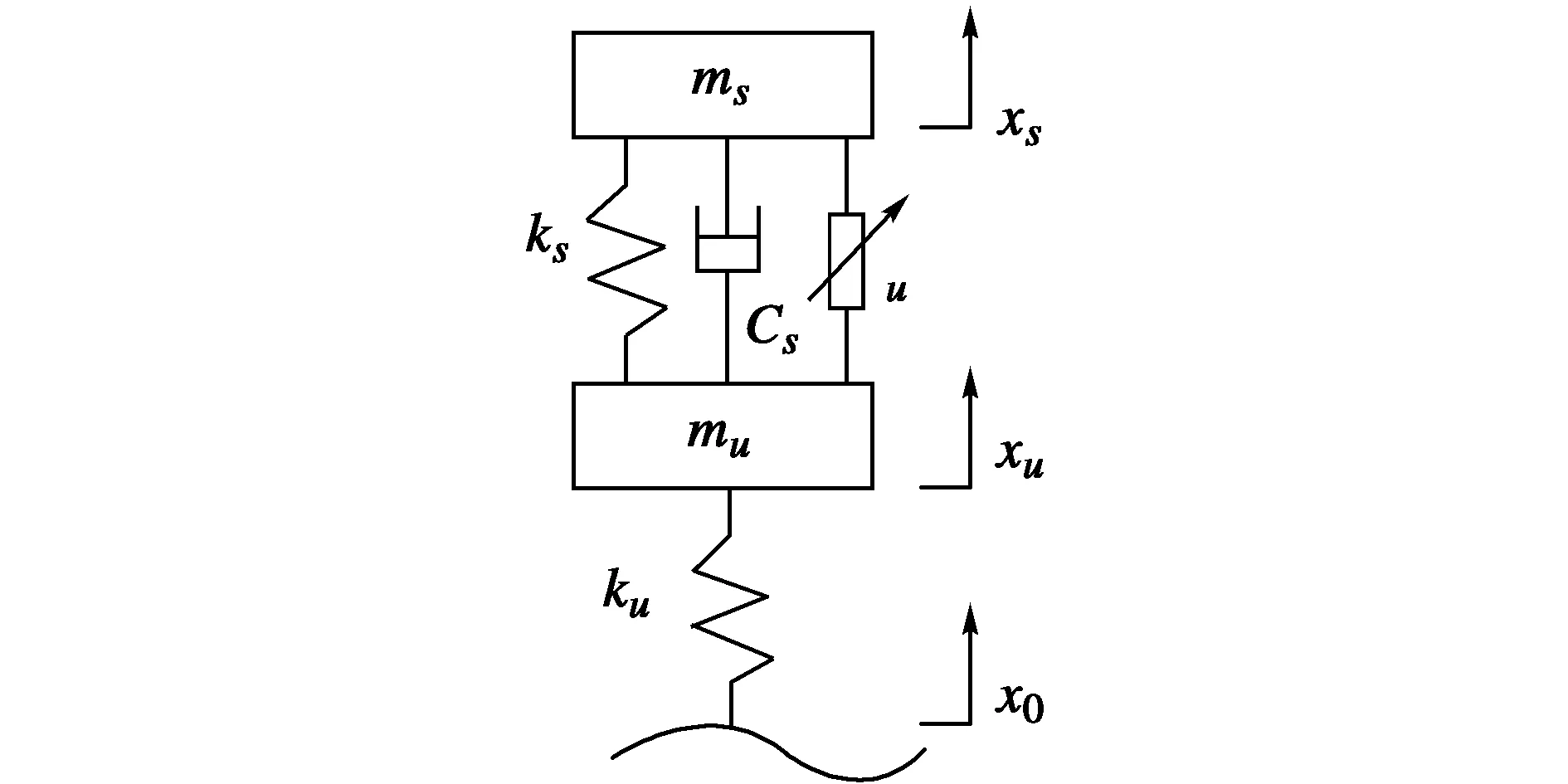
图1 1/4主动悬架模型Fig.1 1/4 active suspension model

采用滤波白噪声法得到路面时域激励模型为：

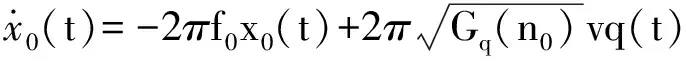
(3)

式中：f0为下截止频率；Gq(n0)为路面不平度系数；v为车辆速度；q(t)为数学期望为零的高斯白噪声；w为频率指数；n为空间频率；n0为参考空间频率。

2 PID控制器

悬架的PID控制系统包括控制器和悬架两个部分，其框图如图2所示。

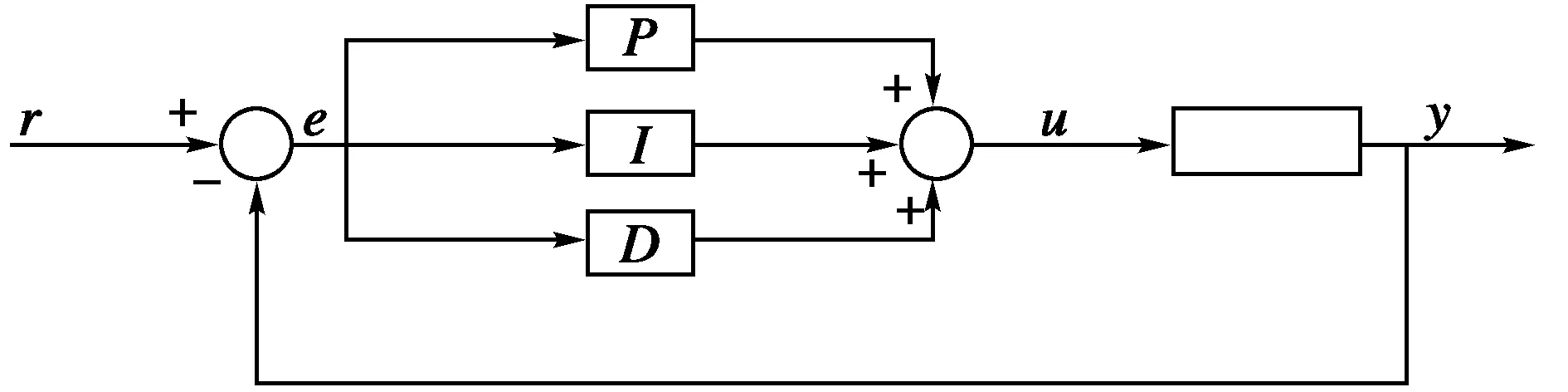
图2 PID调节器框图Fig.2 Block diagram of PID regulator

PID控制器是一种线性控制器，它的输入量是给定的信号与实际得到的输出信号的偏差，对偏差分别进行比例、积分和微分三种运算，将三种运算结果相加即为控制器的最终结果，PID控制器的算法表达如下：

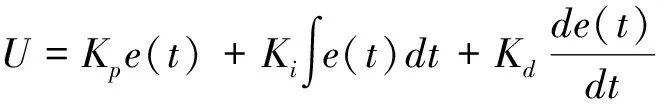
(4)

式中：e(t)为偏差信号，e(t)=r(t)-y(t)；r(t)为输入信号；y(t)为被控对象的输出；Kp为比例系数；Ki为积分系数；Kd为微分系数。

研究发现：Kp增大，调节时间越快，但Kp过大，则容易产生超调；积分环节作用是静态误差，其系数Ki越大，积分作用越弱；微分环节通过引入早期修正信号，加快系统响应速度。以上三个系数比较难调，采用试凑等方法很难得到最优值。

3 基于粒子群算法的PID参数优化

3.1 粒子群算法

粒子群算法是由Kennedy J和Eberhart R C在1995年提出的一种基于群体智能的随机优化算法，近年来已广泛应用于函数优化等领域[5]。

粒子群算法的原理：在一个D维目标搜索空间中，由n个微粒组成一个群体，其中每个微粒是一个D维的向量，其空间位置表示为xi=(xi1，xi2，…，xiD)，i=1，2，…n。微粒的空间位置是目标优化问题中的一个解，将其代入到相应的适应度函数中，可以算出适应度值，根据适应度值来衡量微粒的质量；微粒的飞行速度也是一个D维的向量，可以记为vi=(vi1，vi2，…，viD)；每个微粒经历过的适应值最大的位置称为个体最优解，可记为pi=(pi1，pi2，…，piD)；整个微粒群所经历过的最好位置称为全局最优解，可记为pg=(pg1，pg2，…，pgD)；粒子群的进化方程可描述为：

vij(t+1)=wvij(t)+c1r1(t)[pij(t)-xij(t)]+

c2r2(t)[pgj(t)-xij(t)]。

(5)

xij(t+1)=xij(t)+vij(t+1)。

(6)

式中：下标i表示微粒；下标j表示微粒的第j维；t表示第t代；r1～U(0，1)，r2～U(0，1)为两个相互独立的随机函数；c1，c2为加速常量，取值通常在(0，2)之间，c1用来调节微粒飞向自身最优解方向的步长，c2用来调节微粒飞向全局最优解方向的步长。

w为惯性权重，表示保留原来速度的程度。w较大时，全局收敛能力强，局部收敛能力弱，有利于算法跳出个体最优解；w较小，全局收敛能力弱，局部收敛能力强，有利于算法收敛。所以在计算中w初值应取较大，随着迭代的进行逐渐减小w值，所以可运用公式(7)的线性方法来对w值进行计算：

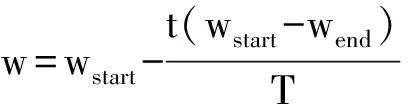
(7)

式中，wstart，wend分别表示惯性权重的初始值和迭代到最大次数时数值，t为当前迭代次数，T为最大迭代次数。

3.2 优化变量的约束条件确定和算法流程

3.2.1 目标函数选择

粒子群算法的优化变量为PID控制器的比例、积分及微分三个环节的系数。目标函数为含有车体质心垂直振动加速度、悬架动行程、轮胎动变形三个指标的函数。由于这三个指标的单位和数量级均不同，因此将其分别除以对应的被动悬架的性能指标即可得到优化的目标函数：

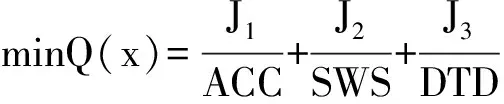
(8)

式中：Q(x)为目标函数；J1为主动悬架车体垂直加速度的均方根值；J2为主动悬架的悬架动行程的均方根值；J3为主动悬架轮胎动变形的均方根值；ACC为被动悬架车体质心垂直振动加速度的均方根值；SWS为被动悬架的悬架动挠度的均方根值；DTD为被动悬架轮胎动变形的均方根值。

3.2.2 适应度函数选择

适应度函数是来衡量粒子位置优劣的函数，其值越大，则粒子的位置越好，所以适应度函数应求得其最大值。而目标函数是求取最小值的问题，因此选取目标函数的倒数作为粒子群算法优化的适应度函数，如公式(9)所示。

(9)

综上所述，得到粒子群算法流程图如图3所示。

图3 粒子群算法的流程图Fig.3 Flow diagram of particle swarm optimization

4 仿真分析

4.1 主动悬架仿真

在MATLAB/Simulink软件中建立二自由度1/4车辆主动悬架仿真模型，其参数表1。

表1 悬架模型的参数

路面等级选B、C级路面，相应的Gq(n0)分别为64×10-6、265×10-6；下截止频率f0=0.1；车辆速度为v=20m/s；频率指数w=2。

4.2 粒子群优化仿真

利用粒子群算法对PID控制器的各个参数进行优化，优化参数的范围：Kp为[0，300]；Ki为[0，3]；Kd为[0，3]。算法参数设定如下：粒子群算法的群体规模为100；惯性权重初值为1，终值为0.5；最大迭代次数为100；速度更新参数都为2。目标函数为公式(8)，将主动悬架进行优化，并将优化前后的主动悬架以及被动悬架的仿真结果放在一起进行对比分析。

4.3 仿真结果分析

4.3.1 B级路面仿真及分析

将主动悬架模型用粒子群算法优化并进行仿真，得到目标函数的收敛曲线如图4所示。

图4 目标函数收敛曲线Fig.4 The convergence curve of the objective function

优化后目标函数值为2.725 2，对应的PID控制器参数：Kp为108.65；Ki为2.89；Kd为0.26。优化前通过试凑得到的各参数：Kp为100；Ki为1.0；Kd为1.0。将优化前后以及被动悬架的各指标放到一起进行对比，得到的1/4车身垂直加速度、悬架动行程、轮胎动载荷三个指标的仿真曲线如图5～7所示。并计算均方根值进行比较，结果见表2。

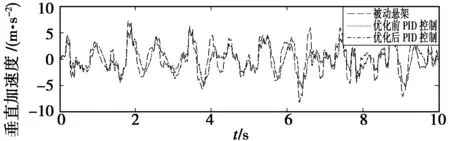
图5 1/4车身垂向加速度控制效果对比曲线Fig.5 Contrast curve of control effect of 1/4 body vertical acceleration

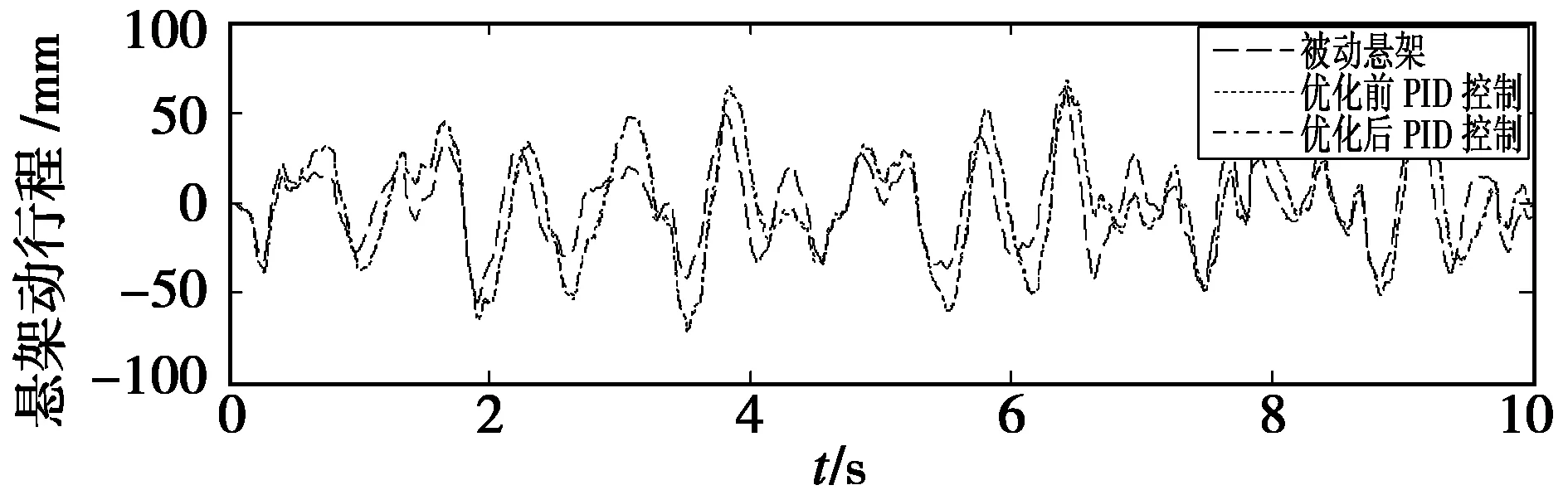
图6 悬架动行程控制效果对比曲线Fig.6 Contrast curve of control effect of suspension working space

图7 轮胎动载荷控制效果对比曲线Fig.7 Contrast curve of control effect of tire dynamic loads

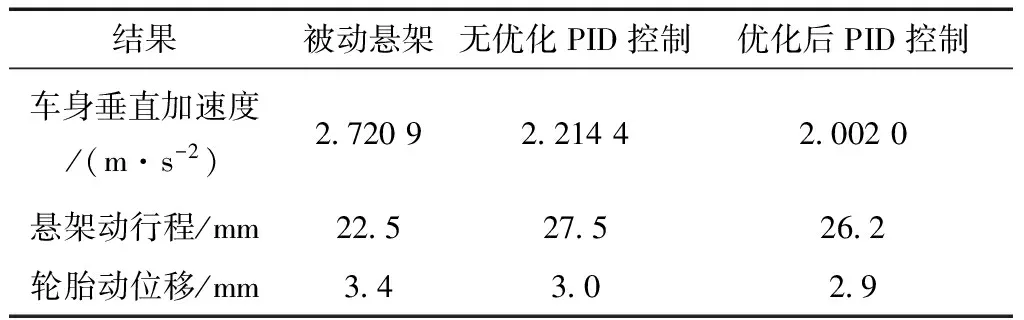
结果被动悬架无优化PID控制优化后PID控制车身垂直加速度/(m·s-2)272092214420020悬架动行程/mm225275262轮胎动位移/mm343029

由以上图表可以看出，经过粒子群算法优化后的PID控制器比优化前的控制器的控制效果在各方面都有提升。其中，1/4车体质心垂直振动加速度减少了9.6%，悬架动行程减少了4.7%，车轮动载荷减少了3.3%。

4.3.2 C级路面仿真及分析

将主动悬架模型用粒子群算法优化并进行仿真，得到目标函数的收敛曲线如图8所示。

优化后目标函数值为2.718 4，对应的PID控制器参数：Kp为108.38；Ki为2.04；Kd为0.015。优化前通过试凑得到的各参数：Kp为100；Ki为1.0；Kd为1.0。将优化前后以及被动悬架的各指标放到一起进行对比，得到的1/4车身垂直加速度、悬架动行程、轮胎动载荷三个指标的仿真曲线如图9～11所示。并计算均方根值进行比较，结果见表3。

图8 目标函数收敛曲线Fig.8 The convergence curve of the objective function

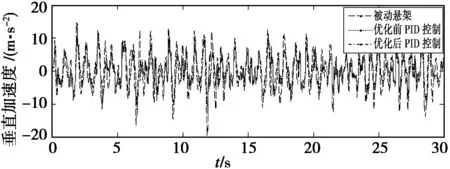
图9 1/4车身垂向加速度控制效果对比曲线Fig.9 Contrast curve of control effect of 1/4 body vertical acceleration

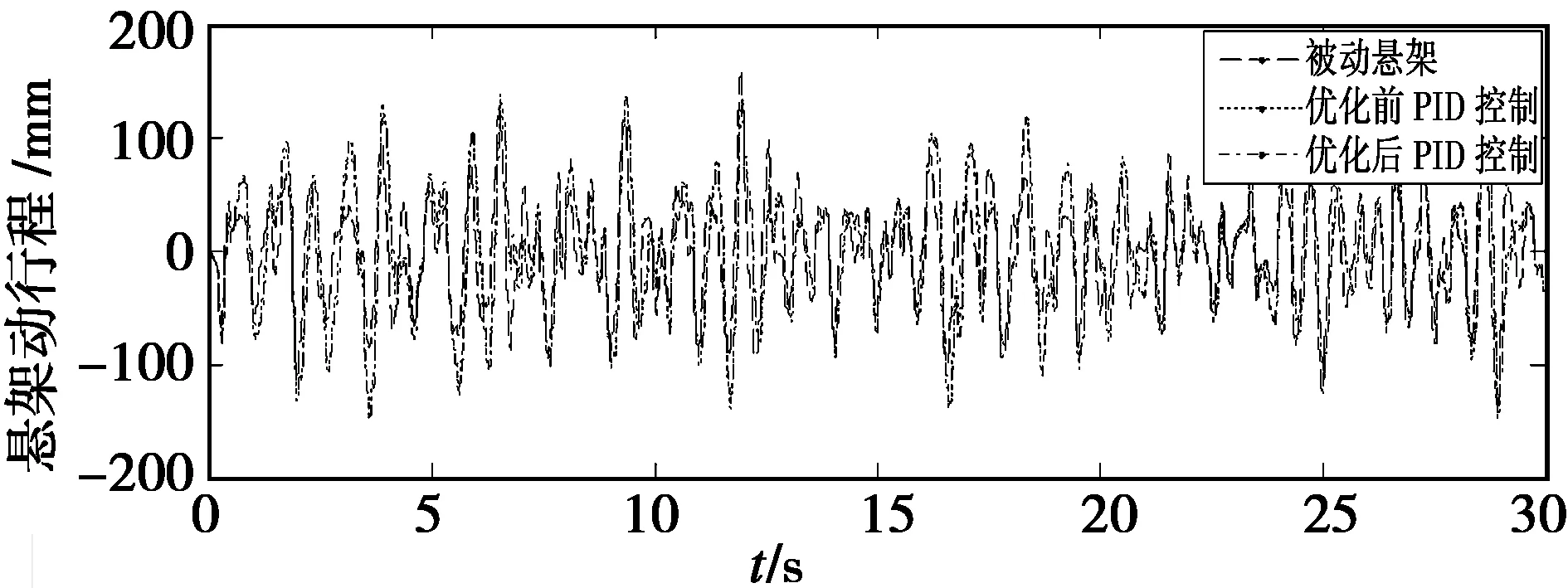
图10 悬架动行程控制效果对比曲线Fig.10 Contrast curve of control effect of suspension working space

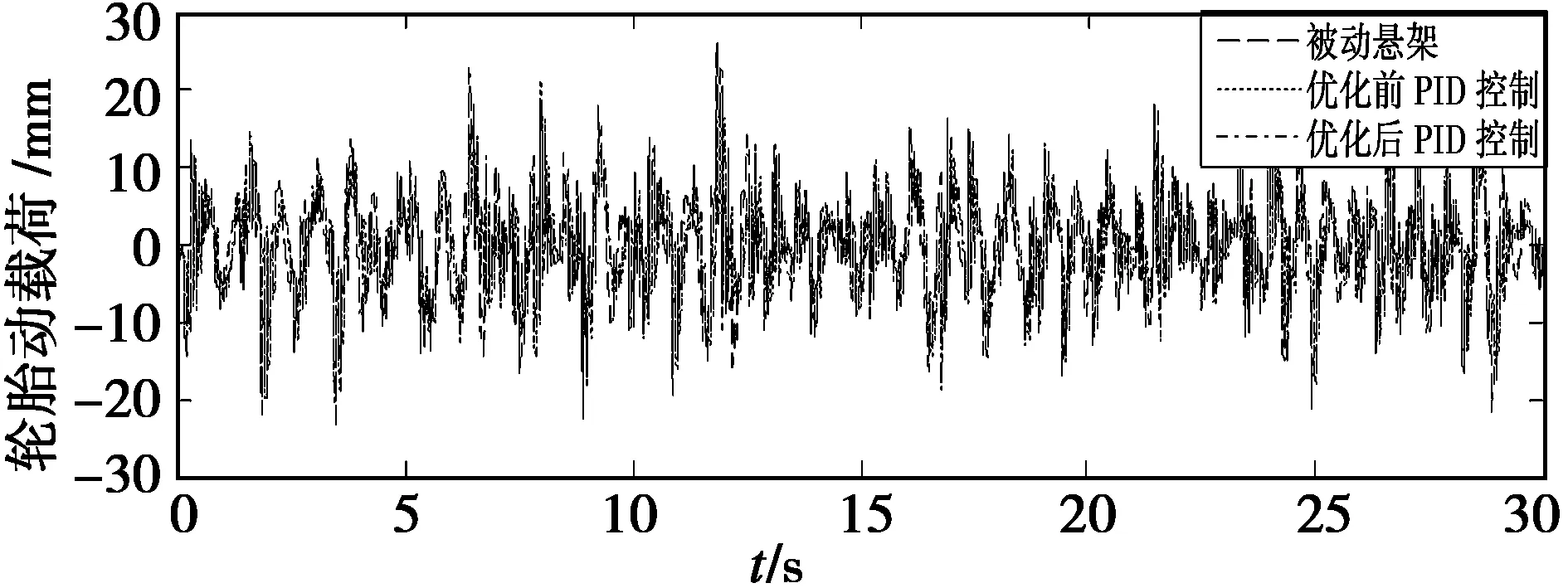
图11 轮胎动载荷控制效果对比曲线Fig.11 Contrast curve of control effect of tire dynamic loads

由以上图表可以看出，经过粒子群算法优化后的PID控制器比优化前的控制器的控制效果在各方面都有提升。其中，1/4车体质心垂直振动加速度减少了6.23%，悬架动行程减少了1.19%，车轮动载荷减少了4.95%。

表3 仿真结果的统计分析

5 结束语

建立了1/4主动悬架模型，分别在B级和C级路面上通过滤波噪声激励，采用粒子群算法优化PID控制器，对比优化前后的PID控制效果。结果表明，优化后的PID控制器能够有效改善振动中的车身加速度、轮胎动载荷和悬架动行程。由于PID控制的局限性和一定的单一性，使得其无法兼顾控制所有性能指标，但粒子群优化后的PID控制器，能有效地减小其局限性，在有效控制其主要目标的同时，使得其他指标得到一定的改善。

[1]王蕾，宋文忠.PID控制[J].自动化仪表，2004，25(4)：3-8.

[2]Ziegler J G.Optimum settings for automatic controllers[J].Transactions of the A.s.m.e，1942，115(2B)：759-768.

[3]Cohen G H，Coon G A.Theoretical consideration of retarded control[J].Transactions of the American Society of Mechanical Engineers，1953：433-444.

[4]刘道.基于改进粒子群优化算法的PID参数整定研究[D].衡阳：南华大学，2012.

[5]Kennedy J E，Eberhart R.Particle swarm optimization[C].In Proceedings of the IEEE International Conference on Neural Networks，Perth，Australia.1995(4)：1942-1948.

[6]赵强，丁柏群.用改进的粒子群算法求解并联6自由度平台的最大误差[J].机械设计，2007，26(6)：39-42.

[7]付涛，王大镇，弓清忠.车辆主动悬架优化设计与仿真分析[J].计算机工程与应用，2016，52(6)：253-257.

[8]梁军.粒子群算法在最优化问题中的研究[D].桂林：广西师范大学，2008.

[9]赵强，范超雄，孙子尧，等.车辆电液主动悬架PID最优控制研究[J].森林工程，2014，30(1)：68-72.

[10]钱凯.汽车行驶平顺性分析及粒子群算法在悬架优化中的应用[D].重庆：重庆交通大学，2013.

[11]詹长书，程崇.基于模糊自适应PID控制器的空气悬架控制策略研究[J].武汉理工大学学报(交通科学与工程版)，2015，39(5)：934-938.

[12]刘顺安.PSO-BP网络算法在汽车悬架优化中的应用[J].吉林大学学报(工学版)，2009，39(3)：571-575.

[13]Chiou J S，Tsai S H，Liu M T.A PSO-based adaptive fuzzy PID-controllers[J].Simulation Modelling Practice & Theory，2012，26(8)：49-59.

[14]Chiou J S，Wang K Y.Application of a hybrid controller to a mobile robot[J].Simulation Modelling Practice & Theory，2008，16(7)：783-795.

[15]何法，基于遗传算法优化的车辆主动悬架模糊PID控制[J].重庆理工大学学报(自然科学)，2016，30(2)：6-11.

[16]Lu S.Simulation of pavement roughness and IRI based on power spectral density[J].Mathematics and Computers in Simulation.2003，61(2)：77-88.

[17]Tandel A，Deshpande A R，Deshmukh S P，et al.Modeling，Analysis and PID controller implementation on double wishbone suspension using SimMechanics and Simulink[C].Procedia Engineering，2014，97：1274-1281.

PID Control of Vehicle Active Suspension Basedon Particle Swarm Optimization

Zhao Qiang，Bai Xin

(Traffic College，Northeast Forestry University，Harbin，150040，China.)

In order to solve the problem of optimal parameters selection for PID controller of vehicle active suspension，particle swarm optimization was used to optimize the control parameter of PID controller.Taking the smoothness of vehicle driving as the evaluation index，three objective function was established with respect to the body vertical acceleration，the suspension dynamic displacement and the tire dynamic loads.The particle swarm optimization was employed to conduct parameter optimization of the controller.MATLAB was used to complete the control simulation.The simulation results showed that the property of the optimized PID controller by the particle swarm optimization was obviously improved compared to the one without optimization.

active suspension；particle swarm optimization；PID controller

2016-07-07

黑龙江省留学归国人员科学基金(LC2015019)

赵强，博士，教授。研究方向：载运工具装备设计与功能创新。E-mail：qyangzhao@163.com

赵强，白欣.基于粒子群算法优化的车辆主动悬架PID控制[J].森林工程，2017，33(1)：66-69.

U 463

A

1001-005X(2017)01-0066-04