基于广义S变换的齿轮箱轴承故障诊断方法

陈换过 易永余 陈文华 陈 培 沈建洋浙江省机电产品可靠性技术研究重点实验室，杭州，310018

基于广义S变换的齿轮箱轴承故障诊断方法

陈换过 易永余 陈文华 陈 培 沈建洋
浙江省机电产品可靠性技术研究重点实验室，杭州，310018

齿轮箱轴承故障冲击信号通常具有非平稳和非线性的特点，若在强背景信号与噪声中，更加难以识别和提取。鉴于广义S变换具有良好的自适应性和时频聚集性，提出了一种基于广义S变换的齿轮箱滚动轴承故障诊断方法。对广义S变换的时窗函数进行讨论，分析了不同参数对调节窗函数宽度的影响；讨论了不同程度的轴承故障在广义S变换时频谱图上的能量分布；通过仿真和实验验证了所提方法的可行性。结果表明，广义S变换方法能有效地反映不同轴承故障的特征频率，为齿轮箱的轴承故障诊断提供一种有效的方法。

齿轮箱；广义S变换；故障诊断；滚动轴承

0 引言

滚动轴承故障是旋转机械的典型故障。滚动轴承元件工作表面发生局部损伤时，会产生突变的冲击脉冲力，该冲击信号的频率即为轴承故障特征频率。但由于旋转机械传动系统的复杂性以及工作条件的多样性，故而使轴承振动信号具有非平稳和非线性的特点，各种激励源产生的信号相互耦合，导致故障冲击特征常被淹没在强背景信号与噪声中而难以识别，尤其是轴承早期损伤的微弱冲击特征，更是不易提取[1]。若能从复杂信号中成功提取该冲击特征，则可方便有效地对滚动轴承相关故障进行诊断。

常用的时频分析方法有短时傅里叶变换、Gabor变换和小波变换等，时频分辨率是衡量这些方法优劣和时频聚集性能的重要指标。短时傅里叶变换和Gabor变换使用的都是大小固定的滑动窗口,不能精确分解周期比时间窗大的低频信号,并且高频的时频分辨率比较差。小波变换虽能自适应地反映低频和高频成分,但小波基函数一旦选定,分析所有数据都必须用此小波函数,将造成信号能量的泄漏,产生较多虚假谐波[2]。

S变换是由STOCKWELL等[3]在短时傅里叶变换和连续小波变换的基础上提出的信号处理方法。S变换是一种可逆的时频分析方法，它保持了信号的绝对相位信息，其时频分辨率随着频率发生变化。然而，由于S变换中采用的小波函数是固定的，因此缺乏自适应性。文献[4]中通过引入调节系数，将S变换进行扩展，提出了广义S变换。广义S变换可以根据分析信号的时频特征不同而自动地调节窗函数的宽度，以便达到最佳的时频分辨率，对非平稳信号中不同信号分量有着更强的区分能力。近些年来,广义S变换在地震信号处理[5]、电能质量扰动分析[6]中得到广泛应用，部分学者也对广义S变换应用于机械故障诊断领域作了深入研究。郭远晶等[7]利用S变换对低信噪比的滚动轴承故障信号进行处理，有效地从中提取出周期性的冲击特征。朱明等[8]利用广义S变换分析了滚动轴承故障冲击特征，结果表明广义S变换能有效地反映不同轴承故障的特征频率。YANG等[9]针对风电机组设计了基于S变换的状态监测与故障诊断系统，对振动信号进行监测，并通过模拟试验，验证了系统的可行性。ROOPA等[10]研究了基于S变换的离散余弦变换时频分析方法。

广义S变换具有自适应性的特点，但是调节参数对时窗函数影响较大。因此本文针对振动信号非平稳性特点，将广义S变换引入齿轮箱轴承故障诊断中，并讨论了不同的参数对调节窗函数宽度的影响；通过仿真分析和实验验证了所提方法的有效性，并讨论不同程度的轴承故障在广义S变换时频谱图上的能量分布，找到轴承故障和能量值的关系。

1 广义S变换原理

设函数h(t)∈L2(R)，L2(R) 表示能量有限函数空间，则信号h(t)的一维S变换定义为

(1)

式中，h(t)为时间序列；τ为时移因子；σ为尺度因子；f为频率;g(t)为高斯窗函数。

当σ=1/f时，有

S(τ,f)=

(2)

高斯窗函数g(t)取为

(3)

由上文可知，高斯窗的尺度因子与频率成反比关系，故低频处的频率分辨率较高，而高频处的时间分辨率较高。为了改变时频分辨率，在高斯窗的尺度因子中引入调节因子λa和p,改造S变换的高斯窗函数,进一步加快或减慢时窗宽度随信号频率变化的速度，更好地适应具体信号的分析。

令尺度因子为

(4)

将式(4)代入式(1),得到一维广义高斯S变换的表达式:

(5)

当λa=1,p=1时，广义S变换即变为标准的S变换。在实际应用中,对一维S变换的高斯窗函数进行改造,直接引入调节参数k：

σ=k/f

(6)

将式(6)代入S变换表达式中，得到广义S变换更一般的表达式：

(7)

此时，高斯窗函数g(τ,f)相应变为

(8)

(9)

一维广义S变换的具体算法流程如图1所示。

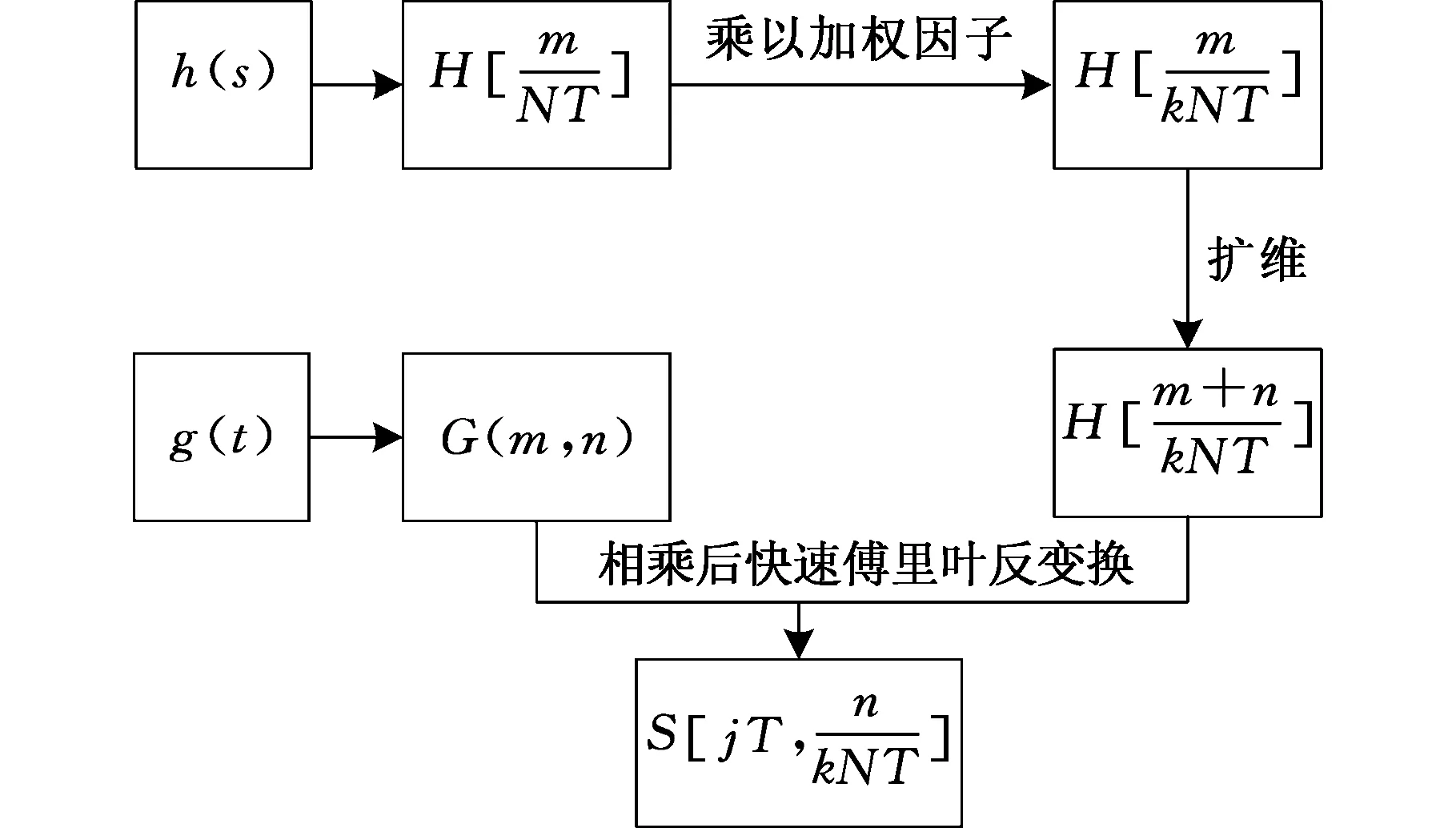
图1 一维广义S变换的算法流程图Fig.1 Flow chart of generalized S-transform

2 不同参数的广义S变换窗函数比较

由式(4)可知，尺寸因子的大小随着参数λa和参数p的变化而变化，选择合适的尺寸因子能进一步加快或减慢时窗宽度随信号频率变化的速度，更好地适应具体信号的分析。但在实际应用中，两个参数的变化会增加学习成本、降低效率，故将两个参数简化为一个调节参数k。由式(6)可知，尺寸因子的大小只受k的影响，故可以通过讨论不同k值下的广义S变换窗函数的特点，找出相对合适的k值取值范围，图2为不同k值的广义S变换窗函数频谱图。

由图2可知,当调节因子k增大时，窗函数的宽度会向外进行延拓，且相应窗函数的幅值变小；当调节因子k变小时，则窗函数的宽度向内收缩，相应窗函数的幅值变大。通过参数对比可知，k的调节对窗函数宽度和幅值均产生影响，可以根据实际应用的需要,合理地选择k值来自适应地调节广义S变换的窗函数宽度，且在一定的范围内，k的取值越大，广义S变换时频分辨率越高，能量聚集性越好。

3 轴承故障信号的广义S变换

当齿轮和轴承出现局部故障时，会产生突变的冲击脉冲力。为了验证广义S变换良好的时频聚焦性，模拟齿轮箱中轴承故障时所测得的非平稳信号x(t)进行仿真分析：

(a)k=0.3

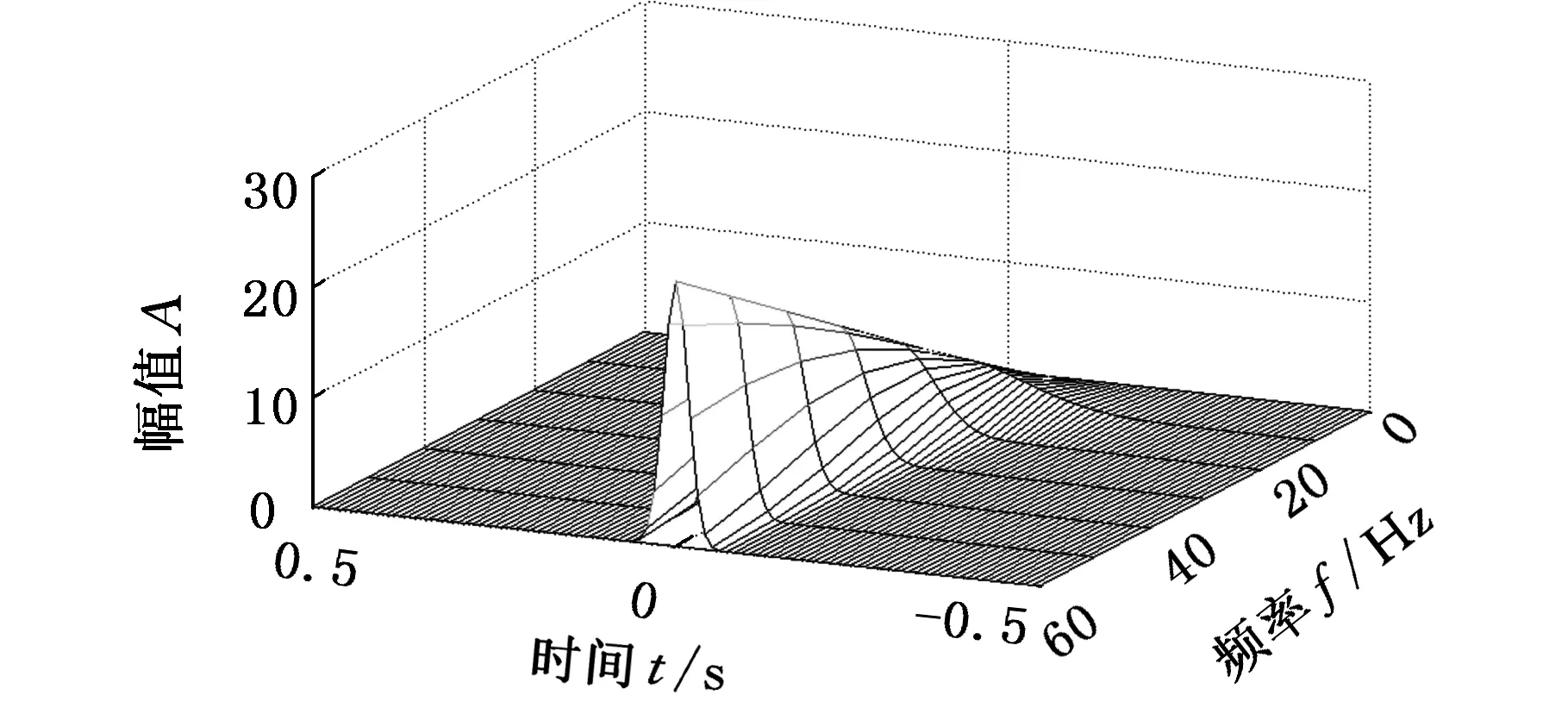
(b)k=1

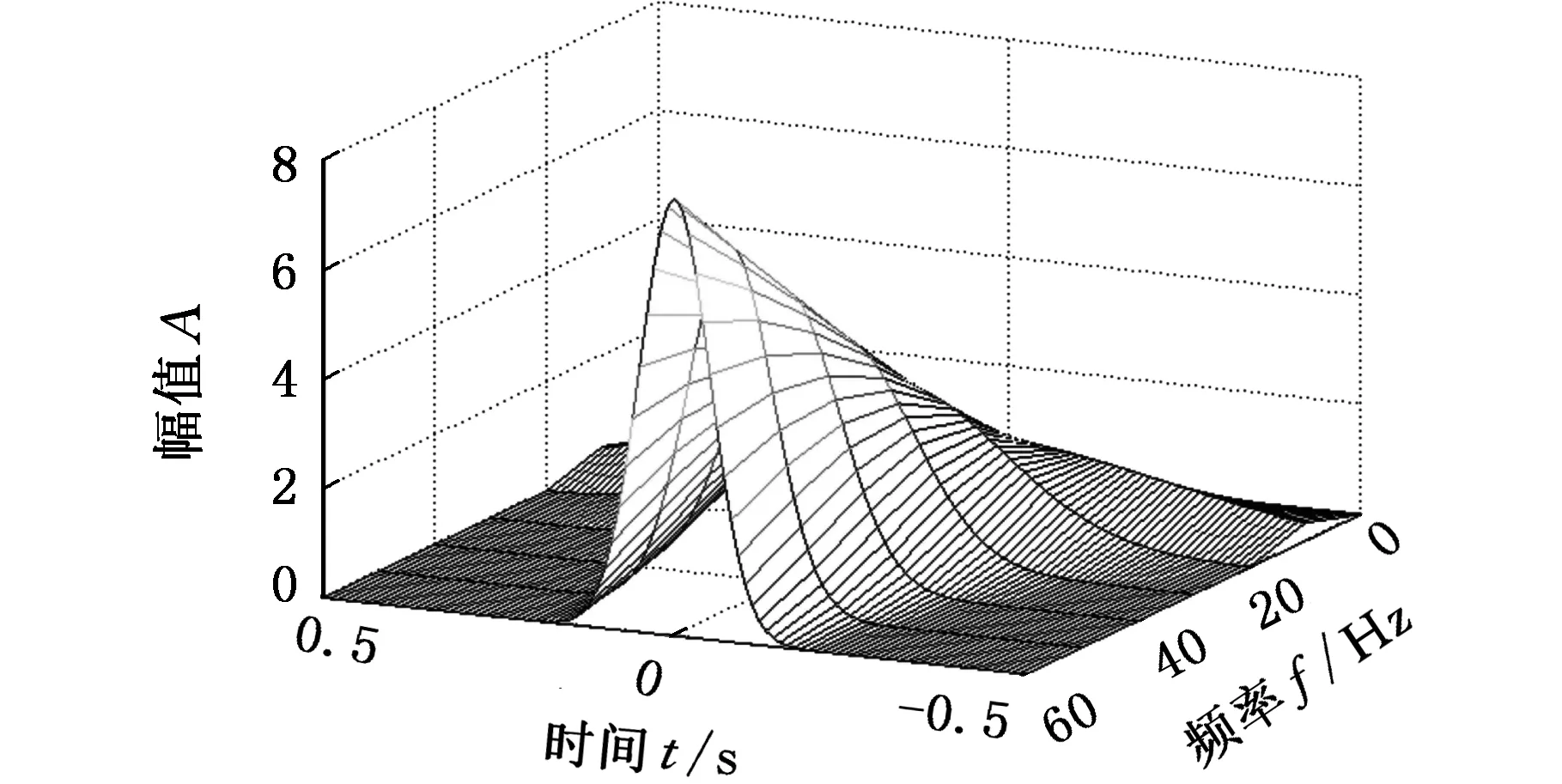
(c)k=3

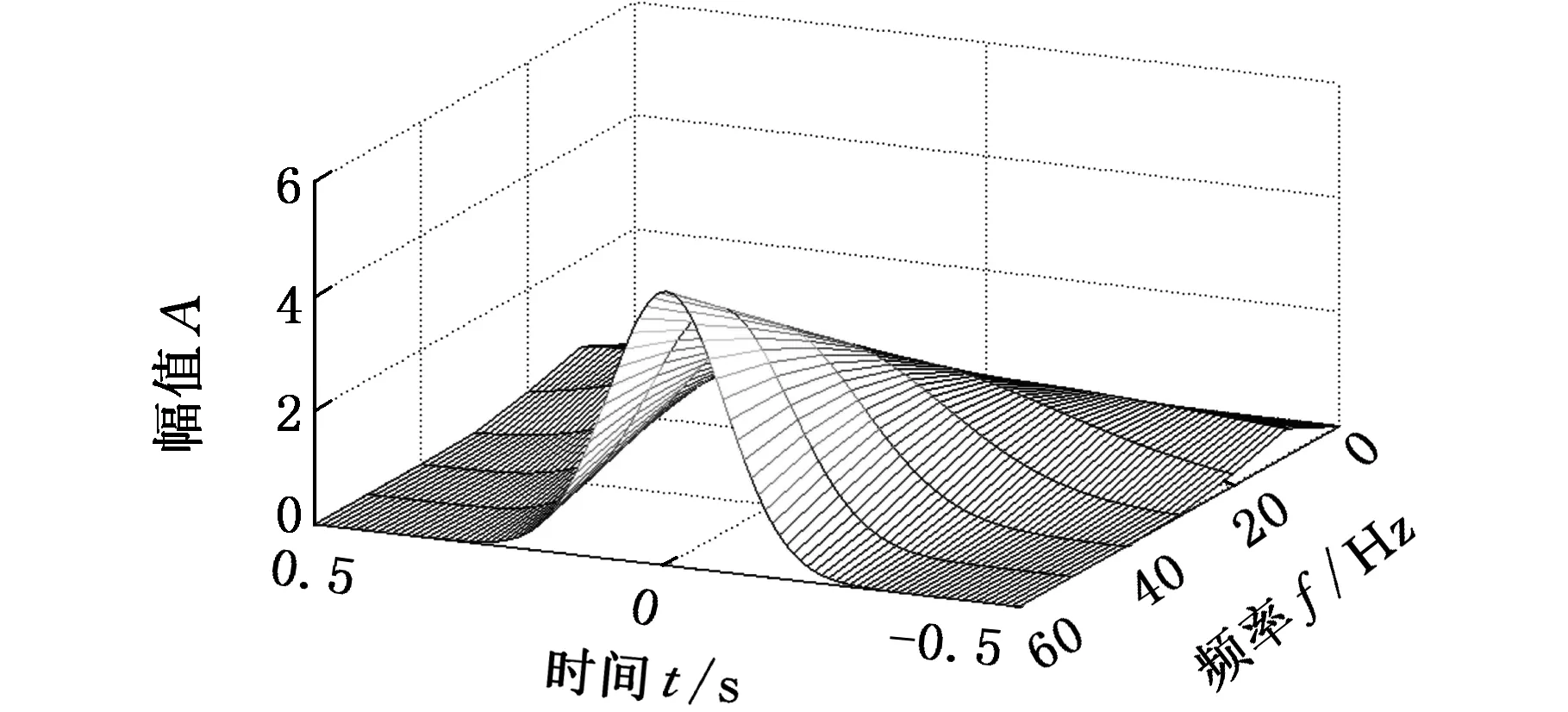
(d)k=5图2 不同k值的广义S变换窗函数Fig.2 The window functions of generalized S-transform in different k values

x(t)=x1(t)+x2(t)+x3(t)+x4(t)+x5(t)

(10)

x1(t)=exp(-αt1)sin(2πf1t)t1=mod(t,1/fb)

x2(t)=sin(2πf2t)

x3(t)=0.8sin(2πf3t)

x4(t)=sin(2πf4t)

x5(t)=0.16rand(n,1)n=length(t)

式中，x1(t)为轴承外圈故障信号和系统结构谐振信号的调制；x2(t)、x3(t)、x4(t)为周期性谐波信号成分；x5(t)为噪声信号；α=400，f1=3500Hz，f2=450Hz，f3=150Hz，f4=48Hz；fb为故障特征频率，fb=33Hz;mod()为取余函数；rand()为随机函数；length()为数组长度函数。

合成信号时域波形及其频谱如图3所示。由图3可知，由于仿真信号中包含有噪声，传统的频谱分析无法识别混合信号中的冲击成分，缺乏“定位”功能，仅从时域图中难以看出冲击特征。现对混合信号x(t)分别进行标准S变换(k=1)和广义S变换(k=6)，其频谱如图4所示。

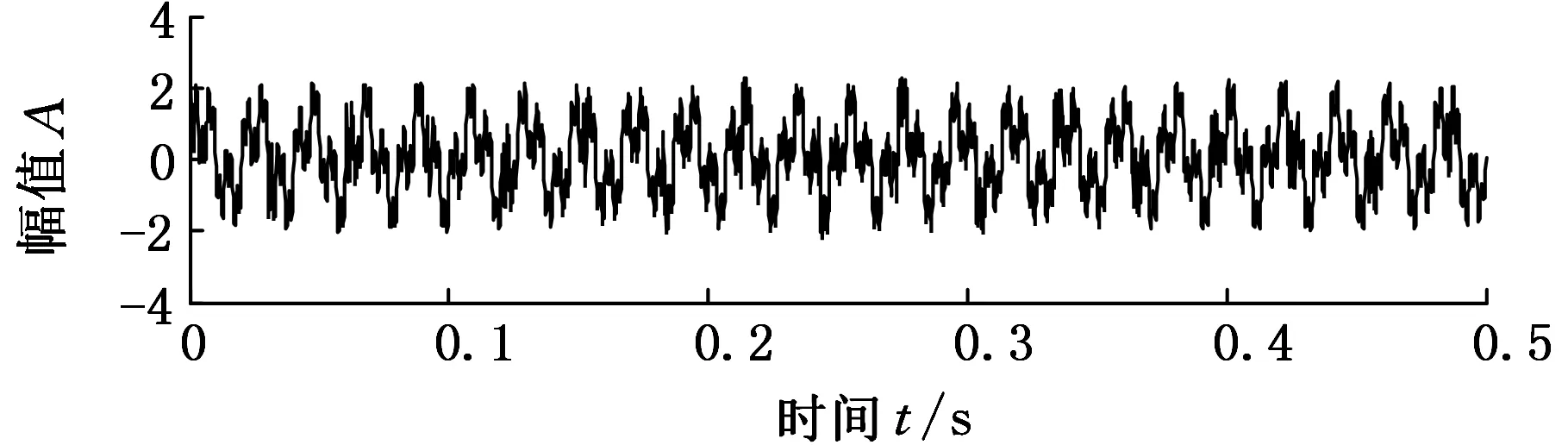
(a)时域波形

(b)频谱图图3 合成信号时域波形及其频谱图Fig.3 Time domain waveformand spectrum of synthetic signal

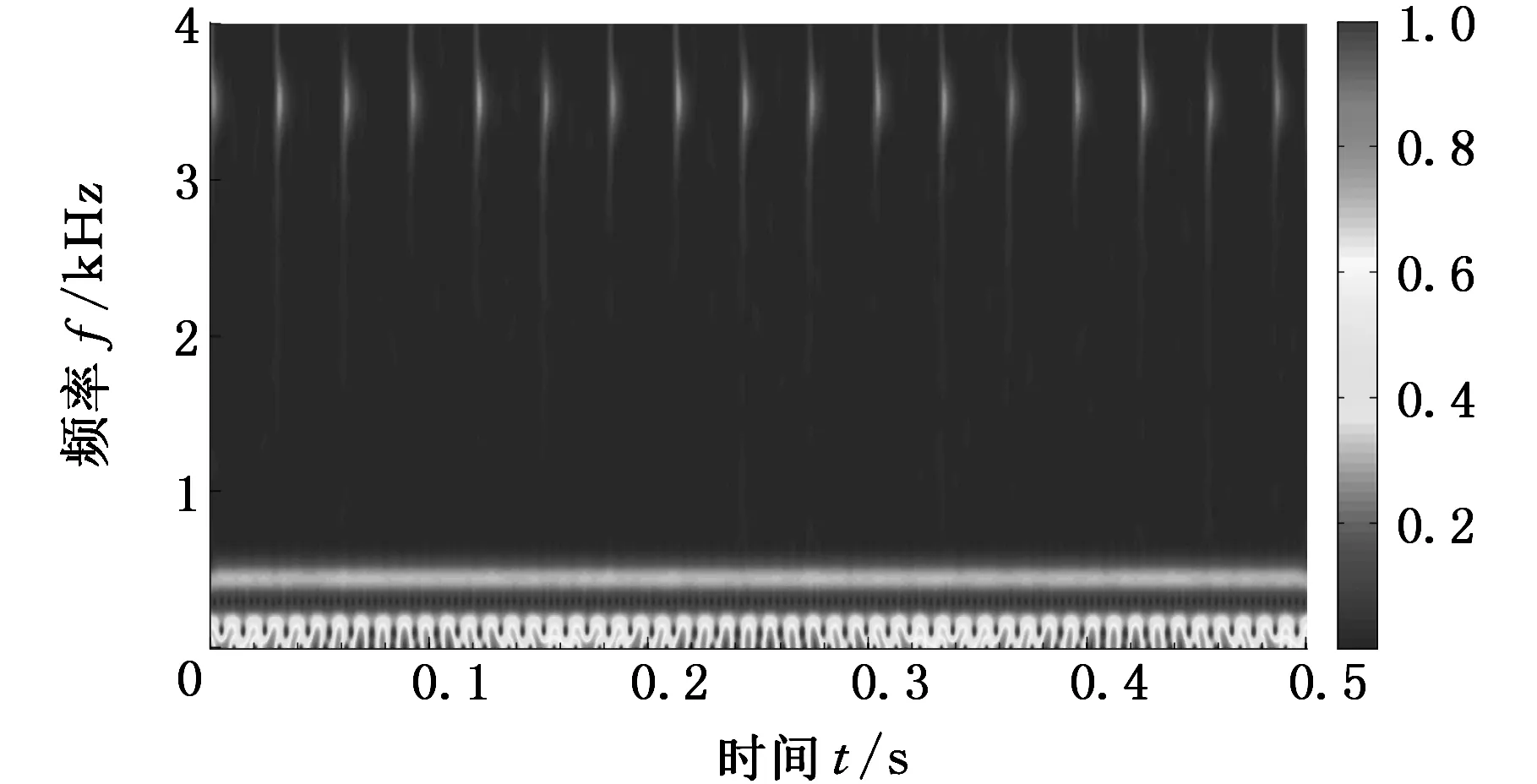
(a)合成信号的标准S变换

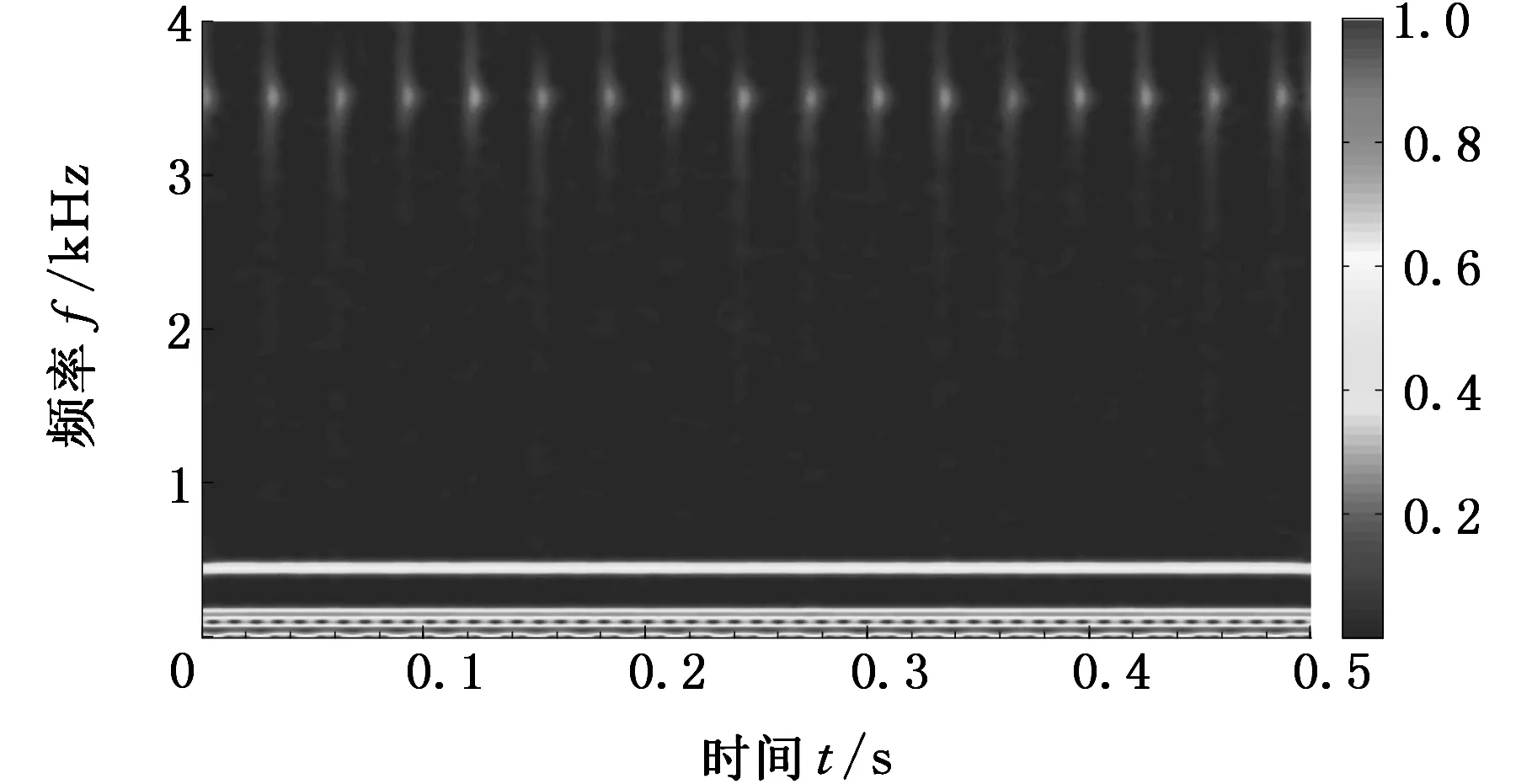
(b)合成信号的广义S变换图4 标准S变换和广义S变换时频谱图Fig.4 Spectrum of S transform and generalized S-transform

在频率轴约3500Hz处，图4a和图4b均出现明显的周期性冲击特征，从对应的时频谱矩阵中找出频率为3500Hz处的信号周期，其周期ΔX约为0.034s，对应频率为33Hz，与仿真实验的故障特征频率(fb=33Hz)相吻合，仿真结果验证了广义S变换时频谱对于非平稳冲击特征提取与分析的有效性。虽然广义S变换和标准S变换均成功地从混合信号中提取出了周期性的冲击特征，但标准S变换的频谱图在各个冲击点处分布不清，时频聚集性不如广义S变换，且广义S变换的时频分辨率明显高于标准S变换的时频分辨率。

时频谱图中各频率成分对应的归一化能量均值大小可以衡量广义S变换结果的优劣，式(10)中x1(t)～x4(t)4种不同频率成分信号的能量均值与k值之间的对应关系如图5所示。由图5可知，周期性谐波信号成分x2(t)、x3(t)、x4(t)广义S变换的能量均值随着k的增大而变大，表明k的取值越大，周期性谐波信号成分的广义S变换时频分辨率越高，能量聚集性越好；在k∈[4,7]时，冲击特征信号x1(t)广义S变换的能量均值不再随着k的变化而变化，且其能量均值达到最大，表明广义S变换时频分辨率达到最佳，能量聚集性最好，此时冲击特征在时频谱图上也最明显。因此选择k∈[4,7]时，广义S变换时频分辨率达到最佳，能量聚集性最好。

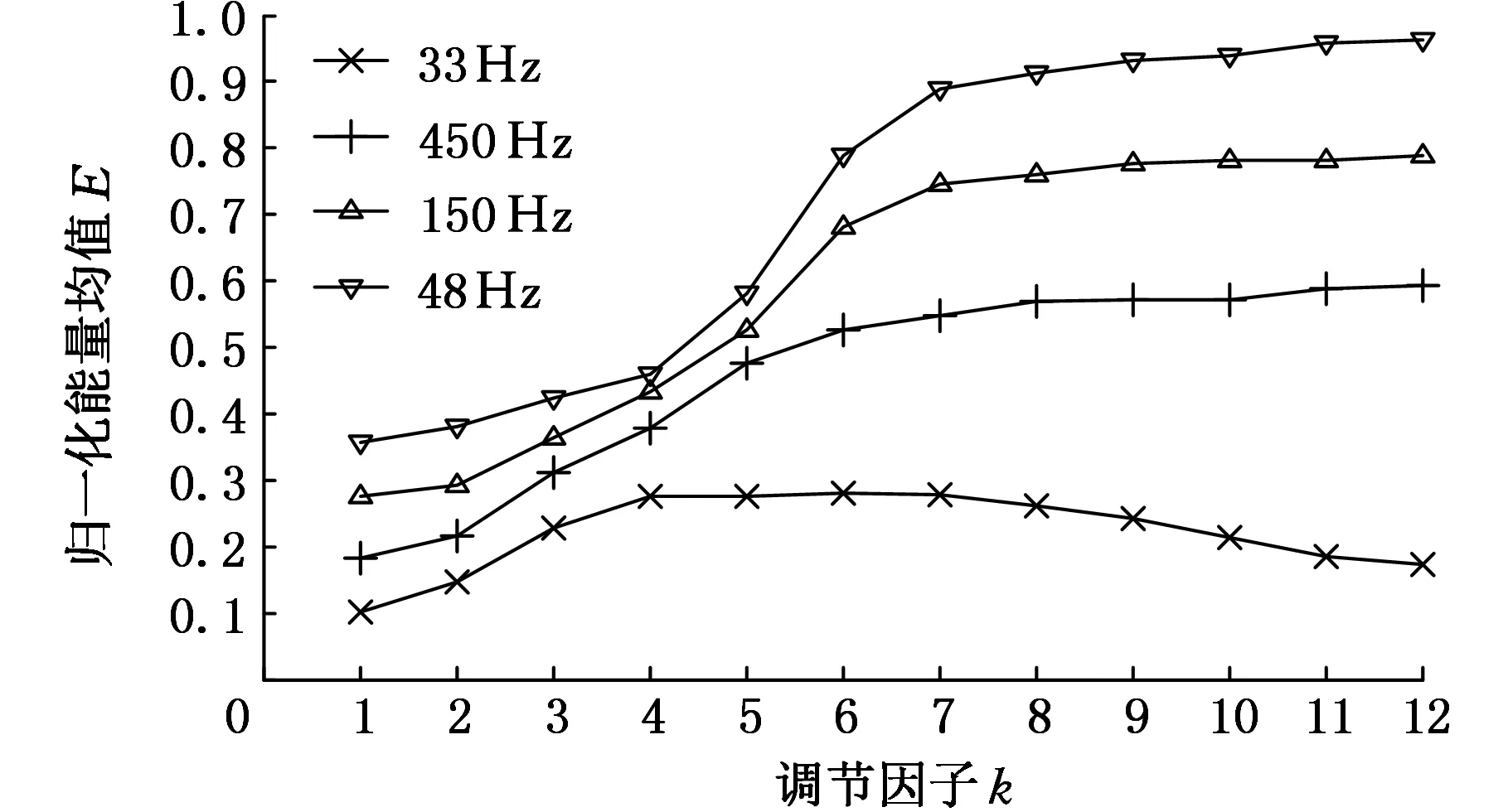
图5 k值与能量均值对应关系Fig.5 Correspondence between k value and energy mean value

4 滚动轴承故障信号实验研究

4.1 滚动轴承冲击特征提取

利用美国凯斯西储大学电气工程实验室的相关轴承数据对所提方法进行验证[11]。轴承故障模拟试验台如图6所示。试验台主要包括1500 W的电动机、扭矩变频编码器、功率计、加速度传感器、控制电子装置 (图中未予以显示)。

图6 轴承振动分析试验台和采集装置Fig.6 Bearing vibration analysis test stand and experimental instrument

电机主轴由被测轴承支撑，而轴承通过电火花加工技术分别植入损伤直径为0.1778 mm、0.3556 mm、0.5334 mm和0.7122 mm 4种不同程度的单点损伤故障。实验中加速度传感器通过磁性底座固定在电机壳体的驱动端和风扇端12点钟方向位置。

本文以6205-2RS型轴承外圈损伤程度为0.7122 mm故障类型作为对象进行分析。实验时轴承转速为1730 r/min，采样频率为12 kHz，轴承故障信号的波形及其广义S变换时频谱如图7所示，由于该信号中包含有较强的背景信号和噪声，仅从波形图中很难看出其中的冲击特征。在图7b的整个时间轴上，频率轴约700 Hz处出现明显的周期性冲击特征，从对应频谱分析的数据库中找出频率为700 Hz处的信号周期，约为0.0080 s，对应频率为124 Hz，与文献[7]结果一致，验证了广义S变换时频谱对于冲击特征提取与分析的有效性。

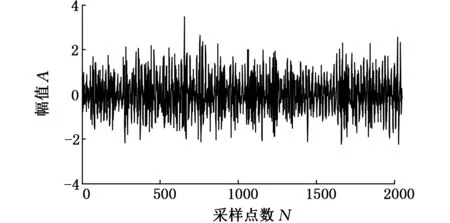
(a)信号波形图

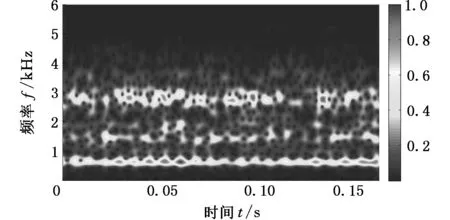
(b)广义S变换时频谱图图7 故障信号的波形图及广义S变换时频谱图Fig.7 Waveform of fault signals and time-frequency spectrum of generalized S-transform

4.2 滚动轴承故障诊断

为了研究不同程度的轴承故障在广义S变换时频谱图上的能量分布，选取相同实验条件下的不同故障程度的滚动轴承实验数据进行广义S变换处理，实验分组和实验条件如表1、表2所示。

表1 实验分组
Tab.1 The group of experiment

组别转速(r/min)电机负载(W)故障直径(mm)a17302237.1(3HP)0.5334b17302237.1(3HP)0.7112

表2 实验条件
Tab.2 The condition of experiment

实验轴承型号故障类型采样频率(kHz)采样数据点数驱动电机功率(kW)6205-2RS轴承内圈故障1220482.2

两组轴承故障振动信号的广义S变换时频谱如图8所示，可以发现图8a和图8b实验数据的广义S变换频谱图在时间轴上的能量分布相近，且均在频率轴上约700 Hz处出现周期性冲击特征，这证明了两者的故障频率是相同的，但图8b的能量明显高于图8a的能量，从图8b对应的时频谱矩阵中找出频率为700 Hz处的归一化能量值，其平均值为0.689，明显高于图8a对应的平均值0.213。

(a)故障直径为0.5334 mm

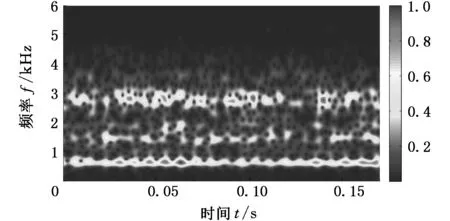
(b)故障直径为0.7112 mm图8 轴承故障振动信号的S变换时频谱图Fig.8 Time-frequency spectrum of bearing vibration signal in S-transform

为了更深入地研究不同程度的轴承故障在广义S变换时频谱图上的能量分布，选取相同实验条件下的3种不同故障程度的滚动轴承实验数据进行广义S变换，相应的归一化能量数值表见表3,损失直径与能量的关系如图9所示。

从表3可知，在相同实验条件下，损伤直径和故障所对应的能量值成正比关系，随着损伤直径的增大，能量值也相应地增大，在广义S变换时频谱图上的能量也越集中，即滚动轴承故障程度越严重。

表3 实验能量表
Tab.3 Energy table of experiment

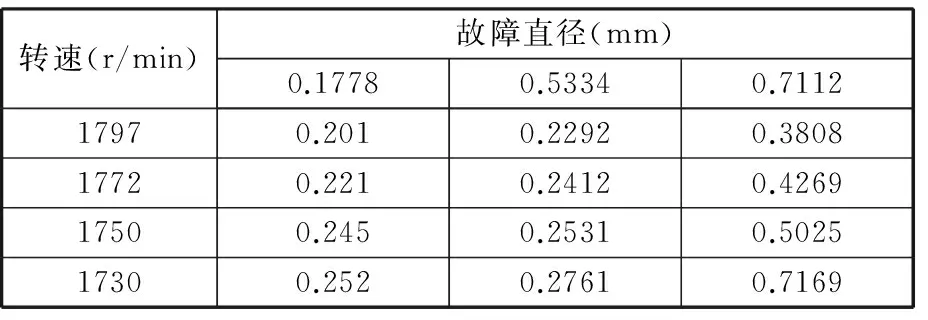
转速(r/min)故障直径(mm)0.17780.53340.711217970.2010.22920.380817720.2210.24120.426917500.2450.25310.502517300.2520.27610.7169

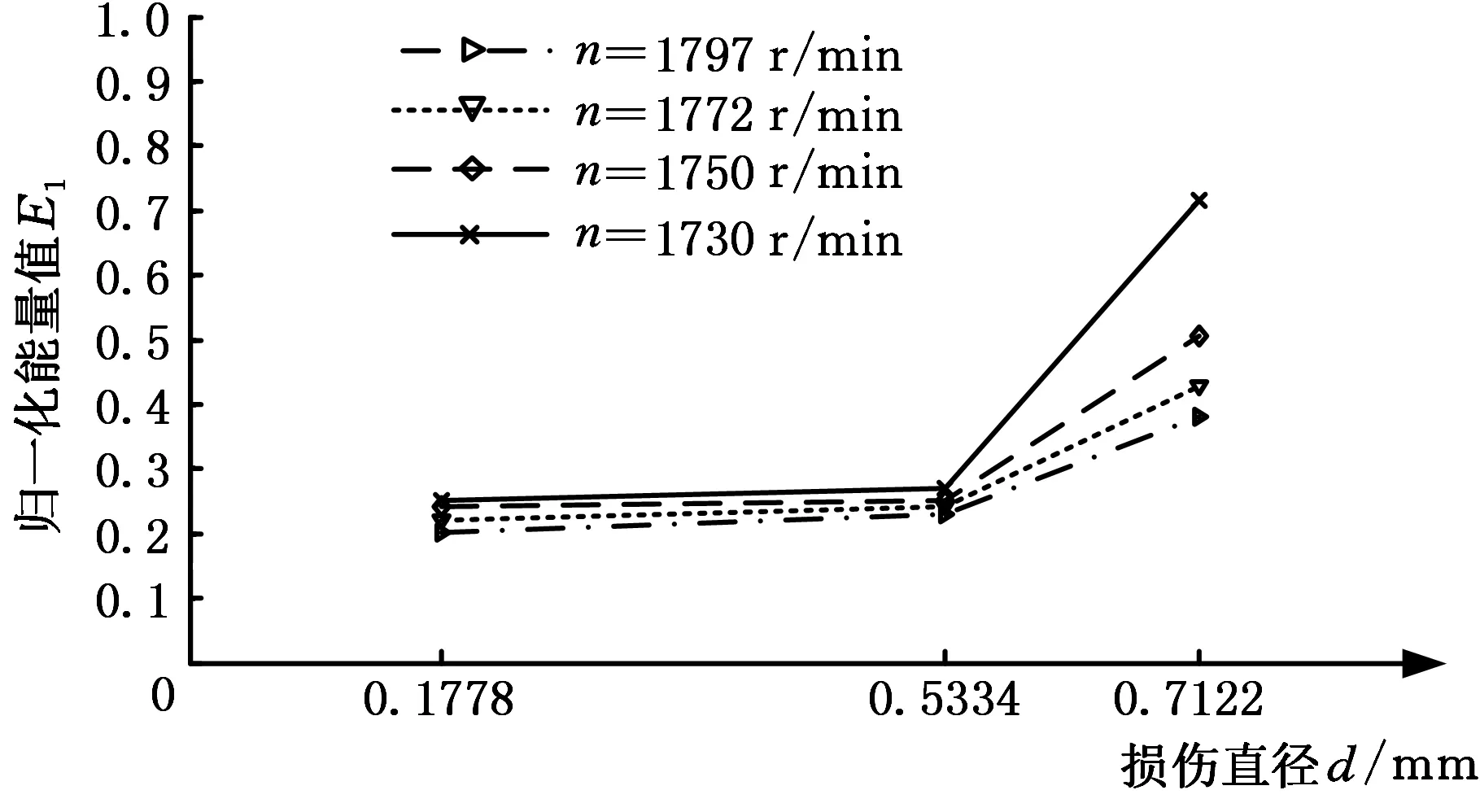
图9 损伤直径与能量关系图Fig.9 Relation between damage diameter and energy

5 结论

(1)讨论了k值对时窗函数宽度和幅值的影响。

(2)提出了一种基于广义S变换的齿轮箱滚动轴承故障诊断方法。仿真和实验结果表明该方法能有效地提取分析轴承故障的特征频率，具有更高灵活性和时频分辨率。

(3)对相同实验条件下不同故障程度的滚动轴承实验数据进行广义S变换处理，验证了在一定范围内，损伤直径和故障所对应的能量值成正比关系。

[1] 钟秉林，黄仁.机械故障诊断学[M].北京：机械工业出版社，2006. ZHONG Binglin，HUANG Ren. Introduction to Machine Fault Diagnosis[M]. Beijing：Mechanical Industry Press，2006.

[2] MALLAT S. A Theory for Multiresolution Signal Decomposition[J].The Wavelet Representation. IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11(7)：674-693.

[3] STOCKWELL R G，MANSINHA L, LOWE R P. Localization of the Complex Spectrum：The S Transform[J].IEEE Transactions on Signal Processing，1996，17(6)：998-1001.

[4] PINNEGAR C R，MANSINHA L. The S-transform with Windows of Arbitrary and Varying Shape[J].Geophysics，2003，68(1)：318-385.

[5] 樊剑，吕越，张辉.基于S变换的地震波时频分析及人工调整[J].振动工程学报，2008，21(4)：381-386. FAN Jian，LYU Yue，ZHANG Hui. Time-frequency Analysis and Artificial Simulation of Earthquake Ground Motions via S-transform[J].Journal of Vibration Engineering，2008，21(4)：381-386.

[6] DASH P K，PANIGRAHI B K. Power Quality Analysis Using S-transform[J].IEEE Transactions on Power Delivery，2003，18(2)：406-411.

[7] 郭远晶，魏燕定，周晓军,等.S变换用于滚动轴承故障信号冲击特征提取[J].振动、测试与诊断，2014，34(5)：818-822. GUO Yuanjing，WEI Yanding，ZHOU Xiaojun，et al. Research on Wireless Measurement System for Film Pressure of Water-lubricated Bearing [J].Journal of Vibration, Measurement & Diagnosis，2014，34(5)：818-822.

[8] 朱明，李志农，何旭平.基于广义S变换的滚动轴承故障诊断方法研究[J].机床与液压，2015，43(1)：181-184. ZHU Ming，LI Zhinong，HE Xuping. Fault Diagnosis Method of Rolling Bearing Based on Generalized S-transformation[J].Machine Tool & Hydraulics，2015，43(1)：181-184.

[9] YANG Wenxian，CHRISTIAN L，RICHARD C. S-transform and Its Contribution to Wind Turbine Condition[J].Renewable Energy，2014，62：137-146.

[10] ROOPA S, NARASIMHAN S V. S-transform Based on Analytic Discrete Cosine Transform for Time-frequency Analysis[J].Signal Processing，2014，105：207-215.

[11] Case Western Reserve University Bearing Data Center[EB/OL]. USA，Tex：Case Western Reserve University,2012[2016-03-01].http://csegroup.case.edu/bearingdatacenter/home.

(编辑 袁兴玲)

Fault Diagnosis Method of Gearbox Bearings Based on Generalized S-transform

CHEN Huanguo YI Yongyu CHEN Wenhua CHEN Pei SHEN Jianyang

Zhejiang Province’s Key Laboratory of Reliability Technology for Mechanical and Electrical Product, Hangzhou, 310018

The signals of gear box bearing faults usually were nonstationary and nonlinear. It might be more difficult to identify and extract in the strong background signals and noises. Based on the unique features and the time-frequency concentration of the generalized S-transform, a rolling bearing fault diagnosis method was proposed based on generalized S-transform. Window function in the generalized S-transform was discussed, and the influences of different parameters in adjusting the width of window function were analyzed, and the different energy distributions of bearing faults were discussed in time-frequency spectrum by generalized S-transform. Finally, the proposed method was validated by simulation analyses and the experiments of rolling bearings. The results show that the proposed method may accurately reveal the rolling bearing fault features frequency, and provides an effective method for gear box bearing fault diagnosis.

gear box; generalized S-transform;fault diagnosis; rolling bearing

2016-03-02

国家自然科学基金资助项目(51475432)；浙江省自然科学基金资助项目(LZ13E050003)；浙江省国际科技合作专项计划资助项目(2013C24005)

TH132.4；TH133.3

10.3969/j.issn.1004-132X.2017.01.009

陈换过，女，1977年生。浙江理工大学机械与自动控制学院副教授。主要研究方向为结构健康监控、结构动力学及信号处理方法。发表论文40余篇。E-mail:chen8025@126.com。易永余，男，1992年生。浙江理工大学机械与自动控制学院硕士研究生。陈文华(通信作者)，男，1963年生。浙江理工大学机械与自动控制学院教授。陈 培,男，1989年生。浙江理工大学机械与自动控制学院硕士研究生。沈建洋，男，1992年生。浙江理工大学机械与自动控制学院硕士研究生。