不确定轮式移动机器人统一自适应神经网络H∞控制

叶锦华 吴海彬

福州大学机械工程及自动化学院，福州，350116

不确定轮式移动机器人统一自适应神经网络H∞控制

叶锦华 吴海彬

福州大学机械工程及自动化学院，福州，350116

提出了一种基于自适应神经网络控制和H∞控制的轮式移动机器人光滑全局跟踪和镇定统一的控制器。首先采用横截函数方法，扩展系统控制输入，建立与原系统等价的、输入输出完全解耦的无奇异全驱动系统，再对新系统设计自适应神经网络H∞控制器。自适应神经网络控制可有效补偿系统的复杂不确定项。H∞控制器可同时对系统扰动和神经网络逼近误差进行预定水平抑制，进一步提高控制器的适应性，优化系统的控制性能。仿真结果验证了算法的有效性。

轮式移动机器人；轨迹跟踪与镇定统一控制；自适应神经网络；H∞控制；横截函数

0 引言

非完整轮式移动机器人(wheeled mobile robots，WMR)是一类典型的多输入、多输出非完整系统，其控制器设计的困难一方面在于系统不满足Brockett的必要条件[1]，不存在光滑时不变静态状态反馈镇定控制律，另一方面在于系统存在控制输入欠驱动。解决这两个困难的单一控制方法已取得较为丰富的研究成果[2-4]，但是只有少数学者进行了WMR统一控制器的研究[5-13]。统一控制器可以避免实际应用中采用单一控制器组合时的切换控制，有利于提高系统的动态性能和稳定性。然而采用时变控制器[5]易产生控制输入高频震荡，采用基于极坐标方法[6]和动态反馈控制方法[7]设计的控制器存在潜在的奇异，而镇定控制往往需要额外的限制条件来解决奇异问题。鉴于此，文献[8]采用横截函数方法实现WMR的无奇异“实际线性化”，即通过扩展控制输入解决系统的欠驱动问题。但文献[8]仅讨论了理想系统，而实际的WMR系统总存在模型的不确定性，不可避免地受到外界干扰的影响。文献[5]基于Lyapunov直接法和反演设计技术，在系统参数不确定的情况下，设计了WMR全局时变输出反馈自适应统一控制器，但该控制器适用于不确定参数为固定或慢时变的状况。文献[9]基于WMR的扩展Heisenberg系统形式，采用滑模控制技术设计了一类统一控制器，但该控制器易产生抖振现象。文献[10]结合微分平坦和高维动态扩展方法设计了WMR的统一控制器，该控制器仅对WMR转动轴上的常值干扰具有鲁棒性，鲁棒性能有限。

为了弥补上述方法的不足，笔者基于横截函数方法设计了WMR的统一控制器，提出一种结合自适应RBF神经网络(adaptive RBF neural network, ARBFNN)控制和H∞优化控制的方法。通过H∞控制对外界未知扰动和ARBFNN的逼近误差进行预定水平鲁棒抑制，进一步提高了控制器的控制性能。

1 问题的描述

一般带漂移项的非完整机械系统可表示为

(1)

式中，广义坐标向量q属于一个n维流形G；Xi为系统的光滑控制向量场；ui为控制输入；P*(q，t)为系统的未知不确定漂移项；τd为未知外部扰动。

当Xi为左不变向量场时，称系统(式(1))为左不变系统。

本文研究符合unicycle类型的(2，0)型WMR[14]，即m=2，n=3，定义q=[x y θ]T，u=[u1u2]T，u1、u2分别为WMR的前进速度和绕质心轴的转动速度，则有

X1=[cosθsinθ0]T

X2=[0 0 1]T

向量场X1、X2满足李代数的秩条件[8]，因此， unicycle型WMR是局部能控的。轨迹跟踪控制时，为避免跟踪误差系统出现结构上的奇异，参考轨迹需要满足随时间变化的“持续激励”条件[15]。镇定点为与时间无关的固定常数，从而导致跟踪控制器无法直接用于镇定控制，这给跟踪和镇定统一控制器的设计带来了障碍，文中通过横截函数方法来解决这样的问题。

横截函数方法首先构造一个可微横截函数：

f(α):Tn-m→μ

(2)

式中，“·”表示群运算符。

注意到q∈SE(2)，且易验证unicycle型WMR为左不变系统，即∀q1,q2∈G:dLq1(q2)X(q2)=X(q1q2)，其中，Lq1表示q1的群左平移操作，dLq1(q2)表示Lq1对q2的微分，则对式(2)求导，并将式(1)代入可得

(3)

D=P*(q，t)+τde=[0 0 0]T

其中， Rq表示q的群右平移操作；ur=[ur1ur2]T为轨迹参考速度。令z=[z1z2z3]T，进一步引入横截函数，并构建新的误差方程：

(4)

对(4)式求导可得

(5)

(6)

(7)

则式(5)可化为

(8)

式(8)是一个包含原系统等价不确定项的线性系统，可见，即使D为不匹配不确定项，在新系统下也实现了解耦匹配，这给控制器的设计带来极大的方便。

横截函数f(α)的存在与否是横截函数方法的一个关键，可以通过式(6)的横截条件来判定一个函数是否构成横截函数。同一系统横截函数的构造并不唯一，文中取横截函数为

易验证该函数可以满足横截条件。对f(α)求导后可得

于是有

其中，ε1、ε2为设计参数，ε1>0，ε2>0。显然ε1、ε2取值越小，f(α)越接近于平衡点e。系统稳态误差越小，控制器的增益越大，这导致系统的控制量加大，这容易引起控制器饱和，因此应根据实际需要对ε1、ε2进行合理取值。

文中的研究问题是基于误差系统(式(8))，设计WMR的统一控制器，实现WMR的全局渐进稳定跟踪和镇定控制，并消除系统未知不确定和扰动的影响。

2 控制器设计与分析

本文将ARBFNN控制同H∞优化控制结合起来，使控制器能适用于同时包含未知参数和非参数不确定性的复杂系统，提高了神经网络控制的收敛速度。ARBFNN控制器用于补偿不确定漂移项P；H∞控制器不仅保证系统控制性能，还能保证对扰动τd和ARBFNN控制器补偿误差ε的预定水平抑制。

因为式(8)是一个线性系统，所以可对z中每个变量分别进行控制器设计，定义

则下式成立：

(9)

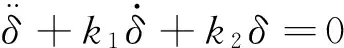
(10)

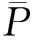
(11)

(12)

式中，ψ为网络输入，ψ=[iZ1iZ2]；W为权重，W=[w1w2…wl]T∈Rl；l为连接节点数，l>0；径向基ζ(ψ)=[c1c2…cl]T；μl=[μl1μl2]T为隐含层神经元感应区的中心点;ηl为高斯函数的基宽；ω为RBFNN的逼近误差。

当W为最优值时，ω的值最小。定义估计值为

(13)

对于H∞控制，是在让系统稳定的所有控制器中，选择一个使得抑制信号到系统输出的传递函数的H∞范数最小的控制器，保证整个系统满足H∞控制性能。对线性系统(式(9))而言，H∞控制器的设计可归结为求解Riccati代数方程的过程，设计H∞鲁棒控制项v为

v=-δTPB/γ

(14)

式中，γ为正的常数；B=[0 1]T；P为正定矩阵。

通过如下Riccati代数方程来求解P：

PA+ATP+Q+(1/μ2-2/γ)PBBTP=0

(15)

其中，Q为给定的正定矩阵。μ(μ>0)为预定抑制水平值，为了保证获得半正定解P，应满足2μ2>γ，将式(10)、式(11)代入式(9)可得

(16)

设计自适应律为

(17)

式中，λ为正常数。

(18)

T∈[0，∞) Ψ∈L2[0，T]

证明：选择候选正定Lyapunov函数为

(19)

对式(19)求导，并将式(14)、式(16)代入可得

(20)

再将式(15)、(17)代入式(20)有

δTPBΨ)/2=

-[δTQδ+(BTPδ/μ-μΨ)T(BTPδ/μ-μΨ)-

μ2Ψ2]/2≤(μ2Ψ2-δTQδ)/2≤

(21)

(22)

因为V(T)≥0，则有

(23)

而

(24)

将式(24)代入式(23)可得式(18)，定理证明完毕。

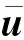
3 仿真实验

通过MATLAB环境下的仿真实验来验证文中控制器的有效性和控制效果。首先进行控制器的控制参数配置，对Ui取k=[1 1]T，显然可以使得矩阵A的特征根都在左半开平面，取Q为2×2的单位矩阵，γ=0.01，预定抑制水平μ=0.16，求解式(15)所示的Riccati代数方程可得到

横截函数的设计参数取ε1=0.08，ε2=0.2，α(0)=0。假设WMR系统在8～10s内受到轮子的侧滑扰动，定义打滑模型为

其中，打滑幅度ϖ(t)=0.6，假设系统的不确定项为

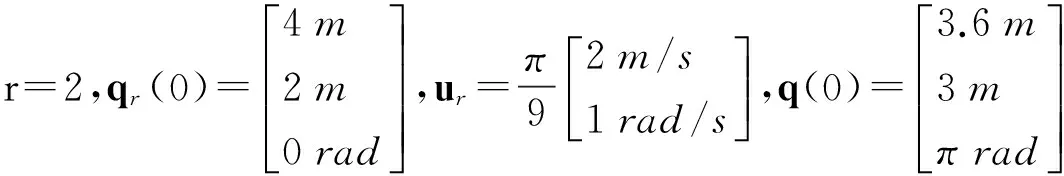
首先对WMR使用文献[8]提出的比例控制器。由图1可知，由于受到不确定性的不利影响，普通控制器无法进行有效补偿，轨迹跟踪过程存在较大的控制误差，改变控制器增益时，控制效果仍不能得到改善。使用文中所提控制器，在关闭ARBFNN即仅使用H∞控制器时，轨迹跟踪结果如图2所示。通过H∞控制的鲁棒抑制，跟踪效果得到了一定的改善，但由于系统不确定性较为复杂，故仍存在较为明显的跟踪误差。

图1 文献[8]控制器的轨迹跟踪结果Fig.1 Track locus of controller in reference[8]

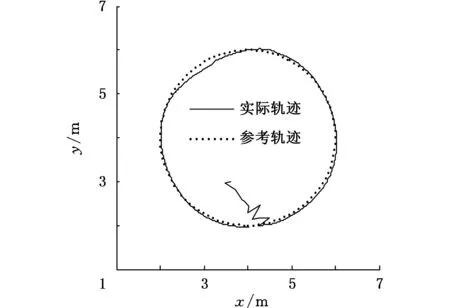
图2 关闭ARBFNN时文中控制器的轨迹跟踪结果Fig.2 Track locus of the proposed controller when ARBFNN is closed

开启ARBFNN后的轨迹跟踪如图3所示。从图3和表1可以看出，系统扰动和不确定性项得到了有效补偿，文中控制器取得良好的控制效果，保证WMR精确地跟踪参考轨迹。

(a)文中控制器轨迹跟踪结果

(b)轨迹跟踪误差

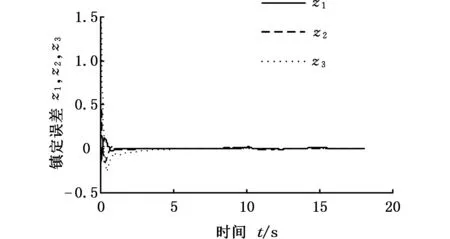
(c)新误差系统状态变化情况图3 文中控制的轨迹跟踪仿真结果Fig.3 Simulation results of track locus of the proposed controller

文献[8]控制器H∞控制器文中控制器Δx(mm)19.95.30.16Δy(mm)25.67.80.38Δθ(rad)0.12890.08780.0013

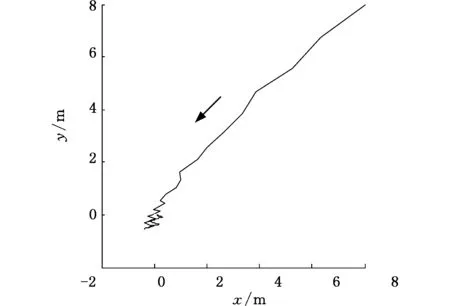
(a)点镇定过程

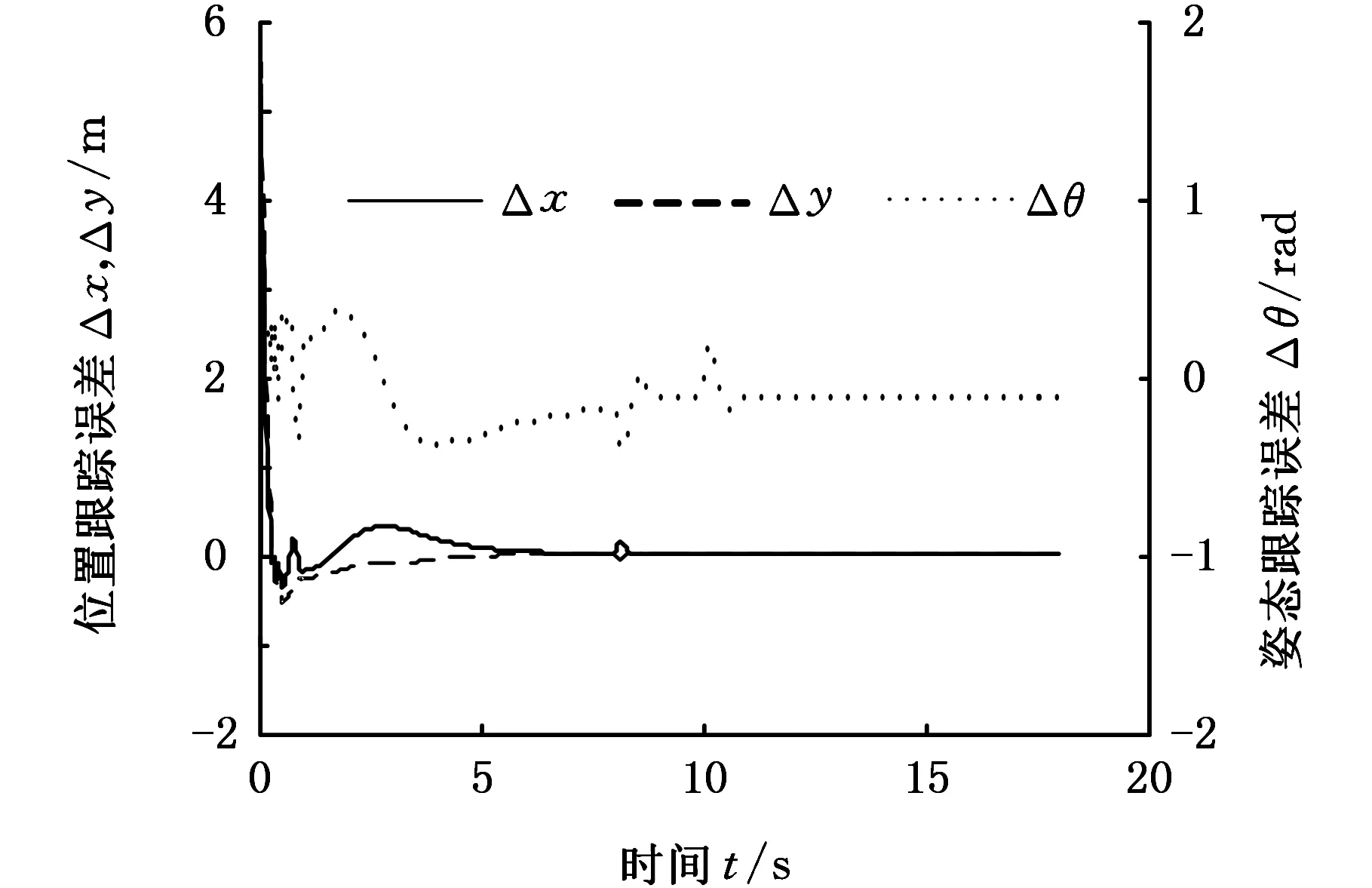
(b)镇定误差变化情况

(c)新误差系统状态变化情况图4 点镇定仿真结果Fig.4 Simulation results of point stabilization

使用统一控制器对WMR进行点镇定控制，取q(0)=[8m8m0rad]T，仿真结果如图4所示。从图4a可以看出，系统实现镇定后，尽管受到轮子打滑扰动的干扰，WMR仍很快又恢复到平衡值，消除了系统不确定和外部扰动的影响。由图4b、图4c可知，系统稳定时的镇定误差为有界值(|Δx|≤1.9mm，|Δy|≤3.4mm，|Δθ|≤0.042rad)，这是横截函数方法实际镇定的结果。值得一提的是，镇定误差有界值可以通过调整设计参数ε1和ε2来改变，以满足不同系统实际应用需求。

4 结语

研究了包含不确定和外部扰动的WMR轨迹跟踪和镇定统一控制器设计问题，针对WMR变量耦合和欠驱动问题，利用原系统对群运算的左不变性，采用横截函数方法进行解耦和控制输入扩展。横截函数方法将镇定控制的渐进镇定于原点放宽为实际有界镇定，尽管仅获得有界的控制精度，却取消了对参考轨迹“持续激励”条件的限制，让光滑时不变反馈的统一控制律的设计成为可能，并保证控制器的全局性。在此基础上，针对系统存在的不确定性和外部扰动，通过结合ARBFNN控制和H∞控制，在对系统复杂不确定性进行有效补偿的同时，对系统扰动和ARBFNN

逼近误差进行预定水平抑制，提高了控制器对高度不确定系统的适应性，保证了控制器优化的控制性能。对圆弧轨迹跟踪控制和原点镇定控制的仿真结果表明，该统一控制器可消除系统不确定性和外部扰动的影响，提高轨迹跟踪和镇定效果。

[1] BROCKETT R W. Asymptotic Stability and Feedback Stabilization[M]. Boston：Birkhauser，1983.

[2] 叶锦华，李迪，叶峰. 输入受限非完整移动机器人的自适应模糊控制[J].中国机械工程，2014，25(8)：1010-1016. YE Jinhua，LI Di，YE Feng. Adaptive Fuzzy Control of Nonholonomic Mobile Robots with Bounded Inputs[J]. China Mechanical Engineering，2014，25(8)：1010-1016

[3] Al-Araji A S，ABBOD M F，Al-RAWESHIDY H S. Applying Posture Identifier in Designing an Adaptive Nonlinear Predictive Controller for Nonholonomic Mobile Robot[J]. Neurocomputing, 2013, 99: 543-554.

[4] AROGETI S A, BERMAN N. Path Following of Autonomous Vehicles in the Presence of Sliding Effects[J]. IEEE Transactions on Vehicular Technology，2012，61(4)：1481-1491.

[5] HUANG J S, WEN C Y, JIANG Z P. Adaptive Stabilization and Tracking Control of a Nonholonomic Mobile Robot with Input Saturation and Disturbance[J]. System & Control Letters, 2013, 62: 234-241.

[6] SUM S L, CUI P Y. Path Tracking and a Practical Point Stabilization of Mobile Robot[J]. Robotics and Computer-Integrated Manufacturing, 2004, 20: 29-34.

[7] MA M M, HONG C, LIU X J. Tracking and Stabilization Control of WMR by Dynamic Feedback Linearization[C]//Chinese Control and Decision Conference. Beijing，2011: 3430-3435.

[8] MORIN P，SAMSON C. Control of Nonholonomic Mobile Robots Based on the Transverse Function Approach[J]. IEEE Transactions on Robotics, 2009, 25(5): 1058-1073.

[9] DEFOORT M, DJEMAI M. Finite-time Controller Design for Nonholonomic Mobile Robot Using the Heisenberg Form[C]//IEEE International Confer-ence on Control Applications. Lille，France，2010: 1269-1274.

[10] BUCCIERI D, PERRITAZ D, MULLHAUPT, et al. Velocity-scheduling Control for a Unicycle Mobile Robot-theory and Experiments[J]. IEEE Transactions on Robotics, 2009, 25(2): 451-458.

[11] MICHALEK M, KOZLOWSKI K. Unified Approach to Trajectory Tracking and Set-point Control for a Front-axle Driven Car-like Mobile Robot[C]//IEEE American Control Conference. Poznan，Polan，2011: 1112-1117.

[12] MA M M, LI S, LIU X J. Tracking Control and Stabilization of Wheeled Mobile Robots by Non-linear Model Predictive Control[C]//Proceeding of the 31st Chinese Control Conference. Hefei，China, 2012: 4056- 4061.

[13] ZHU X C, DONG G H, CAI Z X，et al. Robust Simultaneous Tracking and Stabilization of Wheeled Mobile Robots not Satisfying Nonholonomic Constr-aint [J]. J. Cent. South Univ. Techno., 2007, 14(4): 537-545.

[14] YU W, CHUY O Y, COLLINS E G, et al. Analysis and Experimental Verification for Dynamic Modeling of a Skid-steered Wheeled Vehicle[J]. IEEE Transactions on Robotics, 2010, 26(2): 340-353.[15] LEE T C, LEE C H, TENG C C. Tracking Control of Unicycle-modeled Mobile Robots Using a Saturation Feedback Controller[J]. IEEE Transactions on Cont-rol Systems Technology,2001,9(2):305-318.

(编辑 张 洋)

Unified Adaptive Neural NetworkH∞Control of Uncertain Wheeled Mobile Robots

YE Jinhua WU Haibin

School of Mechanical Engineering and Automation, Fuzhou University,Fuzhou，350116

A smooth global unified controller of trajectory tracking and stabilization was proposed for nonholomomic wheeled mobile robots based on adaptive neural network control andH∞control. Firstly, the system control inputs were expanded by transverse function method, a nonsingular full drive system which was equivalent to original system was established with decoupled input-output. Then an adaptive neural networkH∞controller was designed for the new system, such that the complex system uncertainty was compensated effectively by the adaptive neural network. Disturbances and approximation errors were attenuated with a prescribed disturbance lever by theH∞control. Adaptability of the controller were further improved, and the control performance was optimized. The effectiveness of the algorithm were verified by simulation results.

wheeled mobile robot; unified control of trajectory tracking and stabilization; adaptive neural network;H∞control; transverse function

2015-12-29

2016-09-30

国家自然科学基金资助项目(51175084)；福建省自然科学基金资助项目(2015J05121)；福州大学科研启动基金资助项目(510078)；福州大学科技发展基金资助项目(650053)

TP24

10.3969/j.issn.1004-132X.2017.02.005

叶锦华，男，1982年生。福州大学机械工程及自动化学院讲师。主要研究方向为机器人技术。发表论文10余篇。E-mail:yejinhua@fzu.edu.cn。吴海彬，男，1973年生。福州大学学院机械工程及自动化学院教授、博士研究生导师。