长江下游径流潮汐河口段河相关系研究

张玮，徐鹏

（河海大学港口海岸与近海工程学院，江苏 南京 210098）

长江下游径流潮汐河口段河相关系研究

张玮，徐鹏

（河海大学港口海岸与近海工程学院，江苏 南京 210098）

长江下游径流潮汐河口段受径流与潮汐共同作用，影响河床形态动力因素复杂。参照以往有关研究成果，推导出适用于径流潮汐河口段的河相关系；以长江下游澄通河段为例，利用大范围潮流数学模型，计算沿程各断面的过水面积与径流和潮流流量，验证河相关系的合理性。研究结果表明：对于径流潮汐河口段，水流包括径流部分与潮流部分，相应地，过水断面也可分为径流塑造部分与潮流塑造部分；对于径流潮汐河口段，即使有径流存在，在潮量与潮流塑造的过水断面之间也存在良好的相关关系；根据推导过程来看，所得河相关系式应该普遍适用于整个河口段，但分析表明，其可能更适合径流潮流河段，也就是潮流界以下河段。

径流潮汐河口段；河相关系；数值模拟

0 引言

径流潮汐河口段的河床形态是流域来水来沙、海洋潮汐动力等相互作用的结果，其间存在着一定关系，通常称为河相关系。河相关系的研究旨在寻求河床地貌形态与动力因子的定量关系，是认识河道特性以及整治航道[1]的主要技术手段之一，一直为人们所关注。

长江下游江阴至徐六泾的澄通河段，既受上游径流来水来沙影响，又受下游海洋动力作用，属于典型的径流潮汐河口段，河相关系复杂。有关河相关系，国内外曾先后开展过大量研究，特别是有关潮量或流量与过水面积之间的关系，成果颇丰。1930年，O′Brien[2]在调查美国太平洋砂质侵蚀海岸潮汐通道时，提出潮量和断面面积（相对于平均海平面）之间的表达式；1953年，Leopold和Maddock[3]提出在准平衡状态的天然河流中，给定的河宽、平均水深、平均流速与流量之间存在着简单类似的函数关系，也就是河相关系；1964年，窦国仁将河床最小活动性原理应用到潮汐河流，提出平均水深、平均河宽和平均断面面积与落潮平均流量、落潮平均含沙量河相关系式[4]；1988年，高抒对中国东海11个海湾通道资料进行统计后亦得到断面面积与纳潮量的关系[5]；2010年，韩曾萃等在海湾通道断面面积与纳潮量关系的基础上，进一步将径流、落潮历时、落潮含沙量的河口河相关系应用于海湾，并验证了浙江省的杭州湾、象山港、三门湾、乐清湾等区域25个断面的河相关系[6]；2014年，赵子辉利用最小活动性原理结合新的水流挟沙力公式，重构窦国仁河相关系公式，建立了一个新的适用于潮汐河口的河相关系公式[7]；2015年，张玮和曹昊建立了灌河河口落潮流量与过水断面面积之间的关系，并对不同河道形态的理想宽深比及其在航道整治中的应用进行了讨论[8]。上述研究中，主要针对径流或者潮流单独作用的情况，即使有些研究也涉及径流潮汐河口段，但是并没有深入探讨径流或者潮流的各自贡献。

本文拟利用O'Brien提出的潮汐通道纳潮量与断面面积河相关系，同时参考窦国仁有关河口动力的处理方法，推导出适用于径流潮汐河口段的河相关系，可以分别考虑径流与潮流的贡献；以澄通河段为对象，建立长江下游潮流数学模型，计算求得所需各量，由此对于所推导的河相关系进行验证。

1 径流潮汐河口段河相关系的建立

参照O'Brien方法，潮量和断面面积之间的关系表达式[5]为：

式中：P为平均大潮潮差下的潮量；A1为平均海平面下河口断面面积；k为常数（河口断面特性决定）；S为含沙量。

参照窦国仁方法，如果潮汐河口在一个潮汐周期T内的冲淤数量能够相互抵偿，在此时期内上游来水量以及下游海口涨入的水量必然等于同一时期内落潮期间河床断面所能排泄的水量。令表示时间内的上游来水量，同一时期内涨潮流期间下游涨入的水量为纳潮量。为了落潮期间能够排泄上述水量，河床必须具有如下水力几何形态：

式中：B为平均潮水位时的水面宽；H为相应的平均水深；v为平均落潮流速；T落为单个潮汐周期内的总落潮历时。

用Q表示落潮流（包括上游径流）的平均流量，用Q0表示落潮期间上游平均径流量，则有：

将式（1）代入式（3），并经转换可得：

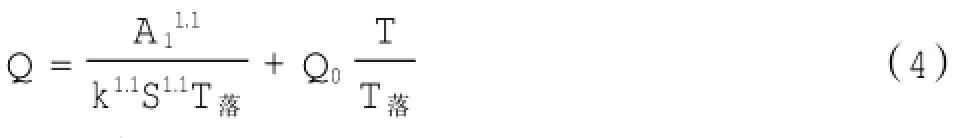
其中：

式中：A为平均过水断面面积（总的过水面积，包括径流作用和潮流作用所产生的过水面积）；A0为径流产生的平均过水断面面积；A1为潮流产生的平均过水断面面积。

对于径流潮汐河口段上游的冲积性河流，仅受径流作用，有如下河相关系式[9]：

式中：B′为平均河宽；H′为相应平均水深；k1、k2、m、n为常数。

由于

将式（6）、式（7）代入式（8）可得：

式中：k3、e为常数。

将式（9）代入式（5）得：

将式（10）代入式（4）得：

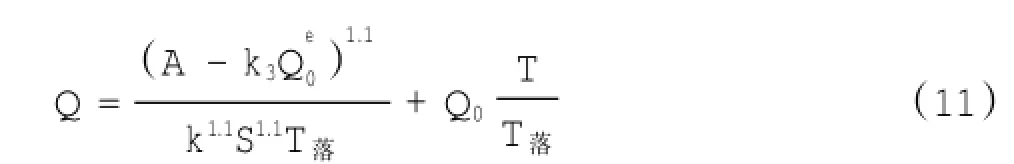
或者

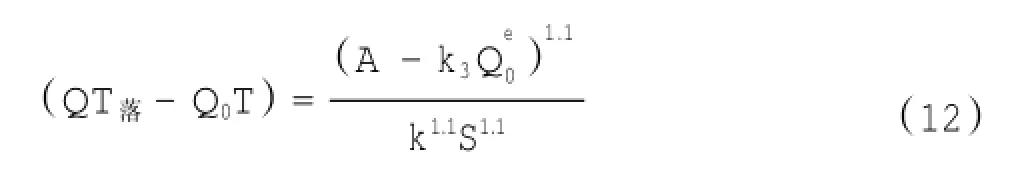
以下将以澄通河段为例，通过建立长江下游潮流数学模型，计算澄通河段沿程各断面的过水面积与流量，对式（12）进行验证。

2 长江下游潮流数学模型的建立

模型范围上起安徽大通，下至南支杨林、北支青龙港。采用一维和二维耦合技术建立数学模型，安徽大通至江阴芦埠港河段采用一维模型，以下河段采用二维模型。

2.1 基本控制方程

在一维潮流数学模型中，采用Saint-Venant方程组作为控制方程，其连续方程和运动方程可以表示为：

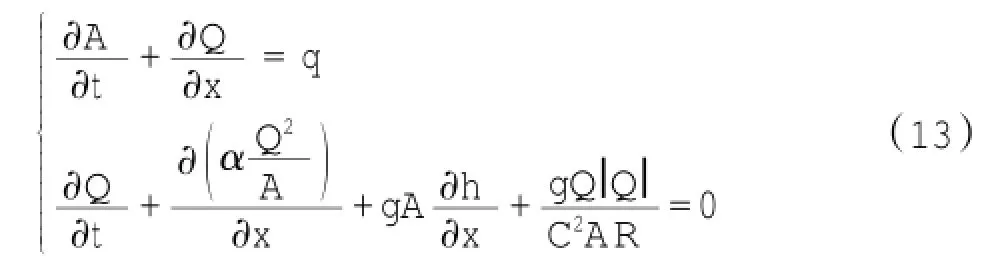
式中：x和t分别为距离和时间的坐标；A为过水断面面积；Q为流量；h为水位；q为旁侧入流的流量；C为谢才系数；R为水力半径；α为动量校正系数；g为重力加速度。

在二维潮流数学模型中，连续方程为：

运动方程为：

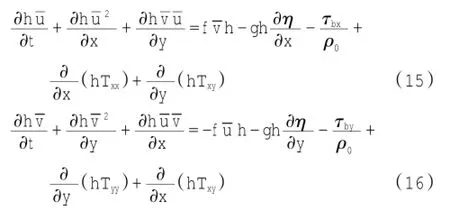
其中：x、y为笛卡尔坐标；t为时间变量；η为水位；d为总水深，且有h=d+η，d为静水深；为x、 y方向深度平均速度；τbx、τby为x、y方向底部应力；ρ0为水的密度；f为科氏力系数，且f=2Ω sin Ψ；g为当地重力加速度；Txx、Tyy、Txy为水平黏滞应力项。

2.2 模型概况

一维模型从大通站至江阴芦埠港全长412.5 km，共设置188个断面；二维模型从江阴芦埠港至模型下游边界，全长约135.8 km，模型共有75 172个网格，最小网格尺度为50 m，以保证计算精度。

2.3 模型验证

为使所建立的潮流数学模型能较好地模拟实际水流的运动情况，需对模型进行率定和验证，确定其中的计算参数。以往曾分别利用2004—2008年多次实测水文资料对该模型进行率定，本次研究中又选用长江澄通河段2010年7月进行的水文测验数据对于模型进一步验证。经过验证，计算结果与实测值吻合较好。

3 径流潮汐河口段河相关系研究

3.1 计算工况的选取

长江口属于非正规半日潮，在一个潮汐周期中，上游大通站的径流量基本保持不变，因此，可以将其设为定值。选取5种不同工况，分别为2010年7月16日大潮，2010年8月13日大潮，2010年4月30号大潮，2010年4月15日大潮，2010年1月16日大潮，对应上游大通径流量分别为61 200 m3/s、54 000 m3/s、43 000 m3/s、29 200 m3/s、12 600 m3/s。

3.2 计算断面的选取

以澄通河段为例开展研究。利用2010年长江下游水下实测地形图，将澄通河段分为15个断面，断面位置见图1。

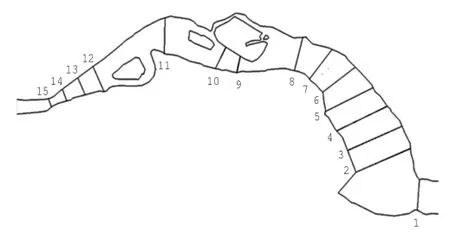
图1 澄通河段断面位置图Fig.1 Sectional positions of the Cheng-Tong reach

在分析过程中，将根据潮流数学模型的计算结果，经过整理得到所需各量，例如式（12）中落潮流量与落潮历时的乘积：

式中：t为某断面落潮期间任意一个整点时刻；t0为该断面落潮起始时刻；t1为该断面落潮结束时刻；Qt为该断面时刻的流量。

在计算过水断面积时，将各个断面的河宽20等分，由程序输出这21个坐标点在平均潮位下的水深，运用以下公式：

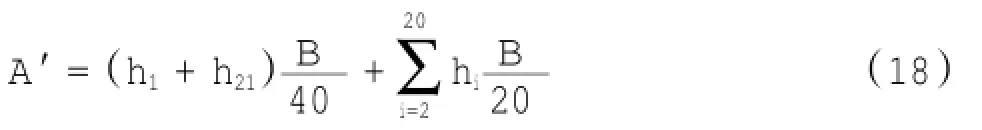
式中：A′为平均过水断面面积（断面选取在澄通河段即为A，断面选取在上游径流河段即为A0）；h1、h21为该断面两端坐标点在平均潮位下的水深；hi为该断面上第i个坐标点在平均潮位下的水深；B为该断面河宽。

3.3 径流河段河相关系

选取澄通河段上游大通段河段（仅受径流作用）进行式（9）的拟合，模拟该河段2010年日平均流量与日平均水位以下的过水断面面积的关系，详见图2，得到以下公式：

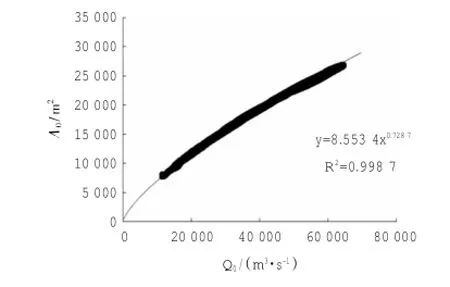
图2 仅受径流作用下长江下游河段断面过水断面面积与流量关系Fig.2 The relationship between the cross-sectional area and the discharge of the lower reaches of the Yangtze River only by the runoff

3.4 径流潮汐河口段河相关系

建立澄通河段5种计算工况下的平均过水面积与之间的关系。将（A+A0）1.1与作为散点，点绘于平面（x，y）坐标系，并进行线性回归分析，结果详见图3。由图可以得到公式：

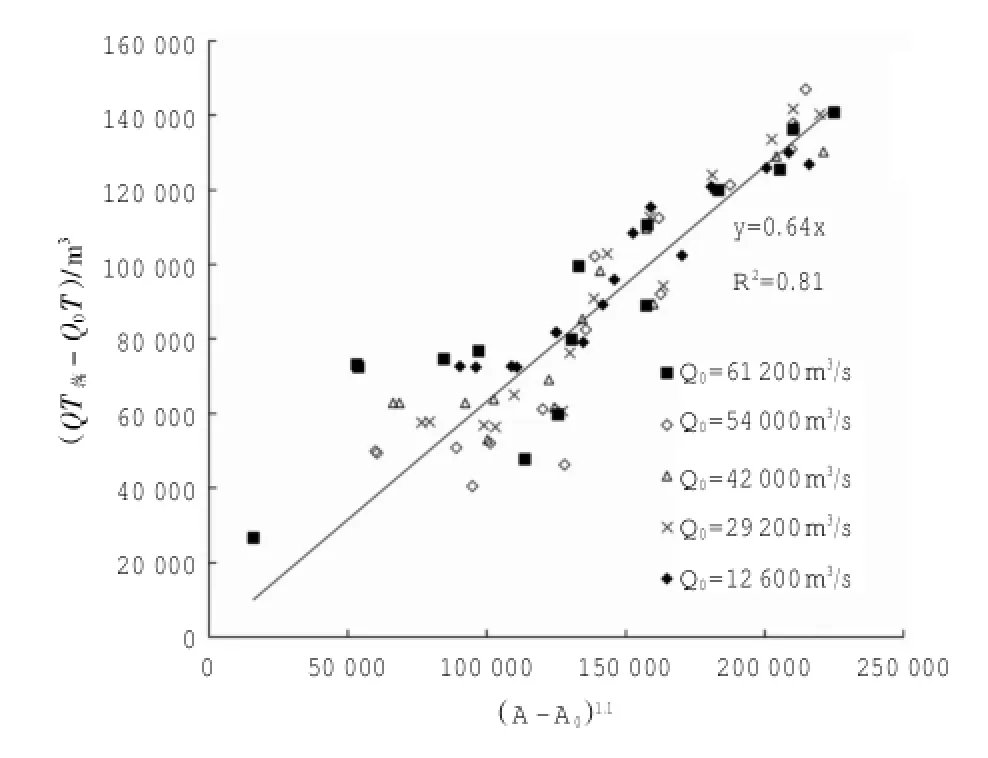
图3 澄通河段河相关系图（1～15号）Fig.3 The hydraulic geometry of the Cheng-Tong reach (No.1～15)

由此可见，对于澄通河段这样的径流潮汐河口段，潮流动力塑造的部分断面面积与落潮量之间存在良好的相关关系，相关系数平方高达0.81，也就是相关系数为0.9。

3.5 河相关系的讨论

在式（20）中，等式左侧第一项为一个潮汐过程中径流与潮流综合下泄总量，第二项为径流下泄总量，两者之差反映的就是河段的纳潮量；等式右侧括号中，第一项为过水断面总面积，第二项是径流单独作用所对应的过水断面，两者之差反映的是潮流所塑造的河床断面。由此可见，原本适用于纯潮汐河段的O'Brien河相关系式，在经过适当变换后，也可应用于径流潮汐河口段，同样表达的是潮量与河床断面之间的相互关系。

根据公式的推导过程来看，式（20）应该普遍适用于径流潮汐河口段。但如进一步分析则可以发现，这个公式可能更适合潮流径流河段，也就是潮流界以下河段。例如，对于洪季流量61 200 m3/s，根据计算结果，此种工况下的潮流界大约位于10号断面附近，这也就意味着11～15号断面已没有涨潮流出现，不再属于径流潮流河段。此时，如果去掉这几个断面的数据，则式（20）的相关系数会进一步提高，相关系数的平方值R2由0.81提高到0.88，相应地，相关系数则由0.90提高到0.94。有关这个现象的深层次原因，还需在今后的工作中进一步深入探讨。

4 结语

1）对于纯潮汐河口段，过水断面仅与潮汐作用也就是潮量有关；而对于径流潮汐河口段，水流包括径流部分与潮流部分，相应地，过水断面也可分为径流塑造部分与潮流塑造部分。

2）根据O'Brien提出的过水断面与潮量之间的相关关系，同时参照窦国仁方法，推导出适用于径流潮汐河口段的河相关系，结果表明：即使有径流存在，在纳潮量与潮流塑造的过水断面之间也存在良好的相关关系。

3）以澄通河段为例，借助于潮流数学模型，计算了过水断面与径流和潮流流量等，验证了所推导河相关系的正确性，相关系数高达0.9以上。

4）根据公式的推导过程，所得河相关系应该普遍适用于径流潮汐河口段。但分析表明，所得公式可能更适合径流潮流河段，也就是潮流界以下河段，此时，相关系数甚至可以达到0.94。

[1]姜继红，冯宏琳，张玮，等.天然河流航道整治定级的理论计算方法[J].中国港湾建设，2006（2）：20-22. JIANG Ji-hong,FENG Hong-lin,ZHANG Wei,et al.Theoretical calculation on defining rating of waterways of natural rivers after waterwayregulation[J].China Harbour Engineering,2006(2):20-22.

[2]O'BREIN M P.Estuary tidal prisms related to entrance areas[J]. Civil Engineering,1931,1(8):738-739.

[3]LEOPOLD L B,MADDOCK R T.The hydraulic geometry of stream channels and some physiographic implications[J].Usgs Professional Paper,1953,252:56.

[4]窦国仁.平原冲积河流及潮汐河口的河床形态[J].水利学报，1964（2）：1-13. DOU Guo-ren.Riverbed morphology of alluvial plains rivers and tidal estuaries[J].Journal of Hydraulic Engineering,1964(2):1-13.

[5]高抒.东海沿岸潮汐河道的P-A关系[J].海洋科学，1988（1）：15-19. GAO Shu.P-A relationships of tidal incets along the East China Sea coast[J].Marine Sciences,1988(1):15-19.

[6]韩曾萃，朱宝土，唐子文.河口、海湾断面与潮量关系的一致性及其应用[J].浙江水利科技.2010（5）：1-5. HAN Zeng-cui,ZHU Bao-tu,TANG Zi-wen.Coherent relationship between cross-section area and tidal prism of estuary and bay [J].Zhejiang Hydrotechnics.2010(5):1-5.

[7]赵子辉.长江感潮河段河相关系及其应用研究[D].南京：南京师范大学，2014. ZHAO Zi-hui.Research and application of hydraulic geometry to reach of the Yangtze River[D].Nanjing:Nanjing Normal University, 2014.

[8]张玮，曹昊.灌河河相关系及航道整治设想[J].水道港口，2014（2）：40-45. ZHANG Wei,CAO Hao.Morphological relationships and suggestion on waterway regulation in Guanhe River[J].Journal of Waterway and Harbor,2014(2):40-45.

[9]赵晓马.顺直冲积性河道河相关系和稳定指标研究[D].重庆：重庆交通大学，2009. ZHAO Xiao-ma.Experimental study on regime relationship and stability index mark of straight alluvial river[D].Chongqing: Chongqing Jiaotong University,2009.

Morphological relationships of runoff tidal estuary on the lower reaches of the Yangtze River

ZHANG Wei,XU Peng
（College of Harbor,Coastal and Offshore Engineering,Hohai University,Nanjing,Jiangsu 210098,China）

The runoff tidal estuary of the lower reaches of Yangtze River is affected by the runoff and tide;these dynamics affecting the riverbed sectional morphology are complex.According to the previous research results,we deduced the morphological relationship applicable to the runoff tidal estuary.Taking the Cheng-Tong River on the lower reaches of the Yangtze River as an example,with the help of the established large-scale flow mathematical models,we calculated the cross water area along river of each section and the discharge of runoff and tidal current to verify the rationality of the morphological relationships.The result shows that:for the runoff tidal estuary,the flow includes the runoff and tidal current,and correspondingly,water cross-section can also be divided into parts of the runoff shaping and tidal current shaping;for the runoff tidal estuary,there is a good correlation between the tidal prism and the cross-section area of the tidal current shaping,even if runoff exists.According to the derivation of the formula,the morphological relationship formula should be generally applicable to the runoff tidal estuary,but in practice this formula may be more suitable for the runoff tidal current estuary,which is below the tidal current boundary.

runoff tidal estuary;morphological relationships;mathematical simulation

U612.23；TV147

A

2095-7874（2017）01-0019-05

10.7640/zggwjs201701004

2016-10-28

交通运输部建设科技项目（2014328J17170）

张玮（1958— ），男，山东青岛市人，教授，博士生导师，主要从事港口航道工程研究。E-mail：zhangweihhu@vip.sina.com