国内外连续管软件研究分析

明瑞卿 贺会群 唐纯静 胡强法

1.中国石油勘探开发研究院；2.中国石油集团钻井工程技术研究院

连续管（Coiled Tubing）是一种由钢带成型、可缠绕运输的无接箍焊接管。近十年来，由于具有使用效率高（移运方便、安装迅速、快速起下），可进行气举、冲砂、清洗等连续循环作业，允许带压作业（压裂、酸化）等诸多优点，连续管技术不仅在常规油气井中应用普遍，而且在非常规油气的勘探开发中也获得了广泛的认可［1-2］。

通过国家科技重大专项“连续管装备与应用技术”（2011ZX05036）、中石油集团公司项目“复杂结构井连续管作业技术应用基础研究”（07A100102）、“连续管钻井技术与装备”（2011B-4304）等项目的支持，以及中国石油集团公司“连续管作业技术推广专项”（2011B-1711）的推动，由中国石油钻井工程技术研究院负责统筹的项目团队开展了连续管技术的研究、应用与推广，取得了以下成果：（1）连续管作业机和连续管钻机的研制（CT38连续管作业机与LZ580-73T连续管钻机）；（2）连续管井下作业工具的研制（连续管钻井定向器和井下减速器）；（3）连续管工艺技术的研究（连续管钻井、井下作业、完井管柱、储层改造与采油开发技术）。目前，国内已经实现了连续管装备与工具的配套，促进了规模化应用。但因诸多原因，对连续管软件技术一直未开展系统的研究，设计与分析软件长期依赖进口，严重制约了连续管技术的进一步发展。针对这个问题，首先对国外先进的连续管作业软件进行系统总结，然后对国内外连续管软件现状进行了综合对比与分析，并给出软件编制所需的相关模型及其适应性与选择依据，最后对国内连续管软件技术的发展提出了具体建议。

1 国内外研究现状

Domestic and foreign research status

国外从20世纪90年代就开始研究连续管软件技术，目前已推出多款商业化的软件产品，例如MEDCO（Modelling Engineering & Development Company）的Fatigue Analysis for Coiled Tubing（FACT）和 Tubing Analysis System（TAS）软件，NOV（National Oilwell Varco）旗下公司CTES开发的Cerberus软件，斯伦贝谢（Schlumberger）公司开发的CoilCADE软件。其中Cerberus软件在全球的应用范围较为广泛，其与设备高度配套，以致安全系数和作业效率较高，且能适应连续管技术规模应用和高端复杂作业、复杂井况作业的需求，代表了国际上连续管软件技术的最高水平。

国外先进的连续管作业软件，覆盖了连续管作业设计、施工分析的各个环节，并在持续发展，主要包括基本分析模块（力学模型、水力学模型和疲劳模型）和典型工艺设计模块（气举、冲砂、速度管柱和钻磨桥塞等）。

1.1 Cerberus软件

Cerberus software

当使用连续管起下钻时，操作者可使用Cerberus预测和分析作业各阶段连续管的受力情况与疲劳。该软件能确定可到达的目标深度和工作的完成情况，并可确保井下管柱和工具系统安全返回地面。其关键特性就是能模拟斜井和水平井的井下情况，并能在极端条件下给出最佳工作方案。该软件的结构及功能如图1所示。

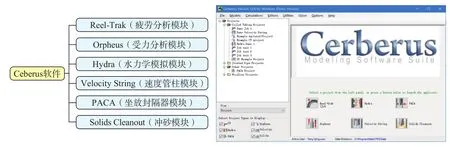
图1 Cerberus软件结构及功能Fig. 1 Structure and function of Cerberus software

1.1.1 Reel-Trak（疲劳分析模块） Reel-Trak模拟软件可以用来预测、追踪和分析连续管的疲劳和径向变形情况。作业前的预测和作业中的实时监测，既可以作为目标管串工作后分析的一部分，也可以用于管串设计，使当前作业时的管串使用率最大化来优化投资回报率。

该模块的总体工作流程主要分为新建工作、启动工作、疲劳追踪和事后分析4个部分。其核心主要是根据塑性理论和Tulsa大学Steven Tipton建立的Achilles 3.0模型（包含了连续管材料、几何参数、内压、弯曲半径和此次弯曲前连续管的状态）来得到连续管特定部分的疲劳损耗。

1.1.2 Orpheus（受力分析模块） 在确定施工的可行性时，必须计算出影响连续管作业的机械力和液压力。Orpheus可计算出这些作用力并提供及时反馈，确保用户能够顺利解决相应问题。其核心是当连续管起下钻时，通过基础TEM计算方法可得出一口井指定深度沿着管串上的受力情况（先从尾管开始计算，再计算出管尾到地面每段管串的受力情况）。

1.1.3 Hydra（水力学模块） Hydra模块可设计和模拟连续管泵送流体的作业工况，并进行相应的水力学计算（流量与压力等）。根据现场实际情况，先设置工具串、井筒、作业流体、初始流体分布等基本参数，其中流体类型包括气体、泡沫和多相流，然后通过Hydra可看到井下、地面、工具等的真实图像、流体特性及瞬时位置。

1.1.4 Velocity String（速度管柱模块） 速度管柱是一根直径较小的管柱，可以解决井筒输送液体速度不足的问题，而液体不及时排出会造成累积并且不利于生产。安装速度管柱可以减少流动面积，增加流动速度，从而使液体从井筒中顺利排出。

通过比较IPR曲线（描述储层的流动特性）和J曲线（描述气体在管柱内的流动特性），速度管柱模块可计算出速度管柱的最佳特性，给出其优化设计，目的是为了找到一个能恢复井筒生产的最优化连续管尺寸和安装深度，以便使摩擦压降最小化，生产能力最大化，且井筒能持续生产足够长的时间来抵消速度管柱的安装成本，使其在预期的应用中效果最大化。

1.1.5 PACA（坐放封隔器模块） 当地面或者井底条件发生变化（地面管柱上提力和下放力的变化、井底温度梯度的变化、管柱或环空中流体的变化、流量变化、管柱或环空中压力的变化），PACA模块可计算出封隔器上的管柱运动情况、管柱作用在封隔器上的力和封隔器作用在套管上的力。

1.1.6 Solids Cleanout（冲砂模块） 在Solids Cleanout模块初始阶段时，用户需要先新建工程或选择已存在的工程，输入必要的基本参数（井筒、沉砂、设备和流体等），然后输入各阶段泵速，并调整作业参数，最后可计算出井筒冲砂时所需的泵速和泵压。

1.1.7 适用性及不足 中石油钻井工程技术研究院、中石油川庆钻探公司、中石油海洋工程有限公司及中海油能源发展有限公司等国内各大石油公司所使用的连续管软件均是NOV所研发的Cerberus软件，目前国内该软件的应用主要集中在受力分析模块、水力学模块及钻磨桥塞模块，经现场应用，模拟结果与实际作业数据接近，精确度较高。

但该软件的引进费用高，升级费高，有用户限制和封锁，只支持自身的采集系统。而且该软件在语言标识、计算单位制、作业习惯及后期培训等方面存在一系列问题，导致工程技术人员使用该软件有一定的困难，故Cerberus软件在国内的应用水平有待提高。

1.2 井下连续管力学分析软件

Downhole coiled tubing mechanics analysis software

2011年西南石油大学的王安义等研发了井下连续管力学行为分析软件［3］。该软件具有如下功能：（1）绘制井眼轨迹。基于井眼轨迹数据库（井斜角、井深、井斜方位角等），软件可绘制出二维井眼轨迹（垂直井眼轨迹、定向井眼轨迹与水平井眼轨迹）和三维井眼轨迹（水平视图与侧视图）。（2）计算循环系统压耗。计算出连续管不同作业条件下各部分循环系统的流体压耗（连续管内部、环形空间、钻头和喷嘴），还可计算出连续管内外压力值。（3）分析应力。该软件可计算出连续管不同作业工况下所受轴向载荷，进行相关应力分析和强度校核。（4）分析注入头所受载荷。软件可计算不同作业条件下连续管起下钻时注入头所受载荷，分析并给出载荷与测量深度的关系。

1.3 连续管钻井水力参数计算软件

Coiled tubing drilling mechanic parameter calculation software

2014年长江大学的管锋等［4］研发了连续管钻井水力参数计算软件。该软件基于Visual Basic语言，结合传统计算模型、油田现场作业条件与试验结果编写而成。根据输入的相关参数，给出连续管钻井施工中推荐的合理排量和最小泵压。其主要特点：（1）界面简单，操作方便，符合油田现场操作人员要求；（2）对现场连续管施工有一定的指导意义；（3）功能单一，只适用于钻井作业，且输出参数较少。

1.4 连续管流体特性参数分析软件

Coiled tubing fluid property parameter analysis software

2015年西南石油大学练章华等［5］开发了连续管流体特性参数分析软件。该软件是以Visual Studio 2013作为开发平台，结合三大模型（幂律流体、牛顿流体和宾汉流体）、油田现场施工所用的流体类型、连续管基础参数和井身结构等编写而成。软件需要输入的参数有连续管技术参数、滚筒尺寸、流体类型和井身结构，而软件的主要输出包括流态、流体流速、环空压耗与任意位置的压力值，井眼轨迹的2D/3D显示，排量-泵压曲线和压力变化曲线等。其主要特点如下：（1）界面简单，操作方便，功能齐全；（2）适用于水平井和垂直井；（3）适用于连续管多种作业模式。

2 对比分析

Comparative analysis

NOV CTES、Schlumberger和 Baker Hughes等国外石油公司的连续管软件技术研发已近几十年，经历了开发、测试、修改完善、现场应用和再修改完善的循环过程，形成了成熟的连续管软件技术。而我国自主研发的相关技术较为分散且功能单一（仅开展了力学、流体分析软件的研究），目前还没有一套完整的连续管软件技术，连续管作业设计分析基本依赖于国外连续管软件，同时又由于国内在连续管作业的资源管理、分析、应用方面所做工作滞后明显，导致我国的连续管软件技术的研发与国外相比，存在较大差距。

国外先进的连续管软件主要包括力学、流体和疲劳等3个基本分析模块，开发了安全极限、管柱设计评估、流体参数设计、循环周期、鼓胀/变形预测等设计模块和气举、冲砂、速度管柱等经典工艺设计单元。其中CoilCADE与Tulsa大学合作开发了3项基本分析模型，而经典工艺设计模块是基于现场应用数据积累，不仅仅是基于模型分析。Cerberus的力学和流体分析模型，继承油套管和钢丝绳的分析模型，疲劳分析模型也来自与Tulsa大学的合作；气举、冲砂、速度管柱工艺设计模块是基于流体分析。

国内在连续管基础技术方面缺乏系统研究，目前还未自主建立完善的模型、算法和设计分析流程，其中主要包括3个核心模块的模型与算法和4种典型工艺的设计分析流程：（1）连续管疲劳寿命分析的模型、算法与经典实验数据，连续管缺陷对预测寿命影响的试验方法、模型和经典实验数据；（2）连续管力学分析的模型与算法；（3）连续管流体分析的模型与算法；（4）几种经典工艺的设计分析流程，主要包括气举、冲砂、速度管柱、水平井钻磨桥塞。国内现场连续管作业的井数与国外差距大，导致了经验和数据的积累不足，而且国内连续管软件的研究还处于试验阶段，尚无产品，其中连续管的疲劳寿命刚开始进行试验研究，国内在管柱力学与井筒流体分析上有一定研究基础，但暂时难以用于连续管。

3 模型分类

Model classification

连续管相关软件编制的目的，是对施工工况或参数进行分析，其依据为基本力学模型，要想编制出相关软件，需要详细分析具体施工工况及过程，推导出相关分析模型。因此，通过调研相关模型的实际应用效果，论述各种模型的适应性和选择依据。

3.1 力学分析

Mechanic analysis

目前连续管的力学分析模型主要集中在连续管屈曲行为研究上。1953年，Lubinski［6］通过分析直井中管柱的屈曲问题，得出该条件下的屈曲临界载荷。20世纪60年代，Paslay等［7］利用能量法分析了定向井中管柱的正弦屈曲行为，得出该条件下的初始临界载荷计算模型。70年代，在Lubinski理论的基础上，Hammerlindl［8］对多封隔器管柱和复合管柱进行了屈曲分析，得到了临界载荷，将屈曲理论进行了推广。80年代，Mitchell［9］考虑封隔器对管柱屈曲的影响，利用梁柱方程理论推导出管柱螺旋屈曲的计算模型。90年代，Mitchell［10］考虑径向间距及井斜角的影响，利用数值法推导出定向井中管柱螺旋屈曲的计算模型。1996年，高国华等人［11］通过使用小参数摄动理论和线性化分析方法，得到管柱的正弦屈曲和螺旋屈曲临界载荷。2009年刘昕等［12］利用机械能守恒原理、最小势能原理和拉格朗日乘子法，推导出定向井中摩阻作用下连续管屈曲载荷计算模型。2014年，张超越［13］在充分分析普通连续管井下受力和屈曲状态的基础上，根据弹性细杆的非线性力学，利用静力平衡法，建立了预弯曲连续管井下非线性弯曲的力学模型。2015年，岳欠杯等［14］综合考虑管柱的几何形状（正弦或螺旋屈曲）和管柱屈曲后与井筒的接触摩擦状态，在能量法中引入摩阻损失能与重力势能，采用拉格朗日乘数法描述井筒的滑动位移边界，推导出管柱与井筒之间摩阻力与接触力的计算模型。总体而言，力学分析主要采用经典微分方程法、能量法与有限元法这3种典型的研究方法。

3.2 疲劳预测

Fatigue prediction

目前国际上较为流行的疲劳寿命预测模型有：基于疲劳损伤的Miner模型、Manson-coffin模型和Avakov模型等。1945年，Miner在疲劳累积损伤的理论基础上，通过大量实验研究，提出了Palmgren-Miner线性累积疲劳损伤理论［15］。1952年，Manson等人［16］通过大量实验数据研究，得到疲劳寿命与塑性应变的关系式，即为著名的Manson-Coffin方程，奠定了低周疲劳的基础。1993年，Avakov［17］对连续管进行了疲劳试验，分析表明，由压力引起的静剪切应力分量对连续管疲劳寿命是非线性影响，并提出了等效应变失效准则，推导出连续管疲劳寿命预测模型。

国内方面，2000年，王优强［18］利用等效应力得到了连续管疲劳寿命预测的半经验计算模型。2006年，宋生印［19］基于对连续管周向应力、径向应力、拉应力和等效应力的分析，推导出连续管疲劳寿命预测模型。2008年，王海涛［20］基于三参数幂函数能量法（3SE）与梁弯曲理论，考虑连续管的承载能力，推导出疲劳寿命预测模型，模型的预测精度高于传统的Manson-coffin模型。2012年，李子丰［21］基于脉动循环和对称循环下的疲劳试验数据，用插值法与拟合法推导出预弯曲连续管的疲劳寿命预测模型。2014年，何春生［22］采用能量法推导出了无损和有损伤连续管的疲劳寿命预测模型。总体而言，连续管疲劳预测模型主要是通过Miner理论、经验公式法、应力应变法和三参数幂函数能量法推导而来。国内目前连续管疲劳预测模型有一定的准确度，但还需进行更多的试验和研究。

3.3 流体动力学分析

Fluid mechanics analysis

流体动力学分析的基本力学模型是气液两相管流压降模型。考虑到气液两相流动的复杂性，一般的研究方法是从基本方程出发，利用因次分析、实验等方法来获取特征参数的近似值。因为实验条件和实验设备的差别与限制，半个世纪以来，出现了多种繁简不一、应用范围有限的计算模型。

1963年，Dun和 Ros［23］用 长 10 m，直 径 3.2～14.2 cm的垂直管柱进行了近4 000次的气液两相流动实验，得到了近2万个数据点，总结得出了流态分布图，可应用于垂直井和定向井的相关计算，但不适用于高气液比井（压降梯度偏大）。1965年，Hagedorn和Brown［24］对垂直井中油气水三相流动进行实验研究，并通过反算持液率，得到垂直上升管流的压降计算模型，可适用于小直径管柱。1967年，Orkiszewski［25］分析对比多种气液两相管流压降计算模型，并且使用约150口油井的实测数据综合评价这些模型，提出了4种不同流型下的压降计算模型。1973 年，Beggs和 Brill［26］用空气与水进行实验，通过调节气体流量来观测流型，并测量压力梯度与持液率，提出了适用于定向井与水平井的气液两相管流压降计算模型。1985年，Mukherjee和Brill［27］在Beggs和Brill研究成果的基础上，改进了实验条件，深入研究倾斜管与水平管中气液两相流的流型，建立了更为准确的定向井和水平井两相流流型判别准则与使用便捷的持液率及摩阻因子经验模型。1990年，Ansari等［28］提出描述段塞流、泡状流与环状流流动特性的计算模型，并利用近2 000口油井的实测数据进行检验，与现场实际情况吻合度高。90年代以来，国内外学者陆续提出了许多计算模型，但因为计算复杂且精度不高，油田现场应用较少。总体而言，现有的气液两相管流压降计算模型皆是基于不同实验或现场条件所得，实际应用中还需根据各油田现场测压数据进行评价，优选出合适的气液两相管流压降计算模型。

3.4 速度管柱设计

Velocity string design

3.4.1 设计依据 天然气井通常采用衰竭式开采，纯气藏的最终采收率一般均超过90%，在开采速率和最终采收率上远远超过油藏。但在国内外天然气井的开采过程中，气井积液是最为普遍的现象。一旦出现井底积液，将造成气井产气量的明显下降，严重的积液甚至可以将气井完全压死，最终导致停产。当井筒上返气流量（流速）高于临界携液流量（流速）时，产液气井才能持续携液开采。因此，准确预测气井临界携液流量（流速），对于减少井底积液，提高气井最终采收率具有重要意义。

速度管柱是通过在生产管柱中安装连续管来减少横截面的流动面积，面积减少将导致管柱内气体流速的增大，当管柱底部气体流速大于临界携液流速时，气井井底不产生积液，生产得以恢复。因此，速度管柱的设计依据在于管柱设计合理且实际通过连续管的气体流速需大于气井的临界携液流速［29］。

目前国内外有关临界携液流速的研究较多，主要可分为液滴理论模型和液膜理论模型这两类。1969年，Turner等［30］假设液滴为球形，流型为雾状流，在高气液比和层流条件下，推导出临界携液流速模型，并将计算结果提高了20%。1991年，Coleman等［31-32］将Turner模型应用于其实验数据中，分析认为Turner模型只适合于井口压力小于3.45 MPa，且不应将计算结果提高20%。2000年，Nossier等［33］在Turner等和Coleman等研究成果的基础上，将曳力系数取0.2，把临界携液流速模型的适用范围扩大到过渡流和湍流。2002年，李闽等［34］提出液滴模型应为椭圆形，建立了临界携液流速计算公式，其计算结果仅为Turner模型的1/3。2004年，针对低气液比的气井携液情况，吴志均等［35］以Hagedorn和Brown井筒压力计算方法为基础，定义了理论和实际持液率，建立了确定低气液比临界携液流速的原则和计算公式。2007年，王毅忠等［36］基于球帽状液滴模型，推导出临界携液流速的计算公式。2008年，Belfroid等［37］提出在定向井中使用Turner模型进行计算将会导致较大误差，并结合Fieldler模型和Turner模型，给出定向气井临界携液流速计算模型。2009年，Veeken等［38］研究储层性能和井筒参数对临界流速的影响，并推导出新的计算模型。同年，基于圆球液滴模型，杨文明等［39］提出在定向气井中液滴位于油管中间被携带出井筒，并考虑井斜角的影响，推导出临界气流速计算公式。2010年，基于Turner模型，Zhou等［40］认为除了临界携液流速以外，液体浓度也是确定定向气井携液能力的一个重要指标，指出液滴在井筒中会发生结合，提出液滴结合的临界条件，并推导出新的计算模型。同年，基于魏纳等［41］所做的气井积液可视化实验结果，彭朝阳等［42］以高宽比接近0.9的椭球体液滴为物理模型，考虑液滴内部流动对曳力系数的影响，推导出直井临界携液气流速模型。2010年，肖高棉等［43］对水平井连续携液进行实验研究，得出水平段的液体是以液膜携带为主，而直井段是以液滴携带为主，并推导出水平井临界携液流速模型。同年，雷登生等［44］根据液滴质点分析理论和气液两相雾状流转换准则推导出水平井临界携液流速模型。2011年，于继飞等［45］提出液滴在斜井中是沿着井壁运动，并呈半球形，推导出海上定向气井临界流速的预测方法。2012年，Luan等［46］用损失系数来表示气体能量损失的大小，在李闽模型的基础上，考虑气体举升效率的变化，推导出新的计算模型，在低压情况下，该模型的计算结果要优于Turner模型和李闽模型所计算的结果。同年，李丽等［47］认为液滴在斜井中是沿着井壁运动，并呈圆球形，提出新的临界流速预测方法，并分析了摩擦系数与井斜角对临界流速的影响。2013年，Tan等［48］考虑到湍流条件下，韦伯数法求最大液滴直径不准，而利用液滴平均直径计算模型进行求解，得到新的临界携液流速模型，该模型覆盖全部气液比，并验算得出Turner模型与Coleman模型预测高气液比时误差较大，李闽模型预测低气液比时误差大。2014年，李元生等［49］将水平井分为直井段、定向段和水平段，不同井段采用不同的液滴受力分析模型，推导出不同井段的临界携液流速公式，并将三者中最大值作为水平井的临界携液流速。同年，Luo等［50］考虑管壁不规则液膜厚度，推导出可用于定向井的临界携液流速模型。2015年，宋玉龙等［51］研究临界携液流速沿井筒的分布规律，并通过温度和压力的耦合，推导出随井深变化的计算模型。同年，熊钰等［52］根据质点力平衡理论，考虑液滴变形与尺寸差异的影响，并综合对比曳力系数、液滴变形参数和临界韦伯数之间的函数关系式及计算液滴变形参数的基础上，推导出临界携液流速模型。2016年，基于液膜模型，Chen等［53］通过分析液膜受力情况，推导出定向气井临界携液流速模型，并对油管内径和井斜角进行了敏感性分析。2017年，以液滴沿着井壁上移为物理模型，明瑞卿等［54］考虑过渡流和湍流状态，通过拟合标准阻力曲线，得到曳力系数和雷诺数的关系式，由此推导出定向气井临界携液流速公式，并分析了雷诺数与井斜角对临界流速的影响。

目前国外油田现场应用较多的是Turner模型，而国内主要是运用李闽模型进行预测，但从实际应用效果来看，2个模型在各油田的预测准确度均差异较大，因此，在临界携液流速模型的选择上，应根据各油田现场的实际井况选择合适的计算模型。

3.4.2 设计方法 速度管柱设计的目的是为了找到一个能恢复井筒生产的最优化连续管尺寸和安装深度，以便摩擦损失最小化，产量最大化，而且必须持续生产足够长的时间来抵消速度管柱的安装成本。设计速度管柱时需要比较2种曲线：一种是气井井底流入动态曲线（IPR曲线），另一种是井筒流出动态曲线（“J”曲线）。

IPR曲线完全取决于储层特性，特别是储层压力，与井筒参数无关；“J”曲线表示特定深度、油管尺寸与井口条件下井底流动压力和井筒产气量的关系。“J”曲线被拐点（斜率为0）分为两部分，左边主要受积液压力的影响，右边主要受管道摩擦力影响，临界携液流量也显示在J曲线上（见图2）。

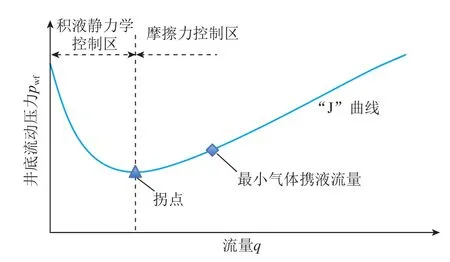
图2 “J”曲线特征示意图Fig. 2 Sketch of J curve characteristic

IPR曲线和“J”曲线交汇处的流速是井筒内气体流速。比较交叉点的流速和“J”曲线上的临界携液流速，会有3种情况发生：（1）气井持续生产，井筒无积液；（2）气井生产一段时间后，因积液严重导致停产；（3）气井一直不生产。

当交叉点在临界点右边，气井持续生产，井筒无积液（图3a）；当交叉点在拐点和临界点中间，气井生产一段时间后，因积液严重导致停产（图3b）；当IPR曲线和“J”曲线不相交或者交点在拐点左边，在特定的管道尺寸、深度和井口压力下，由于井底压力太低，从而导致气井不生产（图3c）。

图3 气井不同生产状态下IPR曲线和“J”曲线示意图Fig. 3 Schematic “J” curve and IPR curve of gas well in different production states

考虑安装速度管柱进行二次完井时，对现有储层的流入特征和井筒的流出特征进行评价非常重要。将未安装速度管柱的“J”曲线与IPR曲线作比较，当井底即将发生积液或已经积液时，就需要安装速度管柱（图4）。

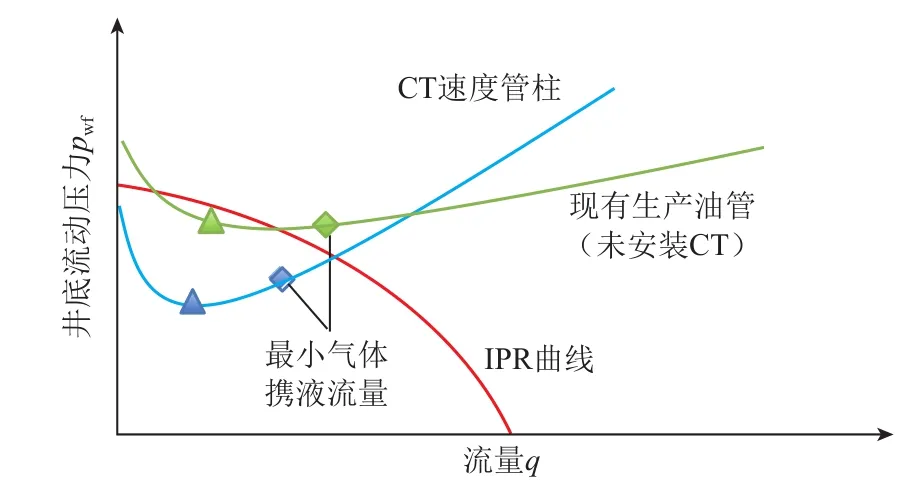
图4 安装速度管柱前后气井生产动态示意图Fig. 4 Schematic production performance of gas well before and after the installation of velocity string

在储层压力持续下降的情况下，速度管柱设计必须能保持井筒的生产时间足够长，才能够抵消安装速度管柱的费用。创建一条IPR曲线来预测未来的储层压力，然后将其与速度管柱“J”曲线作比较，确保未来储层压力下的实际流速大于临界流速，从图5可以看出，速度管柱直径D3最大，当前具有较高产量，但将来会因为积液而停产；直径D1最小，气井能在较低产量下持续生产，主要受摩擦控制；直径D2适中，气井能提高一定的产量并持续生产。设计通常需要在当前生产要求（高产量）和持续生产（相对低的井底压力）之间进行优选，故CT速度管柱直径D2为最佳选择。

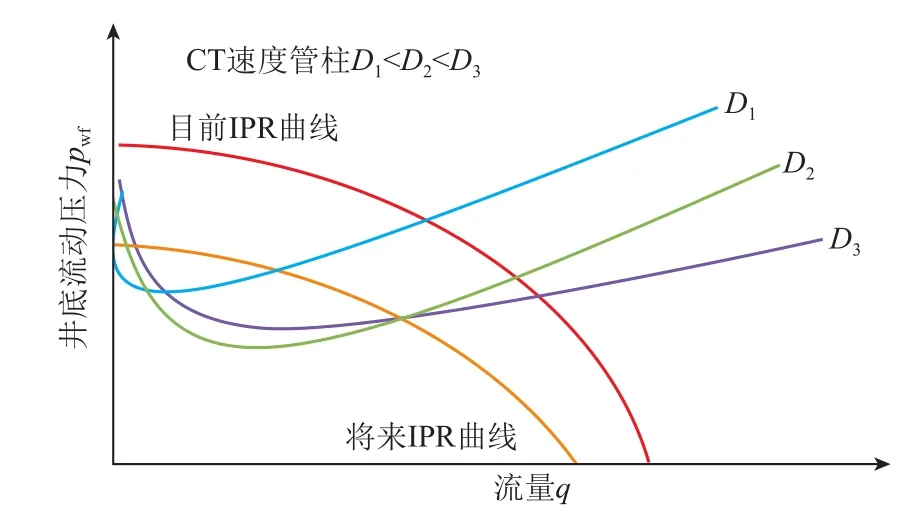
图5 不同尺寸速度管柱气井生产动态示意图Fig. 5 Schematic production performance of gas well with different sizes of velocity string

3.5 钻磨桥塞和冲砂设计

Drilling bridge plug and sand washing design

施工排量是连续管钻磨桥塞及冲砂工艺设计中最重要的参数，不仅涉及到连续管的工作状态、钻磨效率及冲砂效率，还关系到环空返液的携带效果。计算的常用模型有：牛顿-雷廷格模型、莫尔模型、刘希圣模型、斯笃克模型、模拟实验模型、窦国仁模型等［55-57］。在水平井施工作业中，利用连续管进行钻磨桥塞和冲砂时，井底磨屑（砂粒）在上返过程中会经历3个井段，即：直井段、定向段和水平段。直井段一般通过牛顿-雷廷格模型得到最小下沉速度；相关研究证明［58］，钻直井段时，当上返流速大于2倍的磨屑（砂粒）最小下沉速度时，连续管钻磨桥塞（冲砂）过程中的磨屑（砂粒）可上返至地面。定向段一般通过刘希圣岩屑床止动模型得到磨屑（砂粒）的最小止动返速。水平段一般通过窦国仁模型得到磨屑（砂粒）的瞬时起动流速。根据上述模型所得到的计算结果，再通过流体力学中排量计算公式可得到3个井段磨屑（砂粒）上返所需的最小排量。

4 发展方向

Development direction

（1）加快连续管软件数据库的结构设计速度。主要包括标准信息数据库和用户数据库。前者用于存放通用、基础及标准化的数据（连续管属性、流体属性和缺陷属性等）；后者主要用于存放用户收集、采集的数据，以及在实际分析软件运行时生成的数据，包括井身结构、连续管设备（注入头、滚筒、连续管、导向器和防喷盒）、井下工具串、数据采集和在线检测等。

（2）优化连续管软件的整体架构。开发管柱力学、流体力学和疲劳预测3项基本设计分析的软件模块和包含流体参数设计、管柱设计等的设计模块，开发气举、冲砂、速度管柱、钻磨桥塞等典型工艺设计的软件模块，并达到实时监控的可视化，实现设计评估软件的国产化。

（3）研发配套的检测监控系统。国外先进的连续管作业软件，配套开发了丰富的检测监控系统（主要包括数据采集系统、在线检测系统、实时监控与处置系统和井下测控系统），两者相互配套。因此，在开发连续管软件的同时，还应加快检测监控系统的研发速度。

5 结论

Conclusions

（1）国外NOV CTES公司和Schlumberger公司等研发连续管软件已近30年，经验丰富，形成了较为成熟的连续管软件系统，并在持续发展。相比之下，我国研发相关软件功能单一、体系分散，与国外连续管软件水平的差距呈扩大趋势。

（2）目前自主研发的连续管装备与工具在国内已规模化应用，但对连续管软件一直未开展系统的研究，由于其长期依赖进口，严重制约了连续管技术的进一步发展，因此，为进一步提高效率、增进安全，持续推进国内连续管技术的发展，研发出满足油田现场需求、具有自主知识产权的连续管软件势在必行。

［1］王伟佳. 连续油管光纤测井技术及其在页岩气井中的应用［J］. 石油钻采工艺，2016，38（2）：206-209.

WANG Weijia. Well logging via coiled tubing fiber optic infrastructures and its application in shale gas wells［J］.Drilling & Production Technology, 2016, 38（2）: 206-209.

［2］席仲琛，徐迎新，曹欣. 水平井油管钻磨复合桥塞技术及应用［J］. 石油钻采工艺，2016，38（1）：123-127.

XI Zhongchen, XU Yingxin, CAO Xin. Composite bridge plug drilling and milling technology by tubing in horizontal well and its application［J］. Drilling &Production Technology, 2016, 38（1）: 123-127.

［3］王安义，龙尧，蔡科涛，吴大飞，刘云见，白兰昌. 井下连续管力学行为分析软件及应用［J］. 石油机械，2011，39（6）：47-49.

WANG Anyi, LONG Yao, CAI Ketao, WU Dafei,LIU Yunjian, BAI Lanchang. Software for mechanical behavior analysis of downhole coiled tubing［J］. China Petroleum Machinery, 2011, 39（6）: 47-49.

［4］管锋，马卫国，周传喜，徐健，夏忠伟. 连续管钻井水力参数计算软件开发［J］. 石油机械，2014，42（3）：29-32.

GUAN Feng, MA Weiguo, ZHOU Chuanxi, XU Jian,XIA Zhongwei. Development of the hydraulic parameter calculation software for coiled tubing drilling［J］. China Petroleum Machinery, 2014, 42（3）: 29-32.

［5］练波，练章华，程文，邹先雄. 连续管流体特性参数分析软件开发及应用［J］. 石油机械，2015，43（7）：80-83.

LIAN Bo, LIAN Zhanghua, CHEN Wen, ZOU Xianxiong.Analysis software for characteristic parameters of fluids in coiled tubing［J］. China Petroleum Machinery, 2015, 43（7）: 80-83.

［6］LUBINSKI A. A study of the bucking of rotary drilling string［C］. Drilling and Production Practice, 1950: 178-214.

［7］PASLEY P R, BOGY D B. The stability of a cireular rod laterally constrained to be in contact with an inclined circular cylinder［J］. Journal Applied Mechanics, 1964,31（4）: 605-610.

［8］HAMMERLINDL D J. Movement, forces and stresses associated with combination tubing strings sealed in packers［J］. Journal of Petroleum Technology, 1977, 29（1）: 195-208.

［9］MITCHELL R F. New concepts for helical buckling［R］.SPE 15470, 1986.

［10］MITCHELL R F. Buckling analysis in deviated wells:a practical method［J］. SPE Drilling & Completion,1996, 14（1）: 11-20.

［11］高国华，李琪，李淑芳. 管柱在水平井眼中的屈曲分析［J］. 石油学报，1996，17（3）：123～129.GAO Guohua, LI Qi, LI Shufang. A Buckling analysis of pipe string in horizonal boreholes ［J］. Acta Petrolei Sinica, 1996, 17（3）: 123-129.

［12］刘昕，练章华，罗宇灿，谭清明，房皓. 井壁接触应力影响下的连续油管屈曲载荷计算方法［J］. 西部探矿工程，2009，21（4）：116-119.

LIU Xin, LIAN Zhanghua, LUO Yucan, TAN Qingming,FANG Hao. Calculation method of coiled tubing buckling load under the influence of well wall contact stress［J］. West-China Exploratin Engineering, 2009,21（4）: 116-119.

［13］张超越. 预弯曲连续油管井下稳定性分析［D］. 秦皇岛：燕山大学，2013.

ZHANG Chaoyue. The Stability Analysis of Pre-bending Coiled Tubing in The Downhole［D］. Qinhuangdao:Master Thesis of Yanshan University, 2013.

［14］岳欠杯，刘巨保，付茂青. 井筒内受压杆管后屈曲能量法分析与实验研究［J］. 力学与实践，2015，37（6）：713-718.

YUE Qianbei, LIU Jubao, FU Maoqing. The energy method and experimental study of post-buckling of the pressurized rod string in wellbore［J］. Mechanics in Engineering, 2015, 37（6）: 713-718.

［15］程文. 连续油管力学特性分析与疲劳寿命研究［D］.成都：西南石油大学，2016.

CHENG Wen. Study on mechanical properties and fatigue life of coiled tubing［D］. Chengdu: Southwest Petroleum University, 2016.

［16］COLLINS J A. Failure of materials in mechanical design:analysis Prediction Prevention ［C］. New York: J Wiley,1981.

［17］AVAKOV V A, FOSTER J C, SMITH E J. Coiled tubing life prediction［R］. OTC 7325, 1993.

［18］王优强，张嗣伟. 连续油管疲劳可靠性分析的新方法［J］. 石油机械，2000，28（1）：5-8.

WANG Youqiang, ZHANG Siwei. A new method for fatigue reliability analysis of coiled tubing［J］. China Petroleum Machinery, 2000, 28（1）: 5-8.

［19］宋生印，王英杰，林元华，张德平. 连续管疲劳寿命预测［J］. 煤田地质与勘探，2006，34（6）：73-76.

SONG Shengyin, WANG Yingjie, LIN Yuanhua,ZHANG Deping. Fatigue life prediction of coiled tubing［J］. Coal Geology & Exploration, 2006, 34（6）: 73-76.

［20］王海涛，李相方. 连续油管卷曲低周疲劳寿命预测［J］.石油机械，2008，36（11）：25-27.

WANG Haitao, LI Xiangfang. Low cycle bending fatigue life prediction of coiled tubing［J］. China Petroleum Machinery, 2008, 36（11）: 25-27.

［21］李子丰，李雪娇，王鹏. 预弯曲连续油管及其疲劳寿命预测［J］. 石油学报，2012，33（4）：706-710.

LI Zifeng, LI Xuejiao, WANG Peng. Pre-bending coiled tubing and its fatigue life prediction［J］. Acta Petrolei Sinica, 2012, 33（4）: 706-710.

［22］何春生，刘巨保，岳欠杯，李伟权. 基于椭圆度及壁厚参数的连续油管低周疲劳寿命预测［J］. 石油钻采工艺，2013，35（6）：15-18.

HE Chunsheng, LIU Jubao, YUE Qianbei, LI Weiquan.Prediction of the low-cycle fatigue life of the coiled tubing based on ovality and wall thickness parameter［J］. Drilling & Production Technology, 2013, 35（6）:15-18.

［23］DUNS H Jr, ROS N C J. Vertical flow of gas and liquid mixtures in wells［C］. Presented at 6th World Petroleum Congress, 19-26 June 1963, Frankfurt, Germany.

［24］HAGEDORN A R, BROWN K E. Experimental study of pressure gradients occurring during continuous twophase flow in small-diameter vertical conduits［J］.Journal of Petroleum Technology, 1965, 17（4）: 475-484.

［25］ORKISZEWSKI J. Predicting two-phase pressure drops in vertical pipe［J］. Journal of Petroleum Technology,1967, 19（6）: 829-838.

［26］BEGGS D H, BRILL J P. An experimental study of twophase flow in inclined pipes［J］. Journal of Petroleum Technology, 1973, 25（5）: 607-617.

［27］MUKHERJEE H, BRILL J P. Pressure drop correlations for inclined two-phase flow［J］. Journal of Energy Resources Technology, 1985, 107（4）: 549-554.

［28］ANSARI A M, SYLVESTER, SHOHAM O, BRILL J P. A comprehensive mechanistic model for upward twophase flow in wellbores ［R］. SPE 20630, 1990.

［29］王海涛，李相方. 气井CT速度管柱完井技术理论研究［J］. 石油钻采工艺，2009，31（6）：41-45.

WANG Haitao, LI Xiangfang. Theoretical study on coiled tubing velocity string completion technique in gas wells［J］. Oil Drilling & Production Technology, 2009,31（6）: 41-45.

［30］TURNER R G, HUBBARD M G, DUKLER A E.Analysis and prediction of minimum flow rate for the continuous removal of liquids from gas wells ［J］.Journal of Petroleum Technology, 1969, 21（11）: 1475-1482.

［31］COLEMAN S B, CLAY H B, MCCURDY D G. A new look at predicting gas-well load-up［J］. SPE Journal of Petroleum Technology, 1991, 43（3）: 329-333.

［32］COLEMAN S B, CLAY H B, MCCURDY D G.Understanding gas-well load-up behavior［J］. SPE Journal of Petroleum Technology, 1991, 43（3）: 334-338.

［33］NOSSEIR M A, DARWICH T A, SAYYOUH M H. A new approach for accurate prediction of loading in gas wells under different flowing conditions［R］. SPE 37408, 1997.

［34］LI M, LI S L, SUN L T. New view on continuousremoval liquids from gas wells［J］. SPE Production &Operations, 2002, 17（1）: 42-46.

［35］吴志均，何顺利. 低气液比携液临界流量的确定方法［J］. 石油勘探与开发，2004，31（4）：108-114.

WU Zhijun, HE Shunli. Determination of the critical liquid carrying flow rate at low gas liquid ratio［J］.Petroleum Exploration and Development, 2004, 31（4）:108-114.

［36］王毅忠，刘庆文. 计算气井最小携液临界流量的新方法［J］. 大庆石油地质与开发，2007，26（6）：82-85.

WANG Yizhong, LIU Qingwen. A new method to calculate the minimum critical liquids carrying flow rate for gas wells［J］. Petroleum Geology & Oilfield Development in Daqing, 2007, 26（6）: 82-85.

［37］BELFROID S P C, SCHIFERLI W, ALBERTS G J N, VEEKEN C A M, Biezen E. Prediction onset and dynamic behaviour of liquid loading gas wells［R］.SPE 115567, 2008.

［38］VEEKEN K, HU B, SCHIFERLI W. Transient multiphase flow modeling of gas-well liquid loading［R］. SPE 123657, 2009.

［39］杨文明，王明，陈亮，吴进超，余鹏翔. 定向气井连续携液临界产量预测模型［J］. 天然气工业，2009，29（5）：82-84.

YANG Wenming, WANG Ming, CHEN Liang, WU Jinchao, YU Pengxiang. A prediction model on calculation of continuous liquid carrying critical production of directional gas wells［J］. Natural Gas Industry, 2009, 29（5）:82-84.

［40］ZHOU D, YUAN H. A new model for predicting gaswell liquid loading［J］. SPE Production & Operations,2010, 25（2）: 172-181.

［41］魏纳，李颖川，李悦钦，刘安琪，廖开贵，喻欣. 气井积液可视化实验［J］. 钻采工艺，2007，30（3）：43-45.

WEI Na, LI Yingchuan, LI Yueqin, LIU Anqi, LIAO Kaigui, YU Xin. Visual experimental research on gas well liquid loading［J］. Drilling and Production Technology, 2007, 30（3）: 43-45.

［42］彭朝阳. 气井携液临界流量研究［J］. 新疆石油地质，2010，31（1）：72-74.

PENG Chaoyang. Study on critical liquid-carrying flow rate for gas well［J］. Xinjiang Petroleum Geology,2010, 31（1）: 72-74.

［43］肖高棉，李颖川，喻欣. 气藏水平井连续携液理论与实验［J］. 西南石油大学（自然科学版），2010，32（3）：122-126.

XIAO Gaomian, LI Yingchuan, YU Xin. Theory and experiment research on the liquid continuous removal of horizontal gas well［J］. Journal of Southwest Petroleum University（Science & Technology Edition）,2010, 32（3）: 122-126.

［44］雷登生，杜志敏，单高军，汤勇，李涧松，付玉. 气藏水平井携液临界流量计算［J］. 石油学报，2010，31（4）：637-639.

LEI Dengsheng, DU Zhimin, SHAN Gaojun, TANG Yong, LI Jiansong, FU Yu. Calculation method for critical flow rate of carrying liquid in horizontal gas well［J］. Acta Petrolei Sinica, 2010, 31（4）: 637-639.

［45］于继飞，管虹翔，顾纯巍，齐桃，李伟超. 海上定向气井临界流量预测方法［J］. 特种油气藏，2011，18（6）：117-119.

YU Jifei, GUAN Hongxiang, GU Chunwei, QI Tao, LI Weichao. Prediction of critical flow rate for offshore directional gas wells［J］. Special Oil & Gas Reservoirs, 2011, 18（6）: 117-119.

［46］LUAN G, HE S. A new model for the accurate prediction of liquid loading in low-pressure gas wells［J］. Journal of Canadian Petroleum Technology, 2012, 51（6）: 493-498.

［47］李丽，张磊，杨波，殷茵，李登伟. 天然气斜井携液临界流量预测方法［J］. 石油与天然气地质，2012，33（4）：650-654.

LI Li, ZHANG Lei, YANG Bo, YIN Yin, LI Dengwei.Prediction method of critical liquid-carrying flow rate for directional gas wells［J］. Oil & Gas Geology, 2012, 33（4）: 650-654.

［48］TAN H X, LI X P, LIU J Y. Model of continuous liquid removal from gas wells by droplet diameter estimation［J］. Journal of Natural Gas Science and Engineering,2013, 15: 8-13.

［49］李元生，李相方，藤赛男，刘晓东，徐大融，任美鹏. 气井携液临界流量计算方法研究［J］. 工程热物理学报，2014，35（2）：292-294.

LI Yuansheng, LI Xiangfang, TENG Sainan, LIU Xiaodong, XU Darong, REN Meipeng. Research of gas well liquid-carrying critical rate model［J］. Journal of Engineering Thermophysics, 2014, 35（2）: 292-294.

［50］LUO S, KELKAR M, PEREYRA E, SARICA C. A new comprehensive model for predicting liquid loading in gas wells［J］. SPE Production & Operations, 2014, 29（4）:337-349.

［51］宋玉龙，杨雅惠，曾川，丁磊，赵润东，袁玥. 临界携液流量与流速沿井筒分布规律研究［J］. 断块油气田，2015，22（1）：90-93.SONG Yulong, YANG Yahui, ZENG Chuan, DING Lei,ZHAO Rundong, YUAN Yue. Research on distribution of critical carrying fluid flow rate and velocity along shaft［J］. Fault-Block Oil and Gas Field, 2015, 22（1）:90-93.

［52］熊钰，张淼淼，曹毅，鲜波，卢怡. 一种预测气井连续携液临界条件的通用模型［J］. 水动力研究与进展，2015，30（2）：215-222.

XIONG Yu, ZHANG Miaomiao, CAO Yi, XIAN Bo,LU Yi. A universal model of prediction for critical continuous removal of liquids from gas wells［J］.Chinese Journal of Hydrodynamics, 2015, 30（2）: 215-222.

［53］CHEN D C, YAO Y, FU G, MENG H X, XIE S X. A new model for predicting liquid loading in deviated gas wells［J］. Journal of Natural Gas Science and Engineering,2016, 34: 178-184.

［54］MING R Q, HE H Q. A new approach for accurate prediction of liquid loading of directional gas wells in transition flow or turbulent flow［J］. Journal of Chemistry. 2017（4）: 1-9.

［55］逢仁德，崔莎莎，韩继勇，罗晶晶，刘亚飞，陈军伟. 水平井连续油管钻磨桥塞工艺研究与应用［J］. 石油钻探技术，2016，44（1）：57-62.

FENG Rende, CUI Shasha, HAN Jiyong, LUO Jingjing,LIU Yafei, CHEN Junwei. Research and application of drilling milling-grinding techniques for drilling out composite bridge plugs in coiled tubing in horizontal wells［J］. Petroleum Drilling Techniques, 2016, 44（1）:57-62.

［56］沈燕来，陈建武. 冲砂洗井水力计算方法综述［J］.水动力学研究与进展，1998，13（3）：347-353.

SHEN Yanlai, CHEN Jianwu. Brief review on hydraulic calculation methods of sand flushing［J］. Chinese Journal of Hydrodynamics, 1998, 13（3）: 347-353.

［57］曲洪娜，黄中伟，李根生，夏强，宋先知，王海柱. 水平井旋转射流冲砂洗井水力参数设计方法［J］. 石油钻探技术，2011，39（6）：39-43.

QU Hongna, HUANG Zhongwei, LI Gensheng, XIA Qiang, SONG Xianzhi, WANG Haizhu. Hydraulic parameters of sand-flushing with rotating jets in horizontal wells［J］. Petroleum Drilling Techniques,2011, 39（6）: 39-43.

［58］赖枫鹏，李治平，芩芳，黄志文，许进进. 水平井水力冲砂最优工作参数计算［J］. 石油钻探技术，2007，35（1）：69-71.

LAI Fengpeng, LI Zhiping, CEN Fang, HUANG Zhiwen, XU Jinjin. Optimum working parameters for hydraulic sand washing in horizontal wells［J］.Petroleum Drilling Techniques, 2007, 35（1）: 69-71.