非稳态渗流下砂砾岩水力裂缝扩展数值模拟

张红静 徐康泰 刘立冬 吴德 高秀君 孙春亮 李立

1.承德石油高等专科学校；2.中国石油渤海钻探工程有限公司；3.中国石油华北油田分公司；4.濮阳佰斯泰油气技术有限公司

水力压裂过程是一个渗流场与应力场耦合的复杂结果，由于地面高压流体的注入，围岩的应力场重新分布，使得岩体裂缝开裂、扩展；同时裂缝的规模、空间展布特征及裂缝面的物理力学性质影响流体渗流作用。Detournay等［1］考虑流-固耦合现象，分析了水力压裂过程中流-固耦合的必要性。薛炳等［2］利用ABAQUS有限元分析软件，考虑渗流应力耦合现象，采用cohesive单元，建立水力压裂的有限元数值模型。李林地等［3］应用损伤力学方法，建立了碳酸盐岩储层水力裂缝扩展数学模型，模拟稳定渗流场、应力场和温度场多物理场下裂缝扩展问题。余东合等［4］运用细观有限元的方法，完成砂砾岩储层水力裂缝扩展数值模拟研究，但其只在稳定渗流条件下，分析了水力裂缝与砾石相遇时的形态，与实际地层流体流动差别较大。砾石由基质—交界面—砾石构成，砾石分布和形态性质具备一定的随机分布函数特征，结合损伤力学方法［5-6］，在应力场与非稳定渗流场耦合作用下，建立了砂砾岩储层水力裂缝扩展的数学模型。利用该模型分析了应力场、砾石粒径大小和砾石含量对裂缝扩展的影响，并分析了不同情况下岩体起裂压力。

1 砂砾岩裂缝扩展数学模型的建立

Establishment of mathematical model for fracture propagation in glutenite

1.1 砂砾岩储层砾石表征

Characterization of gravels in glutenite reservoir

准确的砾石数学表征是砂砾岩储层水力裂缝模拟的基础［4］。考虑“基质—交界面—砾石” 的复合结构［7］，并使得砾石几何形态参数及其储层中的分布符合一定的随机函数［8-9］，主要包括砾石的粒径大小和砾石中心点在区域的分布。

（1）砾石粒径l。设砾石粒径l服从正态分布，则

式中，μ为粒径l的均值，m；σ为粒径l的均方差，m。（2）砾石中心点坐标（x0，y0）。设中心点位置（x0，y0）服从均匀分布，则

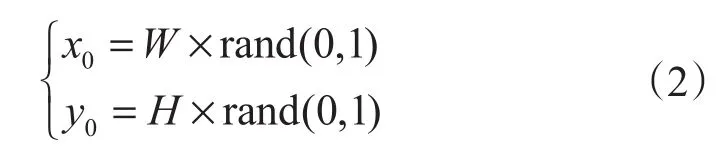
式中，W为研究区域长，m；H为研究区域宽，m；rand（0，1） 为（0，1）内的伪随机数。

按照Monte-Carlo模拟实现参数的随机抽样，从生成的粒径和中心点位置中完成抽样

式中，F（x）为分布函数；XF为由已知分布函数F（x）所产生的简单子样X1，X2，…，XN中的个体；ξ为伪随机序列ξ1，ξ2，…，ξN中的对应伪随机数。

1.2 数学模型

Mathematical model

运用断裂力学原理，考虑非稳定渗流—应力耦合效应［10-11］，建立砂砾岩储层非稳定渗流场［12］下的水力压裂裂缝扩展数学模型。

（1）渗流方程。

式中，p为流体压力，MPa；η为导压系数，；k为渗透率，mD；ϕ为孔隙度；μ为流体黏度，Pa·s；Ct为综合压缩系数。

（2）平衡方程。

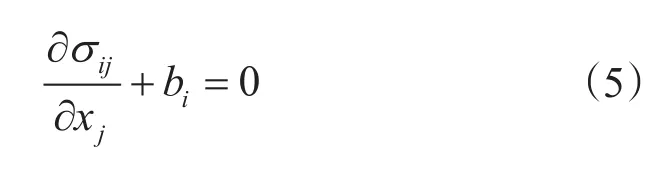
式中，σij为应力，MPa；bi为体积力，MPa；i，j为张量下标，i=1，2，j=1，2。

根据式（4）、式（5），构建耦合问题的本构方程，该方程考虑了初始应力和流体压力项

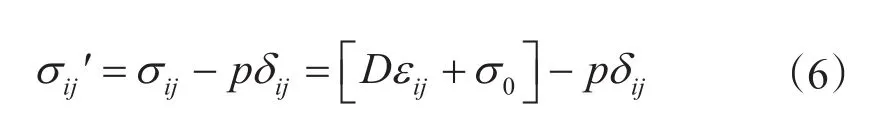
式中，σij′为有效应力，MPa；σ0为初始地应力，MPa；δij为Kronecker常数；D为弹性矩阵；εij为应变，；u为位移，m。

2 模型的求解

Solution

2.1 非稳态渗流方程求解

Solution of unsteady seepage equation

根据式（6）解决该问题的本构方程，可知关键在于求解不同时刻渗流场压力值。取试探函数，其中n为总结点数，应用Galerkin法，由式（4）可得

应用Geren-Gauss公式，可将式（7）变换成如下形式

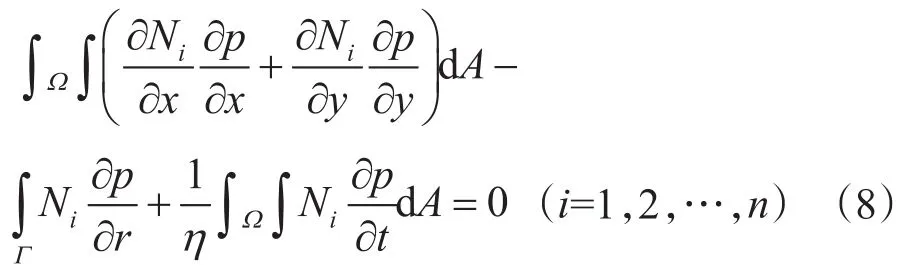
式（8）即为本文考虑的平面不稳定渗流问题的基本方程，其中Γ为Ω的边界。

利用平面三角形单元，进一步可写出单元内的积分形式

最终可表示为

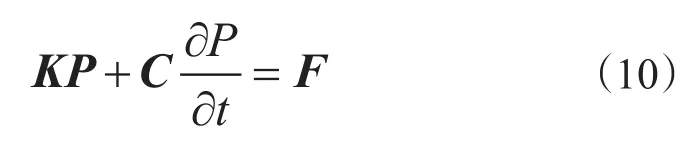
式中，Ni为形函数，；Ω为积分区域；i，j，m为三角形单元边界点；s为单元边界长度；A为围成的单元格面积；Ni，Nj，Nm为三点插值形函数；K为总体刚度矩阵；C为变温矩阵；F为等式右端项组成的列向量；P为结点压力值的列向量。

由式（10）即可求解不稳定渗流场压力的问题，并将每一时间步下求解的结果代到式（6）单元本构方程中，求解单元的整体应力大小。设定较小时间步长，得到单元应力，在某时刻岩体初始位置单元开始破裂，定义此时该单元处应力为破裂压力。

2.2 时间处理问题

Time processing

式（10）采用加权余量法建立两点循环公式，求解不同时间下的渗流场。

将时间也分成若干单元，利用差值函数Ni（t），将任意时间P（t）表示为

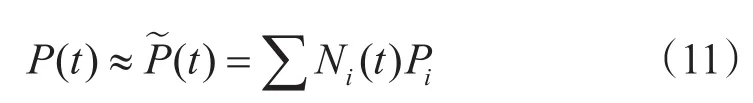
式中，Pi是在时刻i时的P（t）一组结点值；向量P中每个分量都取相同形式的函数。

取任意时间步长Δt，得到压力P（t）在时间节点上的关系

针对式（12），设定某局部变量ζ和基本加权参数w，完成加权余量格式

根据插值函数及其一阶导数，将式（13）表示为

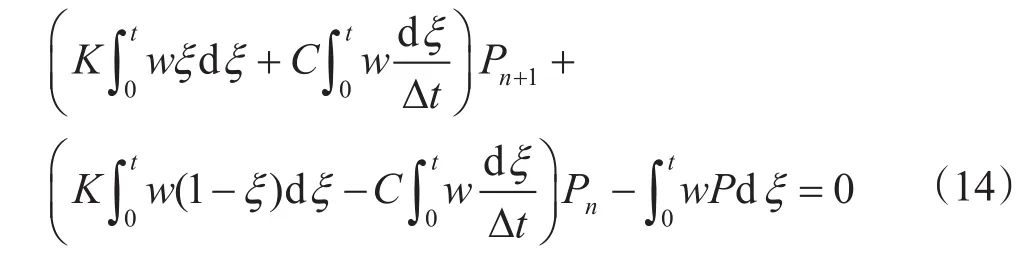
由式（14）建立时间步Δt内Pn与Pn+1的关系，继而将整个时间域分为若干时间步长，以此递推求得各个时间下的渗流压力值。

3 砂砾岩裂缝扩展数值模拟结果与分析

Numerical simulation result of fracture propagation in glutenite and its analysis

建立了用于分析砂砾岩储层水力压裂裂缝扩展的数学模型，重点考虑不稳定渗流条件下，完成模型的求解问题，并利用Matlab编程实现数值模拟研究。建立水力裂缝扩展基本模型，模型尺寸1 000 mm×1 000 mm，砾石粒径15 mm，砾石含量75%，围压30 MPa，排量0.03 m3/s，施工时间1200 s，时间步长为1 s，地层最大、最小主应力分别为 45 MPa、30 MPa，原始地层压力25 MPa。其余参数见表1。

表1 模型物理力学参数Table 1 Physical mechanic parameters of the model

利用该模型，完成数值模拟分析，如图1所示。

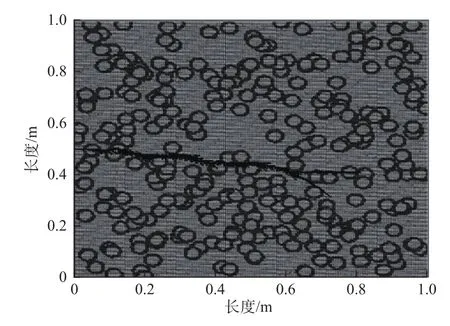
图1 砂砾岩储层水力压裂裂缝扩展形态Fig. 1 Propagation morphology of hydraulic fractures in glutenite reservoir

由图1可以清晰地观察到裂缝扩展形态和遇砾形态，得知：砂砾岩储层水力压裂裂缝延伸过程中，当水力裂缝与砾石相遇时，主要发生穿砾、绕砾、止裂等情况，并以绕砾扩展为主；水力裂缝扩展路径中，存在大量的分支缝，羽状次生裂缝发育。

4 砂砾岩裂缝扩展影响因素分析

Analysis on the factors influencing the fracture propagation in glutenite

根据本文建立的数学模型，完成砂砾岩储层水力压裂裂缝扩展影响因素研究，分析不同主应力差、砾石粒径大小与砾石含量对水力裂缝扩展的影响，并得到不同情况下岩体破裂压力变化情况，基本模型参数见表1。其中，岩体破裂压力得到方法如下：逐步加大注入排量，直到起裂处单元破坏，通过单元应力计算公式（6），得到单元破坏时单元应力值，即为岩体破裂压力。

4.1 主应力差

Principle stress difference

设定主应力差值为 5、15、20、25 MPa，模拟结果如图2。可以看出：（1）随着主应力差的增大，裂缝半长增大，这种趋势随着应力差的进一步增大而减缓；由于较大的主应力使得裂缝遇砾不易发生偏转，整体裂缝形态较好，能量损耗减少，裂缝在最大主应力方向上的延伸长度较大；（2）储层主应力差越大，岩体破裂压力呈现增大的趋势。

图2 不同主应力差对破裂压力和裂缝半长的影响Fig. 2 Effect of principal stress difference on fracturing pressure and half fracture length

4.2 砾石粒径

Gravel particle diameter

在相同砾石含量下，粒径设定为0.01、0.02、0.03、0.04 m。模拟结果如图 3。可以得到：（1）随砾石粒径增大，水力裂缝的延伸长度呈递增趋势；由于砾石含量不变，砾石粒径越大，模拟条件下水力裂缝遇砾的机会将越小，裂缝转向越不明显，耗能越少，裂缝越长；（2）砾石越大，岩体破裂压力越小，相差幅度不大。

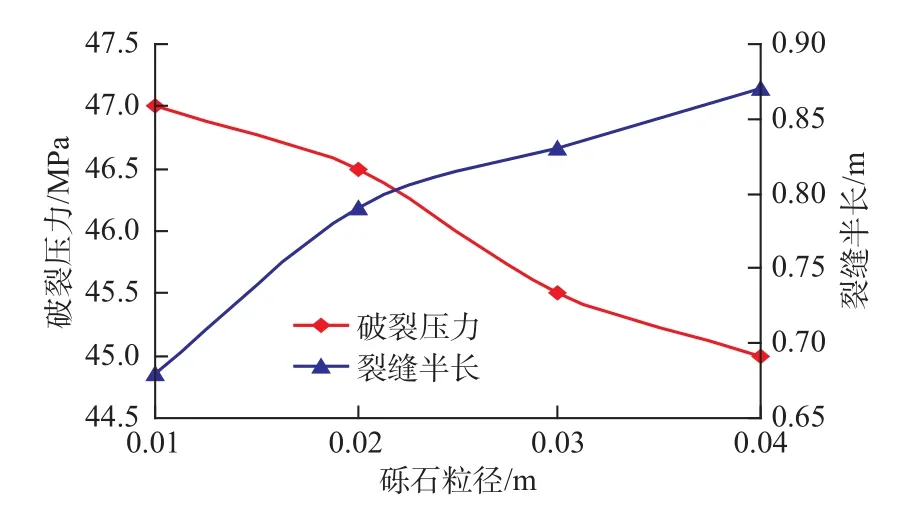
图3 不同砾石粒径对破裂压力和裂缝半长的影响Fig. 3 Effect of gravel particle diameter on fracturing pressure and half fracture length

4.3 砾石含量

Gravel content

取砾石含量分别为30%、45%、60%、75%，模拟结果如图4。可以看出：（1）砾石含量越大，水力裂缝遇砾几率越大，耗能越多，水力裂缝的延伸长度越小，但这种程度呈递减趋势；（2）砾石的强度大于基质的强度，砾石含量越大，岩体体系的力学性质越趋向于砾石，岩体的破裂压力也呈增大的趋势。

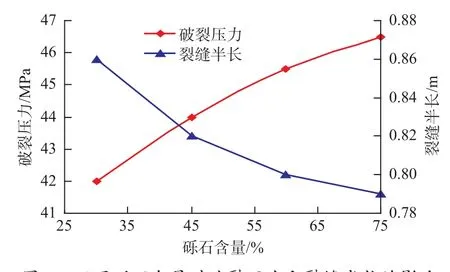
图4 不同砾石含量对破裂压力和裂缝半长的影响Fig. 4 Effect of gravel content on fracturing pressure and half fracture length

4.4 排量

Flow rate

设定排量分别为 0.025、0.03、0.035、0.04 m3/s，模拟结果见图5所示。

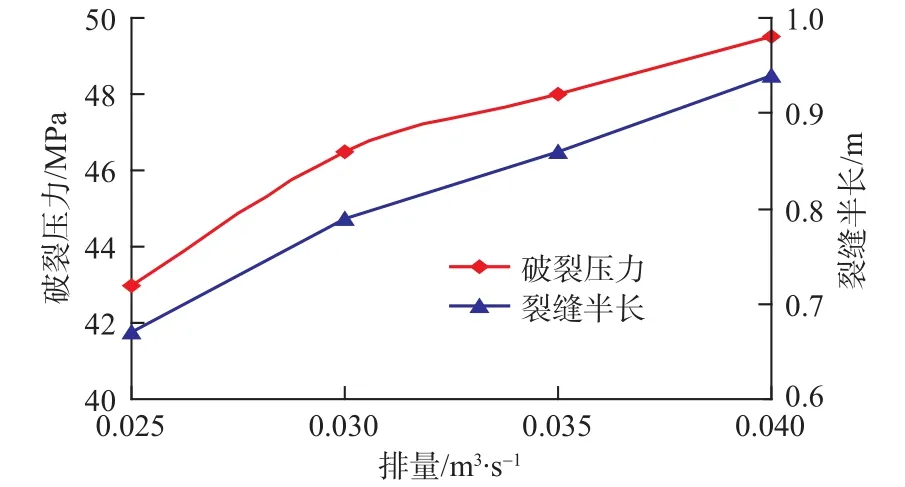
图5 不同排量对破裂压力和裂缝半长的影响Fig. 5 Effect of flow rate on fracturing pressure and half fracture length

由图5可以看出：（1）排量越大，相同时间内外界给予能量越多，水力裂缝的延伸长度越大；（2）瞬间给予的排量增大，瞬时压力上升，岩体破裂压力也呈增大的趋势。

5 结论

Conclusio ns

（1）运用断裂力学与损伤力学的方法，建立了应力场与非稳定渗流场共同作用下的砂砾岩储层水力裂缝扩展的数学模型。模拟结果表明：砾石存在影响水力裂缝扩展，不同于常规储层压裂，水力裂缝遇砾发生绕砾、穿砾与止裂现象，并以绕砾扩展为主；裂缝形态复杂，并伴有次生羽状裂缝产生。

（2）砂砾岩储层水力裂缝延伸长度受主应力差、砾石粒径与砾石含量的影响：在相同条件下，主应力差、砾石粒径、排量增大，砾石含量减小、裂缝长度均呈现递增趋势。

（3）砂砾岩储层水力压裂岩体起裂压力受主应力差、砾石粒径与砾石含量的影响：在相同条件下，随着主应力差、砾石含量、排量增大、砾石粒径减小，岩体破裂压力呈增大趋势。

References:

［1］DETOURNAY E, McLENNAN J D, ROEGIERS J C. Poroelastic concepts explain some of the hydraulic fracturing mechanism［R］. SPE 15262, 1986.

［2］薛炳，张广明，吴恒安，王秀喜. 油井水力压裂的三维数值模拟［J］. 中国科学技术大学学报，2008，38（11）：1322-1325.

XUE Bing, ZHANG Guangming, WU Hengan, WANG Xiuxi. Three-dimensional numerical simulation of hydraulic fracture in oil wells ［J］. Journal of University of Science & Technology China, 2008, 38（11）: 1322-1325.

［3］李林地，张士诚，张劲，潘林华. 缝洞型碳酸盐岩储层水力裂缝扩展机理［J］. 石油学报，2009，30（4）：570-573.

LI Lindi, ZHANG Shicheng, ZHANG Jin, PAN Linhua.Mechanism of hydraulic fracture propagation in fracturecavity carbonate reservoirs［J］. ACTA Petrolei Sinica,2009, 30（4）: 570-573.

［4］余东合，徐康泰，车航，张登文，刘国华，马新仿. 基于细观损伤多相耦合的砂砾岩水力压裂裂缝扩展数值模拟［J］. 石油钻采工艺，2016，38（3）：352-358.

YU Donghe, XU Kangtai, CHE Hang, ZHANG Dengwen,LIU Guohua, MA Xinfang. Numerical simulation on hydraulic fracture propagation in glutenite reservoir based on microscopic damage multiphase coupling［J］. Oil Drilling & Production Technology, 2016, 38（3）: 352-358.

［7］刘红岩，吕淑然，张力民. 基于组合模型法的贯通节理岩体动态损伤本构模型［J］. 岩土工程学报，2014，36（10）：1814-1821.

LIU Hongyan, LV Shuran, ZHANG Limin. Dynamic damage constitutive model for persistent jointed rock mass based on combination model method［J］. Chinese Journal of Geotechnical Engineering, 2014, 36（10）: 1814-1821.

［8］LU Xinzheng, XIE Linlin, GUAN Hong, HUANG Yuli,LU Xiao. A shear wall element for nonlinear seismic analysis of super-tall buildings using OpenSees［J］.Finite Elements in Analysis & Design, 2015, 98: 14-25.

［9］杜修力，金浏. 考虑过渡区界面影响的混凝土宏观力学性质研究［J］. 工程力学，2012，29（12）：72-79.

DU Xiuli, JIN Liu. Research on the influence of interfacial transition zone on the macro-mechanical properties of concrete ［J］. Engineering Mechanics, 2012, 29（12）: 72-79.

［10］杨明辉，赵明华，曹文贵. 岩石损伤软化统计本构模型参数的确定方法［J］. 水利学报，2005，36（3）：345-349.

YANG Minghui, ZHAO Minghua, CAO Wengui.Method for determining the parameters of statistical damage softening constitutive model for rock［J］.Journal of Hydraulic Engineering, 2005, 36（3）: 345-349.

［11］梁正召，杨天鸿，唐春安，张娟霞，唐世斌，于庆磊. 非均匀性岩石破坏过程的三维损伤软化模型与数值模拟［J］. 岩土工程学报，2005，27（12）：1447-1452.

LIANG Zhengzhao, YANG Tianhong, TANG Chunan, ZHANG Juanxia, YU Qinglei. Threedimensional damage soften model for failure process of heterogeneous rocks and associated numerical simulation［J］. Chinese Journal of Geotechnical Engineering,2005, 27（12）: 1447-1452.

［12］ZHOU J, JIANG J, CHEN X. Micro- and macroobservations of liquefaction of saturated sand around buried structures in centrifuge shaking table tests［J］.Soil Dynamics & Earthquake Engineering, 2015, 72（5）:1-11.

［13］BAI Y L, WANG H Y, XIA M F, KE F J. Statistical mesomechanics of solid liking coupled multiple space and time scales［J］. Applied Mechanics Reviews,2005, 58（6）: 372-388.

［16］李军诗，侯建锋，胡永乐，李凡华，秦强. 压裂水平井不稳定渗流分析［J］. 石油勘探与开发，2008，35（1）：92-96.

LI Junshi, HOU Jianfeng, HU Yongle, LI Fanhua, QING Qiang. Performance analysis of unsteady porous flow in fractured horizontal wells［J］. Petroleum Exploration and Development, 2008, 35（1）: 92-96.