智能配电网故障指示器优化配置研究

姜 健 鲍光海

（福州大学电气工程与自动化学院，福州 350116）

智能配电网故障指示器优化配置研究

姜 健 鲍光海

（福州大学电气工程与自动化学院，福州 350116）

为了实现故障指示器经济性配置，本文以降低经济损失为目的改进了已有的配电网故障指示器最优配置目标函数。以一个小型农村10kV配电网络为例，阐述了配电网支路对工作人员寻找故障点平均时间的影响，从而简化了故障指示器配置的方案。在此基础上应用遗传算法对该10kV配电网的目标函数进行求解。Matlab计算结果表明：对于一个网架结构固定的配电网络，合理配置故障指示器有利于降低故障停电带来的经济损失；在故障指示器最优配置基础上增设故障指示器数目有利于降低寻找故障点的平均时间。

故障指示器；最优配置；遗传算法；配电网

农村 10kV配电网存在着网架结构较差、智能化程度低的缺点[1-2]。为了加快故障定位和缩短故障停电时间，帮助运行维修人员快速找到故障点，一些故障指示设备开始适用于配电网中，其中最常用的就是故障指示器。其工作原理为：在线路发生短路或接地故障后，故障线路从变电站出口到故障点支路的所有故障指示器因流过故障电流产生翻牌或闪光等醒目指示，而故障点后的故障指示器不动作。巡线人员沿着有故障指示器动作的主干或分支线路前行，则该主干或分支线路上最后一个翻牌的故障指示器和第一个没有翻牌的故障指示器区段，即为故障点所在区段，从而可迅速确定故障区段、分支及故障点。

国内对故障指示器的研究集中在故障算法判据原理[3-4]以及故障指示器研制上[5-6]，对于故障指示器配置数目与地点少有研究。目前，对于中长距离10kV架空线路配电网，配置故障指示器没有固定的方法，大多按照每隔一段距离便装设一个故障指示器，该方法不仅经济性差，对提升定位故障效果也不明显。本文对文献[7]提出的配电网故障指示器最优配置的目标函数进行改进，利用Matlab软件采用遗传算法对一个小型农村 10kV配电网进行故障指示器最优配置求解，从经济性角度对故障指示器最优配置方案进行选择，并在经济性最优配置的基础上探讨了故障指示器安装数量对寻找故障点平均时间及总费用的影响。

1 目标函数

从经济上考虑，目标函数可表示为

式中，CT为总费用；CBRK_i为区段i故障导致负荷中断造成的损失费用；CFI为线路安装故障指示器所需的费用。

目前，故障指示器主要使用GPRS跟主站通信和线路CT取电[8]，因此CFI费用主要由3部分构成，分别是故障指示器成本（FIprice），GPRS通信年费（FIgprs）及其网损（FIcost）。CFI可表示为

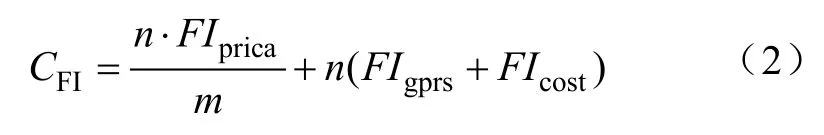
式中，n为安装故障指示器个数；m为故障指示器平均使用年限。

CBRK_i既包括本地区段负荷中断造成的损失，也包括因本地中断引起其他区段负荷中断造成的损失。CBRK_i可表示为

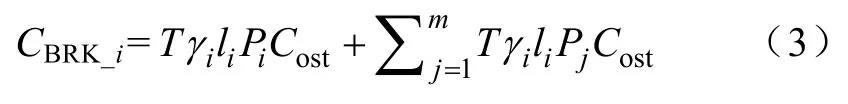
式中，Pi为i区段的负荷，单位kW；Cost为负荷点单位电量平均停电损失费用（¥/kW·h）的电价；li为i区段的线路长度，单位km；γi为i区段的故障概率（（次/km）/年）；T为故障中断时间。

在式（3）中，故障中断时间T由维修人员巡线时间Ti与故障修复时间Trep构成。其中Trep为固定值（不会对故障指示器最优配置产生影响，可忽略），Ti为变值，由式（5）计算。

式（5）中，V为维修人员巡线速度， Σli为巡线长度。文献[7]指出该区段有安装故障指示器时，巡线长度就是该区段长度。当该区段未安装故障指示器时，则巡线长度由上级区段最近安装故障指示器决定，其巡线距离为上级区段至故障区段，并加上该区段同一级未安装故障指示器区段，然而该计算方法默认已知故障区段，而实际中是无法预知具体哪个区段发生故障的。巡线长度应由故障线路下级第一个故障指示器不动作的区段和上级最后一个故障指示器动作的区段决定。如图1所示，假设D线路发生故障，线路仅仅G区段安装了故障指示器，根据故障指示器原理可知，G故障指示器不动作，由此可知G区段及其下级区段没有故障，故障区段在G区段前，工作人员无法预知故障发生在D区段，故最大巡线距离不是文献[8]所提到的LA+LB+LC，而是LA+LB+LC+LD+LE+LF。可以看出，当安装故障指示器过少时，其巡线长度较长导致故障修复时间长。

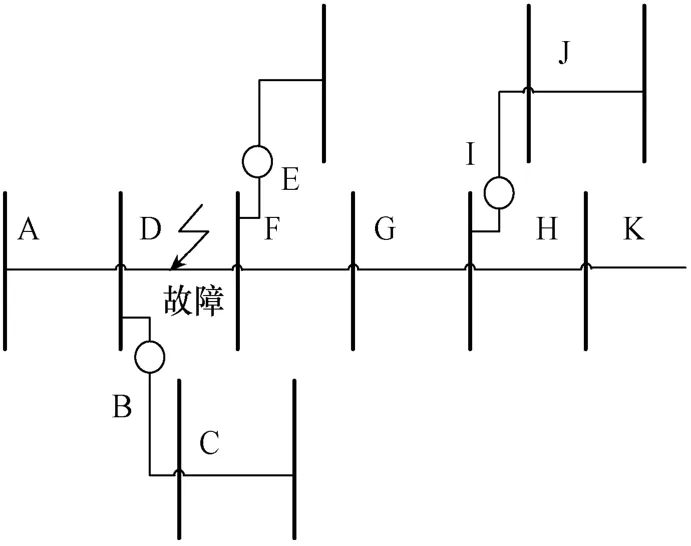
图1 故障线路示意图

为了进一步阐述Ti的求解过程，这里以TK为例进行说明。对于ADFGHK支路，其故障指示器的安设对巡线时间的影响为式（6）。式中，将有安装故障指示器的区段取值为1，否则取值为0。

对于ADFGIJ、ADE、ABC，其故障指示器安设对巡线时间的影响分别为式（7）、式（8）、式（9），即

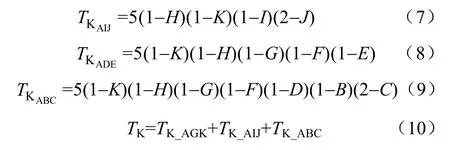
从TK式子中可以看出，故障指示器的数目对巡线时间产生很大的影响，特别是故障区段同一级与其前级支路未安装故障指示器的区段会造成额外的巡线时间，如。这对于复杂和支路多的配电网络影响更大。根据电网对供电可靠性的要求，可进一步简化故障指示器的配置方案，即配电网线路支路的首端必定要安装故障指示器。图1中的B、E、I区段必要安装故障指示器，从而消去了未安装故障指示器支路造成的额外巡线时间。

2 遗传算法

遗传算法（genetic algorithm，GA）是基于生物遗传及进化机制适用于复杂系统优化的自适应概率优化技术[9]。其本质是种高效、并行、全局搜索方法，使用生物界适者生存的原则，在潜在的解决方案中逐次产生一个近似的最优方案。

1）编码

对解空间的解数据进行编码，常用的有二进制数编码、整数编码以及树形结构编码[10]。本文采用二进制数编码，对于图2所示的一个小型配电网络，将区段B、E、I作为支路的首端，必须要配置故障指示器，故区段 ABCDEFGHIJK配置情况为“x1xx1xxx1xx”，当x值取1时，表示该区段安装故障指示器；当x值取0时，表示该区段未安装故障指示器。

图2 小型配电网络

2）初始种群生成

在可行解中随机生成一个8位种群，每一位代表每一个未知区段故障指示器配置情况。

3）适应度评价

适应度表示解的优劣性，本文目标函数可作为适应度函数。

4）选择、交叉、变异

选择是指父代种群中适应度高的个体，被选择的机会越多。交叉是指被选择的双亲以一定的交叉概率Pc确定是否交叉，确定交叉的双亲，随机选择交叉位置，彼此交换交叉位置之后或前的基因，产生新个体。变异一般是按位进行，以Pm概率改变某一位，生成新的个体[11]。

5）决定最优方案

在进化过程中所得到的具有最大适应度的个体一般为最优输出解，终止运算。

遗传算法流程如图3所示。

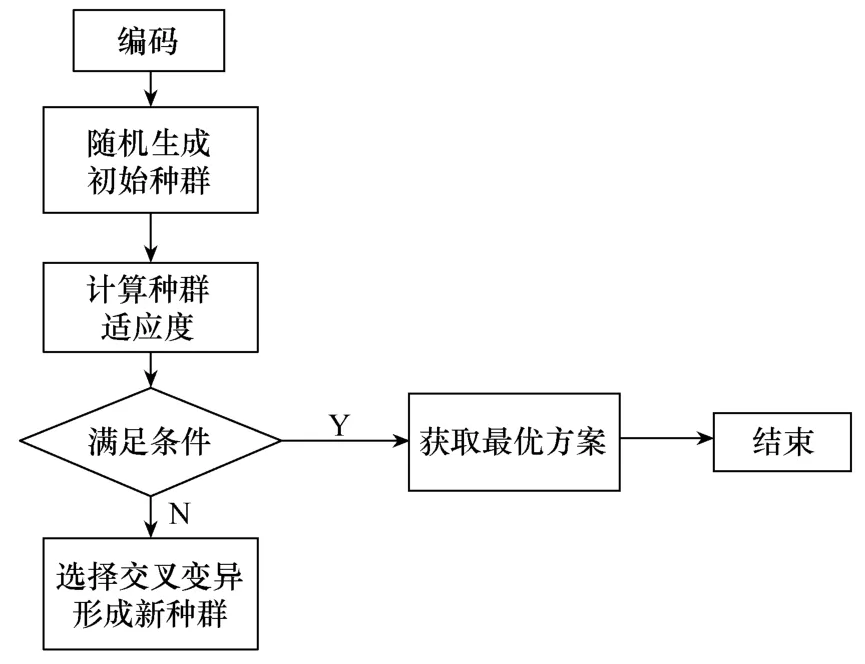
图3 遗传算法流程图

3 故障指示器最优配置

3.1 经济性最优配置方式

本文用Matlab对图2所示小型配电网进行算法测试，运算参数见表1[6]。

表1 算例线路参数

假定维修人员巡线速度为10km/h，故障指示器GPRS通信费用每年60元，网损200元每年，电费统一0.5元/kW·h。市面上一套故障指示器一般由太阳能电池板、可充电蓄电池、数据采集器、故障指示器以及上位机构成，假定一套故障指示器成本3000元。

测试中记录CT随迭代过程的变化，如图4所示。

由图4可见，最低总费用在10次左右迭代就趋于平稳，说明已寻找到故障指示器最低费用配置方案；总费用均值在25次左右迭代趋于平稳，说明此时被选出的故障指示器配置方案适应度高。35次迭代后的配置方案见表 2。表中 1表示线路安装故障指示器，0表示未安装。

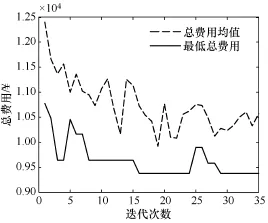
图4 总费用均值与最低总费用的变化

表2 最终8种最优配置方式

表3 不同配置方式的寻找故障点均时

从经济性的角度出发，由表3可以看出配置方式1、2、6为最佳配置方式，其全部费用是最低的。但寻找故障点平均时间为1.09h，相对较高。

3.2 安装数量对寻找故障点均时与总费用的影响

为了便于分析故障指示器安装数量对经济性的影响，本文取配置方式1为基本配置方式，在此基础上不断增加故障指示器的数目形成新的配置方式，见表4。

表4 故障指示器配置方式

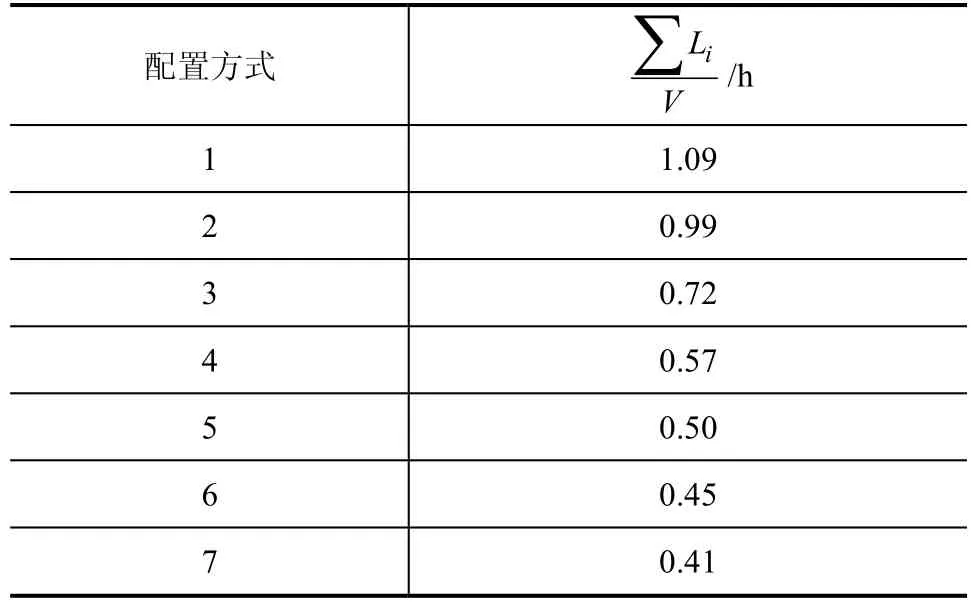
表5 不同配置方式的寻找故障点均时

图5 不同配置方式的寻找故障点均时与总费用的关系

由图5可以看出：

1）在经济性最优的故障指示器配置方式下不断增加故障指示器的配置数量，寻找故障点平均时间随之下降，但总费用随之增加。

2）对于不同区段线路增设故障指示器对降低寻找故障点平均时间效果不同。配置方式2、3、4增设的故障指示器区段分别为D、G、H，对降低寻找故障点平均时间效果明显，主要因为其处于网架结构的中间地段；配置方式5、6、7增设的故障指示器区段为K、C、J，对寻找故障点平均时间效果不明显，主要因为其处于网架结构的末端。

4 结论

寻找一个经济性最好并满足供电可靠性要求的故障指示器配置方式是一个极值优化问题。对于中长距离 10kV架空线路的故障指示器来说，最优配置方式主要受其网架结构及线路负荷量的大小影响。应用遗传算法优化故障指示器的配置，把所有可能区段的配置方式作为变量，从经济性角度找出满足要求的全局最优解。案例表明，对于一个固定网络的配电网，存在经济性最优的故障指示器配置方式。

从计算结果可以看出：经济性最优的故障指示器配置方式其寻找故障点平均用时相对较高，但对于农村用户来讲，可以接受。在经济条件允许的情况下，可在经济性最优配置的基础上适当增加大负荷区段或线路中间区段故障指示器的安装数量，这样有利于降低寻找故障点的平均时间。

[1]唐金锐,尹项根,张哲,等.配电网故障自动定位技术研究综述[J].电力自动化设备,2013,33(5)：7-13.

[2]姜健,鲍光海.小电流接地系统单相接地故障选线方法综述[J].电气技术,2015(12)：1-5.

[3]张丹洋,周浩.一种用于绝缘子闪络定位的新型无源故障指示器[J].电力系统保护与控制,2012,40(6)：119-124,141.

[4]童宁,余梦琪,林湘宁,等.基于相电流高频特征识别的配电网故障指示器原理[J].电工技术学报,2015,30(12)：465-471.

[5]李程.新型故障指示器的研制[D].北京：华北电力力学,2013.

[6]陈煦斌.新型配网故障指示器研究[D].北京：华北电力大学,2014.

[7]陈煦斌,秦立军.配网故障指示器最优配置研究[J].电力系统保护与控制,2014,42(3)：100-104.

[8]郭谋发.配电网自动化技术[M].北京：机械工业出版社,2012：111-112.

[9]王艳松,陈国明,张加胜,等.基于小生境遗传算法的配电网开关优化配置[J].电工技术学报,2006,21(5)：82-86.

[10]章文俊,程浩忠,王卫华.基于分布估计一单亲遗传算法的配电网规划[J].高电压技术,2009,35(6)：1476-1482.

[11]刘莉,宛力,陈学允.模糊遗传算法在配电网络综合优化中的应用[J].电力自动化设备,2001,21(1)：14-16.

Optimal Configuration of Fault Indicator in Intelligent Distribution Network

Jiang Jian Bao Guanghai
(College of Electrical Engineering and Automation Fuzhou University,Fuzhou 350116)

In order to realize the economic configuration of fault indicator.This paper improves the objective function of the optimal configuration principle of the existing distribution network fault indicator with the aim of reducing the economic loss.This papertake a small rural 10kV distribution network as an example,explainedthe influence of the branch of the power distribution network on the average time of finding the fault point,so the scheme of fault indicator configuration is simplified.On this basis,taking use of the genetic algorithm to solve the objective functionof the 10kV distribution network.The results show thatthe reasonable configuration of fault indicator is beneficial to reduce the economic losses caused by the failure of the fault.On the basis of the optimalconfiguration of the fault indicator,adding the number of fault indicator is good to reduce the average time to find the fault point.

fault indicator；optimal configuration；genetic algorithm；distribution network

姜 健（1991-），男，硕士研究生，研究方向为电气设备在线监测。