逐步分析法在解题教学中的实践

吴光亮

(江苏省泰兴市第一高级中学 225400)

逐步分析法是陕西师大罗增儒教授在关于中学数学教学多年研究中提出来的，其认为对于大部分中学生而言，数学知识的运用不可能一蹴而就，而是需要教师合理的引导、逐步的堆积，从合理的综合、整合中感受知识的整合，逐步分析成为将问题“庖丁解牛”的利器．

一、概念理解中的逐步分析

数学概念是数学学习的核心，逐步分析法在这一理解中体现了重要的作用．我们知道，概念的认知有一个逐步加强、螺旋式上升的过程，通过不断的理解认识，才能对概念的认识有更深的理解．例如：奇偶函数定义对学生来说，是一个逐步分析的提高过程，这一概念的理解不是一步到位的．我们来看教师在奇偶函数概念理解中的设计：

问题组1 ①f(x)=2x2+1,x∈R；

②f(x)=2x2+1,x∈[-2，2]；

③f(x)=2x2+1,x∈[-2,2)；

④f(x)=2x2+1,x∈(0,+∞).

分析 对于单一解析式的基本初等函数判断其奇偶性，学生掌握和理解都是基本到位的，其主要通过代数判断方式或者是图形判断，第一层次的概念分析基本到位，学生的理解也是到位的．

问题组2 ①f(x)=0,x∈[-6,-2]∪[2,6]；

②f(x)=|x-2|+|x+2|；

③f(x)=|x-2|-|x+2|；

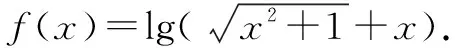
通过概念教学案例，我们发现要提高概念的理解，结合案例的逐步分析必不可少，这种分析既提高了学生对于概念的理解力，也提升了学生对于概念的逐步认识，因此逐步理解、逐步分析，对于大部分学生而言是有效和合适的．

二、知识运用中的逐步分析

如果说概念是数学教学的核心，那么数学知识的运用则是数学教学的重要组成．近年来愈来愈多的试题侧重考查的是知识的综合运用能力，从这些问题的分析中，更要体现教师是如何逐步分析、庖丁解牛，将整合性的数学问题一步一步地展示出来，引导学生理解知识是如何运用的．

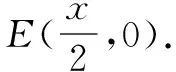
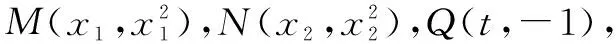
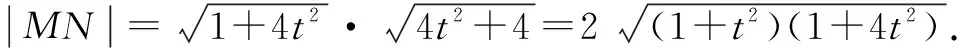
本题从知识综合运用的角度出发，将各种综合性的知识运用到一个问题中，获得了知识整合的运用能力．其实不难发现，解析几何最值问题往往是函数模型的探索，常规的直线和圆锥曲线位置关系的运算是根本保障，导数对于切线或判别式法的运用也是常态．

逐步分析法将概念教学、知识运用等等，都以一步一步分析的方式展示出来，以求学生能从基本——运用——理解——内化这一步骤不断上升，加强知识的理解和使用，成为数学学习更为有效的一种手段．

[1]石志群.高考数学命题思路分析及复习策略[J].中学数学月刊,2009(11).

[2]渠东剑.探究方法比探究结果更重要[J].中学数学教学参考(高中),2013(4).

[3]宋卫东.从生“动”到生动,诠释思维品质的提升[J].中学数学月考,2013(5).