如何高效的进行高中数学复习

刘 鼎

(华中师范大学第一附属中学 430000)

进行高中数学复习，既要注重基础知识的复习，更要注重数学解题能力的突破，要以解题思维训练为主，这样才能收到较好的复习效益.笔者结合自己的情况，谈几点复习体会，以期对复习备考的同学们提供参考.

一、打牢基础，熟悉数学解题思路程序

要提高数学的复习效果，首先，必须要打牢数学基础知识，在复习中要强化对数学基础知识的掌握，只有把基础知识掌握牢固，才能奠定解题的基础；其次，注重解题思路的训练.进行数学解题需要掌握正确的解题思路：一是审题.通过认真阅读题目，确定已知条件和需要求的求知量，然后再将题目的文字 语言转化成数学符号语言，并找到隐含条件，建立数学模型，初步确定解题思路；二是分析.分析题目所给条件与结论的关系，要考虑通过已知条件来求未知量还需要哪些条件以及如何求出这些条件，找出正确可行的解题思路.三是解题.根据形成的解题思路进行解题，并求出结果来检验解题思路的正确性.四是反思.主要是对所求答案进行检验，检验答案是否与已知条件有矛盾，从而确定正确答案.

例1 求函数y=log2(x2-2x-3)的单调增区间.

解题分析 多数同学的解题思路如下：令u=x2-2x-3=(x-1)2-4.又y=log2u为增函数，并且u在(1，+∞)上单调递增，再按照复合函数“同增异减”的性质，可求出函数的单调递增区间是(1，+∞).

点评 虽然多数同学掌握复合函数增减性的解题方法，并且判断思路也正确，但是在分析问题时不够严谨、全面，只考虑了“同增异减”这个性质，却没有对函数定义域分析，扩大了定义域取值范围，导致解题错误.

二、优化策略，掌握多种解题思想方法

在高中数学复习中，掌握灵活多变的解题思想方法是提高解题效率的关键，好的方法能够起到事半功倍的解题效率.在复习中应该注重优化解题的方法策略，注重在解题中选择科学恰当的数学思想方法.历年来高考数学试题也非常重视对数学思想方法的考查.因此，不应过度地去研究那些偏、难、怪题的特殊解法，而应把重点放在常用的解题方法的掌握上，并在解题中做到灵活运用.

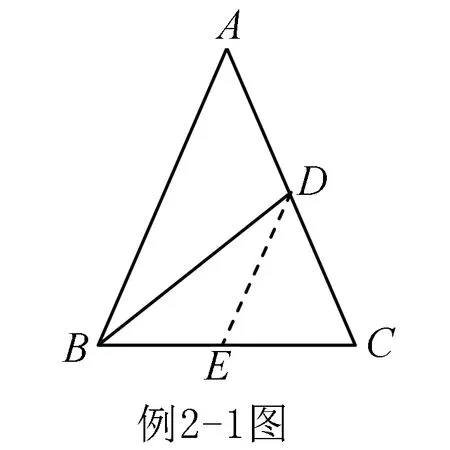
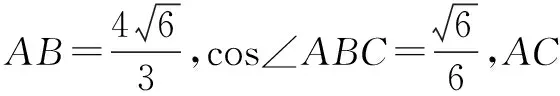
解题分析 对于此题可以灵活运用多种方法进行解答，以提高解题的效率.

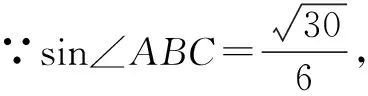
三、融会贯通，加强综合解题能力训练

在打牢基础，掌握多种解题方法的基础上，把各部分知识和解题方法做到融会贯通是很重要的.这就要注重加强综合解题能力的训练，来开阔解题思路，对提高解答综合类习题会有很大帮助，也能在高考中提高综合题目的解题效率.

例4 有等差数列{an},其前n项之和是Sn,a3=12,S12>0,S13<0.(1)求公差d的取值范围；(2)求S1,S2,S3,…,S12中的最大值，并讲出原因.

解题分析 (1)在本题中利用方程(不等式)的思想就比较容易求解问题，通过利用通项公式an和前n项和公式Sn来构建不等式就能方便求出公差的范围.(2)对于在数列问题中求前n项和的最大值问题，利用函数的思想和方法，把Sn的表达式转化成二次函数，这样问题就变成求函数最值问题，此题就容易解决了.此题在解答中用到了方程、不等式、函数等知识和方法求解，这样既能把各种知识融会贯通，又能提高解题效率.

总之，在高中数学复习中，就要抓住数学学习的核心和关键问题来复习，要把数学思想方法和解题的思路作为复习和训练的重点，这样既能有效提高复习质量，又能提高复习的效率和有效性.

[1]周亚.高效的高三数学复习法[J].科学咨询,2010(12).

[2]胡少吴.如何进行高三数学总复习[J].福建教育学院学报,2002(06).