基于场图的磁共振扩散张量成像变形矫正和信号补偿
康泰山,杨天和*,林建忠,张家兴
近年来随着高场磁共振检查仪的广泛普及,弥散张量成像(diffusion-tensor imaging,DTI)技术观察颅脑白质神经传导束走行的独特优势已广泛应用于临床且越来越受到重视[1-2]。DTI是一种对组织微环境改变十分敏感的成像技术,随着磁场越来越强,DTI成像中因磁敏感伪影引起的图像空间变形及体素信号丢失也越严重,从而导致DTI在与3D-T1像融合过程中出现白质区域错位,限制了DTI的临床应用[3]。DTI序列因相对较长的回波读出时间,故其对磁场的不均匀性敏感。局部磁场的不均匀性会导致空间变形及体素信号丢失,主要发生在颞叶和前额叶等脑组织与空气和骨骼的交界面。这种变形及信号丢失在频率编码方向上很小,因此主要是相位编码方向需要进行变形矫正[4]。本研究基于场图(field map)方法对高场DTI图像进行相位反卷积变形矫正及信号补偿[5-6],探索场图方法对DTI图像变形及信号丢失的矫正和补偿效果。
1 材料与方法
1.1 一般资料
收集2015年5月至2015年9月在我院磁共振科因神经系统症状而接受头颅磁共振检查,但未发现器质性病变者29例,其中男17例,女12例,年龄20~35岁,平均(26±5.3)岁。所用数据都告知研究对象,研究对象签署知情同意并接受追加脑功能扫描。
1.2 磁共振扫描序列
磁共振成像仪为德国Siemens公司生产的3.0 T Verio型医用磁共振成像系统,8通道高分辨率头颅线圈。静卧扫描,扫描时以现场确认数据的完整性及可用性后结束扫描。扫描序列如下:(1)GRE-field-mapping序列参数:轴状位扫描,激励次数1次,FOV=230 mm×230 mm,TR=488 ms,TE1/TE2=4.92 ms/7.38 ms,ΔTE=2.46 ms,采样矩阵=128×128,层厚=3 mm,间隔=0 mm (采用隔层扫描技术),相位编码方向A>>P。(2) DTI序列扫描参数:TR=10 s,TE=95 ms,b值为1000 s/mm²,弥散施加方向数30,回波间隙为0.95 ms,FOV、采样矩阵、层厚、间隔及空间定位均与GRE-field-mapping序列一致。(3) 3D-T1-MPRAG-sag序列参数:TR=1900 ms,TE=27 ms,TI=900 ms,采样体素为1 mm×1 mm×1 mm。(4)常规序列:轴状位T1-TSE,轴状位T2-TSE,矢状位T2-TSE,冠状位T2-FLAIR。
1.3 变形矫正及信号补偿
采用国际上公开发布的FSL软件包(FMRIB Software Library)5.0及Freesurfer 6.0软件包(surfer.nmr.mgh.harvard.edu)对数据进行处理。分析步骤如下:
(1)头颅运动校准:DTI及场图序列扫描时患者头颅的轻微晃动行自身运动校准,保证DTI和场图影像数据空间位置上的一致性。
(2)对DTI图像的相位卷积变形进行反卷积处理。场图矫正方法应至少采集2个不同回波时间图像并计算在相位上的变化,通过线性插值计算变形图像的每段线性函数在无变形图像中的空间位置,然后应用无变形体素位移图作为模版对变形图像进行矫正,从而建立无变形图像。场图矫正方法主要有以下4个步骤[7]:
从相位场图中计算相位的变化:
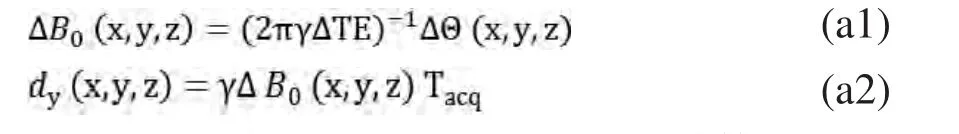
假定y为相位方向,通过线性内插计算出变形矫正后的图像:

在相位编码方向上信号值的矫正补偿:
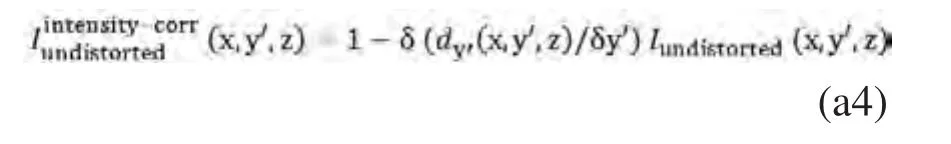
(x,y,z)代表图像中的体素坐标,ΔB0(x,y,z)代表B0场的非均一性差异值,单位是Hz。ΔΘ(x,y,z)代表体素在时间ΔTE中的不同相位测量值,γ代表旋磁比,dy代表场图中的体素在Y轴方向上的平移。Tacq代表一层原始数据的读出时间。
(3)信号补偿:针对因变形导致的信号丢失及B1场不均匀而导致信号采集时的不均匀,采用基于目标函数(cost-function)掩模法进行补偿修复[8-9]。为了实现信号补偿,必须通过最优化如下目标函数:
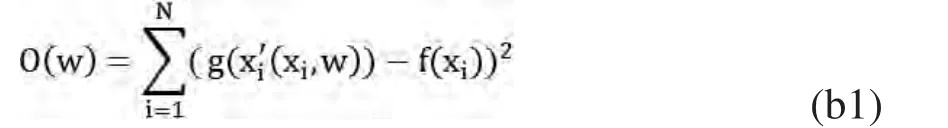
上式中f代表参考图,g代表需要进行信号补偿的图像。虽然要求解上述目标函数意味着参考图与重建图像之间必须非常相似,然而它也在进行优化求解的时候拥有明显的优点。
上述问题是一个典型的非线性最优化问题,需要寻找合适的w来最小化O。有多种不同的最优化方法可以求解上述方程。这些方法各有优缺点,笔者这里选择高斯-牛顿法进行最优化求解。该方法提供了一个直接的公式用于计算参数w:
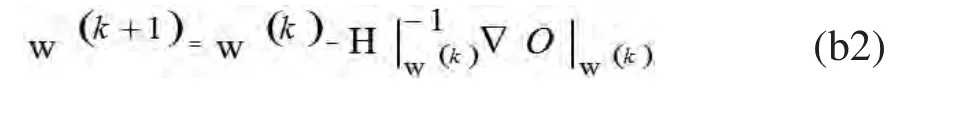
(4)对DTI图像进行涡流校正并最终计算张量结果。
(5)采用线性[自由度(dof)=12]脑沟边缘配准到3D-T1-MPRAG-sag结构像并融合。
1.4 变形矫正观察
将变形矫正前/后计算出的各向异性分数(fractional anisotropy,FA)值图与3D-T1-MPRAG-sag结构像进行线性配准(dof=12),使其空间位置基本一致,然后以FA大于0.2为阈值,勾画出FA值图白质边缘并与结构像白质边缘融合。应用脑功能软件Freeview (surfer. nmr. mgh. harvard. edu)对图像进行融合显示。将变形矫正前计算出的FA值图与经过场图变形矫正及信号补偿后的FA图线性配准到3D-T1-MPRAG-sag图像进行融合对比,观察白质FA值图边缘与结构像白质边缘对齐情况。
1.5 信噪比测量
根据场图改变较大的双侧额叶底部及中颅窝底部(颞叶)选择感兴趣区域(region of interest,ROI)(图1所示蓝色圆形区域)。另选择对磁场不敏感丘脑区域(图1所示的红色圆形)作为参照。信噪比(signal to noise ratio,SNR)计算公式为SNR=S/N。处理前后信噪比改变量的计算公式如下[10]:(纠正后信噪比-纠正前信噪比)/纠正后信噪比×100%。双侧额叶和颞叶对照丘脑中心的信噪比计算公式如下:(纠正后信噪比-纠正后丘脑中心信噪比)/纠正后丘脑中心信噪比×100%。
1.6 FA值测量及计算
选择信号丢失明显区域,由两位高年资诊断医师确认前后位置一致性,计算其前后FA值。计算公式如下:(纠正后FA-纠正前FA)/处理后FA×100%。
1.7 统计学处理
应用SPSS 19.0软件进行数据处理及统计分析。纠正前、后相同部位ROI测量值比较采用配对t检验,P<0.05为差异有统计学意义。
2 结果
经过场图矫正处理后:(1)信号的丢失得到补偿:额叶和颞叶底部信号经变形纠正及场不均匀补偿后增益达15.8%~16.2% (表1)。(2)FA值信号的丢失得到恢复:额叶和颞叶底部FA值经变形纠正及场不均匀补偿后增益达17.5%~18.3% (表1)。(3)空间变形得到明显矫正:经过Freeview软件对比显示,额叶和颞叶的白质在空间位置上对位整齐,与3D结构像能很好地匹配融合(图2)。(4)场图矫正处理不改变未变形的脑组织信号:丘脑中心因位于大脑中心部位受磁敏感伪影影响极小,纠正前后信号经变形纠正后增益仅为1.5%左右,FA值增益仅为1.02%~2.12% (表1)。额叶和颞叶底部纠正后的信号与丘脑中心的信号无明显差异,二者的百分比在1.9%以内(表2)。
3 讨论
DTI是一种磁共振功能成像,它能无创地显示脑内神经纤维束的走行、脑功能区间白质纤维束的连接及提示脑内神经结构是否异常。目前DTI在脑白质评价和神经外科手术导航计划设定等方面显示了独特优势[11-12]。DTI需要应用平面回波成像(echo planar imaging,EPI),但是EPI在磁化率差异大的组织边界会产生严重的几何变形,特别在颅底前额叶和颞叶更为明显,这种变形随场强增高更加明显。空间几何的变形、体素位移及信号的丢失都会影响DTI与结构像的配准,并最终影响结果的准确性。因此,对DTI进行去伪影研究具有重要的实际意义[13]。
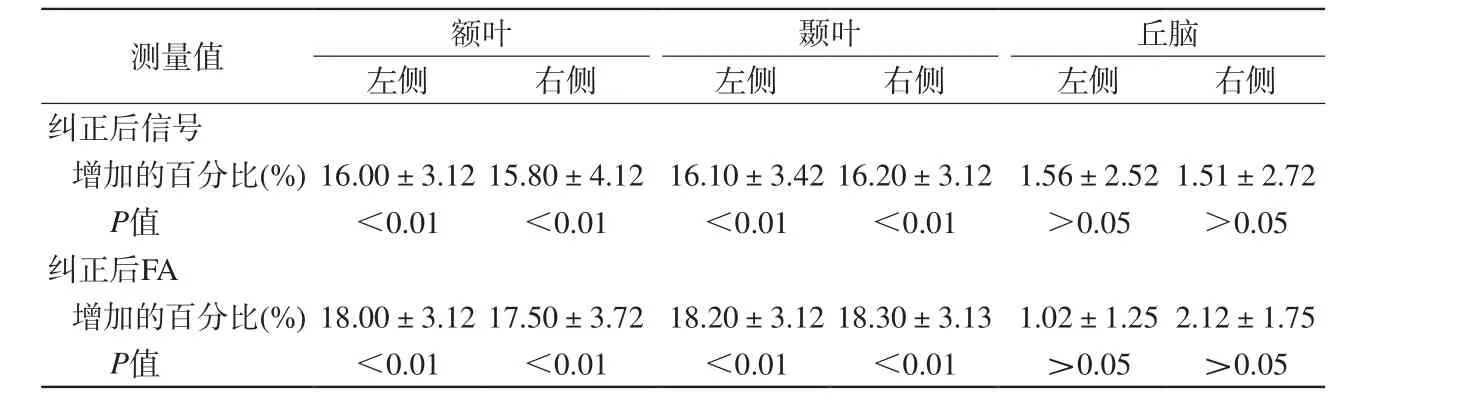
表1 各观察脑区测量值纠正后增加的百分比Tab. 1 Percentage of the increase of each measure in the observed brain regions after rectification or compensation
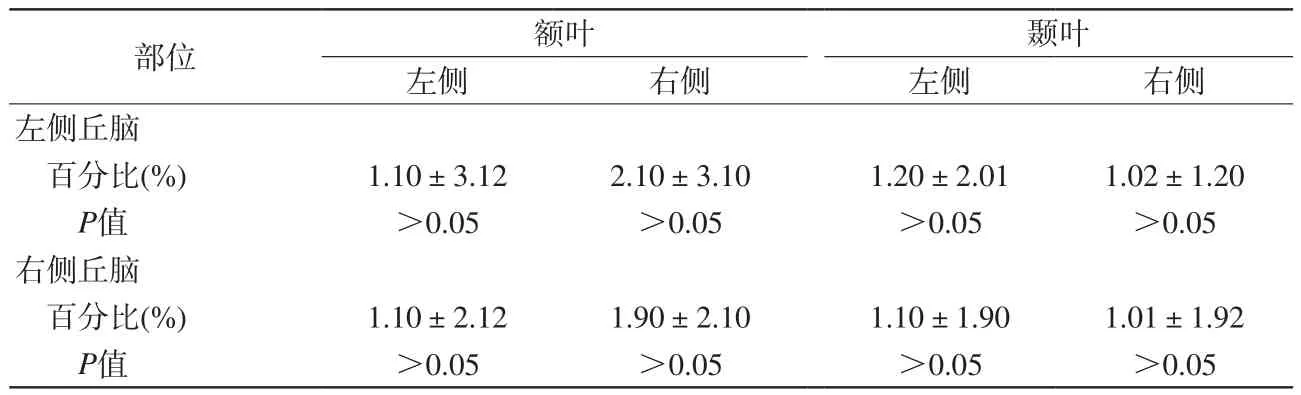
表2 额叶和颞叶补偿后信号分别与同侧丘脑纠正后信号差异的百分比Tab. 2 Percentage of the compensated signals in the frontal and temporal lobes compared to that in the collateral thalamus, respectively
克服DTI的畸变主要通过成像序列的优化,如早期的分段EPI序列联合导航回波扫描技术和线阵扫描弥散成像技术等。但这些方法均各有优缺点,它们至今尚不能很好地应用于临床[14]。近年来,国内一些学者对DTI数据进行了分析前处理。例如王毅等[15]提出了一种基于图割的DTI分割算法来精确分割胼胝体;何晓璇[16]针对DTI图像的磁敏感伪影,通过涡流校正来减小相应的图像畸变,并采用基于边界约束的代价函数来保证DTI图像的配准精度。本研究采用场图矫正方法对传统平面回波DTI序列图像进行基于体素的相位反卷,磁场不均匀导致的变形得以矫正,使以结构像为解剖定位的局部FA和MD等值测量更加准确。同时,本研究变形纠正的结果使得DTI与结构像能够很好地匹配,也使得以结构像的解剖位置定位进行的纤维示踪能够与功能像融合更精确。
本研究对体素位移进行回复及采用目标函数掩模法对信号丢失进行补偿,信号易丢失区域(额叶和颞叶)信号显著提高了15.8%~16.2%,但场影响最小区域(丘脑)信号却无显著提高(1.51%~1.56%),因此该信号补偿方法可以减少因场不均匀造成的信号丢失,使结果接近实际状况。原始图像信号丢失及变形同时影响最终结果变化。本研究显示FA值在信号补偿后也增加了17.5%~18.3%。因此,本研究基于体素场图对DTI的变形矫正及信号丢失的补偿取得了显著的效果。本研究中基于场图方法对高场DTI图像进行的相位反卷积变形矫正及信号补偿是一种独立的图像后处理技术,适用于西门子、GE和飞利浦MRI机型的脑数据前处理。
本研究还存在以下两点不足:(1)大幅度头动造成的明显位移没有得到较好矫正;(2)图像数据的校准需从主机导出并应用第三方软件逐步计算,步骤较复杂,有待新序列的进一步研发。总之,本研究表明基于场图方法对DTI图像的变形矫正,使空间变形得到显著的改善,磁敏感区域信号的丢失得到补偿。
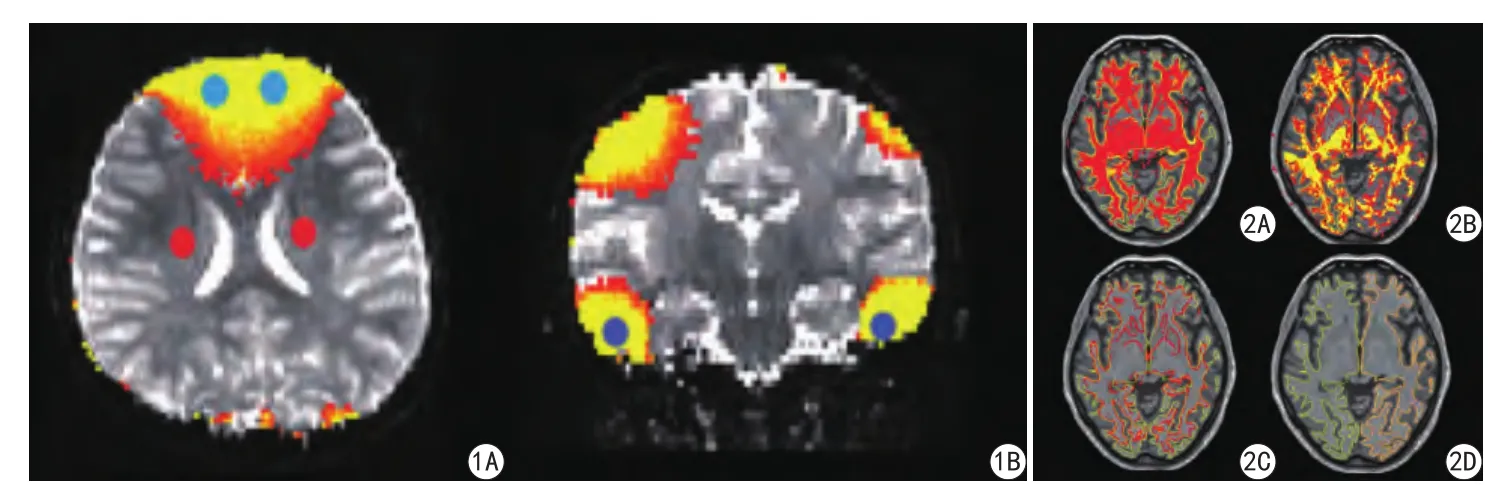
图1 脑区信噪比测量选择示意图。蓝色圆形为双侧额叶和颞叶选择感兴趣区域(A、B)和红色圆形为对照丘脑区域(A) 图2 A:纠正前FA图(阈值>0.2),为mask与3D结构像融合图(dof=12)。白质区域的对齐出现错位。B:纠正后FA图(阈值>0.2),为mask与3D结构像融合图。白质区域对位整齐。C:将图A分别用线条勾画出来显示。黄色线勾画的是3D结构像灰、白质交界,红色线勾画的是FA图的脑白质边界。D:将图B分别用线条勾画出来显示。黄色线勾画的是3D结构像灰、白质交界,红色线勾画的是FA图的脑白质边界Fig. 1 Sketch map of brain regions selected for signal to noise ratio measure. Blue circles located in the bilateral frontal and temporal lobes (A, B), while red circles located in the bilateral thalamus (A). Fig. 2 A: FA map before rectification (threshold >0.2), It is a fusion map of mask with 3D image (dof=12). It shows white matter matched error. B: FA map after rectification (threshold >0.2), It is a fusion map of mask with 3D image (dof=12). It shows white matter matched well. C: The outline of FA map showing match error in (A). Yellow line shows the border of gray matter and white matter in 3D structural image and red line shows the border of white matter in FA map. D:The outline of FA map showing match well in (B). Yellow line shows the border of gray matter and white matter in 3D structural image and red line shows the border of white matter in FA map.
[References]
[1] Shahar T, Rozovski U, Marko NF, et al. Preoperative imaging to predict intraoperative changes in tumor-to-corticospinal tract distance: an analysis of 45 cases using high-field intraoperative magnetic resonance imaging. Neurosurgery, 2014, 75(1): 23-30.
[2] Kockro RA, Reisch R, Serra L, et al. Image-guided neurosurgery with 3-dimensional multimodal imaging data on a stereoscopic monitor. Neurosurgery, 2013, 72(Suppl 1): 78-88.
[3] Yin JZ. Common artifacts in 3.0 T high-field MRI systems: principle,appearance and remedy. Chin J Magn Reson Imaging, 2010, 1(4):291-294.尹建忠. 3.0 T高场磁共振设备的常见伪影: 原理、表现与对策. 磁共振成像, 2010, 1(4): 291-294.
[4] Irfanoglu MO, Walker L, Sarlls J, et al. Effects of image distortions originating from susceptibility variations and concomitant fields on diffusion MRI tractography results. Neuroimage, 2012, 61(1):275-288.
[5] Robson MD, Gore JC, Constable RT. Measurement of the point spread function in MRI using constant time imaging. Magn Reson Med, 1997, 38(5): 733-740.
[6] Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magn Reson Med, 1995,34(1): 65-73.
[7] Hutton C, Bork A, Josephs O, et al. Image distortion correction in fMRI: A quantitative evaluation. Neuroimage, 2002, 16(1): 217-240.
[8] Rorden C, Bonilha L, Fridriksson J, et al. Age-specific CT and MRI templates for spatial normalization. Neuroimage, 2012, 61(4):957-965.
[9] Huang Q, Zhang R, Hu X, et al. Disturbed small-world networks and neurocognitive function in frontal lobe low-grade glioma patients.PloS One, 2014, 9(4): 94095.
[10] Huang YT, He CM. Evaluation methodology of MRI SNR. Chin J Magn Reson Imaging, 2012, 3(2): 149-152.黄艳图, 何超明. 磁共振成像信噪比的评价方法. 磁共振成像,2012, 3(2): 149-152.
[11] Jones DK, Leemans A. Diffusion tensor imaging. Methods Mol Biol,2011, 711(711): 127.
[12] Han T, Cui SM, Tong XG, et al. Three-dimensional visualization of functional brain tissue and functional magnetic resonance imagingintegrated neuronavigation in the resection of brain tumor adjacent to motor cortex. Int J Med Radiol, 2011, 34(3): 205-210.韩彤, 崔世民, 佟小光, 等. 大脑功能组织可视化及fMRI术中导航在脑肿瘤切除术中的应用. 国际医学放射学杂志, 2011, 34(3): 205-210.
[13] Gupta A, Escolar M, Dietrich C, et al. 3D Tensor normalization for improved accuracy in DTI tensor registration methods//biomedical image registration. Berlin: Springer Berlin Heidelberg, 2012:170-179.
[14] Wang HY, Zhao B, Yu FH, et al. The principle of diffusion tensor imaging techniques and comparison. J Med Imaging, 2006, 16(4):402-404.王海燕, 赵斌, 于富华, 等. DTI常用扫描序列原理及比较. 医学影像学杂志, 2006, 16(4): 402-404.
[15] Wang Y, Xie K, Zhou YJ, et al. Graph cut based algorithm for corpus callosum segmentation from diffusion tensor images. J Beijing Polytechnic University, 2014, 40(3): 473-480.王毅, 谢琨, 周艳娟, 等. 基于图割的扩散张量磁共振图像胼胝体分割算法. 北京工业大学学报, 2014, 40(3): 473-480.
[16] He XX. Imaging study of focal cortical dysplasia based on magnetic resonance imaging. Hefei: University of Science and Technology of China, 2016.何晓璇. 基于磁共振结构像的局灶性皮质发育不良的影像学研究.合肥: 中国科学技术大学, 2016.

