基于顶帽变换和LBP算子的纹理特征提取方法
王升峰+杨永全

摘 要:针对顶帽变换能有效消除不均匀背景这一特点,结合LBP算子能很好地描述图像局部空间结构以及在纹理分类中有高区分能力的特点,提出了顶帽变换和LBP算子相结合的多特征组合纹理特征提取方法。经实验验证可知,这种多特征组合的纹理特征提取方法能够提高对Outex数据集分类的准确率,并得出结论:特征提取方法应当遵循多特征组合、组合特征间差异大和组合特征维数小的原则。
关键词:顶帽变换;LBP;多特征组合;纹理特征提取
DOIDOI:10.11907/rjdk.162266
中图分类号:TP301
文献标识码:A文章编号:1672-7800(2016)012-0005-03
0 引言
纹理是人们描述和区分不同物体的重要特征之一,它作为物体表面的一种基本属性广泛存在于自然界中,是人们视觉系统对自然界物体表面现象的一种感知,是图像中普遍存在而又难以描述的特征,虽然人们对纹理的研究已有几十年的历史,但至今难以对纹理给出统一、准确的定义[1-5]。
20世纪70年代以前出现了自相关函数法,功率谱方法和一些与各种灰度频率相关的方法等[6-8]。这些方法取得了一定成功,但是没有具体的定义、描述或纹理模型,仅仅是某种数学变换。另外还有一些提取纹理特征的方法[9-10],也仅限于提取特定的图像属性,如纹理粗糙度、纹理直线性等。自20世纪80年代以来,MRF理论在纹理分析中掀起一阵热潮[11],为纹理特征提取找到了一个新的方向,90年代以后,人们发现传统的纹理分析方法的一个瓶颈在于不能从多尺度有效描述纹理特征。小波理论[12-13]的出现为时频多尺度分析提供了一个更为精确而统一的框架。近年来,较引人瞩目的是Ojala[14]等于2002年提出的局部二进制模式(LBP)[15-17],该方法分析纹理的吸引人的地方在于其计算复杂度小,具有多尺度特性和旋转不变特性,在纹理检索领域得到应用。在前人总结的基础上,再结合顶帽变换[18]能有效消除不均匀背景这一特点,本文提出了顶帽变换和LBP算子相结合的多特征组合纹理特征提取方法。
1 顶帽变换
帽变换技术作为灰度形态学的重要应用之一,是一种非均匀背景问题的解决方案。
图像f的顶帽变换h定义为图像f与图像f的灰度开运算之差,可表示为:
h=f-f(f°b)(1)
2 局部二值模式(LBP)
局部二值模式(Local Binary Pattern,LBP)算子是一个描述图像局部空间结构的非参数模型算子,LBP算法思想简单容易理解、计算复杂度小、对单调的灰度变换不敏感并且能够很好地描述图像的局部纹理特征[19]。最早出现的是基本的LBP,在原始的LBP算子提出后,研究人员不断提出了各种改进和优化,又相继出现了圆形领域的LBP(LBPP,R)、均匀LBP(LBPu2P,R)、完整LBP等。
3 纹理特征提取
首先给出一些符号定义:符号TR表示以半径为R的结构元素对原图像进行顶帽变换处理,如T10表示以半径为10像素的结构元素对原图像进行顶帽变换处理,T5则表示以半径为5像素的结构元素对原图像进行顶帽变换处理;符号TR-LBPp,R1表示对以半径为R的结构元素进行顶帽变换处理的结果图像进行LBPP,R1纹理特征描述;符号T2R表示对TR进行二值化处理,即原图像经TR处理后再进行二值化处理的结果图像;符号T2R-LBPP,R1表示对T2R处理后的结果图像进行LBPP,R1纹理特征描述。
图1中(a)图像为原图像,(b)图像为原图像的LBP8,2纹理特征描述;
图2中采用半径为10的圆形结构元素对原图像进行顶帽变换处理,如(a)所示,(b)为(a)的LBP8,2纹理特征描述,(c)为图像(a)的二值化处理结果,(d)为(c)的LBP8,2纹理特征描述,即原图像的T210-LBP8,2纹理特征描述;图3中所包含图像与图2保持一致,只是采用了半径为5的圆形结构元素对原图像进行顶帽变换处理。对比图2与图3中(d)图像,可以看出T210-LBP8,2通过调节结构元素的半径,对原图像进行顶帽变换处理后能够得到不同粒度的原图像细节信息。
在前人研究的基础上,本文提出如下多特征组合的纹理特征提取方法:采用对原图像的LBPP,R1纹理特征描述和原图像的LR-LBPP,R1纹理特征描述进行组合作为最终的纹理特征提取,用符号LBPP,R1-LR-LBPP,R1表示。这种多特征组合的纹理特征提取方法的更一般符号表示为:LBP-T2RLBP。
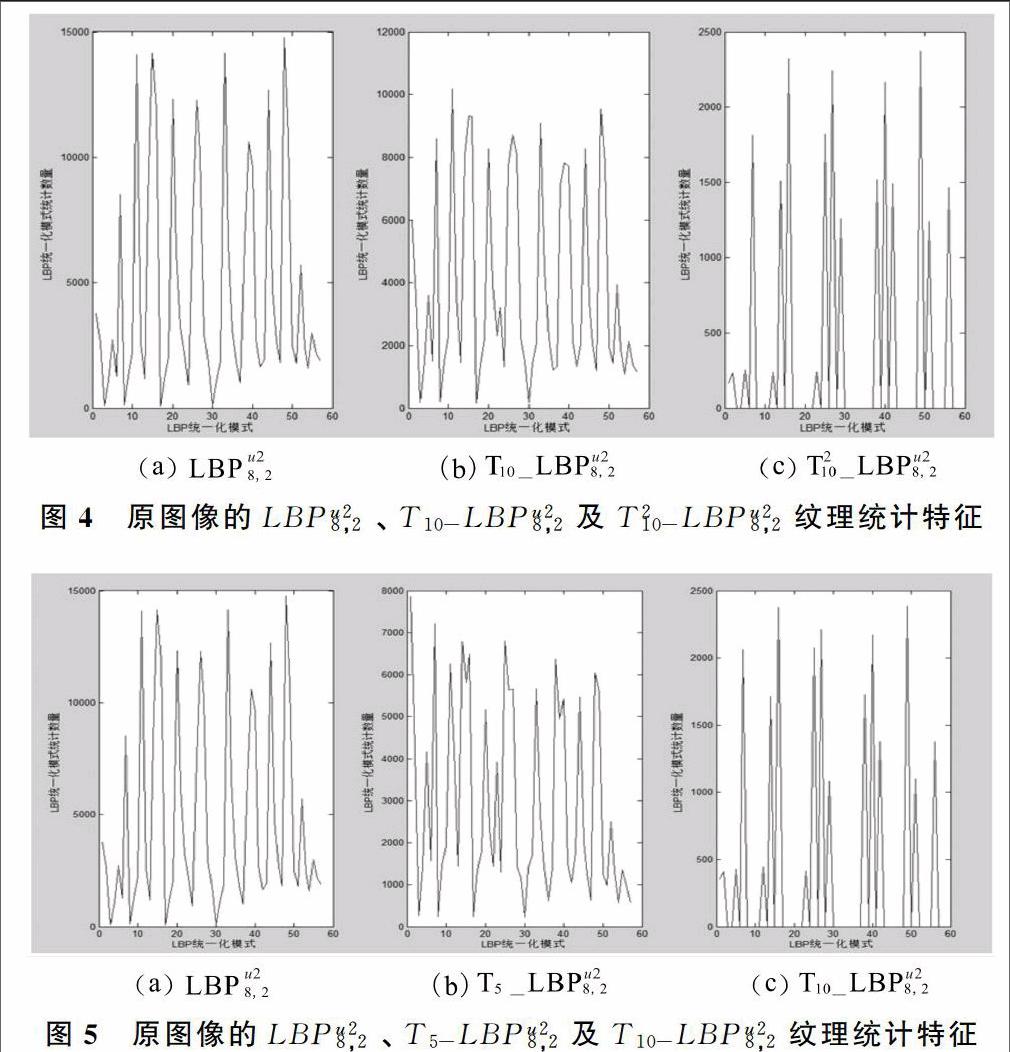
上述内容中给出了LBP-T2RLBP纹理特征提取方法,但并未解释该纹理特征提取方法为什么选择上述两种特征进行组合而不选择其它特征的组合(如LBP-TR-LBP或TR-LBP-T2R-LBP),下文将给出详细分析。为了方便对比分析,先给出原图像的LBPu28,2、T10-LBPu28,2及T210-LBPu28,2纹理统计特征图和原图像的LBPu28,2、T5-LBPu28,2及T10-LBPu28,2纹理统计特征图,如图4和图5所示。
对比图4中的(a)和(b)或图5中的(a)和(b),可以看出:除几个细小的变化不同外,(a)图和(b)图的统计变化曲线大致保持一致。这说明(a)图和(b)图所描述的特征非常相似,如果对这两个特征向量进行归一化处理,它们之间的距离会非常小。因此(a)图和(b)图所描述的特征组合作为特征提取会存在特征信息冗余。在实验过程中采用(a)图和(b)图所描述的特征组合作为特征提取与仅采用(a)图所描述的特征作为特征提取所取得的分类准确率几乎没有差异,这也证明了上述分析的正确性。 (a)图和(b)图的相似也正好说明了LBP算子能有效地消除光照影响,因为(b)图是原图像经过顶帽变换后得到的统一化LBP统计特征,顶帽变换有效地消除了不均匀背景,而不均匀背景往往是由光照引起的。至于为什么不选择组合图4中的(b)和(c)或图5中的(b)和(c),而选择(a)和(c)的组合,先要对(c)图进行分析。
根据顶帽变换消除不均匀背景的效果——原图像经过顶帽变换后得到的图像分量能够更加合理地描述原图像中实物的细节信息。采用相同的方法分别对原图像和原图像经过顶帽变换后得到的图像进行二值化,原图像经过顶帽变换后得到的图像在经过二值化后具有更多的细节信息,这表明经过顶帽变换后得到的图像分量的灰度分布能更合理地描述出原图像中实物的细节部分,因此顶帽变换能够有效地帮助获得图像中的细节信息,这些细节信息往往就是具有较强区分力的信息,获得这些细节信息也就是形态学图像处理的本质——抓住目标对象最为本质(最具区分能力—Most Discriminative)的形状特征。(c)图对这些细节形状特征进行了统计描述。
再对图2或图3中的(c)图进行观察,可以看出,其(c)中几乎没有包含背景信息,这也是为什么选择组合图4中的(a)和(c)或图5中的(a)和(c),因为通过其(c)可以抑制(a)中所包含的背景信息产生的对特征区分能力的干扰(背景往往是不太被关注的信息)。那么为什么不选择组合图4中的(b)和(c)或图5中的(b)和(c),原因在于顶帽变换的本质实际上相当于滤波处理,它过滤掉了原图像中实物的一些轮廓信息,而轮廓信息往往具有较强的区分能力。因此提出了LBP-T2RLBP纹理特征提取方法。对于顶帽变换会增强噪声以及LBP对噪声较为敏感的缺点,可以采用MB-LBP算子来处理。
4 实验结果分析及性能评价
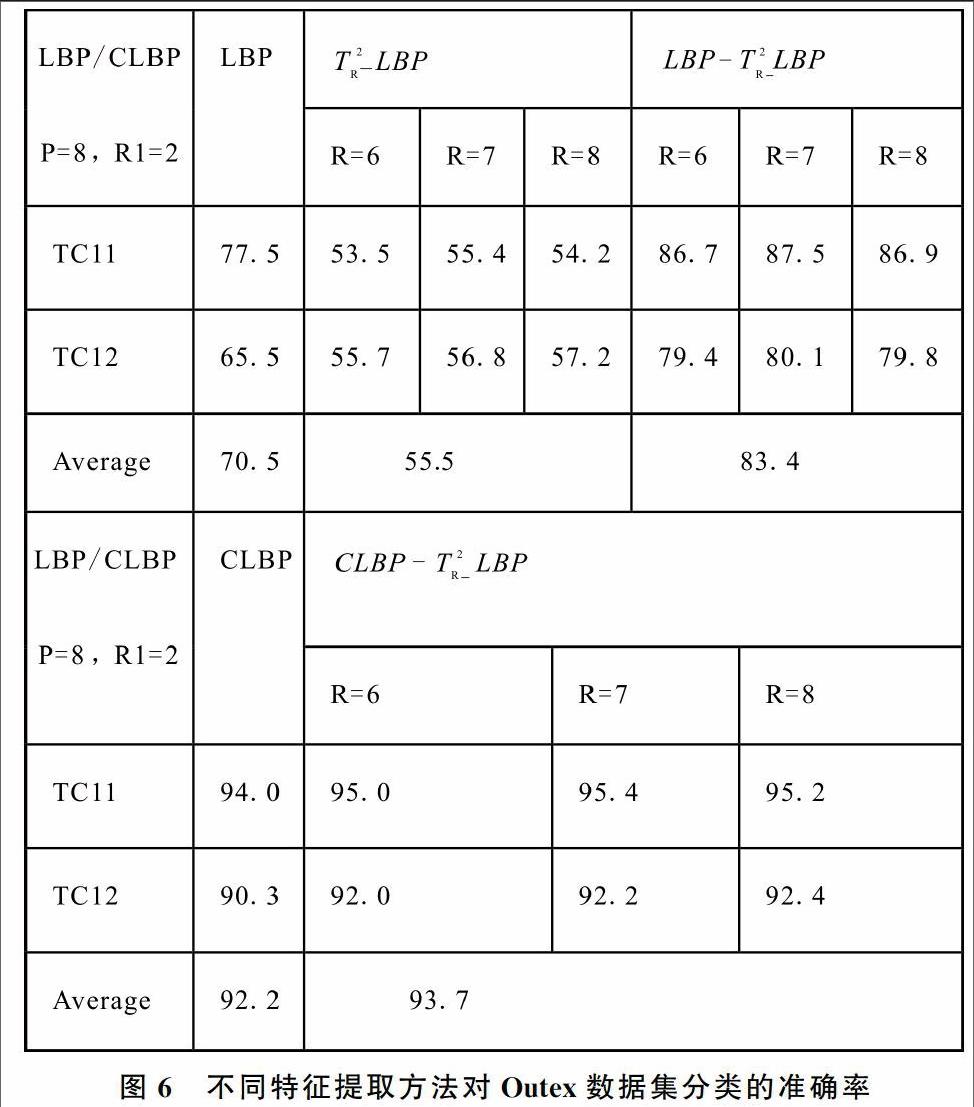
为了评价上述纹理特征提取方法的性能,在Outex数据库中的Outex_TC_00011和Outex_TC_00012数据集上做了一系列实验。其中,Outex_TC_00011数据集包含960个数据样本,Outex_TC_00012数据集包含了9 120个数据样本,通过对比不同特征提取方法的分类准确率来评价特征提取方法性能。其中实验中用到的特征提取方法有:LBP、T2R-LBP、LBP-T2R-LBP、CLBP及CLBP-T2R-LBP。分类方法选择最近邻原则,将测试图像归为差异度最小的那一类。分类准确率结果如图6所示。
根据图6不同尺度结构元素下特征提取方法的分类准确率看出,可以通过调节顶帽变换中的结构元素的半径尺度,可以得到能够取得较高分类准确率的特征;从表1中不同特征提取方法的平均分类准确率看出,单一的LBP和T2R-LBP的特征提取方法的平均分类准确率分别为70.5%和55.5%,准确率均不是很高,而LBP-T2R-LBP取得了83.4%的平均分类准确率,分类准确率有了大幅度提高。但相比于CLBP方法所取得的92.2%平均分类准确率,其分类准确率仍然逊色不少,然而CLBP-T2R-LBP却取得了93.7%的平均分类准确率,较CLBP的平均分类准确率有了小幅度提高。
5 结语
本文在前人研究的基础上对纹理特征提取方法展开了研究,提出了基于顶帽变换和LBP算子的多特征组合的纹理特征提取方法。经实验验证,该方法确实能够提高对Outex数据集分类的准确率,并可得出结论:特征提取方法应当遵循多特征组合、组合特征间差异大和组合特征维数小的原则。但本文仍然存在很多不足之处:虽然顶帽变换能够帮助提取出具有较强区分能力的图像分量,但其计算时间复杂度高,在实际应用中会受到一定的限制。因此,在能够得到具有高区分能力、计算时间复杂度低及特征维数低的描述方法方面有待进一步研究。
参考文献:
[1] 刘晓明.纹理研究及其应用综述[J].测控技术,2008,27(5):4-9.
[2] 纪君.基于MPEG-7纹理特征的医学图像检索技术研究[D].沈阳:沈阳工业大学,2010:13-16.
[3] 钟小勇.基于Curvelet变换和BP神经网络的织物疵点检测[D].苏州:苏州大学,2010.
[4] 丛家慧.引入人类视觉特性的带钢表面缺陷检测与识别方法研究[D].沈阳:东北大学2010:14-25.
[5] 过林.基于纹理特征的典型遥感影像面状地物提取方法研究[D].郑州:解放军信息工程大学,2011.
[6] 贺晓建,王福明.基于灰度共生矩阵的纹理分析方法研究[J].研究与探讨,2010(4):89-90.
[7] 王飞.复杂背景下条形码检测[D].西安:西安电子科技大学,2012.
[8] 黄媛媛.基于小波的纹理特征提取算法的研究[D].镇江:江苏科技大学,2011:13-55.
[9] 刘丽,匡纲要.图像纹理特征提取方法综述[J].中国图像图形学报,2009(4):3-8.
[10] STROMBERW D,FARR T G.A fourier based texture feature extraction procedure[J].IEEE Transaction Geosie-Remote Sensing,1986(24):722-731.
[11] CHENC C,HUANGC L.Markov random fields for texture classification[J].Pattern Recognition Letters,1993,14(11):907-914.
[12] 赵瑞珍.小波理论及其在图像、信号处理中的算法研究[D].西安:西安电子科技大学,2001:17-47.
[13] ZHANCHAO LI,XUAN ZHOU,ZONG DAI,et al.Class-ification of G proteins and prediction of GPCRs-G proteins coupling specificity using continuous wavelet transform and information theory[J].Amino Acids,2012,43(2):793-804.
[14] OJALA T.Multi-resolution gray-scale and rotation invariant texture classification with local binary patterns[J].IEEE Trans.on Pattern Analysis and Machine Intelligence,2002,24(7):971-987.
[15] 宋克臣,颜云辉,陈文辉,等.局部二值方法研究与展望[J].自动化学报,2013(6):3-6.
[16] 毋小省,朱世松,孙君顶.基于凹凸局部二值模式的纹理图像分类[J].光电子·激光,2014(4):3-8.
[17] 贺永刚.基于局部二值模式的纹理表达研究[D].武汉:华中科技大学,2012:27-58.
[18] BAI XIANGZHI,ZHOU FUGEN.Multiscale top-hat transform based algorithm for image enhancement[C].2010 IEEE 10th International Conference on Signal Processing(IC-SP),2010:797-800.
[19] 刘豪,杨永全,郭仙草,等.用于纹理特征提取的改进的LBP算法[J].图形图像处理,2014,50(6):182-185.
(责任编辑:孙 娟)

