A Temporal-Spatial Logic for Branching Space-times*
Hu Liu
Institute of Logic and Cognition,Sun Yat-sen Universityliuhu2@mail.sysu.edu.cn
A Temporal-Spatial Logic for Branching Space-times*
Hu Liu
Institute of Logic and Cognition,Sun Yat-sen Universityliuhu2@mail.sysu.edu.cn
.Branching space-times,which was proposed by(Belnap,1992),is a framework that generalizes branching time by introducing a space-like relation to“our world”.We present in this papera formallanguage to characterize properties ofbranching space-times.We use a space like operator to reflect the space-like relation.The paper focuses on a Hilbert style proof theory of temporal logic for branching space-times.We present some limited results of completeness.
1 Introduction
The focus of the present paper is a temporal logic for branching space-times, which goes back to[1].Different aspects of branching space-times have been studied in[2,3,9,10,11,12],which,from the pointofview oflogic,are allmodeltheoretical. We start in this paper to investigate a formal language of temporal-spatial logic for branching space-times.
Temporal logics are formalizasions of time.The simplest way to think of time in an abstract manner is to picture it as a line.Formally,it is a structure(T,<),whereTis a set of time points,and<is a linear order onT,i.e.<is(1)irreflexive,(2) transitive,and(3)trichotomous.This linear time(LT)picture is dominant in science and in most people’s minds.Some philosophers argue that indeterminism is indispensable to any theoretical framework of our world.So-calledbranching time(BT), which reflects the indeterminism,has received much attention from temporal logicians.A BT-structure is a flow of time without the condition(3)on<,and satisfies no backward branching:every point’s past is a linear order.Only branching to the future is allowed in branching time,which means that from a given point,the future may be undetermined,while the past is always determined.
Though richer than linear time,a branching time is still insufficient to capture some intuitive ideasabouttime,such asthe factthatsome eventsmay happen simultaneously at different places so that they have a space-like relation.Belnap’s branching space-time([1]),BST for short,is a framework that captures such properties of time,or space-time.It is a combination of indeterminism and relativistic space-times in a single structure.
Temporal logic is an active area of interest for decades.Many results have been known concerning temporal logics of branching time.There are two schools of branching time temporal logics:Peircean and Ockhamist.([13])Taking the future operatorFas an example,Peircean logic interprets the sentenceFαas“α will be true in every possible future.”Formally,letMbe a branching time model,ta point in it,andha history in this model(a maximal linear order).Then
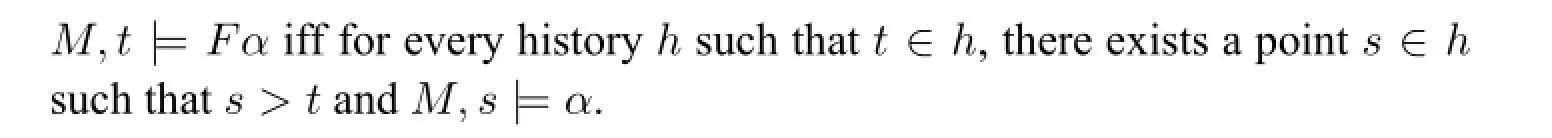
From the point of view of Ockhamist logic,it is meaningless to assign a truth value toFφat a pointtwithout specifying which history is concerned.The satisfaction relation in Ockhamist logic is defined as follows:

In Ockhamist logic,a historical possibility operator♢was introduced to express the manifoldness of the future.That♢αis true at a pointtin a historyhmeans thatαhappens attin some history passing throught.Formally,

The semantic rule for this♢involves quantification over histories so that it is not a Kripke-style semantics.In order to replace this second-order condition,some authors have suggested first-order alternatives:Thomason’sKamp frame([14]),Burgess’sBundled tree([5])and Zanardo’sOckhamist frame([15]).It has been proved that those frameworks are semantically equivalent.
Ockhamistlogic is strictly more expressive than Peircean logic,and has received much more attention than the latter.The logic defined in this paper is an Ockhamist style spatial-temporal logic.
2 Ockhamist BST structure
2.1Branching space-times and bundled worlds
We first introduce a version of branching space-times structure slightly different from the original one in[1].
Definition 2.1ABranching space-timestructure is a non-empty strict partial orderE=(E,≪).A subsethofEisdirectedif any paire1,e2∈hhave a common upper bound inh.Ahistoryis a maximal directed set.There are three postulates on BST structures:
(1)Weak Prior Choice Principle(WPCP):Suppose that two historiesh1andh2intersect ande1∈h1−h2.Then there exists ae2≪e1such thate2is a choice point ofh1andh2,that is,e2is a maximal point inh1∩h2.
(2)Incompatibility Principle(IP):Suppose thate1∈h1−h2,e2∈h2−h1,and there exists a choice pointesuch thate≪e1ande≪e2.Thene1ande2are incompatible,that is,e1ande2have no common upper bound.
(3)Weak Historical Connection(WHC):Ifh1∩h2/=Øandh2∩h3/=Ø,then
h1∩h3/=Ø.
WPCP says that for ane1∈h1−h2,the fact of it belonging to one history and not to the other history must happen for a reason.That is,a past choice pointe2that divided the two histories.IP guarantees that two histories that was divided by a choice points are indeed separated.
Throughout this paper we assume the languageL,whose alphabet consists of a countable set of propositional variablesp0,p1,...,Boolean connectives¬,→,and four modalitiesG,H,S,□.Letα,β,...range over formulas.Formulas are constructed as follows:

Other Boolean connectivesare defined asusual.GandHare temporaloperators with the respectively intended meaning“···will always be true”and“···has always been true”.□is the historical necessity modality with the intended meaning“···is true in any other history.”Sis a space-like operator that is read as“···is true at all space-like related points.”
LetF,P,D,♢be abbreviations for¬G¬,¬H¬,¬S¬,¬□¬respectively.LetAα=α∧Gα∧Hα∧Sα.Aαmeans thatαis true throughout the given history. LetEαstand for¬A¬α.
Given a BST structureE=(E,≪),we say thatU={(h,e):his a history inEande∈h}is theuniverseonE.Avaluation Vis a function assigning to each propositional variable a subset ofU.The definition ofV(α)for an arbitrary formulaαis as follows:
(1)V(¬α)=U−V(α).
(2)V(α→β)=V(¬α)∪V(β).
(3)V(Gα)={(h,e)∈U:∀e′∈h(e′≫e⇒(h,e′)∈V(α))}.
(4)V(Hα)={(h,e)∈U:∀e′∈h(e′≪e⇒(h,e′)∈V(α))}.
(5)V(Sα)={(h,e)∈U:∀e′∈h((e′/=e¬e′≪e¬e≪e′)⇒(h,e′)∈V(α))}.
(6)V(□α)={(h,e)∈U:∀h′((e∈h′&h′/=h)⇒(h′,e)∈V(α))}.
Clearly,□operator is different from the usual historical necessity operator used in branching time in that it corresponds an irreflexive relation over histories.The usual operator,say□′,can be incorporated into BST as follows:
·V(□′α)={(h,e)∈U:∀h′(e∈h′⇒(h′,e)∈V(α))}.
□′is definable by□as that□′α=□α∧α.The reverse does not hold.We use the more expressive□in order to characterize postulates of branching space-times.
Item(6)contains a quantifieroverhistoriesso thatitisnotKripke-style.In order to obtain a first-order condition and a Kripke-style semantics,we adopt the idea of“bundled tree”presented in[5].We use a similar notion namedbundled world.
Definition 2.2Abundled world Fis a pair(E,H),whereEis a BST structure andHis a bundle on it;that is,His a subset of the universeUonEsuch that(h,e)∈Himplies that for everye1∈h,(h,e1)∈H;and for everye∈E,there is at least one (h,e)∈H.
A valuation on a bundled world(E,H)assigns to each propositional variable a subset ofH.The notions of valuationV(α)for a formulaαcan be obtained by replacingUbyHin the above semantic definition,and replacing item(6)by item (6’),in which the quantifier is overH,instead of over histories.
(6’)V(□α)={(h,e)∈U:∀(h′,e)((e∈h′&h′/=h)⇒(h′,e)∈V(α))}.
2.2Ockhamist BST structure
In this section we introduce a Kripke structure defined on bundled worlds.The name of the structure,Ockhamist BST structure,comes from Zanardo’sOckhamist framefor branching time.Intuitively,each point in an Ockhamist BST structure is a first-order variable that can be thought of as ranging over pairs(h,e),where(h,e) is an element of the corresponding bundled world.We will show that the semantics defined on an Ockhamist BST structure is equivalent to the semantics defined on a bundled world.
Definition 2.3We say a tripleF=(W,<,∼)is a(basic)structureif W is a nonempty set,<and∼are two binary relations on W such that<is irreflexive and transitive,and∼is an equivalence relation.Letw1,w2,etc.,range overW.
Intuitively,ifw1,w2∈Wrespectively represent(h1,e1)and(h2,e2)in the corresponding bundled world,thenw1<w2implies thath1=h2ande1≪e2,andw1∼w2implies thate1=e2.
Definition 2.4(1)≤is the reflexive closure of<.
(2)w1andw2are connected,denoted byw1−cw2,is defined as that eitherw1=w2, orw1<w2,orw1>w2,orw1andw2have a common upper upper bound.w1/−cw2says thatw1is not connected tow2.We letC1,C2,...range over the set of maximal connected sets.
(3)w1−sw2is defined asw1−cw2,w1/=w2,not w1<w2andnot w2<w1.w1−sw2is read as thatw1isspace-like relatedtow2.

Definition 2.6[w]is achoice pointfor two maximal connected setsC1andC2if [w]intersects bothC1andC2,and there is no[w1]≫[w]such that[w1]intersects both of them.
Definition 2.7We say a structureF=(W,<,∼)is anOckhamist BST structurewhenever it satisfies all of the following statements:
(Dis)If w1∼w2,thennotw1<w2.
(Dismeans“Disjointness of<and∼.”)
(DH)If∃w(w<w1&w<w2),then∃w(w≥w1&w≥w2).
(DHmeans“Directedness of Histories.”)
(PI)If w1∼w2,then there exists an order-isomorphism f between{w:w<w1}and{w:w<w2}such that for all w<w1,w∼f(w).
(PImeans“Past Isomorphism.”)
(MH)If w1∼w2and w1/=w2,then∃w((w>w1)&∀w3((w3>w2)⇒notw∼w3)).
(MHmeans“Maximality of Histories.”)
(WHC)If∃w1∈C1∃w2∈C2(w1∼w2)and∃w2∈C2∃w3∈C3(w2∼w3),then∃w1∈C1∃w3∈C3(w1∼w3).
(WHCmeans“Weak Historical Connection”.)
(WPCP)If C1∩C2/=Ø,[w1]∩C1=w1,[w1]∩C2=Ø,then there exists a choice point[w]such that([w]∩C1=w)⇒w<w1.
(WPCPmeans“Weak Prior Choice Principle”.)
(IP)If w1∈C1,w2∈C2,[w1]∩C2=Ø,[w2]∩C1=Ø,and there exists a
choice point[w]for C1and C2such that[w]≪[w1]&[w]≪[w2],then
there does not exist a Csuch that[w1]∩C/=Ø&[w2]∩C/=Ø.
(IPmeans“Incompatibility Principle.”)
A structure having the propertyDiswill be called aDis-structure and similarly we shall refer toDH-structures,(Dis+DH)-structures and so on.
Lemma 2.8Given anOckhamist BST structure F=(W,<,∼),letE=(W/∼,≪)(≪is as defined in Def.2.5),andH={[C]|Cis a maximal connected set}. ThenEis a branching space-times,and(E,H)is a bundled world.
ProofSuppose that[w1]≪[w2]and[w2]≪[w3].By the definition of≪and the transitivity of<,[w1]≪[w3].Thus≪is transitive.
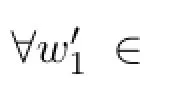
Now we show that every maximal connected setCinFreflects a history,i.e. [C]is a history inE.Suppose thatw1∈C,w2∈C,w∈C,and[w]≪[w1]and [w]≪[w1].By the definition of≪,there exists aw∈[w]such thatw<w1andw<w2.ByDH,there exists aw′∈Csuch thatw′≥w1&w′≥w2.ByPI, [w′]≫[w1]and[w′]≫[w2].Therefore[C]is directed.
Suppose thatw2is such that[w2]/∈[C1].We show that[C1]∪{[w2]}is not directed.Suppose otherwise.Then we must have that for anyw1∈C1,[w1]≪[w2],otherwise,by the definition of≪,[w2]∈[C1].w2must be in some maximal connected set,sayC2.Then[C1]⊂[C2],which contradictsMH.
ThatEsatisfies weak historical connection,weak prior choice principle and incompatibility principle is guaranteed byWHC,WPCPandIPrespectively.Thus,Eis a branching space-times.We have already shown that each[C]is a history inE. ThatHis a bundle follows fromCbeing a maximal connected set.□
The reverse of 2.8 also holds.The proof is omitted.
Lemma 2.9Given a bundled world((E,≪),H),letW={hi∩{e:e≫ej}:hi∈Handej∈hi};let<be the proper-superset relation⊃onW;letw1∼w2iffw1=hi∩{e:e≫ej}andw2=hl∩{e:e≫ej}for aejin E andhi,hl∈H. ThenF=(W,<,∼)is an Ockhamist BST structure.
From lemma 2.8 and 2.9,two relationsfandgcould be defined as follows:
·f((W,<,∼))=(E,H),where(W,<,∼)is an Ockhamist BST structure,
(E,H)is a bundled world as defined in lemma 2.8.
·g(((E,≪),H))=(W,<,∼),where((E,≪),H)is a bundled world,(W,<,∼)is an Ockhamist BST structure as defined in lemma 2.9.
Theorem 2.10(1)fandgare bijections;(2)for anyOckhamist BST structure F,gf(F)=F;(3)for any bundled world E,fg(E)=E.
Proof(1)iseasy to check.For(2),supposeF=(W,<,∼).Letf(F)=((W/∼,≪),H).Letg(((W/∼,≪),H))=(W′,<′,∼′).It is sufficient to show that (W′,<′,∼′)is the same structure as(W,<,∼),i.e.they are isomorphic.By the definition offandg,eachw′∈W′is of the form[C]∩{[wC]:[wC]≫[w]},and [C]∩[w]/=Ø.Define a functionτas follows:
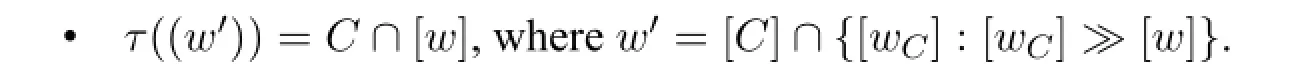

The proof for(3)is similar and omitted.□
Definition 2.11Amodel Mis a tuple(F,V),whereF=(W,<,∼)is anOckhamist BST structureandVis an valuation function assigning to each propositional variable a set of pointsW′⊆W.The definition ofV(α)for a formulaαis as followed:
·V(¬α)=W−V(α).
·V(α→β=V(¬α)∪V(β)).
·V(Gα)={w∈W:∀w1(w1>w⇒w1∈V(α))}.
·V(Hα)={w∈W:∀w1(w1<w⇒w1∈V(α))}.
·V(□α)={w∈W:∀w1((w1∼w&w1/=w)⇒w1∈V(α))}.
·V(Sα)={w∈W:∀w1(w1−sw⇒w1∈V(α)}.
Satisfaction and validity are defined asusual,and denoted byw|=φand|=φ.It is easy to see that the semantics on Ockhamist BST structures in 2.11 is semantically equivalent to the one defined on bundled worlds.
3 Axiomatizations of Ockhamist BST structures
3.1The axioms
Since the semantics defined on bundled worlds is equivalent to that defined on Ockhamist BST structures,we can now focus on Ockhamist BST Structure.
An Ockhamist BST structure is a basic structure plus the seven conditions in definition 2.7.The axioms contain those axioms of the basic temporal logic:
(A0)propositional calculus.
(A1-A4)G(p→q)→(Gp→Gq),H(p→q)→(Hp→Hq),
□(p→q)→(□p→□q),S(p→q)→(Sp→Sq).
(A5-A6)p→GPp,p→HFp.
As well known,there is no axiom for irreflexivity.For transitivity,we have
(A7-A8)Gp→GGp,Hp→HHp.
We have two axioms for the□operator:
(A9-A10)(□p∧p)→□□p,p→□♢p.
As for the space-like operatorS(D),the connectivity property seems stating an infinite condition,which state that,whereλis an ordinal,
The sentence is not a well formed formula.Fortunately,with the help ofDH,we could reduce it to a legitimate formula.Where two points are connected,byDHand an(transfinite)induction on number of steps that connect the two point,it can be verified that the two points must connect within two steps.Therefore,we can have the following axiom characterizing connectivity:
(A11)Dp→FPp.
Now we consider axioms for the seven additional conditions to basic structures. There is no corresponding axiom forDis,which is a version of irreflexivity ForDH, we have the following:
Lemma 3.1A basic structure is a DH-structure iff it validates(A12):
(A12)(Fp∧Fq)→(F(p∧q)∨F(p∧Pq)∨F(q∧Pp)∨F(Pp∧Pq)).
ProofThe point is that there are four cases for two pointsw1andw2to have a common upper bound.That is,the case whenw1=w2,corresponding toF(p∧q); the cases whenw1>w2orw1<w2,corresponding toF(p∧Pq)orF(q∧Pp);the case when∃w(w>w1&w>w2),corresponding toF(Pp∧Pq).□
Because axioms forthe otherconditionsdepend onWHC,we shalldiscussWHCfirst.
Lemma 3.2A basic structure is a WHC-structure iff it validates(A13):
(A13)E♢E♢Ep→(Ep∨E♢Ep).
ProofSuppose thata structure isaWHC-structure,andE♢E♢Epistrue ata pointwof the structure.LetC1be the maximal connected set such thatw∈C1.Because we do not haveDis,each time we encounter a♢operator,there are two possibilities: either stay within the current maximal connected set,or switch to another maximal connected set.Thus,we have four cases now.Assume thatC2andC3aresomemaximal connected sets.

Case(1)corresponds to the case that the first application of♢drags us fromC1toC2,and the second application of♢drags us fromC2toC3.There are two further subcases:(i)C1=C3.In this subcase we havew|=Ep,therefore satisfies(A13). (ii)C1/=C3.In this subcase,byWHC,∃w1∈C1∃w3∈C3(w1∼w3).Therefore,w|=E♢Ep,and satisfies(A13).
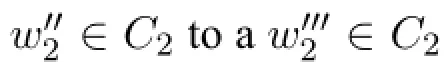
Case(4)corresponds to the case that both applications of♢stay withinC1.It is clear thatw|=E♢Epin this case.
The other direction is omitted.□
Validity of the following axioms depends onWHCas a precondition.
Lemma 3.3A WHC-structure is also a MH-structure,i.e.a WHC+MH-structure iff it validates(A14):
(A14)(Ap∧A□A¬p)→□F□¬p.
ProofSuppose that the structure being considered is aWHC+MH-structure,andAp∧A□A¬pis true at a pointw1in a maximal connected setC1.ByAp,we know thatpis true throughoutC1.ByA□A¬p,we know thatpis false throughout all other maximal connected setsCithat areaccessiblefromC1in the sense that there exists a[w′]such that[w′]∩C1/=Øand[w′]∩Ci/=Ø.
Lemma 3.4A WHC-structure is also a WPCP-structure iff it validates(A15):
(A15)(□p∧E♢(A¬p∧A□Ap))→P(♢¬p∧G□p).
ProofSuppose that the current history ish1and the current point isw1.The antecedent of A15 says that there is another historyh2such thatw1is not inh2andpis false inh2andpis true in all other histories includingh1.The consequent indicates that a choice point exists in the past ofw1.□
Lemma 3.5A WHC-structure is also a IP-structure iff it validates(A16):
(A16)(G□p∧♢(G¬p∧p∧Hp∧Sp∧A□Ap))→G□A□p.
ProofSuppose thatFisa WHC-structure and doesnotsatisfy IP.Then there are two maximalconnected setC1andC2and a choice point[w]forthem withw1∈[w]∩C1,w2∈[w]∩C2such that for a pointu>w1and a pointv>w2,there is a maximal connected setCthatintersectsboth[u]and[v].LetVbe a valuation such thatpistrue at all points except the pointsv′>w2.Then the antecedent of A16 is true at pointw1.Because there is aCthat intersects both[u]and[v],we know thatu|=♢E♢¬p. Thenw1|=F♢E♢¬p;that is,the consequent of A16 is not true atw1.A16 is not true atw1.The other direction is omitted.□
Let
(D)Gp→Fp.
The systemSconsists of axioms(D),(A1)-(A12)and the following rules:

Consider the set of allS-maximal consistent sets(MCSs).Define relations<Mand∼Mon this set as
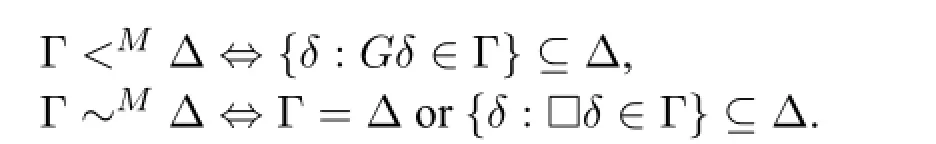
<Mcan be defined equivalently by Γ<MΔ⇔Δ⊆{δ:Fδ∈Γ}⇔{δ:Hδ∈Δ}⊆Γ⇔Γ⊆{δ:Pδ∈Δ};also,Γ∼MΔ is equivalent to(Γ=Δ or Δ⊆{δ:♢δ∈Γ}).
Lemma 3.6(1)IfFα∈Γ,then there exists a Δ such thatα∈Δ and Γ<MΔ.
(2)IfPα∈Γ,then there exists a Δ such thatα∈Δ and Γ>MΔ.
(3)If♢α∈Γ,then there exists a Δ such thatα∈Δ and Γ∼MΔ.
(4)IfDα∈Γ,then there existsaΔsuch thatα∈Δ,andΓandΔare connected by<M.
Lemma 3.7If Δ<MΓ and Δ<MΓ′,then there exist a Σ such that Γ<MΣ and Γ′<MΣ.
It can be verified that the relation∼Mis an equivalence relation on the set of MCSs;and<Mis transitive.However,<Mis not irreflexive in general.Note that the relation corresponds to♢is also irreflexive.We use the methodelimination of counterexamples([6,7])in the proof.
Definition 3.8(1)A chronicle on a structureFis a function C assigning each point ofFa MCS and satisfying
for allv,winF,v∼w⇒C(v)∼MC(w)andv<w⇒C(v)<MC(w)
(2)A chronicle onFis full whenever,for every point w,
(a)Fα∈C(w)⇒∃v(w<v&α∈C(v));
(b)Pα∈C(w)⇒∃v(w>v&α∈C(v));
(c)♢α∈C(w)⇒∃v(w∼v&w/=v&α∈C(v));
(d)Dα∈C(w)⇒∃v(w−sv&α∈C(v)).
Given a chronicleConF,define a valuationV:w∈V(p)⇔p∈C(w).By induction on the structure of a formulaα,it can be shown that ifCis full,then for every pointw,w∈V(α)⇔α∈C(w).Then,proving a given set of formulas Γ satisfiable is equivalent to proving that there exists a structureFand a full chronicleCon it such that Γ⊆C(w)for somewinF.
Given a structureFand a chronicleCon it,we say that(w,Fα)is a counterexample in the chronicleCwhenever the right side of 3.8(2)a is false for(w,Fα).The cases for(w,Pα),(w,♢α),(w,Dα)are similarly defined.
The eliminability of counterexamples is based on the following lemma.
Lemma 3.9IfCis a chronicle on a finite DH-structureFand(w,Fα)is a counterexample,then there exists a finite DH-structureF′⊇Fand a chronicleC′on it such that(w,Fα)is not a counterexample inC′.Similarly,we can eliminate the counterexample of the form(w,Pα),(w,♢α),or(w,Dα).
ProofSuppose that(w,Fα)is a counterexample in the chronicleConF.By lemma 3.6,there exists a Δ such thatα∈Δ and Γ<MΔ.We extendFto a structureF′by adding a new pointxtoFand by extending<and∼to<′and∼′:<′is the smallest strict partial order containing<and such thatw<′x;∼′=∼∪(x,x). The chronicleCis extended to a chronicleC′onF′by assigning Δ tox.(w,Fα)is not a counterexample in the chronicleC′onF′.The elimination of a counterexample (w,Pα)is similar to that of(w,Fα).
Let(w,Dα)be a counterexample in the chronicleConF.By axiom A11,FPα∈C(w).If(w,FPα)is not a counterexample,letF′′=F,C′′=C,andx′′be a point such thatx′′>wandPα∈C(x′′);if(w,FPα)is a counterexample,then we extendFto a structureF′′andCto a chronicleC′′with(w,FPα)eliminated by adding a new pointx′′and assigning a Δ tox′′such thatPα∈Δ.
Regardless of whether or not(x′′,Pα)is a counterexample in the chronicleC′′, we extendF′′to a structureF′by adding a new pointx′,and extending<and∼inF′′to<′and∼′:<′is the smallest strict partial order containing<and such thatx′<′x′′;∼′=∼∪(x′,x′).By lemma 3.6(2),we extend chronicleC′′to a chronicleC′onF′by assigning a Δ tox′such thatα∈Δ and Δ<MC′(x′′).By the above construction,x′is a space-like related point tow.
The elimination of(w,♢α)uses lemma 3.6(3)to add a pointxtoFand extendCtoC′by assigning Δ tox,whereα∈Δ and Δ∼MC(w).The relations are extended as<′=<and∼′=∼∪{(x,x),(x,w),(w,x)}.
In general,the structureF′obtained by the elimination of(w,Fα),(w,Pα), (w,Dα),or(w,♢α)is not a DH-structure.In that case,guided by lemma 3.7,we can extendF′to a DH-structure and extendC′to a chronicle on that structure.Then we get a DH-structure and a chronicle on it such that(w,Fα)[(w,Pα),(w,Dα),or (w,♢α)]is not a counterexample.□

Theorem3.11The systemSisstrongly complete with respectto the family ofrightserial DH-structures.
Fas defined in 3.10 is actually a Dis-structure.Thus,we have that
Theorem 3.12The systemSis strongly complete with respect to the family of right-serial(Dis+DH)-structures.
ProofEvery consistent set is extendable to a maximal consistent set by standard techniques.It is sufficient to show that for every maximal consistent set Γ,there exists a right-serial DH-structureFand a full chronicleCon it such that Γ=C(v) for somevinF.
LetF0be the DH-structure that contains only one elementw0such that<0is an empty relation,and∼0={(w0,w0)},andC0is a chronicle onF0such thatC0(w0)=Γ.Letα0,...,αn,...be a chain of all formulas of the formFα,Pα,Dα,or♢αin which each formula occurs infinitely often.Define a sequence of DH-structuresF0,...,Fn,...,with respective chroniclesC0,...,Cn,...,such that for eachi,all counterexamples(v,αi)inCiare eliminated inCi+1.Lemma 3.9 guarantees that such a sequence exists.LetF=∪i∈ωFiandC=∪
i∈ωCi.By lemma 3.10,Fis a DH-structure andCis a chronicle on it.BecauseF(p∨¬p)is in every member of chronicalC,there does not exist a dead end inF.Otherwise,F(p∨¬p) is an counterexample in that dead end,and will be eliminated in the sequence we constructed.
It remains to show thatCis full.Suppose otherwise.That is,suppose that there exists a counterexample(v,α)inC.By the construction ofC,(v,α)is a counterexample in finitely manyCn.Becauseαoccurs infinitely often in the sequence,(v,α) will be eventually eliminated.Thus(v,α)is not a counterexample inC.□
Now we focus on other postulates of Ockhamist BST structures.The following is a list of axioms.
LetS′be the system obtained by extendingSwith axioms A13-A16.we have that
Theorem 3.13The systemS′is strongly complete with respect to the family of right-serial(Dis+DH+WHC+MH+IP+WPCP)-structures.
S′is not a system for Ockhamist BST structures.There remains the postulate PI to be dealt with.The problem is still open.Considering the following axiom:
(A18)H□p→□Hp(To reflect PI)
API-structure doesnotvalidate the axiom.To do so anothercondition hasto be added to the PI-structure.The following lemma from[8]also holds in BST:
Lemma 3.14A structureFvalidates A18 iffFis irreflexive and satisfies PI.
There are some other important properties which we do not take as postulates of Ockhamist BST structures.Concerning the application of BST(see[2],[3]),such properties may include
(1)Density:Ifw1<w2,then there exists aw3such thatw1<w3andw3<w2.
(2)Infima:Every nonempty lower bounded chain has an infimum;that is,a maximal lower bound.
(3)Weak No Funny Business:Ifw1andw2are two space like related points such thatw1∈C1andw2∈C2,then there exists a maximal connected setC(a history)such thatw1∈Candw2∈Candw1(andw2)is not a choice point forCandC1(andC2).
(4)Chain Choice Principle:If a lower bounded chainXis inC1−C2,then there exists a choice point forC1andC2lying in the past ofX.
The axiomsthatcan be characterized by density,infima and weak no funny business are respectively
(1)Fp→FFp
(2)(F(p∧Sp)∧F(G¬p∧¬p))→F(HFp∧G¬p)
(3)(G□p∧♢DG□q)→♢(Fp∧DFq)
Verification of validity of the three formulas is omitted.We have not found an axiom for the chain choice principle yet.
The Ockhamist BST structure is semantically equivalent to the bundled world defined in Def.2.2,in which the bundle may not contain all possible histories in the structure,which Belnap calledmissing historiesin[4].Considering the BST structure without reference to bundles,or in other words,the bundled world of which the bundle containsallpossible histories,we may callita complete OckhamistBSTstruc-ture.Clearly,a complete system for the complete Ockhamist BST structure should include all A1-A6 as its theorems.However,the complete Ockhamist BST structure is not semantically equivalent to the Ockhamist BST structure.The Burgess’s formula,□G♢F□p→♢GFp([15]),suffices to show that.This formula is valid in the classofcomplete OckhamistBSTstructures,butisnotvalid in the classof Ockhamist BST structures.
In conclusion,as indicated,several problems remain.What has been accomplished here isto connecta prooftheory with the BSTOckhamistsemantics.A spacelike operator is defined and a system for the operator is given.The resultant temporal logic therefore is a temporal-spatial logic.
[1]N.Belnap,1992,“Branching space-time”,Synthese,92(3):385–434.
[2]N.Belnap,2002,“EPR-like funny business in the theory of branching space-times”, in T.Placek and J.Butterfield(eds.),Non-locality and Modality,pp.293–315,Kluwer Academic Publishers.
[3]N.Belnap,2005,“A theory of causation:Causae causantes(originating causes)as inus conditions in branching space-times”,The British Journal for the Philosophy of Science,56(2):221–253.
[4]N.D.Belnap,M.Perloff and M.Xu,2001,Facing the future:Agents and Choices in Our Indeterminist World,Oxford University Press.
[5]J.Burgess,1979,“Logic and time”,Journal of Symbolic Logic,44(4):566–582.
[6]J.Burgess,1980,“Decidability for branching time”,Studia Logica,39(2):203–218.
[7]J.Burgess,1982,“Axioms for tense logic I:‘Since’and‘Until’”,Notre Dame Journal of Formal Logic,23:367–374.
[8]D.Gabbay,I.Hodkinson and M.Reynolds,1994,TemporalLogic:MathematicalFoundations and Computational Aspects,Volume I,Oxford University Press.
[9]T.Kowalski and T.Placek,2000,“GHZ theorems in the framework of outcomes in branching space-time”,International Journal of Theoretical Physics,39(3):765–775.
[10]T.Müller,2005,“Modeling modal talk in quantum mechanics”,International Journal of Theoretical Physics,44(4):375–383.
[11]T.Müller,2005,“Probability theory and causation:Abranching space-times analysis”,The British Journal for the Philosophy of Science,56(3):487–520.
[12]T.Placek,2000,“Stochastic outcomes in branching space-time:Analysis of Bell’s theorem”,The British Journal for the Philosophy of Science,51(3):445–475.
[13]A.Prior,1967,Past,Present and Future,Oxford University Press.
[14]R.Thomason,1984,“Combinationsoftense and modality”,in D.Gabbay and F.Guenthner(eds.),Handbook of Philosophical Logic,Vol.2,pp.135–165,D.Reidel.
[15]A.Zanardo,1996,“Branching-time logic with quantification over branches:The point of view of modal logic”,Journal of Symbolic Logic,61(1):1–39.
分支时空结构上的时空逻辑
刘虎
中山大学逻辑与认知研究所liuhu2@mail.sysu.edu.cn
Belnap通过在分支时间结构上添加空间关系,提出了更一般化的分支时空结构。在本文中,我们首次为这种分支时空结构建立相应的逻辑系统。在该逻辑中,我们引入一个空间模态算子来表达模型中的空间关系。我们给出该逻辑的公理系统,并证明它的完备性。
Received2016-05-09
*I would like to thank Nuel Belnap for his detailed reading of the earlier version of this paper and numerous pertinent comments and criticisms.This research is supported by NSSFC Grant(14ZDB015) and the National Fund of Social Science(13BZX066).

