基于虚功原理的系泊系统重物球的确定

何 帆， 陈 锦, 刘馨文, 周宏敏

(1. 湖南理工学院 数学学院, 湖南 岳阳 414006; 2. 湖南理工学院 信息与通信工程学院, 湖南 岳阳 414006)

基于虚功原理的系泊系统重物球的确定

何 帆1， 陈 锦1, 刘馨文2, 周宏敏2

(1. 湖南理工学院 数学学院, 湖南 岳阳 414006; 2. 湖南理工学院 信息与通信工程学院, 湖南 岳阳 414006)

引入广义坐标和虚功原理建立了系泊系统达到平衡时的基本模型, 给出了各部件的倾斜角与作用力满足平衡条件时的方程组. 通过建立非线性规划模型计算出风速为12m/s和24m/s时的相关参数, 并计算出在风速为36m/s且满足钢桶倾斜角小于5°和锚链与海底平面夹角不超过16°的条件下重物球的设计要求.

系泊系统; 广义坐标; 虚功定理; 非线性规划模型

1 问题背景

近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成. 某型传输节点的浮标系统可简化为圆柱体. 系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成. 锚链选用无档普通链环.钢管共4节, 每节长度1m. 要求锚链末端与锚的连接处的切线方向与海床的夹角不超过16°. 水声通讯系统安装在一个密封圆柱形钢桶内. 钢桶上接第4节钢管, 下接电焊锚链.钢桶竖直时, 水声通讯设备的工作效果最佳. 若钢桶倾斜,则会影响设备的工作效果. 钢桶的倾斜角度超过5°时, 设备的工作效果较差. 为了控制钢桶的倾斜角度, 钢桶与电焊锚连链接处可悬挂重物球.

系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量, 使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小.

图1 观测网的传输节点示意图

问题1 某型传输节点选用II型电焊锚链22.05m, 选用的重物球的质量为1200kg. 现将该型传输节点布放在水深18m、海床平坦、海水密度为1.025×103kg/m3的海域. 若海水静止, 分别计算海面风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域.

问题2 在问题1的假设下, 计算海面风速为36m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域. 请调节重物球的质量, 使得钢桶的倾斜角度不超过5°, 锚链在锚点与海床的夹角不超过16°.

上述为2016年高教社杯全国大学生数学建模竞赛A题中的两个问题.

2 问题分析与假设

本文对于问题一和问题二可采用广义坐标建立虚功平衡方程, 考虑整个系泊系统处于静态平衡时,系统的每个部件都是处于平衡状态. 由虚功原理可知: 在理想约束条件下, 作用于该系统的所有主动力的虚功之和等于零. 故可以利用广义坐标建立虚功平衡方程, 从而得到各部件倾角和受力关系. 再利用这些关系作为约束条件来建立非线性规划模型, 并对模型进行求解, 最终确定相关参数.

模型的假设: (1) 海底水平; (2) 风向水平且恒定; (3) 各部件衔接处光滑; (4) 各部件均为密度均匀的物体.

3 虚功原理

在风向和风力为恒定时, 近浅海观测网的传输节点最终会处于平衡状态, 该平衡状态可以认为是平面问题. 在假设部件连接处都是光滑连接的情况下, 本系统可视为理想约束条件下处于平衡状态的动力系统. 本文所研究的问题也就变成了动力系统在平衡状态下的问题.

分别用a表示浮标,bj表示钢管第j节钢管,c表示钢桶,di表示锚链第i节锚链,e表示重力球. 这里所考虑的主动力包括: 近海面风力Ff, 每个部件的重力(用G和部件的标号作下标表示), 海水对整个系统的浮力(用F和部件的标号作下标).每个部件所受主动力及建立坐标系如图2所示.

浮标在风力的作用下倾斜时, 浮标吃水深度h定义为海平面与浮标中心轴的交点到浮标的底面圆的中心的距离, 如图3所示.

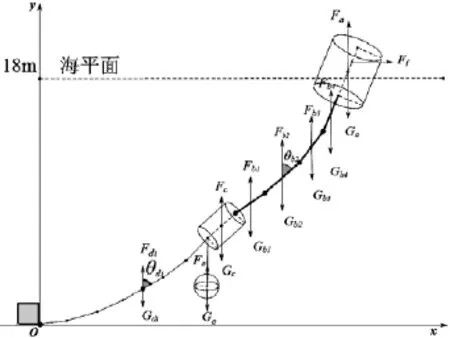
图2 坐标及作用力

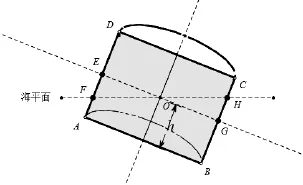
图3 吃水深度示意图

图4 水上浮子部分沿风的法向方向投影

图5 水下浮子部分

4 问题一的求解

从(5)中可以看出, 自变量数比方程组中方程的个数多一个, 所以该方程组无法求解. 浮标重心的y坐标ya还需要满足条件: 浮子的重心纵坐标ya减去到水面的距离等于水深18m. 根据几何关系可以得到

联立(5)和(8)求解方程组, 可确定各个参数. 由于该非线性方程组的求解非常困难, 这里以(8)为目标建立优化模型:

其中约束条件为(5)式.

为了简化求解, 将(5)中条件里除了θa的所有角度代入目标函数, 即可简化为非线性规划模型:

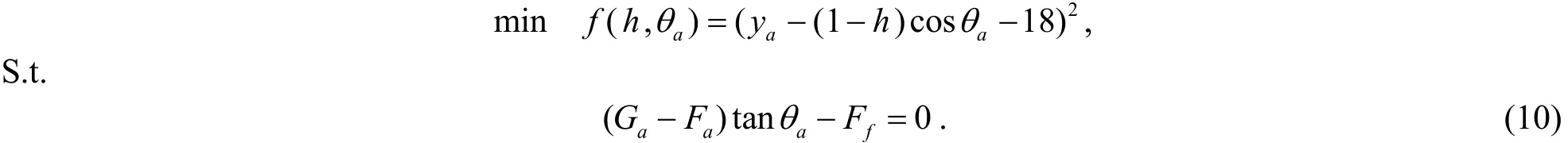
这样简化了运算, 通过Matlab2010R版本编写最优化求解程序, 分别设置风速为12m/s和24m/s, 求得结果见表1, 锚链形状如图6所示. 在风速为12m/s时, 锚链大约有6m的长度拖地.

表1 各参数结果

图6 锚链形状

5 问题二的求解

利用问题一的模型, 可计算得出海面风速为36m/s时各参数的值见表1. 从计算的结果可以看出, 当风速达到36m/s时, 钢桶的倾角达到了9.4463 °, 锚点与海底平面夹角达到了20.9669°, 明显不满足钢桶的倾角不超过5°和锚点与海床夹角不超过16°的要求. 为了满足该要求, 可增加重物球的重量. 因而这里将重物球的重力Ge作为变量, 建立优化模型求解. 要求钢桶的倾斜角度不超过5°, 转换成弧度, 即

锚链在锚点与海床的夹角不超过16°, 即第一个锚链倾角θd1不小于74°, 即

考虑需要求得满足条件(11)和(12)的最小质量, 本问题需要以|Ge|达到最小为目标, 由此可建立问题二的非线性规则模型:

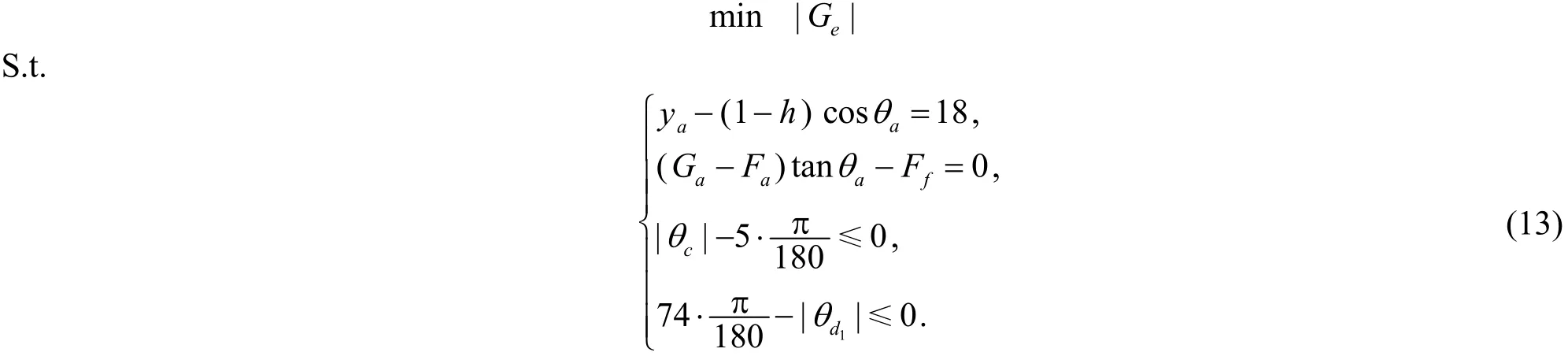
通过编写非线性规划模型求解得到重物球的最小重力Ge=-23512.88N, 转换成质量, 即重物球为质量为2399.27kg. 此时,钢桶的倾角为4.2292°, 锚点与海床的夹角为16°, 浮标吃水深度为1.0334m. 这说明钢桶倾角约束是无效约束, 而锚点处第1节锚链与海床夹角是紧约束. 锚链的形状如图7所示.

图7 36m/s风速下锚链形状

由此可得当风速达到36m/s时, 满足要求的重物球, 重量的设计不能小于2399.27kg.

6 总结

本文中采用了广义坐标建立了平衡方程, 利用虚功原理避免了传统复杂的受力分析, 并很容易得到了各部件倾角和作用力在静止平衡时的约束方程组, 广义坐标与所求的参数相符, 意义直观.

在问题一求解中, 引入海面高度和坐标关系作为目标函数, 用虚动原理得到的平衡方程作为约束条件进行求解, 得到了相关参数. 求解问题二中使用重物球的重力的绝对值作为目标函数, 通过位置平衡约束, 高度约束和角度约束, 建立非线性规则模型, 求解得出了满足条件的最小重物球重量. 如果考虑了水流力的情况, 如何通过优化选择锚链类型, 长度及重物球的重力是今后继续考虑的问题.

[1] 王振发. 分析力学[M]. 北京: 科学出版社, 2002: 1～25

[2] 哈尔滨工业大学理论力学科研室. 理论力学[M]. 第7版. 北京: 高等教育出版社, 2009

[3] 潘 斌. 浮标系泊系统静力计算[J]. 重庆交通学院学报, 1997,16(1): 68～73

Determination of Heavy Ball in Mooring System Based on Virtual Work Principle

HE Fan1, Chen Jin1, Liu Xinwen2, Zhou Hongmin2
(1.College of Mathematics, Hunan Institute of Science and Technology, Yueyang 414006, China; 2. College of Information and Communication Engineering, Hunan Institute of Science and Technology, Yueyang 414006, China)

In this paper, the basic model of the mooring system was established using introducing the principle of generalized coordinates and virtual work principle, and the equation group was given when the inclination angle and the force of each component meet the equilibrium condition. The system parameters were calculated by a nonlinear programming model with wind speed in 12m/s and 24m/s. When wind speed is 36m/s, minimum weight of the heavy ball is calculated to meet the requirements of the given angle.

mooring system, generalized coordinates, virtual work principle, nonlinear programming model

O221.2

: A

: 1672-5298(2016)04-0001-05

2016-08-23

何 帆(1978− ), 男, 湖南郴州人, 硕士, 湖南理工学院数学学院讲师. 主要研究方向: 数据分析