基于ABAQUS二次开发平台的边坡有限元强度折减法研究

候 玲， 薛海斌， 周泽华， 刘海伟， 潘 峰

(1.西安理工大学 理学院，陕西 西安710054；2.西安理工大学 岩土工程研究所，陕西 西安710048)



基于ABAQUS二次开发平台的边坡有限元强度折减法研究

候 玲1， 薛海斌2， 周泽华2， 刘海伟2， 潘 峰2

(1.西安理工大学 理学院，陕西 西安710054；2.西安理工大学 岩土工程研究所，陕西 西安710048)

有限元强度折减法在边坡稳定性分析中发挥着举足轻重的作用，但通常的有限元强度折减法采用二分法来获取边坡的安全系数，该方法需要多次试算，效率较低。本文借助ABAQUS软件的二次开发平台UFIELD程序，将软件自带的场变量定义为折减系数，建立场变量分别与软件求解时步和强度参数的关系，方便地实现了基于场变量的边坡有限元强度折减法，此方法仅需一次提交计算分析便可高效地实现边坡安全系数的求解；在基于场变量的边坡有限元强度折减法基础上，依据滑面位置处的等效塑性应变最大这一基本原理，利用不同垂直剖面逐点搜索法，实现了基于最大等效塑性应变的边坡潜在滑动面位置精细化寻找；最后借助两个经典算例，将此套思路确定的潜在滑动面位置、安全系数分别与传统极限平衡M-P法的对应结果进行对比分析，验证了本文思路和方法的有效性。

边坡有限元强度折减法； 场变量； 最大等效塑性应变； 潜在滑动面

有限元强度折减法在确定边坡安全系数的同时还可以方便地确定出边坡的滑动面位置，是边坡稳定性分析中的一种重要方法。

自从Zienkiewicz O.C.[1]等提出有限元强度折减法以来，唐芬[2]、Yuan W.[3]、薛海斌[4]等提出了不同的强度折减方式；杨光华[5]、薛雷[6]和陈国庆[7]等对边坡强度折减的范围进行了研究；张鲁渝、郑颖人[8]等研究了不同屈服准则对强度折减安全系数的影响，并试图探讨这些安全系数之间的关系；郑宏[9]、张培文[10]、杨光华[11]等分别提出了强度折减过程中其它配套参数的折减方式；宋二祥[12]、Griffiths D.V.[13]和连镇营[14]分别提出了三种不同的边坡失稳判据。总之，国内外学者在强度折减法研究方面取得了丰硕的成果，但是这些学者大都通过人为地对强度参数进行折减试算直到边坡失稳来确定边坡的安全系数，每次折减都必须提交一次计算分析，过程繁复。为了在保证计算精度的同时，简化此计算过程，曹先锋[15]、李宁[16]等分别提出了边坡稳定分析的温控参数折减有限元法和基于优化理论中的二分法来确定边坡的安全系数。

除边坡安全系数的确定之外，边坡稳定性分析的另一个关键问题就是滑面的确定。事实上强度折减法中给出的是滑动面位置所处的范围而未能精确到一条曲线。在强度折减法计算结果基础上，孙冠华等提出了基于等效塑性应变的边坡滑动面搜索方法[17]；李剑在此基础上借助FLAC3D软件内置的FISH语言实现了基于最大剪应变增量的边坡潜在滑动面搜索方法[18]；这些成果给出了确定滑动面位置的方法，但是很少在非均质边坡工程中应用。

本文拟借助ABAQUS的二次开发平台UFIELD程序，将软件自带的场变量定义为折减系数，建立场变量分别与软件求解时步和强度参数之间的关系，来实现基于场变量的有限元强度折减法，此方法仅需一次提交计算分析便可确定边坡的安全系数，较其它方法大大地提高了有限元强度折减法求解边坡安全系数的效率；以此为基础，依据滑面位置处的等效塑性应变最大这一基本原理，利用不同垂直剖面逐点搜索法，基于等效塑性应变对临界状态滑动面位置进行精细化寻找，给出了边坡滑动面的准确位置；最后借助算例验证了本文方法的有效性。

1 基于ABAQUS二次开发平台的边坡有限元强度折减法的基本原理

1.1 边坡有限元强度折减法的基本原理

边坡有限元强度折减法的基本原理就是通过不断减小材料强度参数直到边坡失稳，其临界状态对应的折减系数被定义为安全系数：

(1)

(2)

式中：SRF为折减系数；cini和c分别为折减前、后的黏聚力；φini和φ分别为折减前、后的内摩擦角。

1.2 基于场变量的有限元强度折减法的基本原理

为了后续确定边坡安全系数的方便，将场变量定义为折减系数:

f=SRF

(3)

上述确定了场变量与折减系数之间的关系，于是材料参数与场变量的关系如下：

(4)

(5)

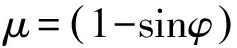
定义场变量与当前分析步的时步之间的关系为：

f=a+bt

(6)

那么，由式(3)可得：

SRF=a+bt

(7)

通常情况下:t取为当前分析步的时步，于是0≤t≤1；a参数决定着边坡的初始折减系数，取为1；a+b参数决定着折减系数的范围，为了计算的方便，b取为1；这样将折减系数的范围限定在[1,2]的闭区间内，但如若想增大折减系数的范围则可以通过增大b值来实现，具体a、b的取值视具体情况而定。

通过上述材料参数、场变量、计算时步及折减系数之间的相互关系，将基于场变量的有限元强度折减法基本原理归纳为：通过边坡弹塑性分析中计算时步的增加，借助计算时步与场变量的关系，得到场变量，借助场变量与材料参数之间的关系来更新材料参数，通过场变量和折减系数之间的关系确定当前的折减系数，那么边坡失稳时刻的折减系数即边坡的最终安全系数。对于基于场变量的有限元强度折减法，本文采用ABAQUS二次开发平台上的UFIELD程序来实现。具体程序接口和变量说明如下：

SUBROUTINE UFIELD(FIELD,KFIELD, NSECPT,KSTEP,KINC,TIME,NODE,

1 COORDS,TEMP,DTEMP,NFIELD)

C

INCLUDE ‘ABA_PARAM.INC’

C

DIMENSION FIELD(NSECPT,NFIELD), TIME(2), COORDS(3), KSTEP, KINC

1 TEMP(NSECPT), DTEMP(NSECPT)

C

user coding to define FIELD

RETURN

END

其中：FIELD表示场变量；KFIELD表示用户自定义场变量数；NFIELD表示更新的场变量数； KSTEP 表示分析步数；KINC 表示增量步数；TIME(1)表示当前时间步的时间；TIME(2) 表示总时间步的时间；NODE 表示节点数；COORDS 表示存放节点坐标的数组；TEMP(NSECPT) 表示所有节点的当前时刻温度；DTEMP(NSECPT)表示节点处的温度增量。

常规有限元强度折减法确定边坡安全系数的流程见图1(a)，从流程图中可以发现，首先给边坡赋予初始的抗剪强度参数，对边坡进行弹塑性分析，然后判断边坡是否失稳，如果边坡失稳则减小折减系数，重复上一步的计算；如果边坡未失稳则增大折减系数，重复上一步计算；如此反复从而求得边坡的安全系数。这样必须提交n次计算才能获得边坡的安全系数。而基于场变量的有限元强折减法计算边坡安全系数的流程如图1(b)所示，在ti时刻各节点达到平衡后时间步向前推进，随着时间步的增加，强度参数不断地折减，直到边坡的塑性区贯通和特征点水平位移随时间步的变化曲线出现拐点[19]，最终计算中断。这样仅需要一次提交计算便可以求取边坡的强度折减安全系数。

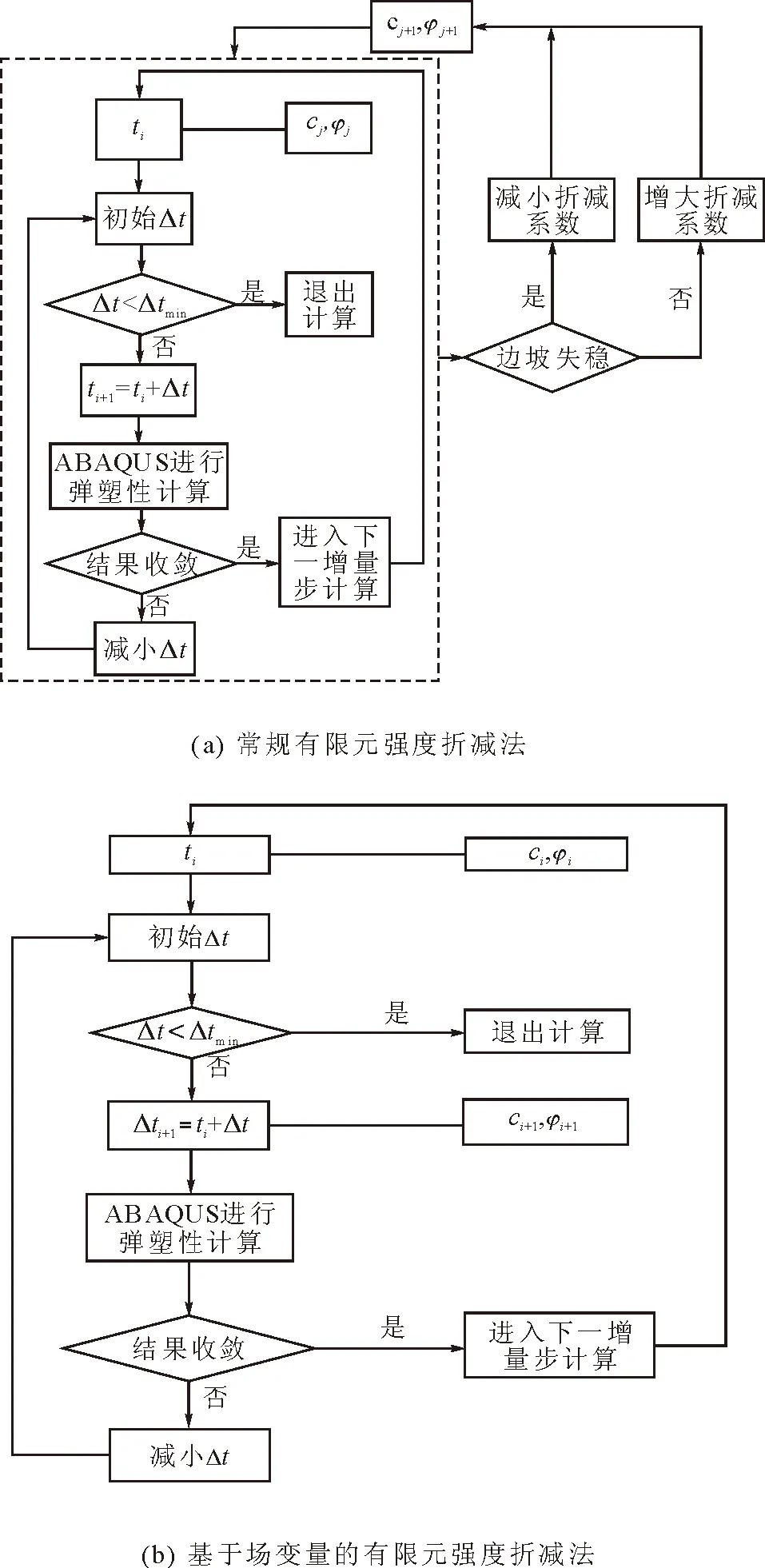
图1 常规有限元强度折减法和基于场变量的有限元强度折减法确定边坡安全系数的对比分析流程图Fig.1 Flow chart for calculating safety factor of slope using traditional strength reduction FEM and strength reduction FEM based on field variable

2 基于最大等效塑性应变的边坡潜在滑动面精细化寻找方法

在基于场变量的边坡有限元强度折减方法计算所得等效塑性应变的基础上，依据滑面位置处的等效塑性应变最大这一基本原理，可以实现一次自动搜索出边坡的潜在滑动面位置。依据最大等效塑性应变寻找边坡潜在滑动面的方法如下，首先在水平方向布置一系列的垂直线(见图2中点划线)，按照一定的空间步长分别在每一条垂直线上寻找等效塑性应变的最大值，将每条垂直线上等效塑性应变最大值点相对应的坐标点记录(见图2红色实心点)，并依次将这一系列点连线从而形成边坡临界滑动面的雏形，接着利用6次多项式采用最小二乘法将临界滑动面进行光滑化处理，便可以得到最终的边坡潜在滑动面。特别注意上述在等效塑性应变插值过程中采用等参元形函数进行插值，而且水平向与垂直向布点的个数决定着边坡滑动面位置的精确程度。实际计算中，可以先拟定出滑动面的大体位置，然后对初拟的滑动面位置附近的搜索步长进行加细，可以起到既节省时间又提高精度的效果。

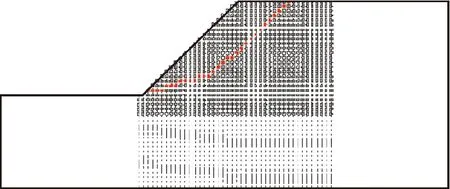
图2 基于最大等效塑性应变的边坡潜在滑动面精细化寻找方法示意图Fig.2 Potential slip surface of the slope is determined by the maximum equivalent plastic strain

3 有限元强度折减法二次开发程序的算例验证及滑动面精细化寻找方法的验证

本文基于ABAQUS二次开发平台UFIELD程序开发了基于场变量的有限元强度折减法，为了验证该方法的合理性及其基于最大等效塑性应变的滑动面精细化寻找方法的可靠性，分别选取均质、非均质两个边坡作为研究对象，将极限平衡M-P法计算结果作为衡量计算结果可靠性的标准。极限平衡M-P法[20]借助Geostudio软件的SLOPE/W模块来实现。

3.1 均质边坡算例分析

图3所示均质边坡坡高20m，坡比为1∶1，模型总高度为40m，总宽度为105m；有限元计算模型共离散为5773个单元，5938个节点；计算模型两侧采用水平向约束边界，模型底部采用全约束边界[21]。计算中采用考虑Mohr-Coulomb强度准则的理想弹塑性模型,具体计算过程中所采用的材料参数见表1。

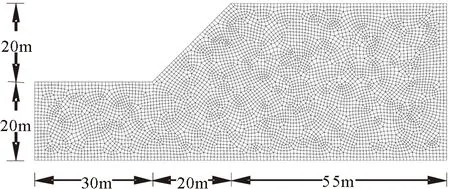
图3 计算网格图Fig.3 Discrete grid of the calculation model

从计算结果表2可见，利用基于ABAQUS二次开发平台实现的基于场变量的有限元强度折减法，采用塑性区贯通与坡脚点水平位移出现拐点作为有限元强度折减法判别边坡失稳的判据，综合确定的边坡安全系数为1.210，此安全系数与传统的有限元强度折减法计算结果完全一致，并且对应安全系数位于极限平衡M-P法和有限元极限平衡法之间，同时三者安全系数之间的绝对误差最大值为0.6%，这说明本文基于ABAQUS二次开发平台实现的基于场变量的有限元强度折减法对于均质边坡是有效的。

表2 安全系数汇总表

从图4中基于最大等效塑性应变搜索得到的滑动面位置与边坡失稳时刻的塑性区对比分析图可以看出，基于最大等效塑性应变搜索得到的滑动面位置位于等效塑性应变等值线密集的滑带范围内，并且可以清晰地看出塑性应变等值线的特征点刚好落在此滑动面上。

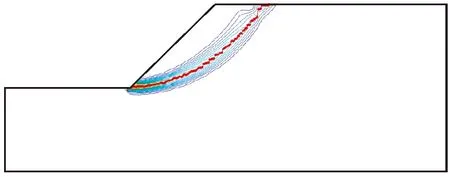
图4 基于最大等效塑性应变的边坡潜在滑动面确定Fig.4 Potential slip surface of the slope is determined by the maximum equivalent plastic strain

从图5中不同方案确定的边坡潜在滑动面位置可以看出，离散数据点组成的滑动面经过光滑处理后与滑动面雏形相近。极限平衡M-P法确定的边坡滑动面位置与基于最大等效塑性应变寻找方法确定的滑动面位置在下半段非常接近，但是在上半段本文方法相对于极限平衡法要深缓，但整体偏差较小。综上所述可说明基于最大等效塑性应变的搜索对均质边坡临界滑动面的精细化寻找是有效的。

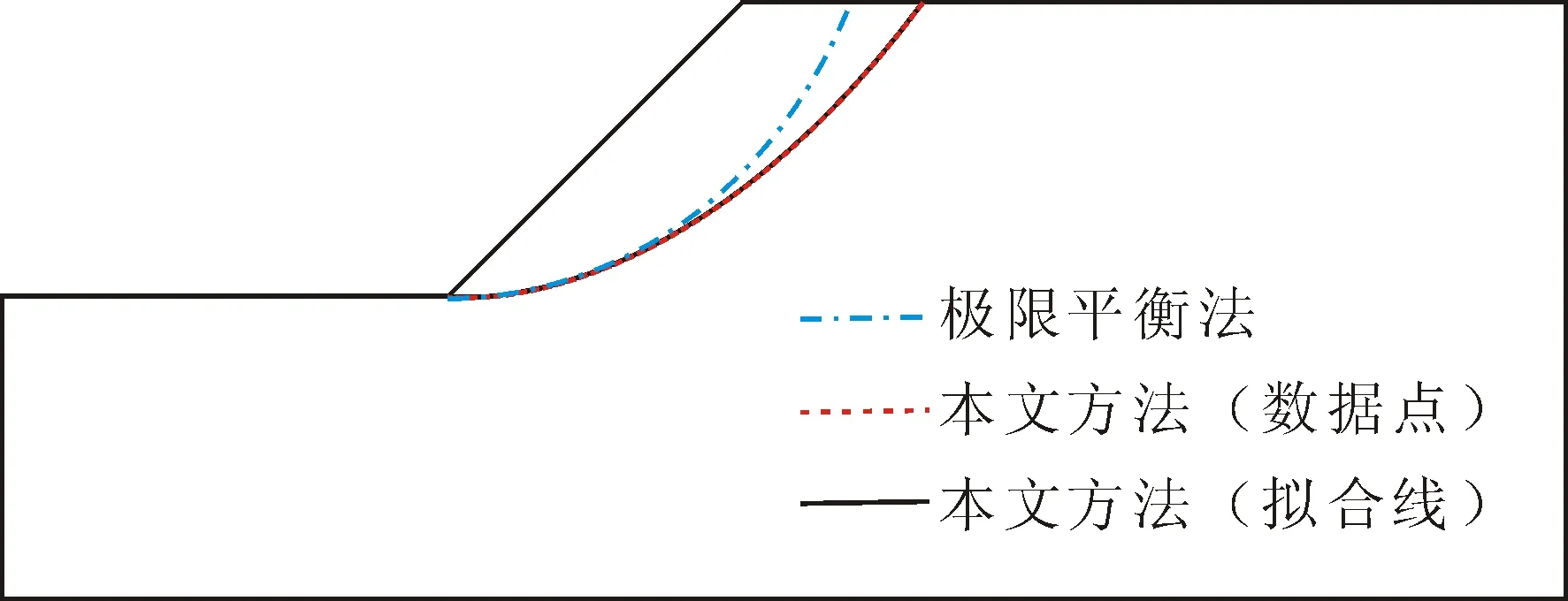
图5 不同方案确定的边坡潜在滑动面位置Fig.5 Positions of the potential slip surface of the slope are determined using the different schemes

3.2 非均质边坡算例分析

如图6所示,非均质边坡取自澳大利亚计算机应用协会(ACADS)的考核题[22]，为了在有限元计算中减小边界效应对计算结果的影响，将左侧边界延伸10m，向下延伸10m。具体模型尺寸为：坡高10m，坡比1 ∶2，模型总高度为25m，总宽度为60m；有限元计算模型共离散为16 556个单元，16 824个节点；模型两侧采用水平向约束边界，模型底部采用全约束边界。计算采用考虑Mohr-Coulomb强度准则的理想弹塑性模型,具体计算过程中所采用的材料参数见表3。

图6 计算网格图Fig.6 Discrete grid of the calculation model

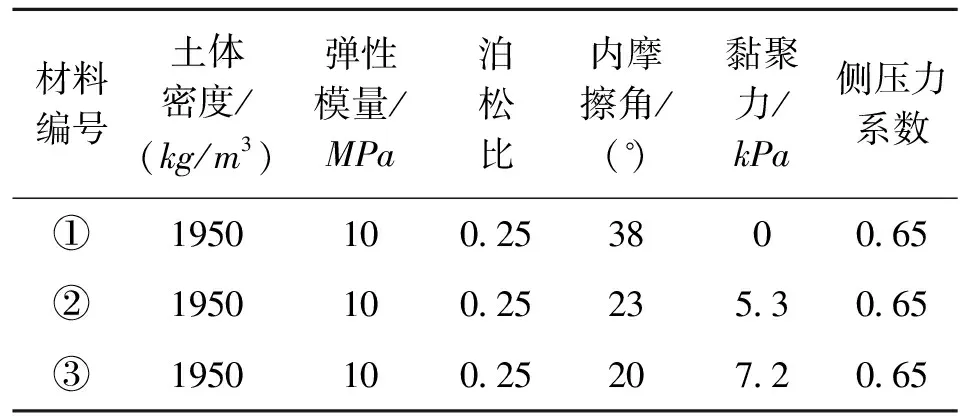
材料编号土体密度/(kg/m3)弹性模量/MPa泊松比内摩擦角/()黏聚力/kPa侧压力系数①195010025380065②1950100252353065③1950100252072065

从安全系数计算结果汇总表4可以看出，利用本文方法采用塑性区贯通与坡脚点水平位移出现拐点作为有限元强度折减法判别边坡失稳的判据，综合确定的边坡安全系数为1.364，此安全系数位于前人采用传统的有限元强度折减法确定的安全系数之间[21,23]，并且多种方法计算所得安全系数之间的彼此差别不大，这说明本文基于ABAQUS二次开发平台实现的基于场变量的有限元强度折减法在确定非均质边坡对应安全系数时也是适用的。

表4 安全系数汇总表

从图7中基于最大等效塑性应变搜索得到的滑动面位置与边坡失稳时刻的塑性区对比分析图可以看出，基于最大等效塑性应变搜索得到的滑动面位置位于边坡失稳时刻的塑性区内部，并且基于最大等效塑性应变搜索得到的滑动面基本上通过了等效塑性应变等值线的特征点。

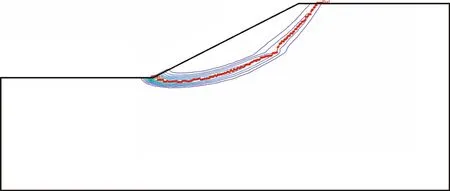
图7 基于最大等效塑性应变的边坡潜在滑动面确定Fig.7 Potential slip surface of the slope is determined by the maximum equivalent plastic strain

从图8中不同方案确定的边坡潜在滑动面位置可以看出，用极限平衡M-P法确定的边坡滑动面位置与基于最大等效塑性应变寻找方法确定的滑动面位置在滑动面下半段几乎重合，但在滑动面上半部分有一定的偏差。从本文方法的离散数据点明显可以看出塑性区在材料边界处的方向调整，然而基于极限平衡M-P法确定的边坡滑动面位置和本文方法拟合曲线均将此信息淹没。

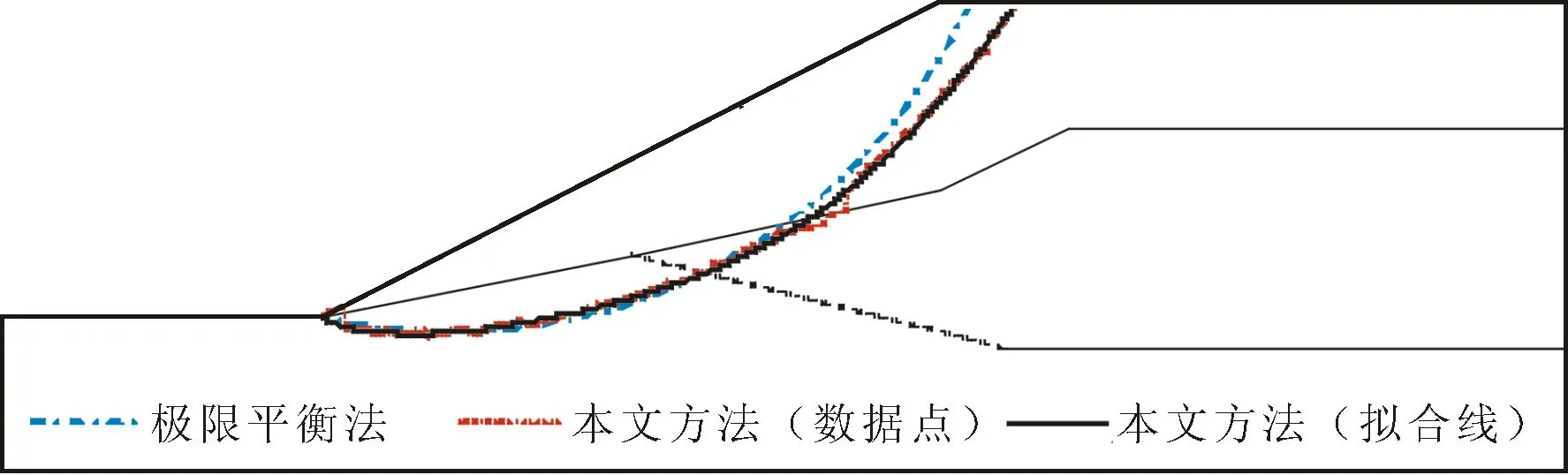
图8 不同方案确定的边坡潜在滑动面位置Fig.8 Positions of the potential slip surface of the slope are determined using the different schemes

但综合对比分析，两种方案的计算成果，可以发现两种方法确定的边坡潜在滑动面位置仍然在计算可接受的范围内，说明基于最大等效塑性应变的边坡滑动面精细化寻找方法对于非均质边坡是有效的。

4 结 论

1) 借助ABAQUS软件的二次开发平台的UFIELD程序，将软件自带的场变量定义为折减系数，建立场变量分别与软件求解时步和强度参数之间的关系，方便地实现基于场变量的边坡有限元强度折减法。此方法相对于其它方法的优势在于：仅需一次提交计算分析便可高效地实现边坡安全系数的求解。

2) 在基于场变量的边坡有限元强度折减方法计算所得等效塑性应变的基础上，利用不同垂直剖面逐点搜索法，实现了基于最大等效塑性应变的边坡潜在滑动面位置精细化寻找。

3) 通过两个经典算例，展示了此方法和思路进行边坡稳定性分析的效果，同时将此思路确定的潜在滑动面位置、安全系数分别与传统极限平衡M-P法的对应结果进行对比分析，发现不同方法确定的安全系数相差不大，两种方法确定的滑动面位置下半段相近，上半段本文方法确定滑动面相对于M-P法确定滑动面要深缓，但是两种方法的偏差较小，这说明本文所提方法是有效的。

[1]ZIENKIEWICZ O C, HUMPHESON C, LEWIS R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics [J]. Geotechnique, 1975, 25(4):671-689.

[2]唐芬, 郑颖人, 赵尚毅. 土坡渐进破坏的双安全系数讨论[J].岩石力学与工程学报, 2007, 26(7):1402-1407.

TANG Fen, ZHENG Yingren, ZHAO Shangyi. Discussion on two safety factors for progressive failure of soil slope[J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(7):1402-1407.

[3]YUAN Wei, BAI Bing, LI Xiaochun, et al. A strength reduction method based on double reduction parameters and its application[J].Journal of Central South University, 2013, 20(9):2555-2562.

[4]薛海斌, 党发宁, 尹小涛, 等. 边坡强度参数非等比例相关联折减法研究[J].岩石力学与工程学报, 2015, 34(S2):4005-4012.

XUE Haibin, DANG Faning, YIN Xiaotao, et al. Research on method of slope strength parameters non-proportional associated reduction[J].Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S2): 4005-4012.

[5]杨光华, 钟志辉, 张玉成, 等. 用局部强度折减法进行边坡稳定性分析[J].岩土力学, 2010, 31(S2):53-58.

YANG Guanghua, ZHONG Zhihui, ZHANGYucheng, et al. Slope stability analysis by local strength reduction method[J].Rock and Soil Mechanics, 2010, 31(S2):53-58.

[6]薛雷, 孙强, 秦四清, 等. 非均质边坡强度折减法折减范围研究[J].岩土工程学报, 2011, 33(2):275-280.

XUE Lei, SUN Qiang, QIN Siqing, et al. Scope of strength reduction for inhomogeneous slopes[J].Chinese Journal of Geotechnical Engineering, 2011, 33(2):275-280.

[7]陈国庆, 黄润秋, 周辉, 等. 边坡渐进破坏的动态强度折减法研究[J].岩土力学, 2013, 34(4):1140-1146.

CHEN Guoqing, HUANG Runqiu, ZHOU Hui, et al. Research on progressive failure for slope using dynamic strength reduction method[J].Rock and Soil Mechanics, 2013, 34(4):1140-1146.

[8]张鲁渝, 郑颖人, 赵尚毅, 等. 有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报, 2003, (1):21-27.

ZHANG Luyu, ZHENG Yingren, ZHAO Shangyi, et al. The feasibility study of strength reduction method with FEM for calculating safety factors of soil slope stability[J]. Journal of Hydraulic Engineering, 2003, (1):21-27.

[9]郑宏, 李春光, 李焯芬, 等. 求解安全系数的有限元法[J]. 岩土工程学报, 2002, 24(5):626-628.

ZHENG Hong, LI Chunguang, LEE C F, et al. Finite element method for solving the factor of safety[J].Chinese Journal of Geotechnical Engineering, 2002, 24(5):626-628.

[10]张培文, 陈祖煜. 剪胀角对求解边坡稳定的安全系数的影响[J].岩土力学, 2004, 25(11):1757-1760.

ZHANG Peiwen，CHEN Zuyu. Finite element method for solving safety factor of slope stability[J].Rock and Soil Mechanics, 2004, 25(11):1757-1760.

[11]杨光华, 张玉成, 张有祥. 变模量弹塑性强度折减法及其在边坡稳定分析中的应用[J]. 岩石力学与工程学报, 2009, 28(7):1506-1512.

YANG Guanghua, ZHANG Yucheng, ZHANG Youxiang. Variable modulus elastoplastic strength reduction method and its application to slope stability analysis[J].Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7):1506-1512.

[12]宋二祥. 土工结构安全系数的有限元计算[J].岩土工程学报, 1997, 19(2):1-7.

SONG Erxiang. Finite element analysis of safety factor for soil structures[J].Chinese Journal of Geotechnical Engineering, 1997, 19(2):1-7.

[13]GRIFFITHS D V, LANE P A. Slope stability analysis by finite element[J].Geotechnique, 1999, 49(3):387-403.

[14]连镇营, 韩国城, 孔宪京. 强度折减有限元法研究开挖边坡的稳定性[J].岩土工程学报, 2001, 23(4):407-411.

LIAN Zhenying，HAN Guocheng，KONG Xianjing. Stability analysis of excavation by strength reduction FEM [J].Chinese Journal of Geotechnical Engineering, 2001, 23(4):407-411.

[15]曹先锋, 徐千军. 边坡稳定分析的温控参数折减有限元法[J]. 岩土工程学报, 2006, 28(11):2039-2042.

CAO Xianfeng, XU Qianjun. Temperature driving strength reduction method for slope stability analysis [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(11):2039-2042.

[16]李宁, 许建聪. 基于场变量的边坡稳定分析有限元强度折减法[J]. 岩土力学, 2012, 33(1):314-318.

LI Ning, XU Jiancong. Strength reduction FEM for slope stability analysis based on field variable [J]. Rock and Soil Mechanics, 2012, 33(1):314-318.

[17]孙冠华, 郑宏, 李春光. 基于等效塑性应变的边坡滑面搜索[J]. 岩土力学, 2008, 29(5):1159-1163.

SUN Guanhua, ZHENG Hong, LI Chunguang. Searching critical slip surface of slopes based on equivalent plastic strain [J]. Rock and Soil Mechanics, 2008, 29(5):1159-1163.

[18]李剑, 陈善雄, 余飞. 基于最大剪应变增量的边坡潜在滑动面搜索[J]. 岩土力学, 2013, 34(supp.1):371-378.

LI Jian, CHEN Shanxiong, YU Fei. A method for searching potential failure surface of slope based on maximum shear strain increment [J]. Rock and Soil Mechanics, 2013, 34(supp.1):371-378.

[19]张媛, 李荣建, 李锦, 等. 超载作用下土质边坡失稳与破坏模式分析[J]. 西安理工大学学报, 2015, 31(3): 347-352.

ZHANG Yuan, LI Rongjian, LI Jin, et al. An analysis of instability and failure mode of soil slope under overloading action [J]. Journal of Xi’an University of Technology, 2015, 31(3): 347-352.

[20]MORGENSTERN N R, PRICE V E. The analysis of the stability of general slip surfaces [J]. Geotechnique, 1965, 15(1):79-93.

[21]邵龙潭, 李红军. 土工结构稳定分析—有限元极限平衡法及其应用[M]. 北京: 科学出版社, 2011.

[22]陈祖煜. 土质边坡稳定性分析—原理.方法.程序[M]. 北京: 中国水利水电出版社, 2003.

[23]杨有成. 强度折减法在斜坡稳定性分析中的适用性分析[D]. 武汉: 中国地质大学, 2008.

YANG Youcheng. Research on applicability of shear strength reduction method in slope stability analysis [D]. Wuhan: China University of Geosciences, 2008.

(责任编辑 杨小丽)

Research on the strength reduction FEM of the slope by applying the secondary development platform of ABAQUS

HOU Ling1， XUE Haibin2， ZHOU Zehua2， LIU Haiwei2， PAN Feng2

(1.School of Sciences，Xi’an University of Technology，Xi’an 710054，China；2.Institute of Geotechnical Engineering，Xi’an University of Technology，Xi’an 710048，China)

The strength reduction FEM plays an important role in the slope stability analysis. But the strength reduction FEM often gets the safety factor of slope by the dichotomy, which is less efficient because of its need for trial. With the secondary development platform UFIELD program of ABAQUS, the strength reduction FEM based on the field variable is realized by defining the field variable of the software as the reduction factor and establishing the relationship between the time step and strength parameters and field variable. This method only submits an analysis to calculate the safety factor of the slope effectively. Based on the principle that the equivalent plastic strain of the sliding zone is maximum, the searching for the location of the potential slip surface of the slope is realized using point by point searching method of different vertical profiles. Finally, taking the two typical slope as examples, the comparative analysis of the potential slip surface and safety factor is made by the traditional limit equilibrium method of M-P and the method proposed in this paper. Thus, the validity of the method proposed in this paper is verified.

strength reduction FEM of the slope；field variable；maximum equivalent plastic strain；potential slip surface

10.19322/j.cnki.issn.1006-4710.2016.04.013

2016-02-16

国家自然科学基金资助项目(51679199)；水利部公益性行业科研专项基金资助项目(201501034-04);陕西省科技统筹创新工程重点实验室资助项目(2014SZS15-Z01)

候玲，女，副教授，研究方向为计算力学。E-mail：houling@xaut.edu.cn

TU43

A

1006-4710(2016)04-0449-06