预期寿命与国民储蓄率：基于可变增长率系数总储蓄方程的分析

金 刚,张秋秋

(1.辽宁大学 人口研究所,辽宁 沈阳 110036; 2.沈阳大学 工商管理学院,辽宁 沈阳 110044)



预期寿命与国民储蓄率：基于可变增长率系数总储蓄方程的分析

金 刚1,张秋秋2

(1.辽宁大学 人口研究所,辽宁 沈阳 110036; 2.沈阳大学 工商管理学院,辽宁 沈阳 110044)

本文放松传统生命周期假说关于个体寿命与工作期时长固定不变的假设，将一般形式的生存函数加入生命周期理论分析框架。与传统生命周期假说总储蓄方程中经济增长率系数为常数的结论不同，研究发现加入生命函数的总储蓄方程中经济增长率的系数是可变的，15岁开始的预期寿命延长会显著提高经济增长率的系数，而15-60岁工作期预期寿命延长会显著降低经济增长率的系数，利用全球218个国家1981-2010年面板数据的实证结果较好地支持了前述结论。随着预期寿命的延长，总储蓄方程中经济增长率系数有提高的趋势，但包括中国、韩国在内的部分国家(地区)的经济增长率系数提高幅度较大，这可能是这类国家(地区)国民储蓄率的变动率明显高于经济增长率的变动率的原因。

预期寿命；工作期；经济增长率；国民储蓄率；可变增长率系数；总储蓄方程

一、引 言

改革开放以来中国经济保持着较快增速，伴随着快速经济增长，中国的国民储蓄率水平也出现了明显的提高，1980年中国国民储蓄率为34.5%，2010年最高达到50.9%，2014年略微下降至48.8%①① 中国国家统计局网站。，按照世界银行数据，2013年中国的储蓄率水平在全球排名第五②② 世界银行数据库。。许多学者基于不同理论对中国高储蓄现象进行了解释，其中，生命周期理论是具有代表性的主流观点之一。传统生命周期理论的核心结论是在经济和人口均衡时，总储蓄率与经济增长率具有近似的线性关系，因此快速的经济增长可能是引致中国国民储蓄率提高的主要原因。按照生命周期理论的基本结论，总储蓄率的变化率与经济增长率的变化率应该近似相等，美国和中国香港等国家和地区国民储蓄率与经济增长率的明显同步特征基本印证了生命周期理论，但是，中国的现实情况却与生命周期理论结论存在着一定的偏离，1981-2010年间，中国的国民储蓄率的变化率明显快于经济增长率的变化率，也有其他的国家(地区)同样显示出了与中国类似的现象。图1列出了1981-2010年中国、韩国、美国和中国香港的国民储蓄率和GDP增长率的变动情况。

图1显示，1981-2010年美国和中国香港的国民储蓄率与GDP增长率表现出较为明显的同步特征，而相同时间段内，中国与韩国的情况却有所不同。1981-2010年，中国经济增长率相对稳定，而国民储蓄率却表现出明显的上升趋势，特别是在2001-2005年之后，中国GDP增长率小幅下降后略有上升，但国民储蓄率却表现为相对平稳之后的快速上升；韩国在1986-1990年之后经济增长率呈现下降趋势，而国民储蓄率却表现得比较平稳。分析其原因，我们认为有可能是中国以及韩国的经济增长率对国民储蓄率的边际贡献发生明显的提高，从而引起国民储蓄率增幅高于GDP增长率的增幅。

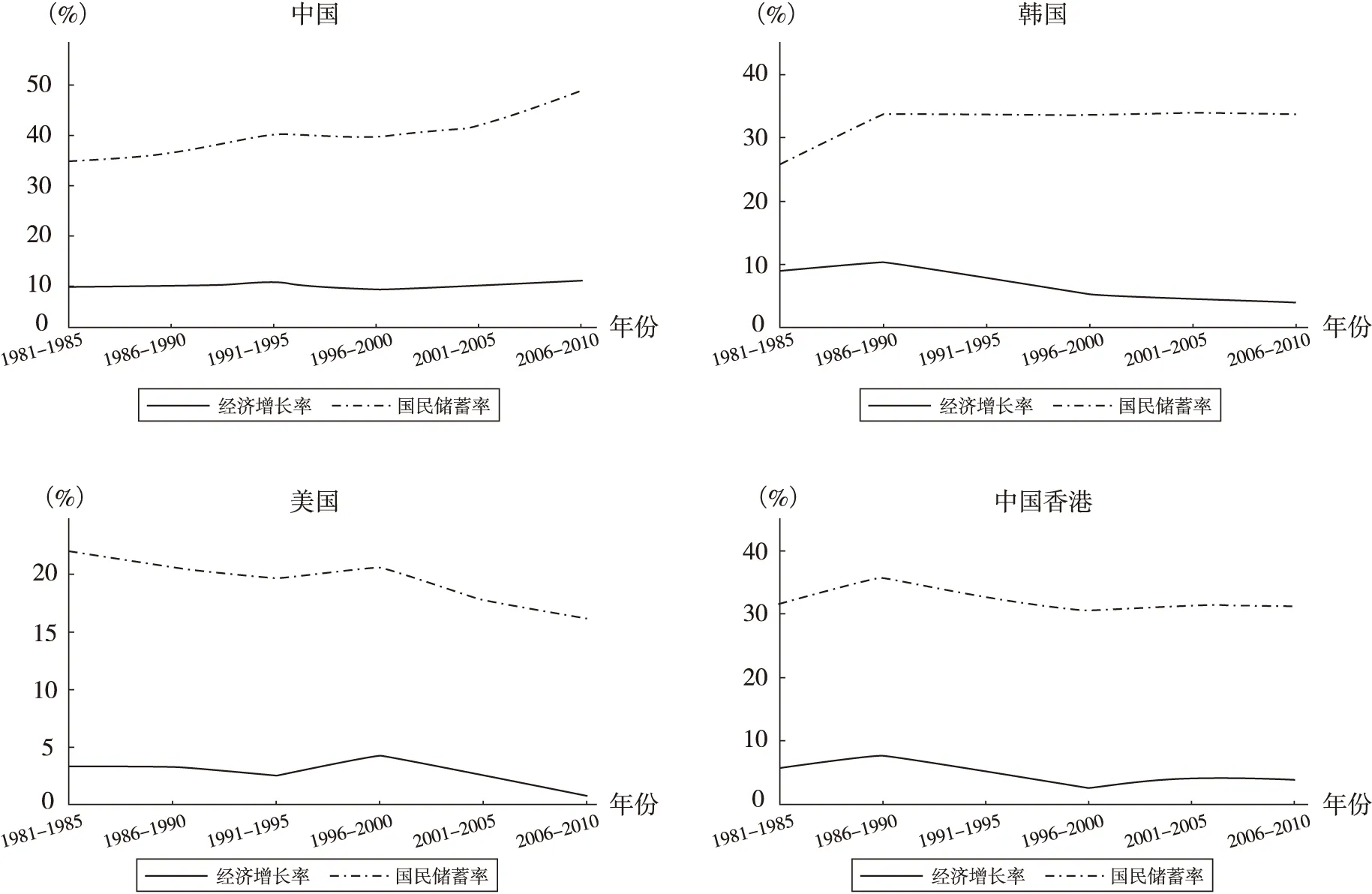
图1 四国(地区)的经济增长率与国民储蓄率

按照传统生命周期假说的观点，总储蓄率方程中经济增长率的系数是由不同年龄个体未来寿命和未来工作期时长的函数所决定的，由于将生命时长和工作期时长均设定为常数，因此总储蓄率方程中经济增长率的系数为常数[1]。但是，现实条件下寿命和工作期时长都是数学期望值，会随着生存概率的变化而发生变化，因此经济增长率的系数也可能会随之发生变化。预期寿命的变化本质上是生存概率变动的结果，传统生命周期假说并未对生存概率以及预期寿命的影响进行分析，而目前针对预期寿命储蓄效应的研究基本采取直接将预期寿命加入总储蓄率方程的方法，从而可能忽略生存概率变动所引致的预期寿命变动对经济增长率边际储蓄效应的影响。基于上述分析，本文尝试将生存概率引入生命周期分析框架，在生存概率可变的条件下，通过个体消费加总来研究总储蓄率的决定机制。研究发现预期寿命和工作期预期寿命与经济增长率对国民储蓄率具有交互影响，预期寿命与工作期预期寿命的变动会影响总储蓄率方程中经济增长率的系数，预期寿命的延长会提高经济增长率的边际储蓄效应，工作期预期寿命的延长则会降低经济增长率的边际储蓄效应。利用1981-2010年跨国面板数据的实证检验结果较好地支持了本文的理论分析结论。

本文共为五个部分，第二部分为文献回顾，第三部分为加入生存概率后总储蓄率决定的理论分析，第四部分利用1981-2010年跨国面板数据对理论分析结论进行实证检验，第五部分总结研究发现。

二、文献回顾

Modigliani[1-2]等提出的生命周期假说，打破了凯恩斯绝对收入假说关于现期收入决定现期消费的研究视角，转而重新回归到消费者行为的基础理论。该假说最具颠覆性的观点是，消费者将建立实现一生效用最大化的消费储蓄计划安排，而某一时期的消费率仅是消费者一生计划安排的一个方面。生命周期假说建立在消费者选择理论基础之上，并假设消费者效用由当期和未来各期消费共同决定，消费者各期可利用的资源是现期收入、未来收入折现值以及现期净财富的总和，消费者将在此预算约束下通过各期消费的安排实现一生效用最大化，效用最大化的当期消费将是其可利用的资源、资本回报率以及年龄和未来寿命的函数。在个体消费决定基础上，在预期寿命、利率、人口增长率等其它参数不变的假设下，通过对所有个体消费加总除以总收入所得到的总储蓄率将是经济增长率的函数，进一步对经济增长率进行一阶泰勒级数展开，生命周期假说得出的主要结论是，在人口与经济均衡时，总储蓄率与经济增长率具有s≈α+β·g的线性关系，其中，s为总储蓄率，g为经济增长率。

传统生命周期假说的核心假设之一是个体寿命与工作时长固定不变，由于寿命和工作时长是生命周期假说总储蓄率方程中经济增长率系数的决定因素，因此在该假设下经济增长率的系数近似为常数。然而，现实中的预期寿命是不断变化的，1950年以来全球预期寿命显示出明显的上升趋势，1950-1955年全球出生时预期寿命仅为46.91岁，2010-2015年全球平均出生时预期寿命已经提高至70岁。预期寿命延长对储蓄率的影响逐步引起了国内外学者的关注，Deaton[3-4]、Hurd[5]、刘生龙[6]等的研究发现出生时预期寿命的延长会显著提高个体或家庭的储蓄率，Lee[7-8]、范叙春[9]等研究发现出生时预期寿命延长会显著提高总储蓄率水平，金刚[10]等研究发现15-60岁工作期预期寿命的提高会显著降低国民储蓄率水平，60岁开始的老年期预期寿命的延长则会显著提高国民储蓄率水平。上述研究以实证方法为主，基本都采取了将预期寿命直接加入总储蓄方程进行计量检验的方法，对于预期寿命变动影响个人储蓄以及加总储蓄的理论分析尚显不足。Bloom[11]将生存概率引入生命周期理论分析框架，分析了预期寿命延长条件下的个体消费决策以及加总储蓄决定，研究发现即使在自由选择退休年龄条件下，预期寿命的延长依然具有显著提高个体储蓄率和总储蓄率水平的效应。尽管该研究进一步推进了预期寿命储蓄效应的理论分析，但也未关注预期寿命对总储蓄率方程中经济增长率系数的影响。同时，该研究将生存函数设定为指数分布的形式，由于指数形式的生存函数意味着个人在一生之中任何时间具有相同的死亡力，因此只适用于短期分析，而不适用于个人生命跨度长达几十年的中长期分析。

相较于之前的研究，本文的改善主要体现在：(1)使用一般形式的生存函数替换目前研究中使用的指数分布生存函数，通过将一般形式生存函数加入生命周期理论研究框架，分析个体消费决策以及个体消费加总形成的总储蓄决定机制；(2)引入分段预期寿命概念，分析15岁开始的预期寿命和15-60岁工作期预期寿命分别与经济增长率的交互项对国民储蓄率的影响效应，进而提出可变增长率系数总储蓄率方程；(3)利用全球218个国家30年的面板数据，并通过每5年期取各变量平均值来克服短期经济波动及测量误差，对可变增长率系数总储蓄方程进行实证检验。

三、理论分析

(一)个体消费

假设个体从出生开始生存至a岁的概率为sa(0)，ca为个体a岁时的消费，效用函数为对数形式U(ca)=ln(ca)，加入生存概率后，个体一生效用最大化问题可表示为：

(1)

其中，ρ≥0为时间偏好，ω为最高寿命。个体在任意时点面临的预算约束为：

(2)

(3)

个体在任意年龄a岁的消费将为ca=co·e(r-ρ)a。假设个体无遗产动机，个体会实现一生消费精算现值与一生收入精算现值相等，初始消费占初始收入的比例将为：

(4)

其中，w0为个体在初始期的收入，σ为人均收入增长率，R为退休年龄。式(4)说明，为了实现一生的效用最大化，个体将在初始期选择收入的一定比例进行消费，而这个比例独立于当期收入。

(二)加总储蓄率的决定

假设人口均衡增长率为n，经济增长率将为g=σ+n。时刻T的总消费可以表示为各个年龄所有人消费的加总：

(5)

(6)

为了简化分析，假设r=ρ=0，将初始消费比重式(4)代入式(6)，分别对eσa、e-ga和e-na在σ=g=n=0处进行一阶泰勒级数展开，并左右两边取对数，利用ln(1+x)≈x，总储蓄率方程可整理为：

+εT

(7)

(三)加入预期寿命的可变增长系数总储蓄率

方程

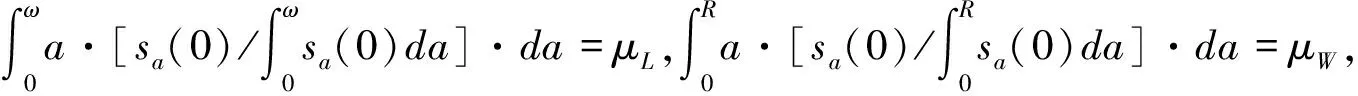
sT=α0+g·(μL-μW)+εT

(8)

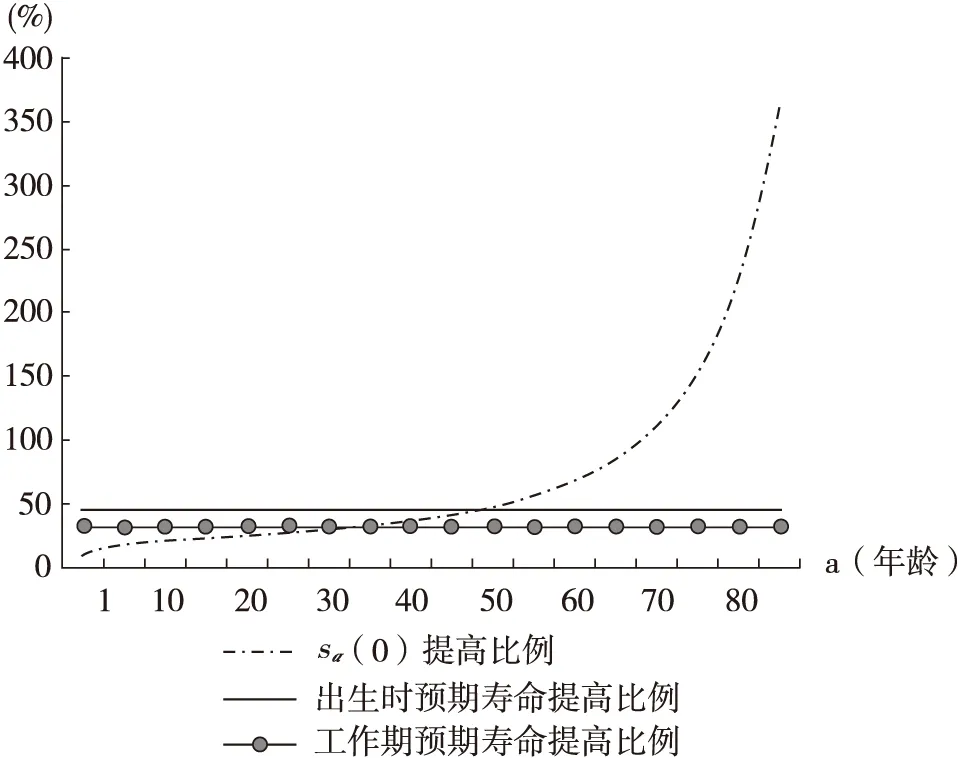
图2 1950-2010年预期寿命与生存概率的提高比例

数据来源：联合国人口司数据库。

图2显示，从出生开始生存至a岁的概率sa(0)的提高比例明显表现出递增的趋势，大约在45岁之前，sa(0)的提高比例小于出生时预期寿命的提高比例，而大约在45岁之后，sa(0)的提高比例高于出生时预期寿命的提高比例；工作期分段预期寿命提高比例与sa(0)提高比例的对比也显示出基本一致的特征。

(9)

(10)

其中，z0-ω为出生时预期寿命，z0-R为工作期预期寿命。将式(9)、(10)带入总储蓄率方程式(8)，总储蓄率方程可进一步表示为：

sT=α0+γ0·g+γ1·z0-ω·g-γ2·z0-R·g

(11)

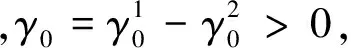
四、实证检验

(一)计量方程

由于个体不可能在出生时即开始工作，因此总储蓄率方程式(11)中包含的预期寿命变量z0-R与z0-ω应该从工作期开始。然而，工作期的开始年龄和退休期的开始年龄在实证研究中获得精确测定比较困难，原因是多方面的。首先，个体平均教育年限不断增加，这意味着工作期开始年龄随着预期寿命延长在不断提高；其次，尽管目前世界上大多数国家都建立了养老保险制度并规定了退休年龄，但是退休年龄规定并不完全是强制性的，并且不同国家养老保险制度的退休激励效应不同，因此提前退休和延迟退休在不同国家中都一定程度的存在；再次，部分国家的养老保险制度并不是全覆盖的，部分人群可能依然处于养老保险制度覆盖范围之外。基于此，本文考虑利用劳动力年龄组划分标准来构建z0-ω与z0-R的代理变量来对式(11)进行检验。对劳动力的年龄界定一般从15岁开始，因此我们假设15岁为工作期开始年龄，对老年人口的年龄界定有60和65岁两种方法，我们将60岁设定为退休期开始年龄预期寿命与生存概率相关数据从联合国人口司数据库获得，原始数据即为1980-1985，1985-1990，1990-1995，1995-2000，2000-200。在前述设定下有：

z0-ω=e15

(12)

z0-R=e15-45p15·e60

(13)

其中，e15为从15岁开始的预期寿命，e60为从60岁开始的预期寿命，45p15为15岁个体存活至60岁的概率。我们分析的是均衡状态下总储蓄率的决定，由于指标短期波动会对总储蓄率产生影响，因此我们采用Kraay[12]的方法对各个指标每五年取平均值以降低指标短期波动程度，这种处理方法也有利于降低各指标的测量误差。同时，由于消费习惯等原因，人们面对约束条件的变化时，消费水平不可能立刻转变，总储蓄率的变动也不可能即刻完成，这意味着不同均衡状态之间的转换需要一定的时间。因此，我们参照Bloom[11]等的方法，将储蓄率的滞后项加入计量方程。根据已有的研究结果，人口抚养比以及出生时预期寿命可能对总储蓄率水平具有影响，因此我们在储蓄率方程中进一步加入了人口结构变量和出生时预期寿命。计量方程确定为：

sT=α0+β0·g+β1·z0-ω·g+β2·z0-R·g+β3·sT-1+∑βi·Xi+εT

(14)

其中，g为经济增长率，z0-ω为15岁开始的预期寿命，z0-R为15至60岁的工作期分段预期寿命，sT-1为滞后一期的储蓄率，Xi为少儿人口比重(youthratio)、老年人口比重(oldratio)和出生时预期寿命(e0)。根据理论分析结果，我们预期β0>0，β1>0，β2<0。

(二)数据处理及描述性统计

我们搜集了包括中国在内的全球218个国家的储蓄率、经济增长率、预期寿命等指标从1981至2010年共30年的数据，并对所搜集的数据按照每五年一个时间段计算平均值。本文使用的储蓄率为国内总储蓄占国内生产总值的比重，经济增长率为按照相同价格测算的年增长率。少儿人口比重为0-14岁人口比例，老年人口比重为65岁及以上人口比重。对各变量每五年取平均值之后①① 预期寿命与生存概率相关数据从联合国人口司数据库获得，原始数据即为1980-1985，1985-1990，1990-1995，1995-2000，2000-2005，2005-2010各时间段的取值；其他变量我们从1981年开始每5年取平均值，即为1981-1985，1986-1990，1991-1995，1996-2000，2001-2005，2006-2010年的平均值。，所有变量描述性统计情况见表1。

表1 变量的描述性统计

注：预期寿命与生存概率数据来自联合国人口司数据库，其他数据来自世界银行数据库。

(三)估计结果

我们首先使用固定效应方法对理论分析结论进行检验，估计结果见表2。模型(1)的自变量仅包含经济增长率，经济增长率的系数显著为正，与生命周期假说的基本结论一致。在模型(1)的基础上，模型(2)加入了本文主要关注的经济增长率与预期寿命相关变量的两个交互项，估计结果显示，z0-ω·g的系数显著为正，z0-R·g的系数显著为负，与理论分析结论一致。模型(3)进一步加入了滞后一期的储蓄率。模型(4)增加了人口结构变量，模型(5)增加了出生时预期寿命，估计结果也与之前模型的估计结果基本一致。从固定效应方法估计结果来看，经济增长率的系数显著为正，经济增长率与15岁开始的预期寿命的交互项z0-ω·g的系数显著为正，经济增长率与15-60岁工作期分段预期寿命的交互项z0-R·g的系数显著为负，这一结果较好地支持了本文的理论分析结论。

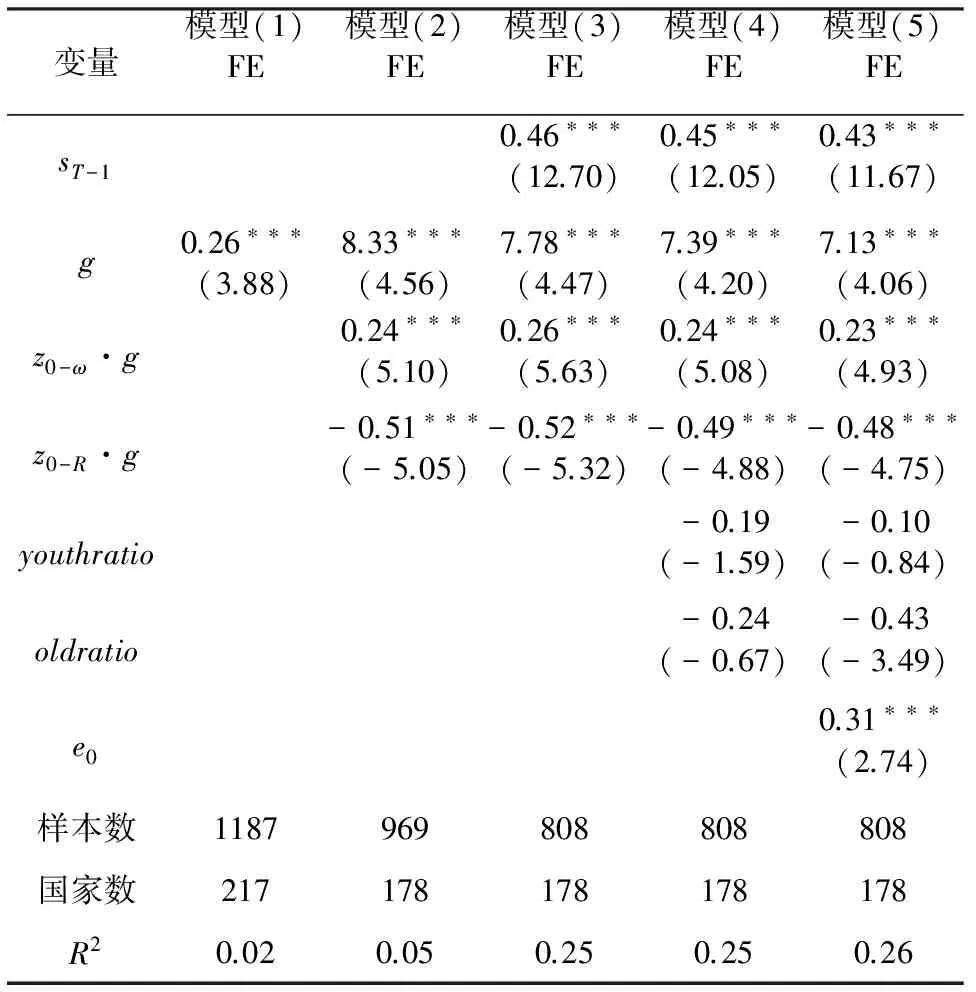
表2 固定效应方法估计结果

注：利用stata 14.0进行估计；省略常数项结果；*、**、***分别表示在10%、5%、1%水平上显著；括号内为t值。下同。

动态面板数据条件下，滞后因变量与误差项相关，同时，总储蓄率方程中的误差项可能与经济增长率相关。为了解决内生性造成的估计结果偏误，本文进一步利用动态面板估计方法对总储蓄率方程进行检验。同时，为了提高模型的稳健性，我们根据世界银行对不同国家(地区)按照收入水平的分组方法，将总体样本分为高收入组和低收入组进行分组动态面板估计。动态面板方法的估计结果见表3。

表3 动态面板方法估计结果

注：时间虚拟变量作为外生变量，将滞后一期的储蓄率以及模型中的其他自变量作为内生变量，滞后期设定为5期。

模型(6)为总体样本的系统GMM估计，模型(7)为总体样本的差分GMM估计，从估计结果来看，滞后一期储蓄率的系数显著为正，经济增长率与预期寿命交互项的系数显著为正，经济增长率与15岁开始的工作期预期寿命交互项的系数显著为负，估计结果与固定效应估计结果基本一致。模型(8)与模型(9)分别为高收入组样本的系统GMM估计和差分GMM估计，估计结果与总体样本基本一致。模型(10)与模型(11)为低收入组样本的系统GMM估计和差分GMM估计，估计结果也与其他模型一致。总体样本与分组样本动态面板估计结果也较好地支持本文的理论研究结论。值得注意的是，在加入生存概率之后，少儿人口比重、老年人口比重和出生时预期寿命的系数在动态面板估计中显著性都不高，人口因素对总储蓄率的影响主要体现在预期寿命和工作期预期寿命分别与经济增长率对国民储蓄率的交互影响，这也意味着较前研究中直接将出生时预期寿命加入计量方程进行检验的方法可能是值得商榷的。

根据本文的研究结果，生命周期假说的总储蓄率方程应该表示为式(11)，随着预期寿命的变动，经济增长率的系数将是可变的。按照Modigliani[1]的研究结论，在出生时预期寿命和工作期时长不变的情况下，总储蓄率方程中经济增长率的系数将是主要由出生时预期寿命和工作期时间长度的函数所决定的常数。但是，加入生存概率后，由于预期寿命和工作期预期寿命都是可变的，因此经济增长率的系数也将是可变的。本文的理论研究结论和实证估计结果都证明了预期寿命对经济增长率的国民储蓄边际效应大小具有影响。具体来看，15岁开始的预期寿命的延长会显著提高经济增长率的系数，而15-60岁工作期预期寿命的延长则会显著降低经济增长率的系数。

根据金刚[10]等的研究，全球平均15岁开始的预期寿命仍在普遍延长，而工作期预期寿命在部分国家特别是相对高收入国家(地区)已经呈现出稳定的趋势。同时，图2也显示出，出生时预期寿命的增长比例明显高于工作期预期寿命的增长比例。在这种预期寿命以及工作期预期寿命的变动趋势下，我们推测经济增长率的系数是逐步增大的。利用总体样本的系统GMM估计结果计算，中国1981-1985年经济增长率的系数约为0.24，2006-2010年经济增长率系数提高至0.69，经济增长率以及经济增长率系数的变动共使国民储蓄率增长了约5.44个百分点，占同期中国国民储蓄率增长的32.62%。表4列出了根据估计结果计算的1981-2010年美国、中国香港、中国和韩国的经济增长率对国民储蓄率边际影响效应的变动情况。

表4 1981-2010年根据实证分析结果计算的四国(地区)系数变动情况

注：根据模型(6)相关变量系数计算。

表4中数据显示，四国(地区)总储蓄方程中经济增长率系数都是逐步增大的，但是美国和中国香港经济增长率系数的增长明显要更平稳，相邻时间段经济增长率系数提高的幅度约为10%～20%，并且增幅有下降的趋势。中国与韩国的情况与美国和中国香港不同，中国经济增长率系数在2001-2005年之前小幅增长，但在2001-2005年增长幅度接近100%，从图1来看，这个时点与中国国民储蓄率增速从2005年开始明显快于GDP增速大致相吻合；韩国在1986-1990年经济增长率系数比前一时间段提高了一倍以上，相邻时间段经济增长率系数的增幅一直保持在接近50%的水平，明显高于美国和中国香港的增速。在实证检验中本文将退休年龄设定为60岁，考虑到预期寿命延长条件下劳动力实际退出劳动力市场的年龄可能会有一定程度的延后，这会引起工作期预期寿命的提高并进而一定程度上抵消经济增长系数的提高，因此美国和中国香港这类经济增长率系数变动幅度较低的国家和地区的实际经济增长率系数可能会比较稳定，从而使国民储蓄率与经济增长率表现为同步的变化，而中国与韩国这类经济增长率系数出现大幅度提高的国家，即使在去除其他因素的影响后，经济增长率系数可能也是明显提高的，因此表现为国民储蓄率的变动率高于GDP增长率的变动率，这可以在一定程度上解释图1显示出的国民储蓄率与GDP增长率变动的两类不同特征。

在一定的医疗、经济和社会发展等条件下，预期寿命不可能无限上升，工作期预期寿命也将趋于稳定，因此经济增长率系数提高的趋势不会一直延续，随着预期寿命的稳定，经济增长率的系数也会趋于平稳，这将与传统生命周期理论的基本结论相符。例如，表4中数据显示中国香港2001-2005年和2006-2010年的经济增长率系数增幅已经下降至10%以下，其原因是中国香港的预期寿命在全球排名第二，相对于预期寿命较低的国家和地区，中国香港预期寿命的增长速度开始相对放缓。从这个意义上说，传统生命周期理论将预期寿命与工作时长设定为常数的方法，适用于人类寿命达到极限之后的稳定状态，而在此之前，预期寿命主要呈现增长趋势，预期寿命的变动使经济增长对国民储蓄率的边际影响效应发生着变化。

五、研究结论与政策涵义

本文的主要研究结论是：(1)在生命周期理论分析框架中加入生存概率之后，预期寿命的变化会引起总储蓄率方程中经济增长率的系数发生变化，即经济增长率的系数是可变的。(2)15岁开始的预期寿命与15-60工作期预期寿命分别与经济增长率对国民储蓄率具有交互影响，15岁开始预期寿命的延长会增大总储蓄率方程中经济增长率的系数，而工作期预期寿命的延长则会使总储蓄率方程中经济增长率的系数减小。在经济增长率不变时，15岁开始预期寿命的延长将使国民储蓄率提高，而工作期预期寿命的延长将国民储蓄率水平降低。(3)随着预期寿命的延长，总储蓄率方程中经济增长率的系数有提高的趋势，部分国家和地区的经济增长率系数提高幅度较大，这可以在一定程度上解释中国、韩国等国家的国民储蓄率的变动率明显高于经济增长率的变动率的现象。按照本文的测算结果，1981-2010年间，经济增长率以及经济增长率系数的提高，使中国国民储蓄率增长了约5.44个百分点，占同期中国国民储蓄率增长的32.63%。

近期中国经济增长有小幅放缓的趋势，这在一定程度上会降低国民储蓄率水平，但由于预期寿命的延长，中国的经济增长率对国民储蓄率的边际影响效应可能将会进一步提高，经济增速放缓降低国民储蓄率的效果将会减小，如果以降低国民储蓄率和提高消费水平作为政策目标，在预期寿命延长的条件下，实施延迟退休制度以提高个人对工作期时长的预期，强化管理以有效解决提前退休问题，建立养老金计发激励机制以促进个体延长工作和缴费年限，完善劳动力市场为老年人口提供适当的就业机会和岗位等办法，可以成为有效的政策选择。

[1] Ando A, Modigliani F. The “life-cycle”hypothesis of saving: Aggregate implications and tests[J].American Economic Review, 1963, 53(1): 55-84.

[2] Modigliani F, BrumbergR. Utility analysis and the consumption function: An interpretation of cross-section data[A]. Kurihara K K. Post-Keynesian Economics[M].Rutgers University Press, 1954.388-436.

[3] Deaton A, Paxson C. Saving, growth, and aging in Taiwan[A].Studies in the Economics of Aging[C]. University of Chicago Press, 1994.331-362.

[4] Deaton A, Paxson C. Growth, demographic structure, and national saving in Taiwan[J]. Population and Development Review, 2000, 26(Supplement): 141-173.

[5] Hurd M D, McFadden D L,Gan Li. Subjective survival curves and life cycle behavior[A]. Inquiries in the Economics of Aging[M]. University of Chicago Press, 1998. 259-309.

[6] 刘生龙, 胡鞍钢, 郎晓娟. 预期寿命与中国家庭储蓄[J]. 经济研究, 2012(8):108-118.

[7] Lee R, Mason A, Miller T. Saving, wealth and the demographic transition in East Asia[R]. East-West Center Working Paper, Population Series No. 88-7,1997.

[8] Lee R, Mason A, Miller T. Life cycle saving and the demographic transition: the case of Taiwan[J]. Population and Development Review, 2000, 26(Supplement): 194-219.

[9] 范叙春,朱保华.预期寿命增长、年龄结构改变与我国国民储蓄率[J].人口研究, 2012(4):20-30.

[10] 金刚,柳清瑞, 张秋秋.分段预期寿命对国民储蓄率的影响效应[J]. 中国人口科学,2015(3):69-78.

[11] Bloom D E, Canning D, Mansfield R, Moore M. Demographic change, social security systems, and savings[J]. NBER Working Paper No.12621, 2006.

[12] Karry A. Household saving in China[J].The World Bank Economic Review, 2000, 14(3): 545-570.

责任编辑、校对：郑雅妮

2016-04-26

本文得到国家哲学社会科学基金青年项目“人口老龄化高峰期养老保险基金缺口应对研究”(12CRK010)和辽宁省教育厅优秀人才支持计划(WJQ2014003)的资助。

金刚(1976- )，辽宁省抚顺市人，经济学博士，辽宁大学人口研究所副研究员，研究方向：人口与社会保障；张秋秋(1978- )，女，辽宁省沈阳市人，经济学博士，沈阳大学工商管理学院副教授，研究方向：人力资源与社会保障。

A

1002-2848-2016(06)-0064-09