基于最小生成树的渠道系统优化布局模型
许自昌
(1. 中国地质大学(武汉)资源学院,武汉430074;2. 福建省地质测绘院遥感中心,福州 350011)
·农业水土工程·
基于最小生成树的渠道系统优化布局模型
许自昌
(1. 中国地质大学(武汉)资源学院,武汉430074;2. 福建省地质测绘院遥感中心,福州 350011)
针对平原地区农田灌溉渠道优化布局问题,当前普遍采用渠道布局原则进行布局,但其不能取得成本最优的布局。通过简化平原地区农田灌溉渠道优化布局问题,该文构建了基于最小生成树的渠道优化布局模型。与传统最小生成树模型不同的是该模型涵盖了2级渠道的优化布局问题,而且该模型得到的方案要大于等于1棵最小生成树。为了能利用成熟的最小生产树理论的求解方法,该文通过创建虚拟点概念去除渠道优化布局模型和传统最小生成树模型的区别,运用凸壳理论讨论求解该模型的 4种情况,编写求解该模型的LINGO程序,然后将基于最小生成树的渠道优化布局模型用于案例,得到了研究区渠道布局方案。该方案的工程量是16 095 m3,而采用渠道布局原则得到的渠道布局方案的工程量是16 938.25 m3。结果表明基于最小生成树的渠道优化布局模型能得到成本更少的渠道布局方案,即最大程度地控制土地整治费用。研究为控制土地整治项目的费用提供了一条有效途径。
渠道;优化系统;土地复垦;布局;最小生成树模型;凸壳理论;LINGO
0 引 言
现有的土地复垦工程研究主要集中在土方工程、GIS技术应用方面[1-6],现有研究成果能提供精确的定量模型,进行复垦工程的土方计算,但是关注沟渠布局的研究很少,特别是建立定量模型进行沟渠优化布局的研究更少[7-12]。沟渠工程费用占土地复垦工程费用比例较大,因此有必要进行相关研究,为沟渠优化布局提供依据,从而节约工程费用。在灌溉与排水工程设计规程和农田水利学等专业书籍或期刊里,有部分关于沟渠路的布局模式及布局原则的描述[12-18],也有一些简单的布局模型对农田的灌溉系统进行优化。仅依靠这样的定性说明进行布局,得不到成本最优的布局方案[19-22]。该文选择平原地区的采煤塌陷地作为研究区域,通过构建定量的数学模型,寻找成本最优的布局方案,以期为土地整理项目渠道优化布局提供依据。
1 沟渠优化布局总体思路
在平原地区,田地受地形条件限制较少,各田块比较规整,而且根据土地开发整理项目规划设计规范,划分田块的长边和短边都必须在一定范围内,不会相差很多,因此平原地区的田块近似于矩形,田块与田块的拓扑关系近似于图1。
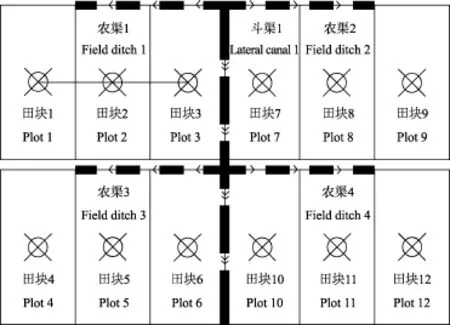
图1 土地整治灌溉渠道布局示意图Fig.1 Diagram of irrigation canals layout for land consolidation
图1中农渠1将田块1、2、3连接在一起,并负责这些田块的灌溉任务,其长度等于田块2、3的短边之和,由于各田块规格相同,即其长、宽均相等,因此满足田块1、2、3的灌溉渠道的长度等于3个田块重心之间的距离。以此类推,在一定范围内的农田布局渠道,可以简化为将该范围内的田块重心连接起来。因此,灌溉渠道优化布局问题可转化为网络优化问题。此处的网络是指运筹学中定义的网络,又称为图,是由一系列节点和一系列连接点的线组成。
渠道优化布局问题可以近似描述为寻找一系列重心点之间的1个弧集合,这些弧把所有的重心点连接起来,并且这些弧的长度之和最小[23-27]。这跟最小生成树的定义类似,所以土地整治渠道优化布局问题可以抽象为1个近似最小生成树问题。该模型与传统的最小生成树模型有以下区别:1)体现在渠道优化布局模型要解决的是2级渠道的最优化布局问题,并且这2级渠道的成本是不一样的,但是最小生成树模型中连接节点的弧具有单位长度同质的前提假设,也就是说,如果用现有的最小生成树模型处理渠道最优化布局问题只能解决 1 级渠道的最优化布局问题。因此,很多文献中的解决方法是先按一定原则确定上一级渠道的走向,然后再运用最小生成树模型确定下一级渠道的最优布局,这种方法的局限是求得的是局部优化布局方案;2)研究区的渠道系统并不一定是1棵最小生成树,有可能是2棵或者是3棵。
为能运用最小生成树模型描述土地整治渠道优化布局模型,需做如下假设:1)2组0-1型变量。最小生成树的数学模型是用0-1型变量表示连接节点的弧,现有最小生成树的数学模型只用1组0-1型变量来表示连接节点的弧。但是渠道优化布局模型要处理 2 级不同的渠道的优化布局问题,因此需要2组0-1型变量来表示连接田块重心点的渠道,其中一组表示斗渠,另一组表示农渠;2)虚拟点假设。根据研究区内或周围支渠或支渠以上水源分布情况和研究区平整后的坡度,可以确定其中几个田块作为渠道起始点。因此土地整治研究区灌溉渠道布局方案实际上不是1棵最小生成树,而是几棵最小生成树。为了能运用最小生成树模型需要假设 1 个虚拟点,该点到确定的渠道起始点的距离无限小,但是到其他重心点的距离却无限大;3)可能取水点假设。根据研究区内或周围支渠或支渠以上水源分布情况和研究区平整后的坡度选出来的、作为研究区渠道根节点的重心点,称为可能取水点。研究区只有可能取水点可以和虚拟点连接。
为简化问题,需定义:1)折算比例。因为斗渠与农渠的建造成本不一样,所以需要根据折算比例,将建造成本统一折算到农渠;2)渠道长度约束。根据土地开发整理项目规划设计规范,斗渠和农渠的长度都有 1 个上限;3)渠道分支约束。不管是斗渠还是农渠都不能在中途分叉。
为方便建模引入下列记号:第i个田块斗渠和农渠的长度分别用Ldi、Lni表示;田块之间的距离用Lij表示;单位长度斗渠和农渠的造价分别用Cd和Cn表示;田块重心数量用 n 表示;田块重心集合的任意子集用S表示;农渠0-1型变量用xij表示,0代表i与j间无农渠连接,1代表i与j间有农渠连接;斗渠0-1型变量用yij表示,0代表i与j间无斗渠连接,1代表i与j间有斗渠连接。
2 沟渠优化布局模型
2.1 目标函数
以整个区域灌溉渠道的总造价最小作为目标。
当第i个田块与第j个田块由斗渠连接时,yij的值为1,xij的值为0,则Cd·Lij·yij=Cd·Lij、Cd·Lij·xij=0,其建造成本为Cd·Lij;当第i个田块与第j个田块由农渠连接时,yij的值为0,xij的值为1,则Cn·Lij·xij=Cn·Lij、Cn·Lij·yij=0,其建造成本为Cn·Lij;当第i个田块与第j个田块不连接时,yij的值为0,xij的值为0,则Cd·Lij·yij=Cd·Lij·xij=0,其建造成本为0。总建造成本Z为任意田块之间的建造成本之和,则目标函数为

式(1)以yij和xij为决策变量。沟渠优化布局模型需要对田块间连接方式进行决策,确定yij和xij为0型还是1型变量。
2.2 模型约束条件
2.2.1 树约束
研究区所有田块都需要灌溉,因此需要将田块的重心点连接在一起。为了保证生成的是 1 棵树,连接边的数量比重心点数量少 1 个。由于部分节点之间可能形成环,保证边的数量并不能保证生成的一定是树。因此需要防止环的形成,节点集合的任意子集中其连接边的数量比子集的节点数少1个。只有在这2个约束下才能保证生成的是树,其具体形式如下:
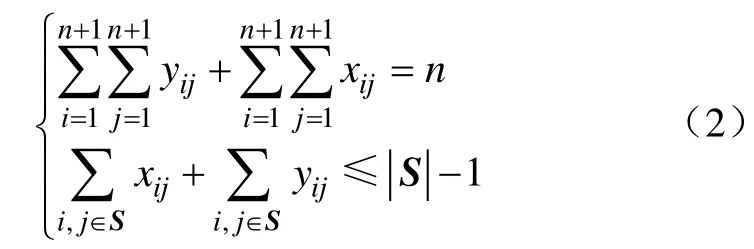
2.2.2 农渠度和斗渠度约束
首先明确2个概念,节点与其他节点连接边的数量称为节点的度,对生成树中各节点度数加上一定限制的最小生成树称为度约束最小生成树。相对于基本最小生成树,该模型与很多实践问题更加接近。例如该文的沟渠优化布局模型必须按照同级渠道不能相连的原则进行布局,即指渠道不能分叉。这就要求1个节点与其他节点连接边的数量应该≤2(1个表示进入,1个表示出去),但是处于渠道末尾的节点则只有1条表示进入的连接边。因此该文的沟渠优化布局模型是度约束最小生成树模型。其具体的农渠度约束形式如下:

上式中的 xij不包括虚拟点。
斗渠度约束与农渠度约束类似,不再赘述,其具体形式如下:

2.2.3 斗渠与农渠互斥约束
第i个重心点与第j个重心点之间只能由斗渠或农渠连接,而不能同时由这两者连接。因此这是该文最小生成树模型特有的约束,因为一般的最小生成树模型只有1个0-1型决策变量,根本就不会有这个问题,只有该文的有2个0-1型决策变量的最小生成树模型才会出现这个问题。因此在 2 个田块之间斗渠与农渠是互斥的,其具体形式如下:

这里包括虚拟点在内。
2.2.4 斗渠和农渠长度约束
斗渠和农渠长度约束的具体形式为

式中Ldmax和Lnmax分别为所有斗渠和农渠长度的最大值,Ldm和Lnm分别为规程规定的斗渠和农渠最大值。这里不包括虚拟点。
2.2.5 可能取水点约束
考虑水源约束,在建立模型时选择水源边的田块作为可能取水点。可能取水点出去的连接只能为斗渠,令k=1,2,…,t为可能取水点,则可能取水点约束的具体形式为

这里不包括虚拟点。
综上,该文建立的沟渠优化布局模型不同于一般的最小生成树模型,一般的最小生成树模型只包括1个0-1型变量,只能处理一级线性工程的优化布局,而该文建立的模型包括2个0-1型变量,能够处理两级线性工程优化布局,这符合实际情况。在实践中很多优化布局问题不仅仅是处理一级线性工程,而是2级甚至多级。如果用一般的最小生成树模型进行二级线性工程的优化布局,首先需要凭经验确定高一级线性工程的布局,然后再运用模型求得次一级线性工程的布局,求得的布局方案是局部最优的方案,具有很大限制。而如果用该文建立的最小生成树模型进行二级线性工程的优化布局,求得的布局方案是全局最优的方案,因此该文建立的模型更符合实际。该文将只有1个0-1型变量的最小生成树模型称为一级最小生成树模型,具有2个0-1型变量的最小生成树模型称为两级最小生成树模型。至此,把沟渠优化布局问题抽象成了具有长度约束、度约束的两级最小生成树模型。
3 沟渠优化布局模型求解方法
采用LINGO软件进行求解。整个模型共3类节点,虚拟点、可能取水点和田块重心点。
3.1 虚拟点处理
研究区可有多个可能取水点,可以生成多条斗渠,从而其渠道布局方案是由多棵生成树组成。虚拟点是多个可能取水点的根节点,虚拟点、虚拟渠道和研究区多棵生成树组成了 1 棵更大的生成树,从而将求解研究区多棵生成树问题转化成求解 1 棵生成树问题。为了在程序中将新增的虚拟点与研究区田块重心点统一处理,而又显示其特殊性,需要对其做如下处理。虚拟点编号:程序中的循环结构和分支结构对数组变量第 1 个值即能将其与后面的值做统一处理,同时也方便将其做特殊处理。因此将虚拟点放在程序节点集合的第1个。
3.2 求解思路
除了斗渠和农渠的长度约束外,模型中其他约束都可以直接用程序语言表示出来。但是长度约束却还要先求出每条农渠和斗渠的长度。因此,该文的沟渠优化布局模型比最小生成树模型更复杂。求解思路是将长度约束剥离出来,然后再利用LINGO求解无长度约束的沟渠优化布局模型。具体方法是先确定斗渠。这些斗渠能使研究区任何地方到斗渠的距离小于农渠的长度约束,而且是最短的,相当于将长度约束剥离出来,且保证了全局最优。然后再利用最小生成树模型求解最短农渠。保证所求的布局方案是工程量最小的。
3.2.1 确定斗渠
斗渠要满足使研究区任何地方到斗渠的距离小于农渠的长度约束,而且满足斗渠长度最短的要求。
借助计算几何中的凸壳理论,先求研究区边界的凸壳;然后求研究区边界的最小外圆;最后求研究区边界最小外圆的一个划分,该划分使研究区边界最小外圆的任何地方到划分该圆的线段的距离都小于农渠约束距离,且这些线段的总长度是最短的。这样就把确定满足要求的斗渠问题转化成了较简单的几何问题。
1)研究区边界凸壳。研究区边界是平面多边形,其顶点凸壳是指包括平面多边形顶点的最小凸集。而凸集是指平面上点集中的任意 2 点所连接线段全部位于其内部的非空点集。平面多边形顶点凸壳边界是凸多边形,其顶点为多边形顶点中的点。如图2所示,平面多边形ABCDEFG的凸壳是点集{A,B,C,E,F,G},凸壳边界是凸多边形ABCEFG。
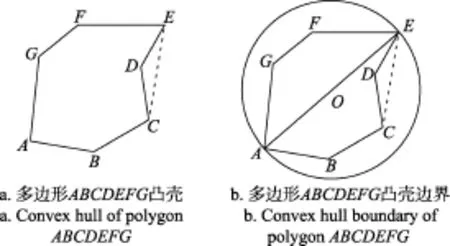
图2 平面多边形凸壳及其边界示意图Fig.2 Diagram of planar polygon convex hull and its boundary
2)研究区边界的最小覆盖圆。平面凸多边形直径是凸多边形顶点间最远的点对之间的距离。平面凸多边形的最小覆盖圆是指包括平面多边形的最小覆盖圆。如图2所示,设凸多边形覆盖圆直径为AE,AE中点为O,O到凸多边形中其他各点的距离必有最大值rm,假设该点为A。若rm≤|AE|/2,则以AB为直径的圆即是该凸多边形的最小覆盖圆。否则以O为圆心、rm为半径的圆为最小覆盖圆。
3)研究区斗渠确定。该文讨论的范围是研究区最小外圆的半径>600 m及<2 400 m的土地整治项目。因为当圆的半径为600 m时,面积为113.04 hm2,当圆的半径为1 200 m时,面积为452.16 hm2,当半径为2 400 m,面积为1 809.50 hm2。一般来说土地整治项目的面积不会太小但也不会大于1 000 hm2,所以研究区外接圆的半径基本>600 m及<2 400 m,因此该文讨论的范围就是研究区最小外圆的半径>600 m及<2 400 m的土地整治项目。
当研究区半径>600 m及<1 200 m时,如图3a所示,图中大圆为研究区边界最小外圆,设其半径为X,小圆半径为1 200-X,则通过可能取水点A且相交于小圆的所有斗渠都能满足大圆上所有点到该斗渠的距离都<1 200 m,通过可能取水点A且相切于小圆的斗渠AD满足大圆上所有点到该斗渠的距离≤1 200 m,而且距离的最大值为线段BC的长度1 200 m。通过可能取水点A且相离于小圆的斗渠AF则不能满足大圆上所有点到该斗渠的距离都≤1 200 m,如弧HCI到该斗渠的距离>1 200 m,要使大圆上所有点到斗渠的距离<1 200 m,必须将斗渠AF变成斗渠ABF。从图中可以看出AD是所有满足要求的斗渠中长度最短的,因此当研究区半径>600 m及<1 200 m时,满足要求的最短的斗渠为AD。

图3 研究区最短斗渠示意图Fig.3 Diagram of shortest lateral canal in study area
2)当研究区半径等于1 200 m时,如图3b所示,图中圆为研究区边界最小外圆,其半径为1 200 m,则通过可能取水点A、圆心O的斗渠能满足大圆上所有点到该斗渠的距离≤1 200 m,而通过可能取水点A的斗渠AF则不能满足大圆上所有点到该斗渠的距离≤1 200 m,如弧HI到该斗渠的距离>1 200 m,要使大圆上所有点到斗渠的距离<1 200 m,必须将斗渠AF变成斗渠AOF。从图中可以看出AE是所有满足要求的斗渠中长度最短的,因此当研究区半径等于1 200 m时,满足要求的最短的斗渠为AE。
3)当研究区半径>1 200~1 800 m时,如图3c所示,图中圆为研究区边界最小外圆,EF和EI长度为1 200 m,CB和DH的长度必定<1 200 m,设其半径为X。因为其半径>1 200 m,所以1条斗渠不能满足圆上所有的点到斗渠的距离≤1 200 m,而是需要2条,图中斗渠AF和AI就是满足要求的最短的斗渠。
4)当研究区半径>1 800~2 400 m时,如图3d所示,图中圆为研究区边界最小外圆,EF、EI、CB、DH的长度为1 200 m。斗渠ACF和ADI为满足要求的最短的斗渠。
3.2.2 无长度约束沟渠优化布局模型
无长度约束沟渠优化布局模型是指剔除斗渠和农渠长度约束后的沟渠优化布局模型[28-30]。该模型可以直接用LINGO求解。
4 案例分析
4.1 研究区概况
研究区位于安徽省宿州市埇桥区蕲县镇忠陈村(117°3'~117°5'E、33°24'~33°25'2N),属于采煤塌陷区。研究区于2011年进行土地整理项目,笔者于2011年参与该项目的规划设计。笔者在对该区进行渠道系统布置时发现现有渠道布置方法不能根据各级渠道造价建立优化模型选择最优的布局方案。因此笔者根据材料信息价及渠道结构设计得到各级渠道单位长度的造价,并基于研究区田块通过Arcgis软件处理获得田块重心点及各田块之间的距离等基础数据代入本文建立的模型进行求解。
4.2 结果与分析
4.2.1 研究区斗渠布局方案
画出研究区边界的最小覆盖圆后,作过可能取水点的最小覆盖圆的直径,因为有2个可能取水点,需要选出1个更合适的。对比这2条直径的走向与研究区主要规划道路的走向,选择其中与研究区主要规划道路的走向更接近的直径,连接该直径经过的田块的重心点作为研究区斗渠。斗渠具体布局方案见图4。

图4 研究区斗渠布局图Fig. 4 Layout of lateral canal in study area
4.2.2 研究区渠道布局方案
确定研究区斗渠后,将对应的yij赋值为1,然后运行运用LINGO编写的无长度约束沟渠优化布局模型求解程序,得到如图5a所示的研究区渠道系统。共斗渠1条,长2 811 m,农渠22条,长17 712 m,共20 523 m。根据优化原则布设,且已通过评审的渠道布局方案如图 5 b所示,共有斗渠2条,长6 037 m,农渠23条,长14 535 m。共20 572 m。
通常土地整治工程设计中斗渠设计为口宽150 cm,底宽50 cm,深100 cm的梯形;农渠设计为口宽80 cm,深90 cm的矩形。斗渠每米工程量是1 m3,农渠每米工程量是0.75 m3,斗渠单位长度的工程量是农渠单位长度工程量的 1 .33倍。这样换算出来模型优化方案的工程量是16 095 m3,评审方案的工程量是16 938.25 m3,模型优化方案的工程量比评审方案的工程量减少了5%,按斗渠工程2011年当地单价85元/m,农渠工程2011年当地单价49.58元/m,可节约工程造价116 694元。

图5 基于不同方法的研究区渠道布局图Fig.5 Canal layout in study area based on different methods

表1 渠道布局方案比较Table 1 Comparison of canal layout methods
5 结论与讨论
该文运用最小生成树理论对土地整治项目渠道布局进行描述,并结合虚拟点、可能取水点、分权重定义节点建立了基于最小生成树理论的优化模型。该模型能够反映平原地区土地整治项目渠道布局的分级情况、多取水点情况,并能利用成熟的最小生成树理论的求解方法进行求解。最后通过实例分析表明,基于最小生成树的渠道布局比基于优化原则的布局节省5%的工程量,验证了该模型的实用性。但是该模型还有一些未考虑到的地方,使得该模型具有一定的局限性,希望进一步的研究将这些因素考虑进来完善渠道优化布局模型,具体如下:1)该研究斗、农渠单位长度的造价是根据多年设计平原地区渠道的经验确定的,没有考虑斗、农渠设计尺寸的概率分布,没进行严格的统计学处理,得到的结果有一定的误差。进一步的研究需要积累设计数据,得出斗、农渠设计尺寸的概率分布,对设计尺寸进行严格的统计学处理,使研究结果具有更广泛的适用性;2)该文的渠道优化布局模型虽然通过可能取水点概念的提出,考虑了水源约束。但是该文的研究区是平原地区,整个研究区高差很小,未考虑地形约束和上下级渠道、各取水点的水位约束。因此该模型只适用于平原地区的渠道优化布局,为了推广至其他区域,需要进一步的研究来完善模型。此外,该文模型只考虑了渠道的投资,未考虑灌溉、排水系统及道路等交叉建筑物的投资。因此该模型得到的最优方案只是灌溉渠道的最优布局方案,为了降低整个研究区总的投资,需要进一步将灌溉系统、排水系统、道路系统及其交叉建筑物投资纳入模型内,构建综合模型。
[1] 刘飞,陆林. 采煤塌陷区的生态恢复研究进展[J]. 自然资源学报. 2009,24(4):612-620. Liu Fei,Lu Lin. Progress in the study of ecological restoration of coa1 mining subsidence areas[J]. Journal of Natural Resources,2009,24(4):612-620.(in Chinese with English abstract)
[2] 胡振琪,赵艳玲,程玲玲. 中国土地复垦目标与内涵扩展[J]. 中国土地科学,2004,18(3):3-8. Hu Zhenqi,Zhao Yanling,Cheng Lingling. Extension of goal and meaning of land reclamation in china[J]. China Land Science,2004,18(3):3-8.(in Chinese with English abstract)
[3] 周复旦,赵长胜,丁佩,等. 任楼矿区塌陷土地复垦规划与利用现状研究[J]. 水土保持通报,2011,31(1):227-230. Zhou Fudan,Zhao Changsheng,Ding Pei,et al. Reclamation planning and use status of subsided lands in Renlou mining area[J]. Bulletin of Soil and Water Conservation,2011,31(1):227-230.(in Chinese with English abstract)
[4] 赵艳玲,黄琴焕,薛静,等. 矿区土地复垦方案编制中土地破坏程度评价研究[J]. 金属矿山,2009,395(5):161-163. Zhao Yanling,Huang Qinhuan,Xue Jing,et al. Study on the assessment of land destroy degree in mine land reclamation design[J]. Metal Mine,2009,395(5):161-163.(in Chinese with English abstract)
[5] 蒋俊峰,赵琼祥,高议民. 我国矿区废弃区土地复垦技术的研究[J]. 山西煤炭,2010,30(6):74-76. Jiang Junfeng,Zhao Qiongxiang,Gao Yimin. China’s land reclamation technology research of abandoned mining area [J]. Shanxi Coal,2010,30(6):74-76.(in Chinese with English abstract)
[6] 冯小军,陈宇,魏颖. 我国矿区废弃区土地复垦技术研究[J]. 煤,2009,18(10):1-5. Feng Xiaojun,Chen Yu,Wei Ying. Technology research of reclaimed abandoned mine land in china[J]. Coal,2009,18(10):1-5.(in Chinese with English abstract)
[7] 陈秋成,卞正富. 矿区土地复垦规划决策支持系统开发[J].地理空间信息,2008,6(4):98-100. Chen Qiucheng,Bian Zhengfu. Development of land reclamation planning decision support system in mining areas [J]. Geospatial Information,2008,6(4):98-100.(in Chinese with English abstract)
[8] 卞正富. 国内外煤矿区土地复垦研究综述[J]. 中国土地科学,2000,14(1):6-11.
[9] 张洪波,陈秋计,谢宏全,等. 矿区复垦土地资源优化配置方法研究[J]. 西安科技大学学报,2005,25(2):172-174. Zhang Hongbo,Chen Qiuji,Xie Hongquan,et al. Optimization configuration method of reclamation land resources in mining area[J]. Journal Of Xi’an University Of Science And Technology,2005,25(2):172-174.(in Chinese with English abstract)
[10] 罗仪宁. DEM表面地形突变特征表达方法研究[D]. 西安:西北大学,2011. Luo Yining. Method of the Representation for Artificial Discontinuous Terrain on the DEM Surface[D]. Xi’an:Northwest University,2011.(in Chinese with English abstract)
[11] 胡晋山,康建荣,吴志强,等. 基于GIS的矿区地表塌陷预计及规划治理系统的设计[J]. 现代矿业,2010,496(8):52-54.
[12] 王慎敏,金晓斌,周寅康. 基于GIS的采煤塌陷区土地复垦项目规划设计研究[J]. 地理科学,2008,28(2):195-199. Wang Shenmin,Jin Xiaobin,Zhou Yinkang. Planning and designing of reclamation project in mining subsided land based on GIS[J]. Scientia Geographica Sinica,2008,28(2):195-199.(in Chinese with English abstract)
[13] 刘玉华. 煤矿区土地复垦管理信息系统的设计与应用[D].济南:山东师范大学,2008. Liu Yuhua. Design and Apply in Land Reclamation Management Information System of Coal Mining Area[D]. Ji’nan:Shandong Normal University,2008.(in Chinese with English abstract)
[14] 胡晋山,康建荣,王文福. 基于GIS的矿区土地复垦信息系统的设计[J]. 金属矿山,2010,414(12):113-116. Hu Jinshan,Kang Jianrong,Wang Wenfu. Design of information system of mine land reclamation based on GIS[J]. Metal Mine,2010,414(12):113-116.(in Chinese with English abstract)
[15] 付浩,催玉朝,奚新丽. GIS在矿区复垦土地相关模型中的耦合应用[J]. 矿业工程,2009,7(2):57-59. Fu Hao,Cui Yuchao,Xi Xinli. Application of GIS based land reclamation models[J]. Mining Engineering,2009,7(2):57-59.(in Chinese with English abstract)
[16] 黄琪. 基于DEM与LP的土地平整工程设计优化研究[D].南京:南京农业大学,2011. Huang Qi. Study on Optimal Design for Land Leveling Project based on DEM and LP[D]. Nanjing:Nanjing Agricultural University,2011.(in Chinese with English abstract)
[17] 胡振琪. 土地复垦与生态重建[M]. 徐州:中国矿业大学出版社,2008.
[18] 江帆. DEM表面建模与精度评估方法研究[D]. 郑州:解放军信息工程大学,2006. Jiang Fan. Researches on the Surface Modeling and the Accuracy Evaluation of DEM[D]. Zhenzhou:The PLA Information Engineering University,2006.(in Chinese with English abstract)
[19] 曲世洁. GIS结合 E xcel在土方计算及调配中的应用研究[D]. 大连:大连理工大学,2011. Qu Shijie. Application Research of GIS Combined with Excel for Calculating Earthwork and Earth Dispensation[D]. Dalian:Dalian University of Technology,2011.(in Chinese with English abstract)
[20] 柳长顺,齐实,杜丽娟. 土地整理项目土方量计算方法[J].中国水土保持科学. 2003,1(2):77-79. Liu Changshun,Qi Shi,Du Lijuan. Method to calculate earthwork in land consolidation project[J]. Science of Soil and Water Conservation,2003,1(2):77-79.(in Chinese with English abstract)
[21] 陆锋. 最短路径算法:分类体系与研究进展[J]. 测绘学报,2001(3):269-275. Lu Feng. Shortest path algorithms:Taxonomy and advance in research[J]. Acta Geodaetica et Cartographica Sinaca,2001(3):269-275.(in Chinese with English abstract)
[22] 赵艳玲,胡振琪,高永光,等. ERDAS IMAGINE在采煤沉陷地复垦土方量计算中的应用[J]. 矿业研究与开发,2005,25(2):82-88. Zhao Yanling,Hu Zhengqi,Gao Yongguang,et al. Application of ERDAS IMAGINE in the earthwork calculation of subsided land reclamation for coal mining[J]. Mining Research and Development,2005,25(2):82-88.(in Chinese with English abstract)
[23] 付梅臣,胡振琪,米静. 土地整理和复垦工程费用结构分析及控制对策研究[J]. 农业工程学报,2003,19(4):291-294. Fu Meichen,Hu Zhenqi,Mi Jing. Contribution analyses and control countermeasures of land consolidation and reclamation project cost[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2003,19(4):291-294.(in Chinese with English abstract)
[24] 石磊,冯祖针,杨建强,等. 度-半径约束最小生成树问题及其算法[J]. 沈阳大学学报,2012,24(4):63-66. Shi Lei,Feng Zuzhen,Yang Jianqiang,et al. Degreeconstrained,radius-constrained minimum spanning tree problem and its algorithm[J]. Journal of Shenyang University,2012,24(4):63-66.(in Chinese with English abstract)
[25] 蒋晓红,程吉林,曾庆祝. 平原河网地区灌溉泵站群优化布局研究[J]. 灌溉排水学报,2009(4):52-54. Jiang Xiaohong,Cheng Jilin,Zeng Qinzhu. The layout optimization of irrigation pumping stations in plain river network region[J]. Journal of Irrigation and Drainage,2009(4):52-54.(in Chinese with English abstract)
[26] 许夕保,周振红,程吉林. 渠道简化设计[J]. 中国农村水利水电,1997(9):25-27. Xu Xibao,Zhou Zhenhong,Cheng Jilin. Simplified design to Canal[J]. China Rural Water and Hydropower,1997(9):25-27.(in Chinese with English abstract)
[27] 程吉林,毕荣石. 渠道设计的动态规划模型[J]. 灌溉排水,1991(1):53-56. Cheng Jilin,Bi Rongshi. Dynamic programming model of canal design[J]. Irrigation and Drainage,1991(1):53-56.(in Chinese with English abstract)
[28] 仇锦先,程吉林,吕赛军. 渠系网络图在大型灌区规划中的应用[J]. 中国农村水利水电,2004(1):56-58. Chou Jinxian,Cheng Jilin,Lü Saijun. Application of network diagrams of canal system in large-sized irrigation districts planning[J]. China Rural Water and Hydropower,2004(1):56-58.(in Chinese with English abstract)
[29] 程吉林,陈平,朱春龙. 输水渠道线路优化与漫游数学家模型[J]. 水科学进展,2004(3):397-399. Cheng Jilin,Chen Pin,Zhu Chunlong. Optimal alignment of channel and wanderings mathematician model[J]. Advances in Water Science,2004(3):397-399.(in Chinese with English abstract)
[30] 周荣敏,雷延峰. 不同灌溉工作制度下的灌溉管网优化设计研究[J]. 西北水资源与水工程,2002,13(2):1-5. Zhou Rongmin,Lei Yanfeng. Study on optimization design f or irrigation pipe network under different irrigation schedules[J]. Northwest Water Resources &Water Engineering,2002,13(2):1-5.(in Chinese with English abstract)
Optimal model of channel layout based on minimum spanning trees
Xu Zichang
(1. School of Earth Resources,China University of Geosciences(Wuhan),Wuhan 430074,China;2. Fujian Geologic Surveying and Mapping Institute of Remote Sensing Center,Fuzhou 350011,China)
Few studies have been done on the layout of ditches,and the quantitative models for the optimization of the channel layout is lacking. Since the cost of channel layout project accounts for a large proportion of the cost of land reclamation project,it is necessary to find a design in order to reduce the cost of channel project. In this paper,a new model was developed for optimal layout of canals and ditches. The theory of minimum spanning tree was used to describe the channel layout of land reclamation project,and an optimal model based on minimum spanning tree theory was established in combination with the virtual point,the alternative water intake point and the weighted definition node. The study area was located at a coal mining subsidence area in Yongqiao District,Suzhou City,Anhui Province(33°24'-33°25'N and 117°3'-117°5'E). The channel optimization layout model based on the minimum spanning tree was constructed to optimize the layout of farmland irrigation channels in the plain areas. Different from the traditional minimum spanning tree model,this model solved the optimization problem for two-level channels,and the final solution using this model was greater than or equal to a minimum spanning tree. In order to take advantage of the mature minimum- production-tree approach,the virtual point concept was created to eliminate the difference between the channel optimization layout model and the traditional minimum spanning tree model. Four cases of solving the model were discussed by convex hull theory. The LINGO program was written for solving the model. Finally,the channel optimization model based on the minimum spanning tree was applied to a research area,and then the channel layout scheme using this model was obtained with a total length of 20 523 m containing 1 lateral canal(2 811-m length) and 22 ditches(17 712-m length). According to the traditional optimum principle,there were totally 20 572 m with 2 lateral canals(6 037-m length) and 23 ditches(14 535-m length). The lateral canal was designed as a trapezoid for the land reclamation with a mouth width of 150 cm,a base width of 50 cm and a depth of 100 cm. The ditch was designed as a rectangle with a mouth width of 80 cm and a depth of 90 cm. For the lateral canal,the engineering workload of unit length was 1 m3and for ditch engineering workload per unit length was 0.75 m3. The unit length engineering workload of the lateral canal was 1.33 times of the ditch. Based on unit length engineering workload mentioned above,the total engineering workload of the land reclamation project was 16 095 m3by using the channel optimization layout method based on minimum spanning tree and 16 938.25 m3by using optimum principle method,respectively. The engineering workload of the minimum spanning tree method was 5.0% less than that of the optimum principle. According to the unit price of the lateral canal engineering project 85 yuan per meter and the unit price of ditch engineering 49.58 yuan per meter,the project cost of 116 694 yuan was saved. The result shows that the channel optimization model based on the minimum spanning tree can obtain the channel layout plan with less cost,that is,the maximum control of land reclamation cost. This study can provide an effective way to cost control of land reclamation projects.
canals;optimal systems;land reclamation;layout;minimum spanning tree model;convex hull theory;LINGO
10.11975/j.issn.1002-6819.2017.01.017
F301.24
A
1002-6819(2017)-01-0124-07
许自昌. 基于最小生成树的渠道系统优化布局模型[J]. 农业工程学报,2017,33(1):124-130.
10.1197 5/j.issn.1002-6819.2017.01.017 http://www.tcsae.org
Xu Zichang.Optimal model of channel layout based on minimum spanning trees [J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2017,33(1):124-130.(in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2017.01.017 http://www.tcsae.org
2016-03-30
2016-11-07
国土资源部公益性行业科研专项课题(201011016-2)
许自昌,男,江西抚州人,博士生,高级工程师,中国土地估价师,中国房地产估价师,主要从事土地管理、土地规划、土地整理设计、矿山复垦等研究。武汉 中国地质大学(武汉)资源学院,430074。Email:120433676@qq.com

