液压油箱内部隔板对气泡分离的影响

马晓霞,冀 宏,郑 直,张继铭

(1.兰州理工大学能源与动力工程学院,甘肃兰州 730050; 2.甘肃省液压气动工程技术研究中心,甘肃兰州 730050)

液压油箱内部隔板对气泡分离的影响

马晓霞1,2,冀 宏1,2,郑 直1,2,张继铭1,2

(1.兰州理工大学能源与动力工程学院,甘肃兰州 730050; 2.甘肃省液压气动工程技术研究中心,甘肃兰州 730050)

利用Fluent中的欧拉-欧拉多相流模型,对一种液压油箱内部流场进行气液两相流三维数值计算,验证了气泡在油液中上浮的时间随其直径的增大而缩短的变化规律,对比分析了有无隔板以及隔板位置不同时,油液中不同直径气泡的分离特点。结果表明:隔板对直径为0.3～1.0 mm的气泡分离影响明显,通过隔板延长油液流动距离,有利于气泡的上浮分离;直径为1～2 mm的气泡,本身上浮时间比较短,几乎完全可以从油液中分离,隔板对大气泡分离影响很小。

液压油箱;上浮时间;隔板;气泡直径;气泡分离

在液压系统中,油箱是液压系统的重要组成部分,其主要作用是储存液压系统循环所需的油液、散热以及分离油液中的空气等[1,2]。而油液中气泡的存在会导致系统出现气穴、噪声等问题,严重危害着系统的可靠性和稳定性[3]。因此,分离油液中的空气是十分必要的,近年来国内外针对气泡分离方法的研究,主要采用强制式气泡去除方法,例如通过气液旋流分离器[4-6]、油液流动扰流器[7]来分离气泡。

目前,液压系统向着小型化方向发展,但液压系统的小型化离不开液压油箱的小型化[8]。液压油箱的小型化意味着油液在油箱内循环的时间变短,并且油液中气泡的分离时间也缩短,因此,为了避免这些问题,必须重视油箱的结构设计[9]。在油箱中设置隔板,可延长油液在油箱内的停留时间并引导液压油在油箱中的合理流向,使气泡有更多的时间浮出,以免被泵再次吸入。

气泡作为分散相,在粘性液体中的运动分布是一个典型的气液两相流动现象[10]。研究利用Fluent中的欧拉-欧拉多相流模型对液压油箱内部流场进行气液两相流三维数值计算,分析了不同直径的气泡在油箱内的分布特点,对比三种隔板设置方式对泵吸油口气泡含量的影响,为液压油箱内隔板的设置提供参考依据。

1 油箱的CFD计算模型与计算条件

1.1 计算模型

图1为液压油箱(尺寸:500 mm×200 mm× 300 mm)的三维CFD几何模型,计算区域为油箱回油口到油箱吸油口的流体区域。

模型1:油箱内不加隔板;

模型2:加置隔板后,油液如图1(b)所示的流向流动,隔板1、隔板2厚度为3 mm,宽度为195 mm,高度为200 mm;

模型3:加置隔板后,油液如图1(c)所示的流向流动,隔板Ⅰ、隔板Ⅱ厚度为3 mm,宽度为165 mm,高度为295 mm;

模型4:隔板长度为435 mm,厚度为3 mm,高度为295 mm。

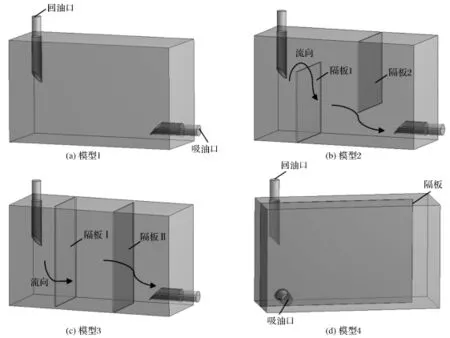
图1 三维CFD几何模型Fig.1 3D CFD geometry model

1.2 网格划分

为了获得较为准确的计算结果,网格需进行局部细化,吸油管路、回油管路表面以及隔板表面边界层都需要至少5层网格,计算模型的网格单元总数大约为350万,网格质量为0.8左右。模型3的网格生成模型如图2所示。

图2 模型3的网格生成模型Fig.2 Model diagram of mesh generation of Model 3

1.3 计算条件

Fluent提供的多相流模型中,欧拉模型适用于弥散相集中于计算域的局部和有一相混合或分离的场合,采用Fluent欧拉-欧拉模型的SST湍流模型对主相(液压油)和离散相(气泡)进行仿真计算。在该模型中,气泡也作为连续相处理并占有一定的体积分数。

混入液压油中的空气主要是以气泡形式存在,假设气泡为理想球体,气泡大小通过在分相中设置直径大小来确定,气泡参数按理想气体取值。

介质物性参数:油液密度为860 kg/m3,动力粘度为0.039 56 kg/m·s,运动粘度为46 mm2/s,油液温度为40℃。

边界条件设置:进口边界条件为压力进口,相对压力为0,气泡的体积分数为8%,气体密度设为1.225 kg/m3,气体粘度为1×10－5kg/m·s;出口边界条件为速度出口,速度为0.54 m/s;油箱流域上表面设置排气条件,排气代替自由表面流动。

该计算采用三维瞬态计算,收敛残差精度取10－6,进、出口流量误差小于5%时认为计算收敛。

2 气泡在油箱内的分布

2.1 不同直径气泡的分布特点

以图1(a)所示模型1的内流场分布为例,分析不同直径气泡的分布特点。进口气体体积分数为8%,气泡直径d分别取为0.3 mm、0.5 mm、1.0 mm、1.5 mm、2.0 mm。图3为模型1气泡直径d取0.5 mm时的气体体积分数分布云图。

油液由回油口冲入油箱,在油箱底部形成漩涡,气泡随着油液一部分上浮出液面,一部分被带入吸油口。由图3可知,油箱内气体体积分数平均值约为7%;与油箱内其他区域相比,油液上表面气体体积分数偏大,油箱底部气泡含量最低,气体体积分数最小值为0.5%;吸油管上表面气泡聚集最多,气体体积分数约为6.5%。

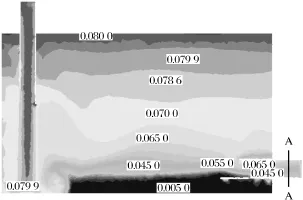
图3 模型1气体体积分数分布云图Fig.3 Cloud chart of gas volume fraction distribution of Model 1

为了定量分析不同直径的气泡的分布特点,取吸油口A-A截面处的气体体积分数平均值进行统计分析,如图4所示。

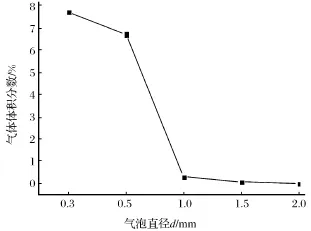
图4 气体体积分数随气泡直径的变化曲线Fig.4 Changing curve of gas volume fraction with bubble diameter

图4给出了吸油口A-A截面处的气体体积分数随气泡直径的变化情况。由图4可以看出,当气泡直径在0.3～1.0 mm之间增大时,吸油口A-A截面处的气体体积分数随之减小;气泡直径为0.3 mm、0.5 mm、1.0 mm时,吸油口A-A截面处的气体体积分数平均值分别为7.73%、6.72%、0.29%,与进口气体体积分数8.00%相比,气体体积分数平均值分别降低了0.27%、1.28%、7.71%;当气泡直径在1～2 mm之间增大时,吸油口A-A截面处的气体体积分数减小幅度变小;气泡直径为

1.5 mm、2.0 mm时,吸油口A-A截面处的气体体积分数平均值几乎为零。

液压系统工作时,回油油液会携带空气流入到油箱内,油箱内油液的紊流流动和局部的气穴都会促使油液中的空气形成气泡,部分气泡会上浮到液面,从油液中逸出,其上升时间会受到直径大小、油液粘度等因素的影响。

一般地,气泡上浮1 m所需的时间为[9]

其中:T为气泡上浮1 m所需时间(min);18为常量;d为气泡直径(mm);g为重力加速度(m/s2);v为运动粘度(mm2/s)。

由式(1)可知,气泡上浮1 m所需的时间与其直径d的平方成反比,即气泡直径越大,上浮1 m所需的时间越短。

根据前述可知v＝46 mm2/s,由式(1)可得,当气泡直径d为0.3 mm、0.5 mm、1.0 mm、1.5 mm、2.0 mm时,气泡在油液中上浮1 m所用时间分别为15.63 min、5.63 min、1.41 min、0.63 min、0.35 min。油液中气泡上浮1 m所需时间随气泡直径大小的变化规律如图5所示。

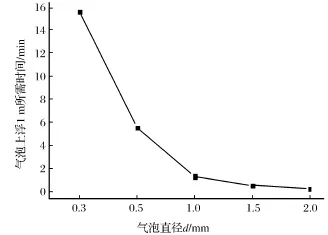
图5 气泡上浮时间随其直径的变化曲线Fig.5 Changing curve of bubble floating time with their diameter

结合图4与图5知,随着气泡直径d在0.3～2 mm之间增大,气泡上浮的时间缩短,进口气体体积分数一定时,随着油液到达吸油口的气泡就会减少,即吸油口A-A截面处的气体体积分数减小。

2.2 隔板位置对气泡分离的影响

图6为气泡直径d取0.5 mm时模型2、模型3、模型4的气体体积分数分布云图。由图6可知,模型2、模型3、模型4中,油箱内气体体积分数平均值分别约为7.7%、7.5%、6.0%;油箱底部气泡含量最低,气体体积分数最小值分别为2.0%、0.5%、0.5%;吸油管上表面气泡聚集最多,气体体积分数分别约为6.9%、6.0%、5.5%。

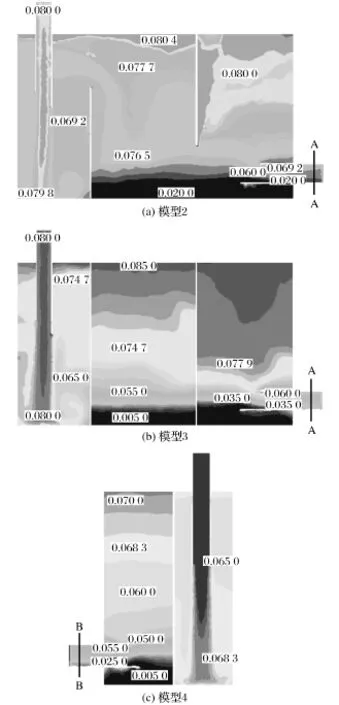
图6 气体体积分数分布云图Fig.6 Cloud chart of gas volume fraction distribution

结合图3中模型1与图6中模型2、模型3、模型4的内流场分布,对比分析无隔板与隔板在不同位置时气泡的分离特点。模型1、模型2、模型3均取吸油口A-A截面处的气体体积分数平均值,模型4取吸油口B-B截面处的气体体积分数平均值,对以上四种模型指定截面处的气体体积分数平均值进行对比分析。

图7给出了四种模型吸油口指定截面处的气体体积分数随气泡直径的对比变化情况,每条曲线上的5个点分别代表气泡直径为0.3 mm、0.5 mm、1.0 mm、1.5 mm、2.0 mm时,吸油口指定截面处的气体体积分数平均值。

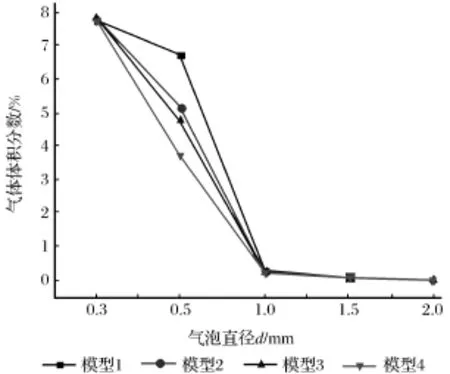
图7 气体体积分数随气泡直径的变化曲线Fig.7 Changing curve of gas volume fraction with the bubble diameter

将图7中模型1与模型2、模型3、模型4对比可得:气泡直径在0.3～2.0 mm之间增大时,四种模型吸油口截面处的气体体积分数均减小,且加置隔板时,吸油口截面处的气体体积分数平均值均小于无隔板时的气体体积分数平均值;气泡直径在0.3～1.0 mm范围内增大时,加置隔板的模型对气泡分离的影响显著;当气泡直径为0.5 mm时,模型1吸油口A-A截面处的气体体积分数平均值约为6.72%,模型4吸油口B-B截面处的气体体积分数平均值为3.71%,吸油口截面处的气体体积分数平均值最高可减小3.01%;气泡直径在1.0～2.0 mm之间增大时,四种模型吸油口截面处的气体体积分数平均值几乎为零。因为由图5可得,气泡直径大于1 mm时,气泡浮出液面的时间比较短,油液中的气泡几乎完全可以依靠自身上浮得以分离,所以吸油口处的气泡含量几乎为零。

由模型2、模型3与模型4可得:隔板位置不同,气泡直径在0.3～1.0 mm之间增大时,吸油口截面处的气体体积分数也不同,模型4吸油口截面处的气体体积分数平均值均比模型2、模型3吸油口截面处的气体体积分数平均值低,因为模型4中,油液在油箱中停留的时间最长,气泡有更多时间上浮,所以吸油口截面处的气体体积分数平均值会更小;当气泡直径为0.5 mm时,模型2、模型3吸油口A-A截面处的气体体积分数平均值分别为5.17%、4.71%,模型4吸油口B-B截面处的气体体积分数平均值为3.71%,这三种模型吸油口截面处的气体体积分数平均值最大相差1.46%;气泡直径在1.0～2.0 mm之间增大时,隔板位置对气泡分离的影响不太明显,因为油液中气泡已靠自身上浮得以分离。

3 结论

对一种尺寸为500 mm×200 mm×300 mm油箱内的气液两相流进行流场仿真计算,验证了气泡在油液中上升的时间随其直径的增大而缩短的变化规律,对比分析了有无隔板以及隔板位置不同时,油液中气泡的分离特点,得到以下结论:

(1)隔板对直径为0.3～1.0 mm的气泡分离影响明显,通过隔板延长流动距离,有利于气泡的分离;

(2)直径为1.0～2.0 mm的气泡本身上浮时间比较短,几乎完全可以从油液中分离,隔板对大气泡分离影响很小;

(3)为了提高油液中气泡的分离效率,可以考虑将小直径气泡积聚成大直径气泡。

[1] 李玉琳.液压元件与系统设计[M].北京:北京航空航天大学出版社,1991.

[2] 王得胜,周爱平.液压系统油箱的优化设计方法研究[J].河南理工大学学报:自然科学版,2012,30(6):690-694.

[3] Johannes Untch,Thees Vollmer,Thorsten Lang.Approach for the Investigation and Evaluation of Hydraulic Tank Designs Regarding Air in Oil Behavior[C]//9th International Fluid Power Conference,Aachen,Germany,2014.

[4] Hui Ji,Songlin Nie,Yun Cheng,et al.Research on the Cone Angle in a Hydrocyclone Separator Used in Hydraulic Oil Purification[C]//Proceeding of the 8th International Conference on Fluid Power Transmission and Control,Hangzhou, China,2013.

[5] Sayako SAKAMA,Yutaka TANAKA,Ryushi SUZUKI.Performance Evaluation of Bubble Eliminator Using Swirl Flow in Hydraulic Systems[C]//Proceeding of the 8th International Conference on Fluid Power Transmission and Control, Hangzhou,China,2013.

[6] Ryushi Suzuki,Koichi Nagaishi,Yutaka Tanaka.Bubble Elimination for Efficiency Through Fluid Power[C]//7th International Fluid Power Conference,Aachen,Germany,2010.

[7] 孙东宁,刘新强,王金林,等.一体化电动液压动力单元内气泡分布及气泡分离方法的研究[J].甘肃科学学报,2015,27(2):88-92.

[8] 祁冠芳,张蕉蕉,孙家根.液压油箱小型化及研发新动向[J].机床与液压,2012,39(24):66-68,104.

[9] Wolfgang Bock,Jurgen Braun,Nancy Puhl,et al.Air Release Properties of Hydraulic Fluids,Dynamic Air Release Behaviour[C]//8th International Fluid Power Conference,Aachen, 2010.

[10] 王焕然,李彦鹏,杨栋,等.黏性液体中单个气泡上升的形状特性[J].工程热物理学报,2009,30(9):1 492-1 494.

The Influence of Hydraulic Oil Container＇s Internal Separator on Bubble Separatio

Ma Xiaoxia1,2,Ji Hong1,2,Zheng Zhi1,2,Zhang Jiming1,2
(1.College of Energy and Power Engineering,Lanzhou University of Technology,Lanzhou730050,China; 2.Research Center for Hy draulics and Pneumatics Engineering of Gansu Province,Lanzhou730050,China)

This papers uses the Euler-Euler Multiphase Model in the Fluent to make gas liquid two-phase flow three dimensional numerical calculation on a certain hydraulic oil tank inner flow field,verifying the change rule that bubble＇s ascent time in the oil will shorten with its diameter increase.It also makes comparative analysis of the separation characteristics of different diameter bubbles in the oil with or without separator and in different separator positions.The results shows that:the separator has great influence on the 0.3～1.0 mm diameter of bubbles.Extend the oil flow distance through the separator can help bubbles float separation.

Hydraulic reservoir;Floating time;Baffle;Bubble diameter;Bubble separation

TH137

:A

:1004-0366(2016)05-0051-05

2015-03-23;

:2015-05-16.

国家自然科学基金(51465033).

马晓霞(1989-),女,甘肃张掖人,硕士,研究方向为流体传动与控制技术.E-mail:mxx_410＠163.com.

Ma Xiaoxia,Ji Hong,Zheng Zhi,et al.The Influence of Hydraulic Oil Container＇s Internal Separator on Bubble Separatio[J].Journal of Gansu Sciences,2016,28(5):51-55.[马晓霞,冀宏,郑直,等.液压油箱内部隔板对气泡分离的影响[J].甘肃科学学报,2016,28(5):51-55.]

10.16468/j.cnkii.ssn1004-0366.2016.05.013.