改进的BP小波神经网络预测模型应用研究
余 兰,岳建平
(河海大学地球科学与工程学院,江苏南京 211100)
改进的BP小波神经网络预测模型应用研究
余 兰,岳建平
(河海大学地球科学与工程学院,江苏南京 211100)
针对BP小波神经网络模型易陷入局部极小和收敛速度慢等问题,结合Morlet小波函数、训练样本数量进行权值和阈值设置,引进隐含层饱和度并构建新的误差函数,以此提高模型收敛速度和预测效果。从模型精度、后验差比值和训练次数这三个指标进行对比分析。结果表明,改进的模型预测效果更满意。
沉陷预测;小波神经网络;模型精度;后验差比值;训练次数
由于开采煤炭给矿区和周旁地表造成裂缝、塌陷、滑坡等地质灾害,同时对经济建设和人民生命财产安全产生不可估量的影响。因此,进行开采沉降监测和预报显得很有现实意义。
对此,近年来,国内外学者进行了大量的研究,如时间序列分析法、灰色理论、Kalman滤波、神经网络等[1]。时间序列分析法只分析时间影响因素,不分析外界影响因素,若外界因素改变,会使得偏差很明显。灰色模型在序列数据迅速改变时,得到的参数值的滞后误差会偏大,使得模型偏差较大。Kalman滤波需要建立精确的数学模型,并具有噪声因子的概率性质,计算精度低,且易发散失效。神经网络不需精确的数学模型,只需无误的学习样本,过量的噪声样本必会使学习结果出错,以致神经网络无效。针对上述问题,建立了改进模型,将改进的小波分析方法和神经网络理论进行有机结合,突显小波变换独有的时频局域化和神经网络超强的自学习能力,进而提高模型精度和预测效果[2]。
1 BP小波神经网络模型的建模过程
建立的改进模型是将小波变换独有的时频局域化特性和神经网络超强的自学习能力进行嵌套结合,该网络是对权值训练的非线性可微函数的多层前向网络,其算法基于误差反向传播[3,4]。
1.1 BP小波神经网络结构
三层神经网络模型的拓扑结构含输入层、隐含层和输出层,其结构如图1所示。在该网络中,用小波函数替代隐含层函数,用小波基函数的尺度和平移参数替代输入层和隐含层之间的权值和阈值[5,6]。
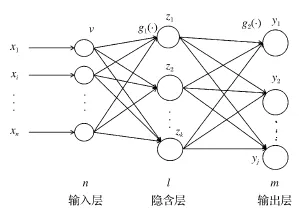
图1 BP神经网络模型Fig.1 BP neural network model
图1中xi为输入层的输入因子;yj为输出层的输出因子;g1(·)为隐含层传递函数;g2(·)为输出层传递函数;vik为输入层与隐含层的相应节点间连接权值;wkj为隐含层与输出层的相应节点间连接权值。下标i、j、k分别表示输入层、输出层和隐含
1.2 BP小波神经网络误差函数
在此网络中共输入P个训练样本,用x1,x2,…,xp表示,若输入第p个样本后,得到的输出为构建平方型误差函数,第p个样本误差Ep的计算公式为
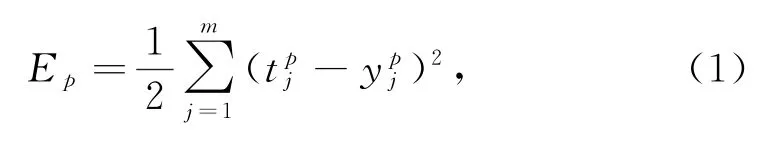
于是,全部训练样本全局误差为
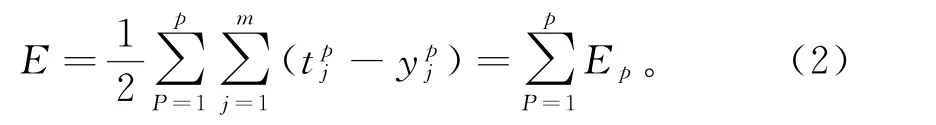
1.3 隐含层和输出层权值设置
(1)输出层权值 对输出层权值wjk用累计误差BP算法调整,可减小全局误差E,即
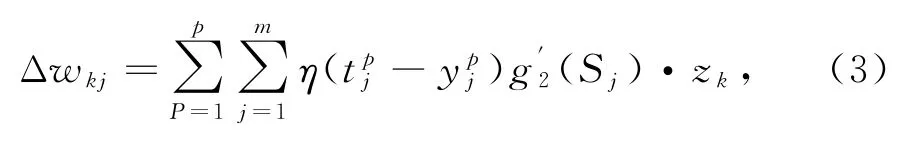
其中:η为学习率,取0~1之间的数为输出层传递函数的偏微分;Sj为第j个神经元净输入值。
(2)隐含层权值 隐含层权值为
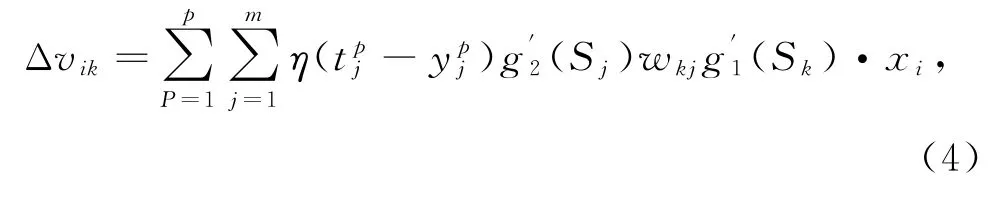
因小波函数的定义域内有大量导数等于零的点,且在这些导数等于零的点的两侧导数有正有负,使该网络的训练速度受到影响,且使训练陷入局部最小[7]。
2 改进的BP小波神经网络
2.1 网络初始参数的选择方法
因神经网络的逼近和收敛能力与初始参数的选择有关,于是结合小波类型、时频参数和训练样本数量设置初始参数,达到小波神经网络的逼近和收敛能力的提高[8,9]。选用的小波函数为Morlet,其表达式为

(1)设置输入层到隐含层权值wki
①wki初始值为随机产生在[-1,1]区间上的均匀分布随机数;
②对wki逐一归一化:
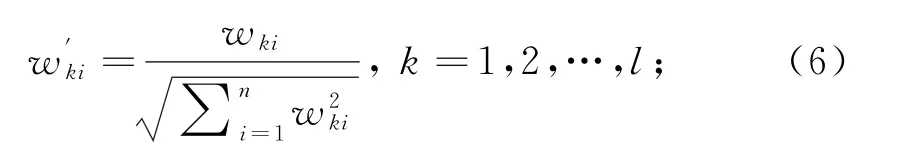
③乘以和隐含层节点数l、输入层节点数n以及传递函数相关联的因子:
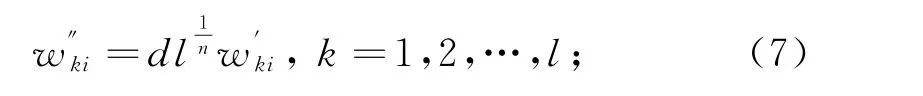
其中:d为传递函数相关联的因子,通过多次学习和实践可知Morlet小波比较合适的值为2.3~2.6[7]。
④建立与学习样本关系。设在输入层第i个神经元中样本最大值是ximax,最小值是ximin,于是有:
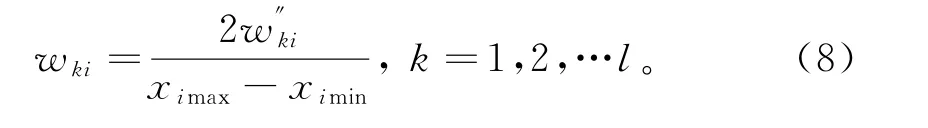
经过上述4步后得出输入层与隐含层间初始权值wki。
(2)设置隐含层神经元阈值θk
①θk初始值为随机产生在[-1,1]区间上均匀分布的随机数;
②乘以和隐含层节点数l、输入层节点数n以及传递函数相关联的因子:

③建立学习样本以及wki关系:
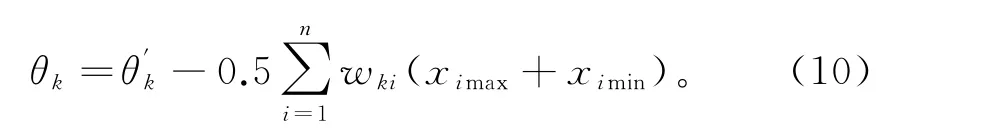
(3)小波伸缩平移参数的设置 假设小波时域中心为t∗,半径为Δt,则小波伸缩系区域在时域中区间为[b+at∗-aΔt,b+at∗+aΔt]。
为让小波伸缩系包含在全部输入向量范畴内,必须设置伸缩平移参数,其表达式为
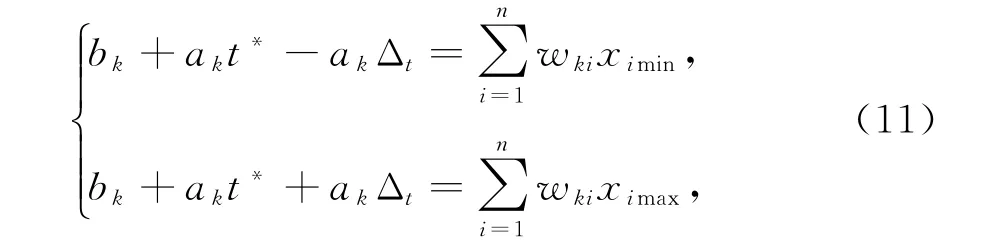
由式(11)可解得
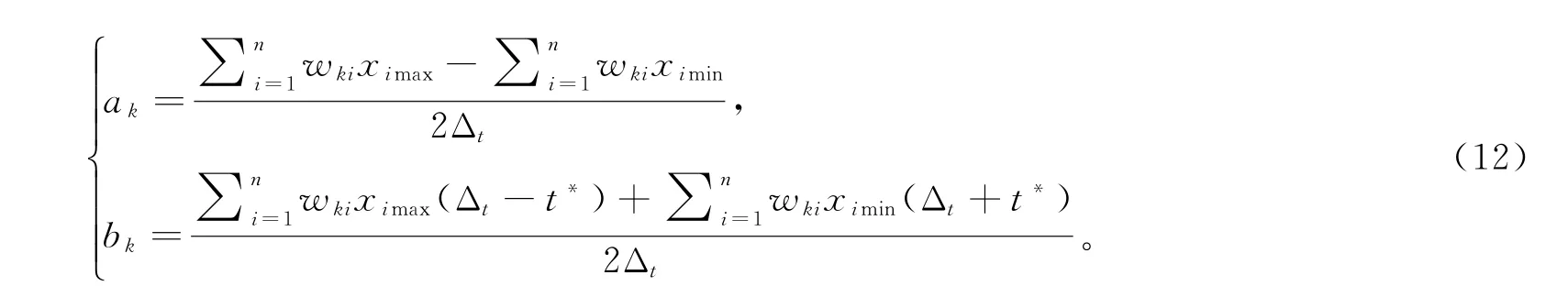
再基于小波时频参数的定义,计算出Morlet小波的时域中心t∗=0,半径Δt=0.707 1。对于隐含层与输出层间初始权值和阈值为均匀分布在[-1, 1]上的随机数,输出层多数情况下为线性神经元。
2.2 网络学习方法
误差函数通过标准的BP算法只计算了输出层实际与期望输出之差的平方和,没有将隐含层神经元考虑。因为隐含层神经元处在饱和状态下,就不再进行网络学习,从而使得BP算法陷进局部极小。针对此问题,通过引进隐含层饱和度以此构建新的误差函数,仍进行梯度下降法计算,使得实际和期望输出相近,从而使隐含层饱和度降低,并解决局部极小问题[10,11]。
新的误差函数为
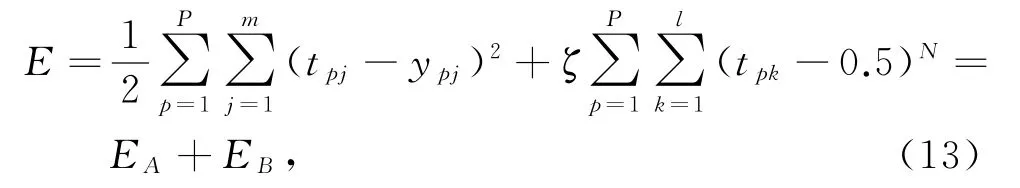
其中:P为全部输入样本数;xp为第p个样本输入向量;tp为期望输出;yp为实际输出;Op为隐含层实际输出;ζ为隐含层饱和度比例因子。通过引进隐层饱和度到新误差函数中,可同步使得EA、EB极小,以防隐含层和输出层神经元达到饱和。此外,EB对EA还具有双重控制作用,当EA较大时,可使EB达到极小,EB可以适当减弱隐层饱和度陷入局部极小,当EA较小时,可减小ζ或者增大N(N必须是偶数),从而减弱EB对网络的影响,可以有效避免训练振荡,使BP算法收敛速度加快。
3 实例分析
为研究某矿区沉陷发展趋势,选取观测断面某个监测点17期监测数据,利用前12期实测数据xi(i=1,2,…,12)作为训练样本,分为6组,(xi,xi+1,…,xi+6)为第i组,每组中前6个值作为输入节点的输入,后一个作为输出节点的目标值。利用BP小波神经网络、改进后的BP小波神经网络,对后5期累计沉降量进行预测,并和实测值对比分析。
该监测点建模后的预测结果如表1所列。从后验差比值、模型精度和训练次数指标分析改进的BP小波神经网络模型的优越性。改进后的模型后验差比值为0.2,明显小于BP小波神经网络模型后验差比值0.9,即改进模型的残差方差更小,预测值和实测值相比较不离散。改进的模型精度为7.5,与BP小波神经网络模型精度24.4相比,得到明显的提高。改进模型训练次数为752,与BP小波神经网络模型训练次数1 273相比,收敛速度明显加快。
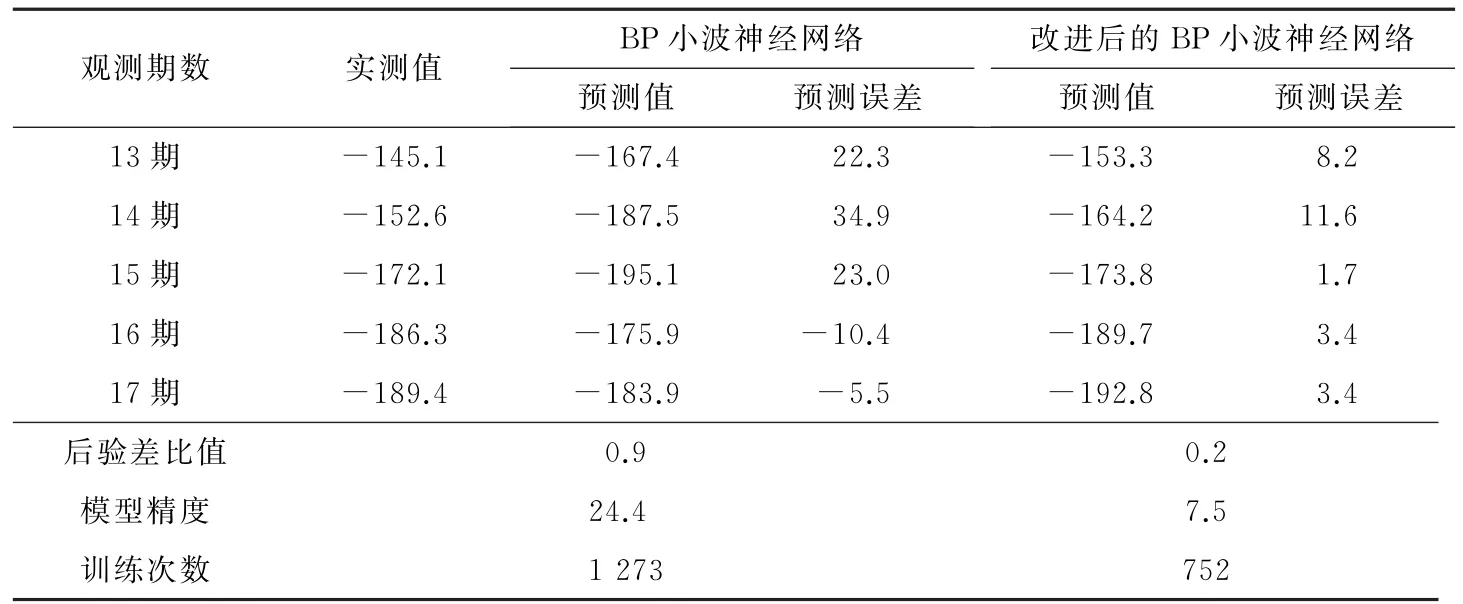
表1 监测点预测结果Table 1 Predicting result in monitoring spot mm
监测点预测误差曲线见图2。由图2可以看出用“bd-”标志的改进的BP小波神经网络拟合误差比用“k∗-”标志的BP小波神经网络拟合误差小很多,改进模型预测误差减小且波动不大。预测结果见图3。图3中用“r∗-”标志的为改进的BP小波神经网络模型的预测累积沉降量,相对于用“b×-”标志的BP神经网络模型的预测累积沉降量,更逼近于用“gd-”标志的实测累积沉降量,从而表明改进后的BP小波神经网络模型预测效果更好。
该实例表明对初始参数和网络学习算法的改进,提高了模型的预测精度,并加快了模型的收敛速度,能很好的在其他工程沉降预测中得到推广应用。
4 结论
针对BP小波神经网络模型易陷入局部极小和收敛速度慢的问题,结合Morlet小波函数、训练样本数量进行了权值和阈值的设置,并引进隐含层饱和度构建新的误差函数,建立改进的BP小波神经网络模型。将改进模型应用于矿区单个监测点预测中,运用模型精度、后验差比值和训练次数指标进行对比分析。结果表明,改进后的模型收敛速度快,预测效果更好。
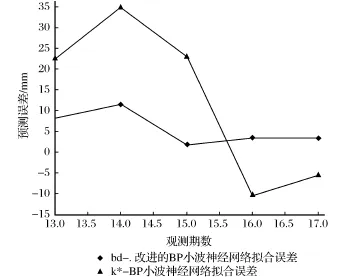
图2 监测点预测误差曲线Fig.2 Predicting error curve of monitoring spot
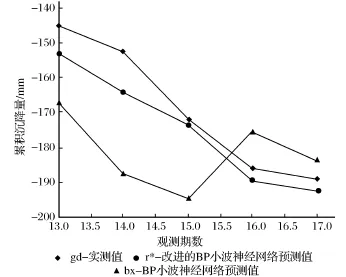
图3 预测结果比较Fig.3 Comparison of predicting result
[1] 王雪英.基于BP神经网络的山区开采沉陷预计[D].太原:太原理工大学,2010.
[2] 魏建.小波人工神经网络在建筑沉降预测中的应用研究[D].北京:北京交通大学,2013.
[3] 关顺,王振伟,张黎.改进遗传神经网络对露天矿边坡位移预测[J].辽宁工程技术大学学报:自然科学版,2015,34(5):619-621.
[4] 杨雪超,何彩平.基于BP人工神经网络的路基压实度预测模型研究[J].甘肃科学学报,2011,23(3):133-135.
[5] 邓勇,张冠宇,李宗春,等.遗传小波神经网络在变形预报中的应用[J].测绘科学,2012,37(5):184-185.
[6] 潘玉明,邓永红,张全柱.小波神经网络模型的确定性预测及应用[J].计算机应用,2013,33(4):1 001-1 004.
[7] 蔡东健,岳建平,成微,等.基于遗传算法的小波神经网络模型及其在地面沉降监控中的应用[J].测绘通报,2010,56(8): 34-35.
[8] 岳荣花.小波神经网络在沉降预测中的应用研究[D].南京:河海大学,2007.
[9] 赵学智,邹春华,陈统坚,等.小波神经网络的参数初始化研究[J].华南理工大学学报:自然科学版,2003,47(2):77-79.
[10] Zhang Qinghua,Benveniste Albert.Wavelet Networks[J].IEEE,Trans on Neural Networks,1992,3(6):889-898.
[11] 胡上尉,孙琼荪,刘佳璐,等.基于修改误差函数新的BP学习算法[J].系统仿真学报,2007,19(19):4 592-4 593.
The Applied Research About Improved BP Wavelet Neural Network Prediction Model
Yu Lan,Yue Jianping
(School of Earth Sciences and Engineering,Hohai University,Nanjing211100,China)
Aiming at the problem often faced with by BP Wavelet neural network model that local is minimum and rate of convergence is slow and combining with that Morlet Wavelet function and training sample number are set weight and threshold value,hidden layer saturability is used to build new error function so that the model rate of convergence and predicting effect can be improved.By comparing model precision,a posterior difference ratio and training frequency,the result shows that the result of improved model is satisfactory.
Sink prediction;Wavelet neural network;Model precision;A posterior difference ratio;Training frequency
P224.2
:A
:1004-0366(2016)05-0038-04
Yu Lan,Yue Jianping.The Applied Research About Improved BP Wavelet Neural Network Prediction Model[J].Journal of Gansu Sciences,2016,28(5):38-41.[余兰,岳建平.改进的BP小波神经网络预测模型应用研究[J].甘肃科学学报,2016,28(5):38-41.]
10.16468/j.cnkii.ssn1004-0366.2016.05.010.层各节点;l、m、n分别表示隐含层、输出层和输入层各节点的数量。
2015-09-28;
:2015-10-27.
余兰(1992-),女,安徽安庆人,硕士,研究方向为变形监测数据处理.E-mail:hohaiyulan@163.com.

