软土地区深基坑工程施工动态风险的概率分析

钱劲斗，郭 健，殷 俊，何章津，柯晓峰

(武汉轻工大学 土木工程与建筑学院，湖北 武汉 430023)

软土地区深基坑工程施工动态风险的概率分析

钱劲斗，郭 健，殷 俊，何章津，柯晓峰

(武汉轻工大学 土木工程与建筑学院，湖北 武汉 430023)

地铁车站深基坑施工风险多、难度大，施工环境及地质条件复杂多变，必然会引起地下土体诱发基坑坍塌等事故的发生。基于基坑变形监测数据，进行基坑安全施工的全过程研究，探讨基坑的变形规律，分析不同工况下基坑风险演变过程。采用三角模糊数学方法探究风险因素，建立不同预警条件下的风险模糊概率。分析不同监测项目之间的相关性，确定各监测项目的影响权重，依据施工阶段各监测项目的风险概率指标，确定基坑的风险等级。工程实例表明，该方法可为深基坑施工环境风险评价提供科学的依据。

基坑工程；施工风险；三角模糊数学；风险评估

1 引言

随着我国日益蓬勃的城市化发展，地铁工程作为缓解城市交通压力的手段之一受到了国内外的一致认可。由于地铁车站多处于城市的繁华地区，周边建筑物分布密集，地下情况错综复杂，因此给车站基坑安全施工带来了极大的难度。所以，加强基坑工程施工的风险管理工作，提前发现隐患，及时处理，从而保证基坑的安全施工显得尤为重要。

由于国内外对于深基坑风险管理的研究尚处于萌芽阶段，大部分的研究都基于定性分析。随着模糊数学的不断发展成熟，越来越多的学者通过建立模糊评价模型实现施工风险的定量分析研究。例如：侯艳娟等运用模糊理论进行风险评估，在分析计算建筑物倾斜及破坏程度的基础上，确定了建筑物的破坏等级[1]；包小华等通过应用模糊综合评价法[2]，构造了基坑风险判断矩阵，定量计算了基坑的风险等级；张弛等以模糊数学为理论基础建立了基坑地表沉降对周边环境影响的分析模型[3]，确定了周边建筑物、道路及管线的破坏等级。由于国内缺乏完整且全面的施工事故统计资料，因此难以通过统计的方法科学准确地确定风险事故损失及发生概率，需要借助一定的专家经验进行定性分析评估，在专家经验不足的情况下，很容易造成评估结果随机性和主观性过大的问题，从而导致评价结果不准确。随着深基坑工程安全监测日益受到重视，国内外学者越来越青睐于研究监测数据反应基坑变形、受力和位移的内在规律以及基坑的风险状况，但多数学者更善于通过数值模拟软件建立预测变形研究模型，并对比监测数据分析验证模型的有效性，从而提出相对应的建议，很少有学者能通过研究监测数据、采用数据挖掘的方式分析基坑每日的风险变化过程。例如：周勇、魏蒿锜[4]等人以兰州地铁某车站基坑为背景，通过有限元数值模拟及实际监测数据的对比分析，表明了基坑开挖及降水对地下管线沉降的影响，并总结了管道的变形规律；俞建霖、厦霄[5]等人借助Plaxis软件模拟基坑施工过程中围护结构的变形情况，并与监测数据对比分析，讨论了坑外土体位移的变形规律；陈昆、闫澍旺[6]通过对天津某大型基坑开挖过程中围护结构及坑外土体的变形情况进行全过程监测，并利用有限元软件建立三维基坑同时开挖过程中邻近位置围护墙变形、支撑轴力和立柱沉降受到的影响。由于基坑施工风险状况与基坑开挖过程有着密切的联系，风险等级会随着开挖深度不断提高，而监测数据是最能反映基坑风险演变规律的第一手数据资料。但基坑安全监测项目的测点众多，且测点的累计变化量及变化速率各有差异，反映基坑的安全水平各有千秋，因此整合所有的测点数据，并对其进行统一分析研究，从整体上把控基坑的风险水平变化，并通过超标的累计变化量分析造成此现象的施工因素，具有重要意义。

笔者在本车站基坑大量监测数据统计分析的基础上，采用比值法将不同纲量的监测数据进行归纳总结，借助三角模糊数学确定了各监测项目指标可能造成基坑破坏的概率，通过层次分析法计算监测项目之间的权重向量，并最终确定了此车站基坑的风险水平演变规律。通过对比分析，所确定的风险水平与实际相吻合。

2 地铁站基坑工程

2.1 工程概况

厦门某地铁站为地下二层岛式车站 ，双柱三跨闭合框架结构。标准段底板埋深16.61―17 m，宽度21.9 m；端头井底板埋深18 m，宽度25.8 m。采用半幅盖挖法施工。基坑采用地下连续墙+内支撑体系，主体围护结构采用800 mm地下连续墙，竖向设置4道内支撑，第一道为钢筋混凝土支撑，其余三道支撑为φ609，t=16 mm的钢管支撑。

2.2 工程地质条件

本车站范围内覆盖层主要为第四系人工填土层、第四系残积砾质黏性土层；下伏基岩主要为燕山晚期侵入岩——中粗粒花岗岩，其中不均匀穿插辉绿岩脉，受区域地质构造和风化作用影响，岩石风化不均匀，中等—微风化基岩面起伏较大。

2.3 水文地质条件

场区地表水不发育。按赋存介质，地下水可为三类：松散岩类孔隙水，孔隙裂隙水以及基岩裂隙水。场区松散岩类孔隙水、基岩裂隙水及风化残疾 岩孔隙裂隙水均直接或间接靠大气降水补给，但补给程度有一定差异。出露高程较大的裸露基岩区完全接受大气降水补给，延伸至沟谷洼地及台地覆盖层下的基岩构造带中的裂隙水，由于补给区位置高，地下水多具承压性质。

2.4 监测点布设状况

本车站依据“能直接反映监测对象的位移、变形或受力状态”的原则确定监测项目。将基坑周边3倍开挖深度的区域设定为基坑监测范围，选定地表沉降、建筑物沉降、管线沉降、墙体沉降、墙体水平位移、砼支撑轴力、钢支撑轴力和地下水位等作为反应基坑整体变形的监测项目，测点数量如表1所示。由于各监测项目累计变化量各有差异，因此导致基坑破坏的相对重要性不同，通过统计各监测项目所有测点平均变化量、最大累计变化量，采用层次分析法定性[7]分析确定各项目相互之间的重要性，建立权重矩阵定量计算，结果如表1所示。

表1 监测项目影响权重及测点数量

3 风险发生概率的定量计算

笔者将上述选定的8个监测项目作为反应基坑变形的风险控制指标。为不失一般性，采用三角模糊型函数[8]描述事件的风险概率。如图1所示。

假设某风险事件xi风险状态为ai的模糊概率P(xi=ai)的模糊子集[g-μgl，g，g+μgr]，其中g为模糊子集的中心，μgl和μgr为左右模糊区间界限。由隶属度函数可知，当μgl和μgr取值越小，则风险概率越精确，反之，则模糊化程度高。

3.1 模糊子集的确定

由于基坑同一个监测项目的测点众多，每一个测点的累计变化量不同，反应基坑的风险状况有一定的差异性。考虑到单一的测点累计变化量不足以说明整个工程的风险情况，但工程的风险情况水平依赖于每一个测点的累计变化量。因此，将测点累计变化量反映基坑的故障状态分为三个等级：黄色警报、橙色警报、红色警报，并定义：当累计变化量处于控制值的40%―60%以内属于黄色警报，处于60%―80%属于橙色警报，大于80%属于红色警报，即:V={(40%，60%) (60%，80%) (80%，∝) }。考虑到不同预警等级对基坑的安全影响权重不同，具有一定的模糊性，这里同样采用层次分析法分析计算，两两定性分析相对重要性，结果如表2所示。

表2 预警等级权重表

预警等级权重黄色预警0．26440．22450．1047橙色预警0．73560．38950．2583红色预警0．61050．77550．6370

笔者采用比值法将最大累计变化量单位化[0 1]区间上，即用累计变化量除以控制值作为风险概率，并取最小值作为模糊子集的下限，最大值作为模糊子集的上限，区间均值作为模糊子集的中心值。控制值参考规范[9]确定。由此可见不同故障状态下监测项目指标反应基坑破坏的概率便在此区间滑动。

(1)

3.2 重心法解模糊化

由于上述采用三角模糊集合仅确定了不同预警条件下风险概率的分布区间G，因此我们需要将其转换为一个明确的g*代表此区间，也就是找一个最适合代表模糊集合U(g)的明确点g*∈U(g)。

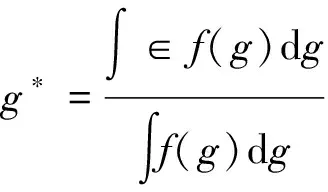
(2)

解模糊化糊化的方法比较多，重心法、形心法、中值法及最大最小集合法都可以实现此过程，其中重心法是最常用的方法，计算结果也最为合理，即采用公式2,求解三角模糊区间模型的重心，如图1所示。

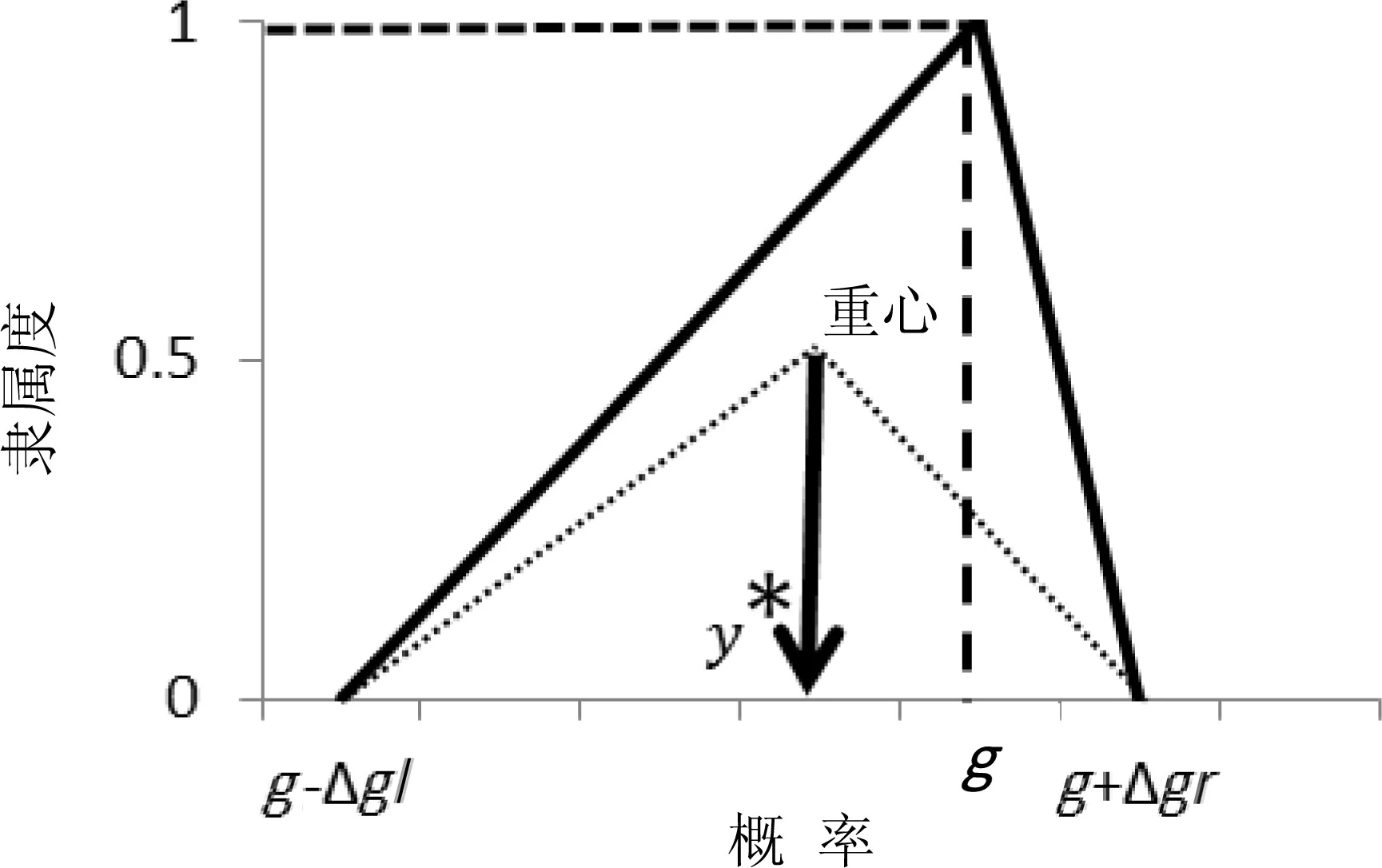
图1 三角模糊函数

4 全过程动态风险概率计算

4.1 基坑开挖施工进度安排

由于本基坑采取分段开挖的方式，为了反应基坑开挖全过程中的风险演变规律，笔者 结合施工进度计算不同工况下各监测项目的风险发生概率，从而达到了各监测项目监测数据与基坑整体安全的同步性。各施工阶段的进度详如表4所示。

4.2 施工过程中监测项目风险概率计算

采用上述三角模糊数学建立各监测项目不同工况下各预警情状态的三角模糊概率区间，通过重心法解模糊化求解模糊概率，并结合之前表2计算所得的预警权重指标，计算每一个监测项目的加权风险概率，计算结果如表5、表6所示。

表3 监测项目累积控制值

监测项目红色预警值/mm橙色预警值/mm黄色预警值/mm累计值变化速率累计值变化速率累计值变化速率地表沉降40—503—530—402—3<30<1建筑物沉降20—30310—202—3<10<1管线沉降10—302—37．5—221—2<15<1墙体沉降20—303—410—201—3<10<1墙体水平位移40—603—520—401—3砼支撑轴力钢支撑轴力(70%—80%)f(60%—70%)f<60%f地下水位1000300—500500—1000100—300<500<100

注：f―构件的承载能力设计值。

表4 施工进度计划

编号日期施工进度计划安排12015⁃07⁃27东区59—60轴基坑开挖，开挖深度约6m22015⁃08⁃13东区55—57开挖深度约6m；56—58开挖深度约12m；59—60段开挖深度约15．5m。……………132016⁃04⁃09东区24—28开挖至16．5m左右；28—32开挖深度约为19．5m；32—60开始浇筑底板及主体结构；西区1—20浇筑底板及主体结构；标准段20—24开挖至19．5m左右。142016⁃04⁃29基坑开挖完成，开始全面浇筑主体结构，部分已进行回填土及路面回复

表5 周边环境风险概率表

进度编号/模糊概率地表沉降建筑物沉降管线沉降地下水位黄色橙色红色黄色橙色红色黄色橙色红色黄色橙色红色1模糊概率0．11200．14670．25500．2950综合概率0．11200．14670．25500．2950………………12模糊概率0．48300．68000．80400．44670．57000．88000．45000．6700综合概率0．73840．44670．615013模糊概率0．48200．62200．47780．48500．93500．40000．6900综合概率0．58700．47780．615714模糊概率0．48200．61000．45830．52000．94000．5886综合概率0．57850．45830．5886

表6 基坑自身风险概率表

进度编号/模糊概率墙体竖向位移墙体水平位移钢支撑轴力砼支撑轴力黄色橙色红色黄色橙色红色黄色橙色红色黄色橙色红色1模糊概率0．19330．11850．4441综合概率0．19330．11850．4441………………12模糊概率0．46000．35170．66770．48850．5342综合概率0．46000．58420．48850．534213模糊概率0．23330．26650．61670．45520．5551综合概率0．23330．52410．45520．555114模糊概率0．21330．46880．44230．5233综合概率0．21330．46880．44230．5233

5 车站整体施工安全状态分析

通过上述计算过程，分别得到了监测项目随施工进度的风险概率值，结合表1分析并通过公式(2)计算所得的各监测项目对基坑安全影响的权重，计算各施工阶段周边环境及基坑自身的加权平均风险概率值，结果如表7所示。

P=∑wi·pi.

(2)

其中P表示监测项目加权后的概率；wi代表各预警状态的权重；pi表示各预警状态的模糊概率。

表7 车站基坑风险概率表

进度/监测项目周边环境风险概率基坑自身风险概率车站整体安全状态风险概率10．21730．17080．198420．32440．30540．320230．39610．51000．460040．48840．55390．529150．54200．65070．605760．60960．65890．644770．69820．67840．700080．66490．59850．642890．60530．57020．5979100．64030．57510．6181110．60210．49420．5579120．63980．50430．5825130．63540．44150．5483140．62500．41140．5277

图2 车站整体安全风险概率水平与周边环境及基坑自身风险概率水平关系变化图

图2分别给出了车站整体安全状态、周边环境和基坑自身风险随施工进度的变化过程。从图2中可以看出：随着基坑的开挖，三者的风险状况会有一个明细的上升趋势，并达到峰值，结合工况信息我们可以判断，基坑开挖已经过半，并开始浇筑主体结构，此时风险情况达到最大值；此后随着部分施工段主体结构的浇筑，虽然基坑仍然在开挖中，但风险水平并未增长。上述信息表明：及时浇筑主体结果对于基坑的施工安全具有重要意义，可以有效地提高施工安全水平，降低事故的发生频率。

图3显示了地表沉降与建筑物及管线沉降随施工进度的变化过程。可以看出：随着地表沉降风险的持续增高，建筑物沉降及管线沉降也在明显增高，而且管线的沉降相比于建筑物沉降更为明显，并且持续上升，但地表沉降和建筑物沉降有下降的趋势，并伴随上下波动。上述变化情况说明：基坑开挖对地下管线的影响较大，因此有必要针对地下管线的沉降做出适当的地表注浆加固等防范措施。

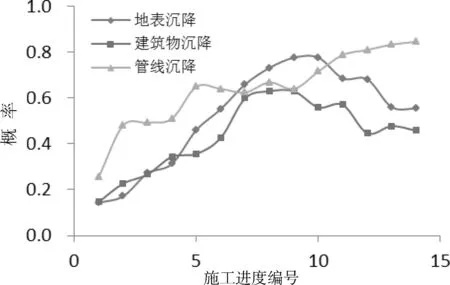
图3 地表沉降风险概率水平与建筑物沉降及管线沉降风险概率水平关系变化图

图4 墙体水平位移风险概率水平与支撑风险概率水平关系变化图

图4描述的是墙体水平位移与支撑轴力的变化关系：在基坑开挖的过程中，三者的变化趋势是一样的，随着深度不断增加，支撑轴力的风险水平将达到峰值，然后逐渐下降，但墙体水平位移会保持一个风险水平并持续一段时间，之后逐渐下降。结果工况分析，造成此趋势的原因主要因为：随着部分标准段主体结构的浇筑，此基坑段的支撑轴力风险会下降，但随着其他开挖段的继续施工，钢支撑架设不及时导致墙体水平位移持续处于高风险，后随着支撑的架设，墙体水平位移的变形逐渐减小。

图5反应了地下水位的变化与地表沉降及墙体水平位移的风险变化关系：三者的变化规律基本一致，因此可以通过地下水位的变化情况，逐步了解地表与墙体水平的变化情况，也可以通过地表沉降的变化规律来分析墙体水平位移的变化情况。由此可知，在某些监测项目失效从而无法表达其风险状态的情况下，可以根据其他相关的监测项目间接的分析其变化情况，从而帮助决策者能全面了解基坑持续施工的风险水平。

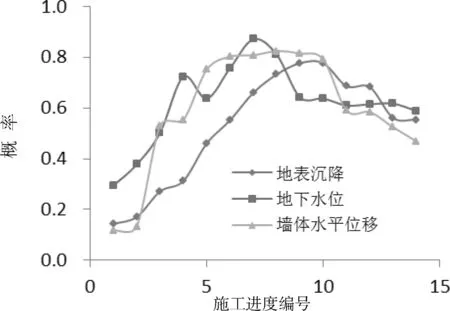
图5 墙体水平位移风险概率水平与地表、地下水位风险概率水平关系变化图

6 结论

笔者基于监测数据分析车站基坑风险变化随开挖深度及施工进度的演变规律。通过上述研究可以得到以下几点结论：

(1)依据基坑变形监测数据，采用模糊数学将所有监测项目的监测数据按预警等级统一分析研究，不仅有效地利用了监测数据反应基坑变形的有效信息，更准确地分析了基坑风险状态的演化规律。结合实践分析，此方法可为类似工程风险管理提供理论经验。

(2)从数据分析结果表明：基坑风险状态会随着基坑开挖深度及施工进度有一个明细的上升趋势并达到峰值，此后风险水平会缓慢下降并伴随上下小幅度的波动。通过对数据和施工信息的研究表明：此变化过程主要是因为部分施工段主体结构的及时浇筑所导致，由此说明，及时浇筑主体结构会有效降低基坑的风险发生。

(3)结合施工工况信息实现基坑风险动态管理的过程，不仅能正确、科学的指导施工，合理安排施工进度，更可以结合单一监测项目的风险变化情况，在其他监测项目失效的情况下，分析其风险变化规律，从而在基坑风险管理的过程中，能全面考虑，将基坑破坏的可能性降至最低水平。

[1] 侯艳娟, 张顶立. 浅埋大跨隧道穿越复杂建筑物安全风险分析及评估[J]. 岩石力学与工程学报, 2007, 26(s2): 3718-3726.

[2] 包小华, 付艳斌, 黄宏伟.深基坑开挖过程中的风险评估及案例分析[J]. 岩土工程学报, 2014,36(s1):193-197.

[3] 张弛, 黄广龙. 深基坑施工环境影响的模糊风险分析[J].岩土力学与工程学报, 2013.32(s1): 2670-2675.

[4] 周勇, 锜魏嵩, 朱彦鹏. 兰州地铁车站深基坑开挖过程中降水对邻近地下管道的影响[J]. 岩土工程学报, 2014,36(s2):496-499.

[5] 俞建霖, 夏霄, 张伟, 等. 砂性土地基深基坑工程对周边环境的影响分析. 岩土工程学报[J], 2014，36(s2):312-318.

[6] 陈昆, 闫澍旺, 孙立强, 等. 开挖卸荷状态下深基坑变形特性研究[J].岩土力学, 2016，37(4):1076-1082.

[7] 望应洛. 系统工程[M]. 北京: 机械工程出版社, 2003.

[8] 胡宝清. 模糊理论基础[M]. 武汉：武汉大学出版社, 2004.

[9] GB 50911-2013 ，城市轨道交通工程监测技术规范[S].

The probability analysis of dynamic risk of deep foundation pit construction in soft soil area

QIAN Jin-dou, GUO Jian, YIN Jun, HE Zhang-jin, KE Xiao-feng

(School of Civil Engineering and Architecture , Wuhan Polytechnic University, Wuhan 430023, China)

The deep excavation in a complex environment would inevitably cause soil deformations，which will induced underground foundation pit collapse accidents happening by deformation of soil. In this paper, by researching the whole process of foundation pit construction safety based on the deformation monitoring data,discusses the deformation regularity and risk level change in the development of foundation pit. Then, utilizes triangle fuzzy mathematics to establish probability interval and calculates the corresponding fuzzy probability. By means of analyzing the correlation between different monitoring items, confirms the effect weight of every factors. At last, through calculating the risk probability of different construction stages of the monitoring project indicators to analyze the risk of foundation pit level evolution regular. The engineering cases showed that the method was a high accuracy and a good prospect for analyzing the characteristics of construction deformation due to deep excavations.

deep excavation;construction deformation;triangle fuzzy mathematics;risk assessment

2016-10-20.

钱劲斗(1990-)，硕士研究生,E-mail：421327303@qq.com.

郭健(1968-)，男，教授，E-mail: guojianxh@163.com.

住建部科学技术项目计划(2015-K3-04)；武汉轻工大学研究生教育教学改革研究与实践项目(YY2015006).

2095-7386(2016)04-0052-06

10.3969/j.issn.2095-7386.2016.04.010

TU 4

A