深厚覆盖层上土石坝应力应变三维仿真分析

代凌辉，闫国新，李建

（1.黄河水利职业技术学院，河南开封475004；2.小流域水利河南省高校工程技术研究中心，河南开封475004）

深厚覆盖层上土石坝应力应变三维仿真分析

代凌辉1，2，闫国新1，2，李建1，2

（1.黄河水利职业技术学院，河南开封475004；2.小流域水利河南省高校工程技术研究中心，河南开封475004）

以有限元方法为基础，对新疆吐鲁番二塘沟水利枢纽工程的土石坝进行了三维仿真计算，并对堆石体和心墙在竣工期和满蓄期的应力应变极值进行了分析。分析结果表明，该土石坝的设计是合理的，堆石体和心墙不会发生拉压破坏或剪切破坏；心墙底部向两侧发生大约7 cm的轻微侧胀，成为比较危险的部位，在设计和施工中应予以高度重视。

新疆吐鲁番二塘沟水利枢纽；土石坝；应力应变；三维仿真；本构模型

0　引言

随着有限元计算技术的发展，土石坝在设计施工和应力应变计算方面也有了比较大的进展。其中，数值仿真是一项比较先进的计算方法。在传统的研究方法中，当结构形式比较特殊，且荷载或材料性质复杂时，可采取模型试验的研究方法。但是，这种方法往往受到客观环境的约束，有时不能够完全反映实际情况。数值仿真计算方法能够进行全尺寸的试验模拟，可以方便地调整参数，还可以通过颜色的深浅给出三维物体中各点力的大小或用不同颜色表示出不同的等力面；也可以任意变换角度，从任意点去观察。这样，就使计算者的思维更加形象化，概念也更易于理解。

在进行数值仿真计算时，三维仿真比二维仿真更具优势［1］。如，在土石坝的计算中，二维仿真一般是按平面应变问题进行考虑的，相当于假设坝体沿坝轴线方向为无限长。但事实上，许多坝体在坝轴线方向并不是很长，如果按平面应变问题来考虑，会忽略两岸山体对坝体的影响，从而造成一定的误差［2］。而三维仿真则是对土石坝建立三维有限元模型，虽然网格和节点数量都大大增加，但是模型更接近真实情况，而且能得到更为丰富的计算结果。

笔者以新疆吐鲁番二塘沟水利枢纽工程深厚覆盖层上的沥青混凝土心墙土石坝工程为例，以Duncan－Chang E－μ材料本构模型和Goodman单元接触模型为基础，进行应力应变的三维仿真计算，分析堆石体和心墙在竣工期和满蓄期两种工况下是否满足安全要求，沿坝轴线方向的应力应变状态，及其发生破坏的可能性。

1　有限元计算的本构模型

在土石坝的有限元计算中，首先要选择一个合适的计算模型，即本构关系。常见的材料本构模型比较多［3］，其中Duncan－Chang E－μ本构模型能够反映土体变形的主要特点，而且理论公式简单，参数物理意义明确，易于获取，成为目前应用最为广泛的本构模型之一［4］。本文将采用该模型进行计算。Duncan－Chang E－μ本构模型的切线弹性模量表达式如式（1）所示［5］。

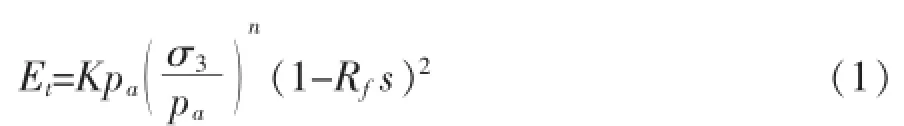
式中：Et为切线弹性模量；pa为单位大气压力；σ3为小主应力；Rf为破坏比；s为应力水平；K、n为模型参数，由常规三轴试验得出。

本文计算时，沥青心墙与过渡料之间、沥青心墙与混凝土基座之间设置接触，采用Goodman单元接触模型。在三维仿真计算中，该接触模型的接触面单元上有两个切线方向的劲度，其表达式如式（2）所示［6］。

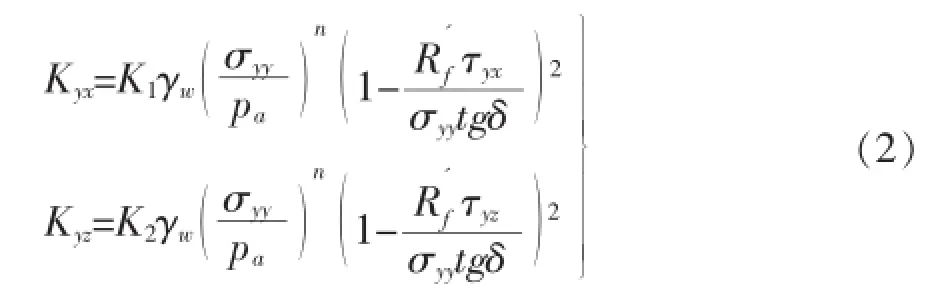
式中：τ为接触面上的剪应力；K1、K2、n、Rf'为模型试验参数；δ为两种接触面材料的摩擦角；σ为主应力；γw为水的容重；pa为单位大气压力；Goodman单元接触模型中的法向劲度系数为Kyy，当接触面受压时，取较大值（如Kyy＝108kN／m3），当接触面受拉时，取较小值（如Kyy＝10 kN／m3）。

2　工程算例

2.1三维仿真模型的建立

新疆二塘沟土石坝为沥青混凝土心墙坝，坝顶高程为1 478.80m，防浪墙高为1.2m，坝顶宽为8.0m，最大坝高为64.30m，坝顶长为337.033m。上游坝坡为1∶2.25，下游坝坡为1∶2.0。河床深厚覆盖层原为64m。大坝防渗体为沥青混凝土垂直心墙，顶宽0.5m，底宽1.2m。心墙上、下游两侧各设3m厚的过渡层。坝基防渗主要采用混凝土防渗墙，防渗墙最大深度为66.0m，厚度为1.0m。坝体总填筑量为220万m3，其中，沥青混凝土心墙总填筑量为1.25万m3，混凝土防渗墙面积为5 500m2。大坝三维仿真模型建模情况为：坝基沿河流方向从上、下游坡脚分别向上游和下游取1倍坝高的长度；坝基向下取至覆盖层与基岩交界处；沿坝轴线方向从坝顶与两岸山体的交界处分别向两岸取30m长的山体，并垂直向下通至与覆盖层底部平齐的高程。模型底部采用固定约束，四周约束水平向自由度。模型共划分了26 600个节点，23 940个单元。其中，沥青混凝土心墙沿厚度方向划分了4层单元，共1 260个单元。三维仿真模型的单元类型主要为八节点六面体线性完全积分单元，有少量的六节点五面体单元。三维仿真模型整体网格如图1所示。

图1　大坝三维仿真模型整体网格图Fig.1 Dam three－dimensional simulation model grid

2.2模型参数

本文在进行仿真计算时，坝壳料、过渡料、坝基沙砾石和沥青混凝土心墙均采用Duncan－ChangE－μ本构模型；混凝土防渗墙采用弹性模型。各种材料的Duncan－ChangE－μ模型参数取值见表1。沥青心墙与过渡料之间、沥青心墙与混凝土基座之间设置接触，采用Goodman单元接触本构模型，各参数取值见表2。混凝土防渗墙采用弹性模型，密度为2.4g／cm3，弹性模量为25.5GPa，泊松比为0.17。山体基岩亦采用弹性模型，密度为2.65g／cm3，弹性模量为32GPa，泊松比为0.21。

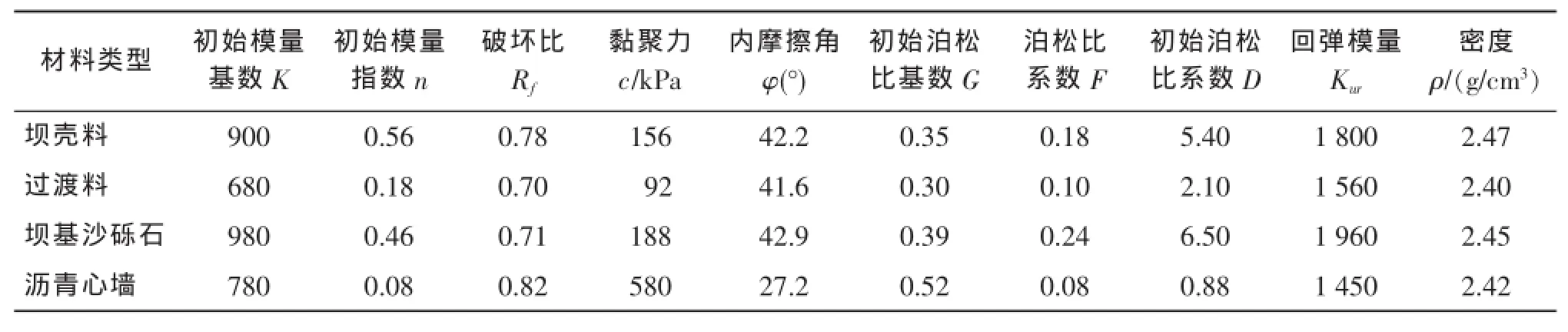
表1　Duncan－Chang E－μ模型参数Tab.1 Duncan－Chang E－μmodel param eters

表2　Goodman单元接触参数Tab.2 Goodm an element contact parameters

2.3地应力平衡

在实际工程中，坝体在填筑之前，坝基内部已经有了应力。所以，在计算时，要先对坝基进行初始地应力平衡，达到坝基内有相应的应力，但是位移为0的目的。地应力平衡效果将影响后续计算结果的正确性，所以它是计算工作中非常重要的一步［7］。本文在进行计算时，采用如下方法进行地应力平衡：（1）将重力荷载施加于坝基，并给予符合工程实际情况的边界条件，计算得到重力荷载下的应力场。（2）通过技术处理，将该应力场定义为初始应力场，在后续计算中，与重力荷载一起施加于原始的有限元模型。该工程地应力平衡之后，坝基各节点的最大水平位移为0.24mm，最大垂直位移为－0.25mm。对于大范围的坝基而言，这个值已经相当小，近似等于0。这说明地应力平衡效果良好。

2.4大坝的填筑加载过程

根据坝体施工分层填筑的实际情况和坝体材料的非线性特性，采用逐级施加荷载的方法，使沥青混凝土心墙与坝壳料、过渡料同步填筑上升［2］。计算模型中的荷载按照坝体施工填筑的先后次序分14级来施加。第1级是对坝基、混凝土防渗墙和两岸山体施加重力荷载；第2～11级是把坝体分十二层逐级加载，包括心墙及上下游过渡料；第12级是对水库蓄水至1 435.83m高程进行加载；第13级是对水库蓄水至1 456.83m高程进行加载；第14级是对水库蓄水至1 476.83m高程进行加载。

3　计算成果分析

提取三维仿真计算结果中竣工期与满蓄期坝体的各物理量极值，具体如表3和表4所示。其中，垂直位移向下为正；沿坝轴线方向水平位移向右岸为负，向左岸为正；顺水流方向水平位移向上游为负，向下游为正；应力和应变受拉为负，受压为正。

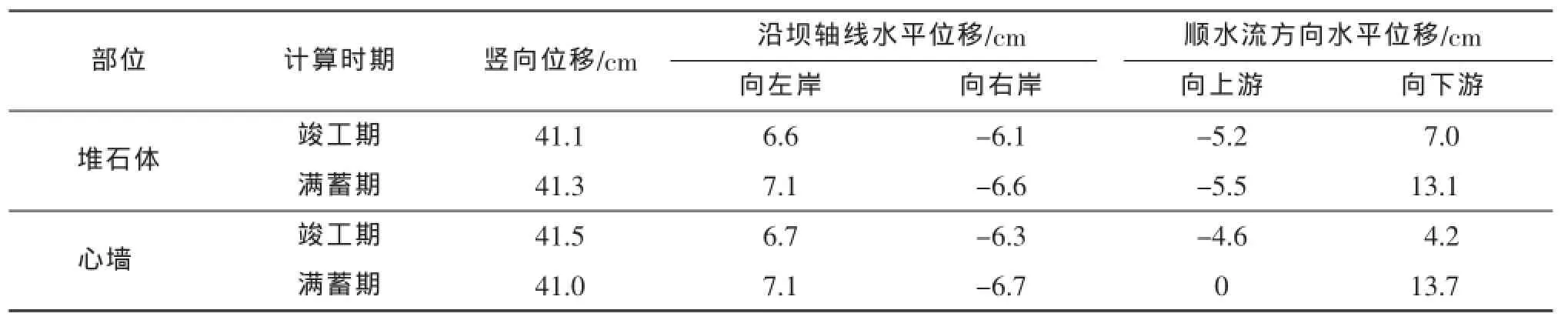
表3　三维模型坝体变形极值Tab.3 Three－dimensional model dam body deformation extreme values

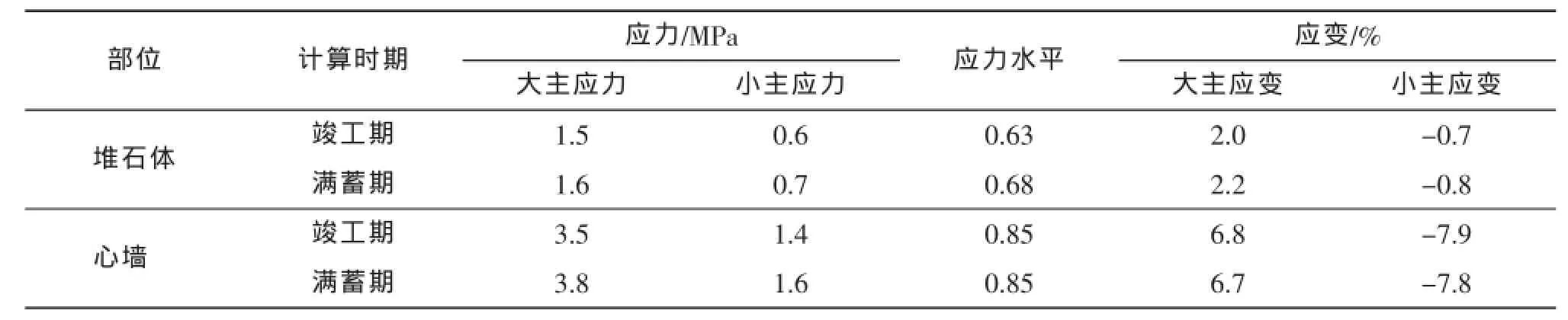
表4　三维模型坝体应力应变极值Tab.4 Three－dimensional model dam body stress－strain extreme values

从表3和表4可以得出，该沥青混凝土心墙坝在竣工期和满蓄期的各物理量极值均在正常水平，满足安全要求。其中，竣工期堆石体应力水平最大值为0.63，心墙应力水平最大值为0.85；满蓄期堆石体应力水平最大值为0.68，心墙应力水平最大值为0.85。以上各应力水平值均小于1，相应部位不会发生破坏。心墙应力水平最大值所发生的位置在心墙底部大约4～5m的高度处，该部位向两侧发生大约7cm左右的轻微侧胀，成为比较危险的部位。满蓄期心墙的应力水平分布情况如图2所示。

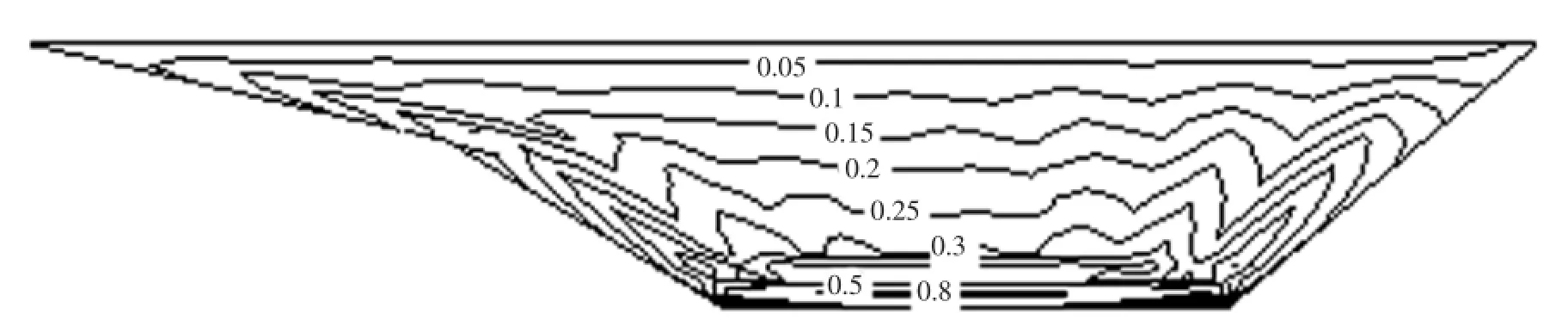
图2　三维仿真模型心墙满蓄期应力水平等值线图Fig.2 The stress level of three－d imensional m odel of core－wall of full storage period

从以上结果分析可以得知，坝体的设计是合理的，堆石体和心墙不会发生拉压或剪切破坏。心墙底部发生侧胀的位置是较危险部位，在设计和施工中应予以高度重视。

4　结语

通过对新疆吐鲁番二塘沟土石坝进行三维仿真计算，得到了堆石体和心墙在竣工期和满蓄期的应力应变极值，并对计算结果进行了分析。结果表明，该土石坝的设计是合理的，堆石体和心墙不会发生拉压或剪切破坏；心墙应力水平最大值发生在心墙底部大约4～5m高度处，该部位向两侧发生大约7 cm左右的轻微侧胀，成为比较危险的部位，在设计和施工中应予以高度重视。

［1］孔宪京，余翔，邹德高.沥青混凝土心墙坝三维有限元静动力分析［J］.大连理工大学学报，2014，54（2）：197－203.

［2］代凌辉.二塘沟水库深厚覆盖层上沥青混凝土心墙坝应力与变形计算分析［D］.乌鲁木齐：新疆农业大学，2011.

［3］沈珠江.土体结构性的数学模型—21世纪土力学的核心问题［J］.岩土工程学报，1996，18（1）：95－97.

［4］李广信.高等土力学［M］.北京：清华大学出版社，2002：50－56.

［5］Goodman R E，Taylor R L，Brekke T L.A Model for the Mechanics of Jointed Rock［J］.Journal of the Soil M echanics and Foundations Division，ASCE，1968，94（3）：637－659.

［6］Duncan JM，Chang Chin－yung.Nonlinear analysis of stress and strain in soils［J］.Journal of the Soil Mechanics and Foundations Division，ASCE，1970，96（5）：1629－1653.

［7］陈卫忠，伍国军，贾善坡.ABAQUS在隧道及地下工程中的应用［M］.北京：中国水利水电出版社，2010：281－342.

[责任编辑杨明庆]

Three－dimensional Simulation Analysis of Earth and Rock fill Dam Stress－strain over Deep Covering Layer

DAI Ling－hui1，2，YAN Guo－xin1，2，LI Jian1，2
（1.Yellow River Conservancy Technical Institute，Kaifeng 475004，Henan，China；2.Engineering Technology Research Center of Henan Province University of Small Watershed Conservancy，Kaifeng 475004，Henan，China）

In this paper，it conducts the three－dimensional simulation calculation on the earth and rockfill dam of Ertanggou hydro－project in Sinkiang Turpan based on the finite element method，and analyzes the stress－strain extreme values of rockfill body and core－wall after the completion period and full storage period.The result shows that the design of the earth and rockfill dam is reasonable，the rockfill body and core－wall won’t appear tension－compression damage and shear failure.At the bottom of the core－wall，it appears about 7cm slight inflation towards to both sides and which makes it become the dangerous place.So we should pay more attention to the design and construction process.

Sinkiang Turpan Ertanggou hydro－project；earth and rockfill dam；stress－strain；threedimensional simulation；constitutive model

TV641

A

1008-486X（2016）02-0008-04

2016-01-06

黄河水利职业技术学院校内科研基金：深厚覆盖层上沥青混凝土心墙坝应力应变仿真分析（2014QNKY013）。

代凌辉（1984-），男，河南开封人，助教，硕士，从事水利工程教学与研究工作。