Excel求解旅行商问题及实现

刘芊

摘要：旅行商问题历来是大家感兴趣的一个难题，对其求解也有各种算法。Excel中规划求解也是有效解决问题的方案之一，通过介绍其基本原理，求解思路和在旅行商问题中的具体实现步骤，希望能对读者学习Excel的高级应用有很好的借鉴作用。

关键词：旅行商问题；规划求解；加载宏

1 引言

旅行商问题（TSP），是假设一个旅行商出于业务需要，要到N个城市去，那么如何找出一条最佳的路径使其能既经过每个城市，又路径最短。旅行商问题在实际工作中有很多具体应用，如货物配送、家用管网规划、网络路由选择等。该类问题与普通的求最短路径的根本区别是：既要经过已知的所有节点，又要从起点到终点形成封闭回路，在满足这两个前提下路径最短。对于较大规模的该类问题，需要通过智能算法（蝙蝠、蚁群等）求解，对于一定规模的旅行商问题可采用Excel的规划求解来解决。

2 方法概述

规划求解是Excel的“可使用加载宏”的一种，它能够对存在多个变量的线性或非线性问题求解，以求出最优值。通过规划求解，可以帮助用户得到最优的设计方案。其工作原理是可以设计多个可调整的单元格，给出这些单元格需遵守的约束条件，同时给出目标单元格的公式，通过改变可变单元格的值，求出目标单元格的最大值、最小值或指定值。

3解决方案：

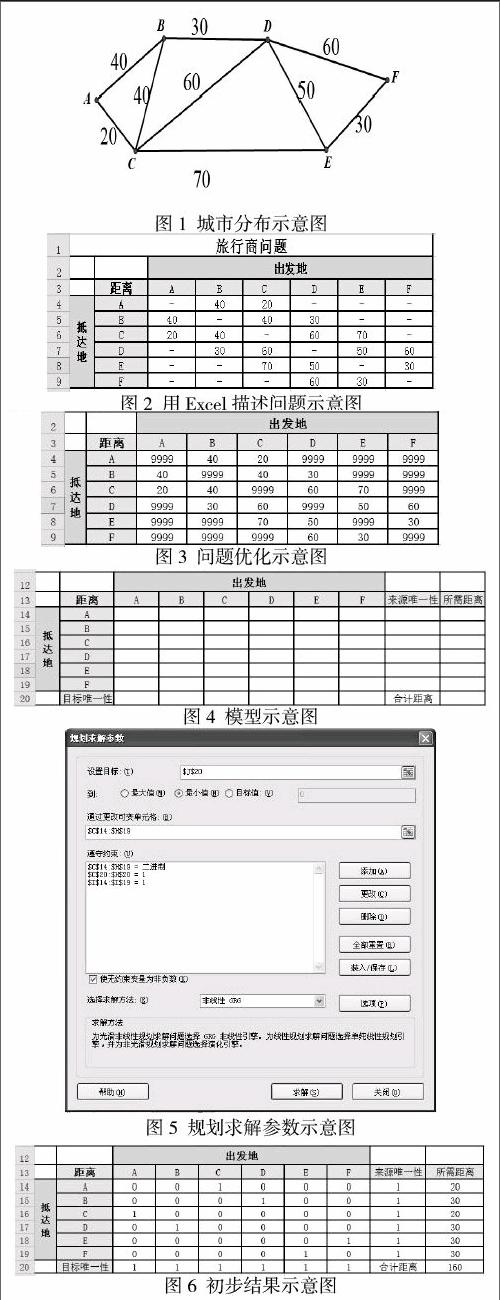
以下图为例，共有A、B、C、D、E、F六个城市，它们之间的路径及距离如图1所示

3.1 打开Excel 2010，建立一个工作簿，名为“旅行商问题”

3.2 在C4：C19单元格，用“9999”来替换“-”，如图所示，该步骤是给不存在的路径用一个很大的数来表示，防止以后选择该路径。

3.3 建立解决模型，如下图所示。

在以上模型中，我们用“来源唯一性”限制出发地，用“目标唯一性”限制抵达地，以确保都任何时候只能走一条路径，不能同时存在多条路径。

打开Excel 2010的“加载宏”选择，选择其中的“规划求解加载项”前的复选框，然后“确定”，操作后我们再打开“数据”选项卡，就能看到“规划求解”。

给单元格输入公式，其中，I14 单元格 =sum（c14：h14），填充I15：I1

C20 单元格=sum（c14：c19），填充D20：H20

J14 单元格 =sumproduct（c4：h4，c14：h14），填充J15：J19

J20 单元格 =sum（j14：j19）

C14：H19 的“单元格格式”我们可以设置为“数字”，选择“自定义”中的“0”，我们用该区域表示实际路径的选择情况，选择即为“1”，不选即为“0”，然后对应出发地、抵达地，形成一条回路。这个区域是可变区域，代表了不同路径的组合可能，J20是规划求解的目标单元格，即总路径，在这里，根据题意我们给J20选“最小值”。

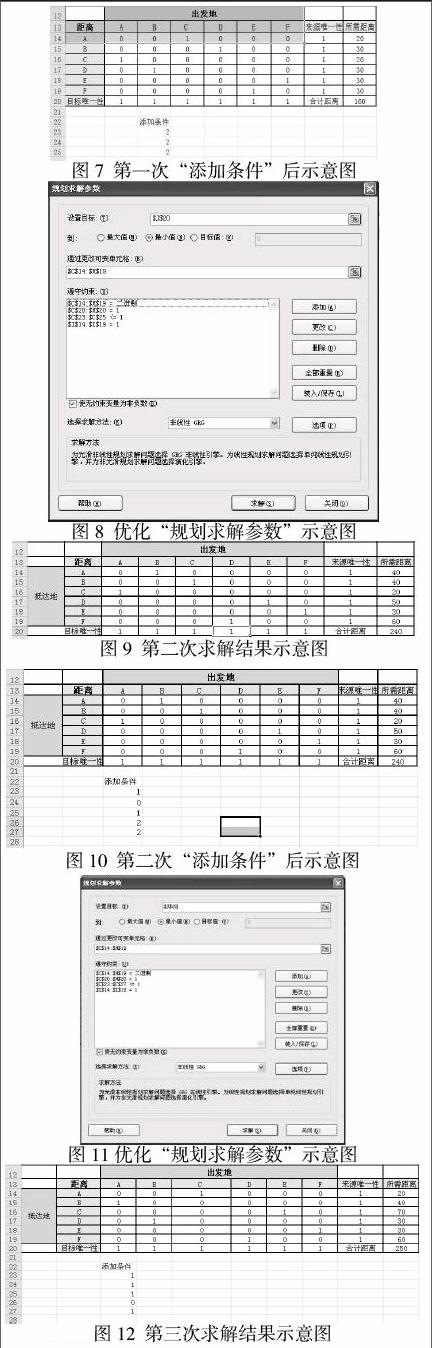
3.4 观察求解结果，可以看到，选择的路径是：C-A-C，B-D-B，E-F-E，它们不能形成封闭回路，所以不符合要求，为解决这个问题，我们需要加上限制条件，防止返回情况发生，也就是E14和C16不能同时为“1”，F15和D17不能同时为“1”，H18和G19不能同时为“1”

在下面可选C23：C25输入这些“添加条件”，C22单元格录入“添加条件”，C23至 C25录入公式。

C23单元格 =E14+C16

C24单元格 =F15+D17

C25单元格 =H18+G19

3.5 继续规划求解，可以在“规划求解参数”对话框中增加约束条件，设置C23：C25<=1

3.6 得出新的规划求解结果，如下图所示。

3.7 经观察，这次求得路径为B-A-C-B，D-F-E-D，仍让没有形成闭合回路，那就要同上增加新的约束条件，C26单元格=D14+E15，C27单元格=F19+G17，

3.8 然后重新设计“规划参数”，如下图所示。

3.9 得出最优的规划求解结果，如下图所示。

3.10 观察下，这次形成的路径是B-D-F-E-C-A-B，为封闭路径，符合要求，那么旅行商路径即为B-D-F-E-C-A-B，反向路径B-A-C-E-F-D-B 也是旅行商的解，路径长同为250。

4 结束语

用Excel2010求解旅行商问题及实现如上分析，具体节点数不同，数据不同，求解过程会有差异，但总体思路是一致的，根据具体路线，有繁有简，实现的步骤也会略有差异。

参考文献：

[1]金晓龙. Excel高级应用实例教程，2012第一版：144-150