干旱区棉田土壤含水率时空变异研究

廉 娟

(新疆塔里木河流域管理局信息中心，新疆 库尔勒 841000)

干旱区棉田土壤含水率时空变异研究

廉 娟

(新疆塔里木河流域管理局信息中心，新疆 库尔勒 841000)

土壤含水率是陆地表层系统的重要变量,广泛影响各种水文循环过程。研究土壤含水率的空间变异特性有助于了解上述循环过程,为制定精准灌溉制度提供依据。本文结合传统统计学与地统计学方法,分析了土壤含水率空间变异特性的时间变化规律及其与土壤平均含水量之间的关系。结果表明:棉田土壤含水率变程较大,且表层土壤含水率的变程大于深层土壤;干旱年份的表层土壤和较湿润年份的表层以下土壤含水率与其他情况下土壤含水率相比,空间结构性变异相对随机性变异的比例高,且随机性相对结构性变异的比例随平均含水率的增加而增加。研究结果为制定合理、精确的农业灌溉管理措施提供了参考。

土壤含水率;棉田;空间变异;地统计学;干旱区

土壤含水率作为陆地表层系统的重要状态变量，在很大程度上影响着田间水分小循环(如土壤侵蚀、溶质运移、植物生长等)及区域水文大循环(如径流、气候变化等)过程［1］，也是水文模型中重要的参数之一。然而，由于自然条件下，土壤性质普遍具有空间变异性，不可避免地土壤含水率在空间上也具有高度的变异特性［2］，研究该特性对分析并准确模拟上述水分循环过程以及优化农业生产活动等具有重要意义［3］。

许多研究者对不同尺度下土壤含水率的空间变异特征及其影响因素进行了研究，结果表明地形、土壤质地、植被等对土壤含水率的空间分布都具有一定的影响［4，5］，而土壤含水率的空间分布常具有一定的时间稳定性。已有的研究多是基于年内的监测数据进行的，少有涉及到土壤含水率空间变异特性的年际变化，同时多数是针对表层土壤进行的研究，着重说明土壤水分水平向的分布特征。另外现有的研究对象多为裸土或草地，植被的影响程度相对农田来说较小。而在农业生产中，作物的根系及灌溉、耕作等农业管理措施会更大程度地影响相对深层土壤的含水率分布变化情况。因此，在农田条件下，综合考虑表层和较深层土壤的含水率空间分布情况及这种分布在年际间的变化规律，对于评价现有管理措施的效果及改进现有措施十分必要。同时在西北半干旱地区，灌溉在农业的可持续发展中占据重要位置。它在很大程度上影响着蒸发蒸腾、根系吸水以及水分横向流动等土壤水分运动过程，从而影响土壤含水率的时空变异。了解灌溉条件下土壤含水率空间结构及其与土壤质地、地形之间的关系可以为制定合理的灌溉措施提供有利信息。鉴于此，本文通过分析干旱区棉田不同深度土壤含水率的3年全生育期监测数据，获得田间尺度上土壤含水率在生育期内的时空变异特征及其在不同年份之间的变化规律，从而为更准确地评估土壤含水率的分布规律以及制定更合理、精确的灌溉管理措施提供参考。

1 材料与方法

1.1 研究区概况

研究区位于新疆尉犁县，该地区属于典型的温带大陆性干旱气候，具有冬冷夏热、干燥、多风的特点。日照充足，光热资源丰富，全年日照时数达3000h以上，平均气温 11.5℃，年积温(＞0℃) 5000℃以上，无霜期约180d。水资源短缺，多年平均降水量 50m m，多年平均蒸发皿蒸发量约2200m m，地下水位在30m以下。

1.2 数据采集

采样点采取均匀网格布置，间距为25m×25m，共12行、12列，共144个采样点。其中，2012年的监测数据来自于均匀分布的135个采样点，2013和2014年的监测数据则包含了所有144个采样点。各采样点测定的体积含水率均通过烘干法测定的质量含水率进行校正。

1.3 数据分析方法

本文利用变异函数描述土壤含水率的空间分布。变异函数是地统计学的基础，用来表征随机变量的空间变异结构或空间连续性。样本变异函数可通过式(1)计算［6，7］:

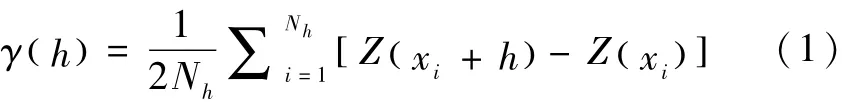
式中:h—分离距离，m;γ(h)—分离距离为h的样本变异函数值;Nh—在(xi+h，xi)之间用来计算距离为h时的样本变异函数值的样本对数;Z(xi+h)，Z(xi)—在位置xi+h与xi处测量的变量值(在本研究中即土壤含水率)。

为了便于分析，一般需要将没有确定函数形式的理论变异函数与经验的变异函数模型进行拟合，并选取拟合效果最好的模型模拟函数特征值进行研究。常用的变异函数模型有球形模型、指数模型、高斯模型3种，其中指数模型的表达式如下［8，9］:

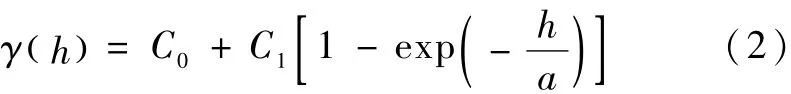
式中:C0—块金值，即在极短样本距离之间变异函数从原点的跳升值，表示取样误差或小于取样距离情况下的空间变异;C1—局部顶值，表示基台值减去C0的值;α—变程，半方差随着样本点间距的增加而增大，并在变程处达到一个基本稳定的常数(基台值);其他变量含义同前。

土壤含水率样本的空间相关程度采用块金效应来评价:

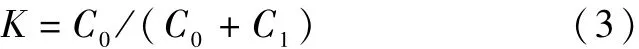
式中:(C0+C1)—基台值，即变异函数所能达到的最大值，表示现有尺度下变量的总体空间差异程度;C0/(C0+C1)—块金效应，Ca m ba r de l l a等将其定义为空间相关度，用来表示样本变量的空间相相关度，且分别以空间相关度≤25%、25%＜空间相关度≤75%、空间相关度＞75%表示强、中等、弱空间相关性。

2 结果与分析

2.1 剖面土壤含水率空间结构随时间变化特征

利用式(1)计算各次采样所得土壤含水率的样本变异函数，并采用上述3种模型进行拟合，选取拟合效果最好的球形模型分析土壤含水率的空间变异特征与规律。图1为2012年5月0～20c m土层、2013年 7月 20～40c m土层、2014年9月 40～60c m土层含水率的样本变异函数及球形模型拟合曲线，代表土壤深度由浅变深时的一般变化情况。不同时间所测土壤含水率的样本变异函数与图1类似。

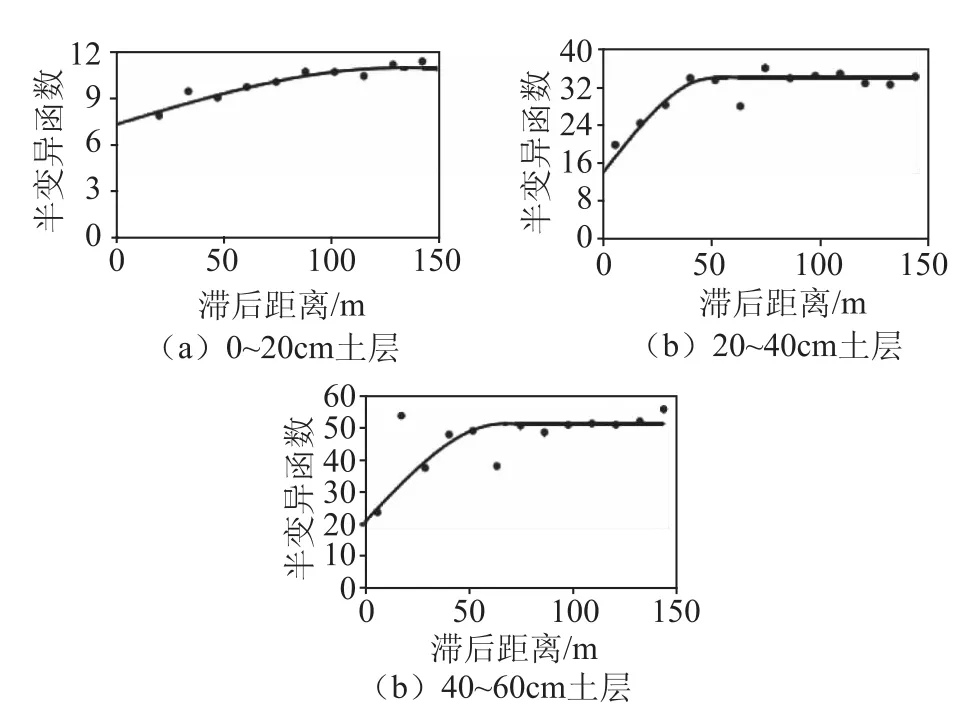
图1 土壤含水率半方差

可以看出，变异函数模型的变程在表层(0～20c m)土壤会比较大。需要指出的是由于2012年的数据缺乏较近距离的采样，变异函数模型中的空间相关度估计值可能存在较大误差，因此本文中针对空间相关度着重比较2013和2014年。

对比同年不同深度土壤含水率变异模型的拟合参数(见表1)，可以看出变程和空间相关度随深度的变化规律在不同年份也不尽相同。2012和2014年，0～20c m土层含水率的变程大小及其变化幅度都明显大于40～60c m土层。2012年0～20c m土层含水率的平均变程约为150m，变化范围为77.71～224.81m，同年40～60c m土层含水率的平均变程则相对较小，仅约为 64m，变化范围为37.18～82.85m;2014年，0～20和40～60c m土层的平均变程与2012年类似，分别约为160和60m。2013年，0～20和 20～40c m的变程相近(约 55m)，40～60c m土层的变程最大，约为 80m。同时，2012和2014年的最大变程分别在20～40和0～20c m土层。上述结果表明，变程随土壤深度(0～60c m)的变化规律与生育期的累积降雨量密切相关:降雨量较大的年份(2012和2014年)，变程在0～40c m随土壤深度增加而减少;降雨量较少的年份(2013年)，土壤含水率变程在表层0～20和20～40c m处类似，且相对40～60c m较小;另外20～60c m土层中变程在2012和2014年呈现不同的趋势，年降雨量接近平均降雨量时(2012年)，土壤含水率的变程随土壤深度增加呈不断减小的趋势，而在降雨量较大的2014年，20～40和40～60c m的变程比较接近，没有明显的增大或减小的趋势。各年份含水率变程随土壤深度呈不同变化规律，很大程度上是影响土壤含水率分布的各种水文过程相互作用的结果。在降雨最多的2014年，20～40和40～60c m土层中因土壤平均含水率较高，作物根系吸水影响范围较小，土壤水分以垂向运动为主，故变程较小。而在相对干旱的2013年，作物根系吸水的影响范围较大，在作物根系分布密集的土壤剖面，存在较多的水分横向移动，故40～60c m土层含水率的变程较大。

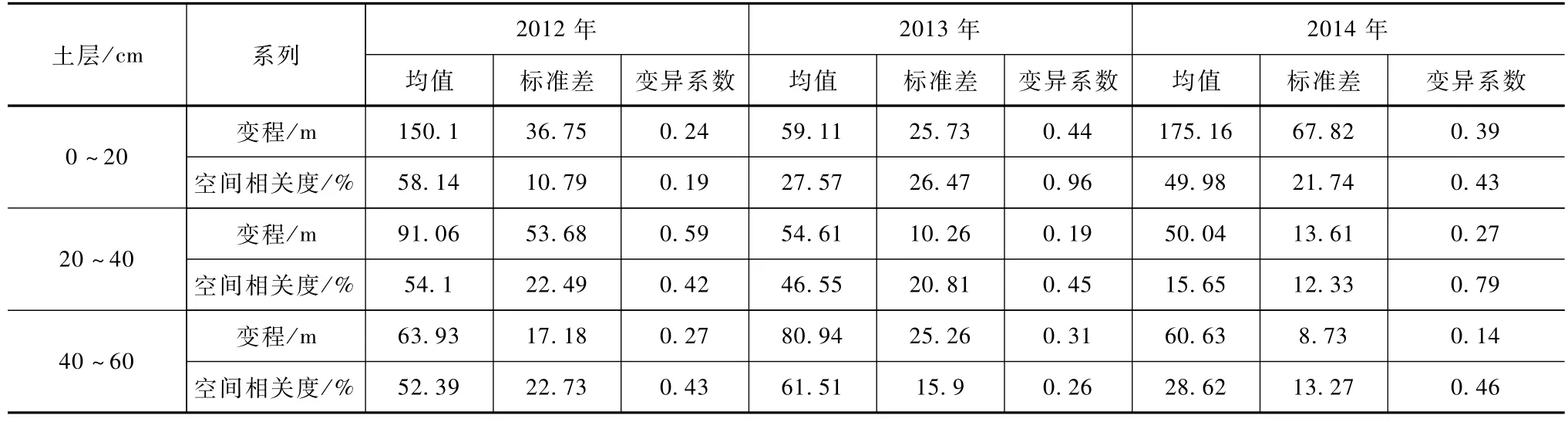
表1 土层含水率变程及空间相关度的统计数据

2.2 剖面土壤含水率空间结构与其均值之间的关系

表2列出了对每年各土层变程、空间相关度分别与土壤平均含水率之间的回归方程。

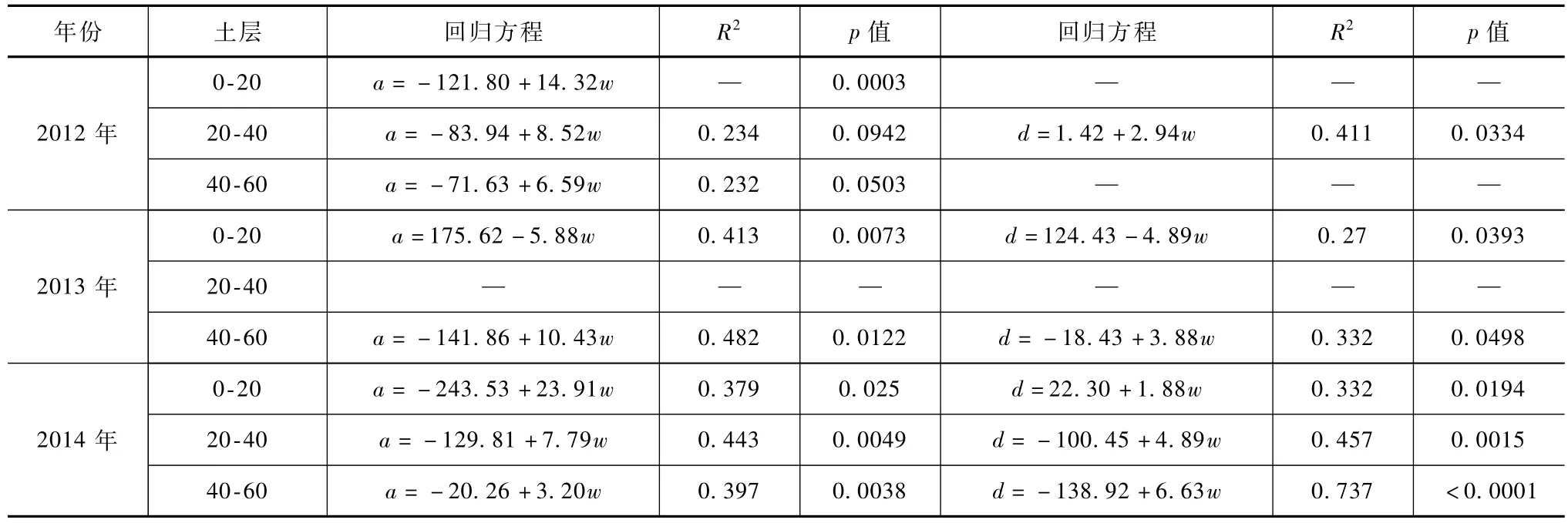
表2 各土层变程(a)及空间相关度(d)与土壤含水率(w)的回归分析

由表2可知，土壤含水率的变程、空间相关度与平均含水率的关系的线性拟合模型在大多数情况下都是显著的，且斜率多为正值，即变程、空间相关度会随平均含水率的增加而增大，这与前述湿润土壤含水率变程大于干燥土壤含水率变程的结论一致。整体来看，2014年变程随含水率增加呈增大趋势，且增速较2012年大。与多数情况下的拟合结果不同的是，在相对湿润的2014年，0～20c m土层的含水率变程随土壤含水率的增加呈增大的趋势，在相对干旱的2013年，0～20c m土层的含水率变程则随含水率的增加而减小。针对2012年0～ 20c m土层含水率变程与平均含水率之间的关系，采用分段线性回归的R2大于简单线性回归的结果证实了这一趋势。另一方面，2013年0～20c m土层含水率的空间相关度随平均含水率的增加而减小的趋势也与其它土层的结果不同。2013年0～20c m土层的含水率变程、空间相关度的不同变化趋势从另一角度说明土壤含水率的时空分布规律很大程度上是由占主导地位的水文过程来决定的。因此，在田间尺度上，土壤含水率空间变异性与其均值的关系会因降雨、灌溉发生时土壤湿润状况及根系吸收等水分运动过程的不同而存在差异，且在表层土壤因影响过程复杂而尤其显著。之前的研究结果也表明不同的降雨、灌溉等因素会通过影响土壤水分运动过程，从而影响土壤含水率空间变异性。

3 结论

本文以棉田实测土壤含水率为基础，结合传统统计学与地统计学的方法，分析了土壤含水率的空间变异特征在土壤不同深度、不同年份的变化规律及其与土壤平均含水率之间的关系。结果表明土壤含水率的空间分布特征在土壤不同深度、生育期内不同时间以及不同年份之间存在差异，而其与土壤平均含水率的关系也随土壤深度、时间的不同而不同。一般来说，降雨较少的年份，较深层土壤含水率的变程大于表层土壤;降雨较多的年份，表层土壤含水率的变程大于深层土壤。与之前的研究结果不同的是，较湿润的年份土壤含水率变程较大，较干旱的年份土壤含水率变程较小。多数情况下，土壤含水率变异函数模型拟合参数随土壤平均含水率的变化可以用线性关系来描述，但斜率在不同深度及不同时间都会有所不同。土壤含水率空间分布特征及其与土壤平均含水率的关系在不同时间存在差异，这很可能是因作物生长差异而导致的根系吸水及土壤水分在水平、垂直方向上运动的空间变异造成的。但在田间试验中，对根系吸水及水分不同方向的运动进行观测具有一定的困难，因此根据现有数据很难定量确定不同因素对土壤含水率空间分布的影响。而采用模型模拟与实测数据相结合的方法，能够较好地控制影响因素，有利于量化不同因素的贡献，应该成为下一步的研究内容。

［1］ManabeS，Delworth T.Thetemporalvariabilityofsoilwetnessanditsimpactin climate［J］.ClimateChange，1990(16) : 185-192.

［2］Huisman JA，SperlC，Bouten W，etal.Soilwatercontentmeasurementsatdifferentscales:accuracyoftimedomain reflectometryandground-penetratingradar［J］.JournalofHydrology，2001，245 ( 1-4) : 48-58.

［3］Vereecken H，Huisman JA，PachepskyY.On thespatio-temporaldynamicsofsoilmoistureatthefield scale［J］.JournalofHydrology，2014(516) : 76-96.

［4］mohantyBP，SkaggsTH.Spatio-temporalevolution and time-stablecharacteristicsofsoilmoisturewithin remotesensingfootprintswithvaryingsoil，slopeand vegetation ［ J］.Advancesin WaterResources，2001，24(9-10) : 1051-1067.

［5］BaroniG，OrtuaniB，FacchiA.Theroleofvegetation and soilpropertiesonthespatio-temporalvariabilityofthesurfacesoilmoistureinamaize-cropped field ［ J］.JournalofHydrology，2013 ( 489 ) :148-159.

［6］杨勇，张若兮.贝叶斯最大熵地统计方法研究与应用进展［J］.土壤，2014(03):402-406.

［7］李金麟，赵琛.地统计方法在黑河上游气象分析中的应用比较［J］.兰州大学学报(自然科学版)，2014(03):318-323.

［8］苏建云.基于综合评分与地统计的晋江市地下水环境质量评价［J］.泉州师范学院学报，2013(06):38-43.

［9］王艺聪，李庚新.基于地统计分析的1974～2004年东北三省夏季气温时空演变规律［J］.安徽农业科学，2013(03): 1223-1225.

S152.7+3

A

1008-1305(2016)05-0052-04

10.3969/j.issn.1008-1305.2016.05.020

2016-03-26

廉 娟(1982年—)，女，工程师。