含蜡原油管道停输再启动可靠性研究

王继平

中国石油大学（北京）油气管道输送安全国家工程实验室（北京102249）

含蜡原油管道停输再启动可靠性研究

王继平

中国石油大学（北京）油气管道输送安全国家工程实验室（北京102249）

传统的确定性方法研究含蜡原油管道停输再启动的安全性存在很多不足，基于可靠性的方法可以很好地解决参数不确定性问题。国内已经有学者开展了停输再启动的可靠性研究。从停输再启动极限状态方程的建立、参数不确定性分析、可靠性分析、目标安全水平确定4个方面，总体评价了含蜡原油管道停输再启动可靠性研究的现状。针对现有研究的不足，提出了今后研究的2个方向：确定更加合理的可接受凝管概率、开发更加高效的算法。介绍了停输再启动失效概率的计算方法，并结合具体算例，指出凝管概率在工程实际中的指导意义：更加合理地确定输油温度和停输时间。

含蜡原油管道；停输再启动；可靠性；极限状态方程；目标安全水平；凝管概率

我国所产原油80%以上为含蜡原油，世界范围内含蜡原油的产量也在不断增加[1]，此类原油输送主要采用加热输送工艺。由于计划停输和事故维修，管道难免遇到停输的情况。管道停输以后，油温与管壁温度的差异导致蜡晶析出，当原油中析出的蜡达到原油质量的2%~3%时，原油整体将发生胶凝[2]。一旦原油发生胶凝，就有可能造成管道停输再启动失败。另外，从经济性的角度考虑，对于长距离加热输送管道，即使很小的降低输油温度也能产生巨大的经济效益。但是输油温度的降低，必然导致安全性的降低[3]。对于热油管道来说，输油温度和停输时间是2个重要的参数。因此，正确评价含蜡原油管道停输再启动的可靠性，合理确定输油温度和停输时间是一项十分必要的工作。

含蜡原油管道停输再启动的安全性与运行参数、油品物性参数、环境参数等诸多因素密切相关，这些参数都具有显著的不确定性[4]。对于参数的不确定性，传统的方法都是确定性方法，比如我国现行管道运行规程规定，对于加热输送管道，要求进站温度高于原油凝点3℃以上[5]。这种做法难以描述参数变化对再启动过程安全性的影响，无法给出科学、准确的评价。针对确定性方法的这些不足，近年来开始有学者引入基于可靠性的设计与评价（Reliability-Based Design and Assessment，简称RBDA）方法研究含蜡原油管道停输再启动问题，通过计算凝管概率来表征停输再启动的可靠性。

RBDA方法是一种概率性方法，以失效概率表征设计和评价对象的安全性。该方法的实施与应用包括以下几个步骤：通过失效模式分析，建立极限状态方程；通过参数不确定性分析，研究极限状态函数中各随机变量的概率分布模型；求解极限状态方程，计算失效概率；安全性评价，即对每种极限状态，将计算的失效概率与最大可接受失效概率比较[6]。笔者将从RBDA方法应用的4个关键步骤论述含蜡原油管道停输再启动可靠性研究的现状，并结合本课题组开发的算法以具体算例展示含蜡原油停输再启动可靠性评价的过程。

1 含蜡原油管道停输再启动可靠性研究现状与展望

1.1 停输再启动极限状态方程的建立

对某一失效模式的极限状态，基于可靠性的设计方法可抽象为载荷S与抗力R之间的关系，对应的极限状态函数见式（1）：

式中：R和S通常是多个随机变量的函数，随机变量的分布函数需要通过不确定性分析确定。

严大凡[7]依据结构可靠性理论，最早提出使用启动压力建立了易凝高黏原油管道停输再启动的极限状态函数，见式（2）：

式中：[P]为管道允许承压能力，MPa，Prestart,min为管道再启动所需最小压力，MPa。

许康[8]在评价管道停输再启动时借鉴使用了该极限状态方程，选择管道最大允许操作压力（MAOP）作为评价基准，并采用Monte-Carlo法对其求解。范华军[9]提出使用MAOP作为评价基准过于保守，推荐使用ISO16708提出的最大允许事故压力（MAIP）作为评价基准，并针对缺陷、无缺陷管道分别推荐了MAIP的取值。若仅以再启动压力是否超压判断管道停输再启动的安全性，显然不够全面。因此，张文轲[10]提出了进站油温低于凝点的极限状态方程，见式（3）：

式中：Tin表示进站温度，℃；Tg表示凝点，℃；n为系数。

管道停输以后，其启动方式依据采用的泵不同可分为恒压启动和恒流量启动两种方式。于鹏飞[11]建立了管道恒压再启动情况下，基于流量恢复的极限状态方程，见式（4）：

式中：Qs为再启动过程中管道末端流量恢复水平，m3/h；Qc为再启动临界安全流量，m3/h。含蜡原油停输再启动的失效模式分析与极限状态方程的建立已基本成熟。

1.2 参数不确定性分析

随机变量的不确定性分析的主要任务是确定安全评价涉及参数的分布模型和分布参数。许康利用Monte-Carlo法对原油黏度、土壤物性、管道埋深和地温4个参数的不确定性进行了模拟，提出“停输再启动安全指数”用来判断停输再启动的安全性，但指数等级的划分缺少依据。范华军[12]总结了不确定性参数常用的分布函数和随机变量分布函数参数的估计方法，并用这些方法对大庆原油屈服应力不确定性分布进行了实例说明。于鹏飞[13]参照西部原油管道[14-15]以及中洛线[16]相关不确定参数的统计结果，统计了与再启动过程相关的不确定性参数的概率分布，从统计结果看这些参数均服从正态分布。目前，可以用来表示不确定性参数的分布函数包括：二项式分布、指数分布、Poisson分布、正态分布、极值分布等，其中正态分布与Poisson分布最为常用。

1.3 可靠性分析

可靠性分析的任务主要是求解极限状态方程。目前，除了本课题组的工作，对于埋地含蜡原油管道凝管概率研究的相关报道较少。马成荣等[17]采用事故树法分析了引起管道发生凝管的各个因素。通过给定各个基事件发生的概率，可求得顶事件“凝管”发生的概率。但是，基事件发生的概率人为给定，缺少依据，存在较大的人为主观性。本课题组针对停输再启动数值模拟开展了大量研究，不断开发、完善计算凝管概率的程序。最早，许康使用Monte-Carlo法求解再启动压力高于MAOP的概率。Monte-Carlo法收敛性差，重复计算结果存在较大不确定性，甚至会导致评价结论相差很大。对凝管这种小概率事件，计算时间长，效率低，无法满足实际要求。因此，范华军在分析了Monte-Carlo法不确定性来源的基础上，提出了组合概率法。该方法可以消除Monte-Carlo法的不确定性，重复计算结果相同，为解决凝管概率计算存在较大不确定性的问题探索了一条途径，但是计算时间仍然无法满足现实要求。张劲军等[18]提出基于特征正交分解（POD）的高效算法，显著地缩短了计算时间和存储空间，使得在常规的台式计算机上进行停输再启动的随机数值模拟成为可能。于鹏飞针对传统的蒙特卡罗抽样效率低、重复性差等特点，引入拉丁超立方抽样用于管道再启动相关不确定性参数的抽样中，与传统的蒙特卡罗抽样方法相比，具有样本覆盖均匀、抽样效率高、收敛性好、精度高和抽样结果重复性好等优点。并提出了采用干涉原理对管道再启动失效概率进行求解的方法，大幅减少了求解小概率事件所需的样本数，并且计算结果重复性好。目前，本课题组开发的计算凝管概率的程序，在普通计算机上运行一次大概需要2天时间，基本能满足实际需求。

1.4 目标安全水平确定

目前，尚没有适用于我国的含蜡原油管道凝管问题的目标安全水平。本课题组针对此问题也开展了大量研究，许康[8]将管道停输再启动安全指数分为5个等级，根据凝管概率是否大于10-5来判断停输再启动安全的可接受性。于鹏飞[13]在参考了相关行业领域内目标安全水平的取值基础上，将10-6作为可接受凝管概率。这2种方法没有考虑不同管道所经地区等级、管道运行参数等不同对再启动安全性的影响，用一个确定的数值作为目标安全水平显然不合理。范华军[12]引入模糊数学理论，采用模糊扩张原理，提出了管道凝管损失严重度与可接受凝管概率之间的对应关系，进而可以根据管道的具体情况，确定出不同管道的可接受凝管概率。虽然该方法在确定可接受凝管概率时考虑了管道的差异性，但在凝管损失严重度等级划分上存在很大的主观性和随意性。

含蜡原油管道停输再启动可靠性研究就是以凝管概率表征停输再启动的可靠性，通过将凝管概率与可接受标准相比较判断再启动是否安全。因此，确定合理的可接受凝管概率、提高凝管概率计算效率是含蜡原油管道可靠性研究的2个关键问题。目前，国内还缺乏统一的凝管问题目标安全水平；本课题开发的算法运行一次仍需要两天时间。因此，这2个关键问题的解决也是停输再启动可靠性研究的方向。

2 停输再启动失效概率计算

目前，失效概率的计算方法有多种，包括一阶二次矩法、雷—菲法、蒙特卡罗抽样法、拉丁超立方抽样等。一阶二次矩法已经证明在计算低效概率问题或高度非线性问题的可靠性时计算精度不高；而蒙特卡罗抽样法计算工作量大，占用机时多。拉丁超立方抽样是一种方差缩减技术，不仅能够减少样本量从而减少计算成本，还可以基于相同的样本量提高计算精度。

含蜡原油管道停输再启动是一个非稳态问题，其热力水力耦合计算数学模型复杂，在分析了这些特点的基础上，引入了拉丁超立方抽样方法来克服传统的蒙特卡罗方法的收敛性差的缺点，大幅减少抽样次数；并采用干涉法对极限状态函数进行求解，得到了一种高效算法求解凝管概率。

2.1 拉丁超立方抽样

拉丁超立方抽样属于分层采样，能够保证采样点覆盖所有的采样区域。与随机采样相比，拉丁超立方抽样极大地降低了达到规定精度所需的采样规模。

本课题组开发的算法中，拉丁超立方抽样算法的具体实施步骤如下[19]：

1）将随机变量X所在概率空间ψ划分为n个区间。对第i个区间，Xi的累计概率可写成：P=(1/n) Nr+(i-1)/n；式中Nr为0到1间的均匀分布随机数。

2）使用变量X的反分布函数F-1得到变量Xi落在该区间上的概率。

3）将变量所在的概率空间ψ划分为n个等概率区间。

4）按照确定的抽样数目对每个概率区间随机抽取N/n个值（N为n个区间总的抽样次数）。

2.2 干涉法求解失效概率

应力-强度干涉模型如图1所示，2个概率密度分布曲线的重叠区域叫作“干涉区”，在此区域内，再启动流量恢复水平有可能低于临界安全流量发生失效。对于凝管问题，g(S)、f(C)分别代表临界安全流量和再启动恢复流量概率密度分布。根据干涉理论，可得失效概率，如式（5）所示，当已知g(S)、f(C)的概率分布时就可积分求得失效概率[20]。但是，对于停输再启动问题g(S)、f(C)的概率分布并不容易获知，或者相当复杂而很难找到其原函数，因此必须依赖于数值解法。

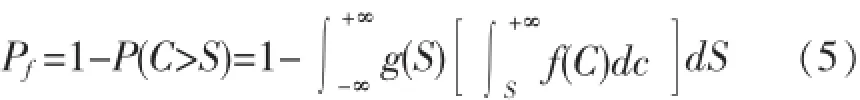
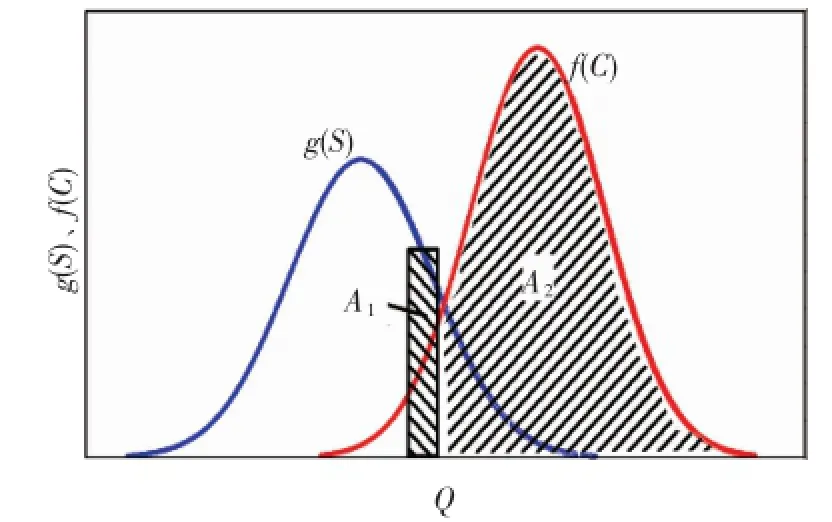
图1 干涉法求解失效概率示意图

对于停输再启动问题干涉法的数值求解算法如下[13]：

1）统计临界安全流量S的概率分布直方图：若样本总数为p，将临界安全输量的最大值和最小值区间等分为m个小区间，记录每个小区间的节点Sj-1、Sj；并统计落在小区间[Sj-1、Sj]内的样本个数，记为gj。

2）同理，统计再启动恢复流量C的概率分布直方图：记其样本总数为q，并将启动恢复流量的最大值和最小值区间等分为m个小区间。

3）将临界安全流量的每个区间，分别和再启动恢复流量的各个区间比较，统计再启动恢复流量小于临界安全流量的样本个数，记为x，则再启动恢复流量小于管道临界安全流量总的概率为也即停输再启动失效概率。

3 算例

以国内某条管道一站间为例，说明采用本课题组所开发的算法对管道停输再启动可靠性评价的过程。该站间管长281km，管道外径为813mm，壁厚为8mm，管输原油凝点均值为3℃，黏温关系见式（6）：

μ=0.018 8T2-1.817 4T+54.286(8℃＜T＜70℃)（6）

具体评价过程如下。

3.1 极限状态方程的建立

管道停输再启动的方式分为恒压再启动和恒流量再启动2种方式。这里考虑采用恒压再启动，以管道末端流量作为评价参数，建立的极限状态方程见式（4）。

3.2 不确定性分析

影响恒压力启动的不确定性参数主要可以分为运行参数、油品物性参数和环境参数3类，见表1。

表1 停输再启动可靠性评价所考虑的不确定性参数

在对现场检测数据统计的基础上，不确定参数的概率分布及取值见表2。

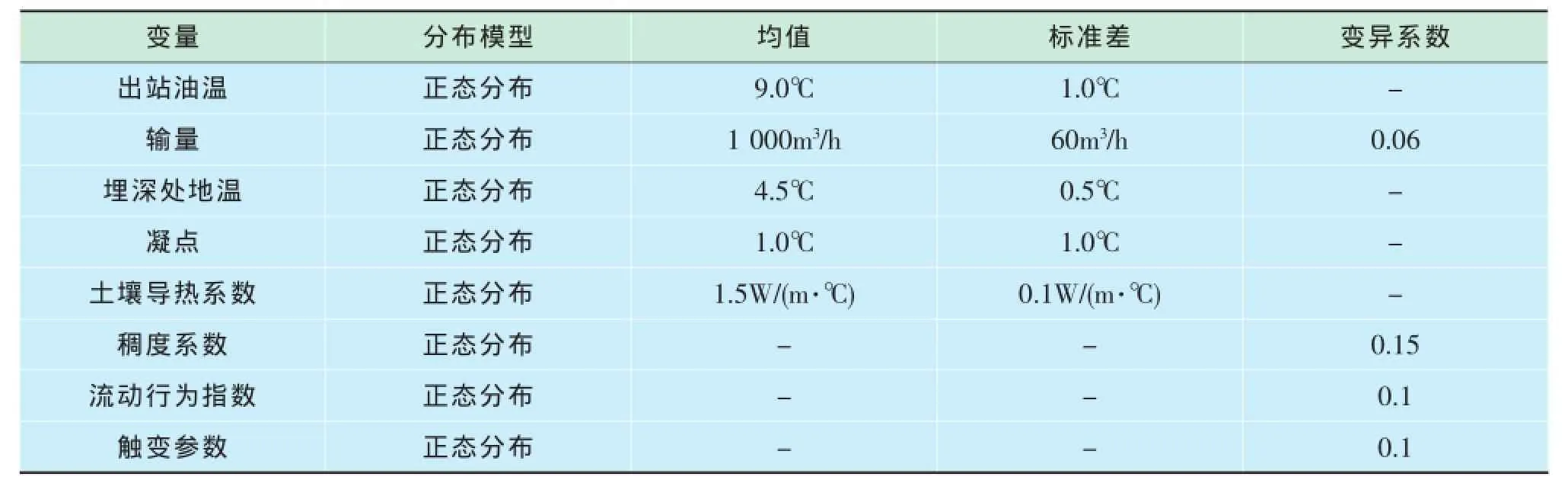
表2 不确定性参数的概率分布选取

3.3 可靠性分析

可靠性分析的方法主要分为数值解法和抽样模拟两类，抽样方法的优点在于直接基于实验结果获得数值解，主要包括模特卡罗模拟、重要性抽样、拉丁超立方抽样。蒙特卡罗法收敛性差，故开发了拉丁超立方抽样的程序，并结合干涉法求解凝管概率[11]。这里，以输量为例（均值为1 000，标准差为60的正态分布），采用拉丁超立方抽样对其进行抽样，结果如图2所示。

图2 流量分布类型

同样对管道末端恢复流量和再启动临界安全流量进行抽样，并依据干涉原理求解极限状态方程，从而得到该条管道停输20h的凝管概率为1.4×10-3。

3.4 目标安全水平确定

在第一部分已经说明，目前还没有确定的统一的适用于凝管问题的目标安全水平，仅推荐使用10-5作为可接受凝管概率。如果，以此作为参考，算例中管段失效概率大于目标安全水平，可以认为其风险比较大，不可接受。有必要采取相应措施，比如：提高进站温度或缩短停输时间。

这里需要指出的是，以上提到算法不仅可以计算特定条件下的凝管概率，还可以通过改变输油温度和停输时间得到不同的计算结果。因此，当已知输油温度和停输时间其中一个时，这些结果可以用来指导另一个参数的确定，对于工程实践具有重要的意义。

4 结论

1）使用确定性的方法评价含蜡原油管道停输再启动问题存在很多缺陷，因此使用可靠性方法重新评价停输再启动的安全性问题十分重要。目前，我国在建立含蜡原油管道停输再启动极限状态方程、影响再启动参数的不确定性分析以及极限状态方程的求解上都取得了重要的成果。

2）计算耗时长、缺少合理的可接受凝管概率是现阶段含蜡原油管道停输再启动可靠性研究面临的主要问题，也是今后研究的两大方向。

3）通过计算凝管概率，当已知输油温度和停输时间两者中某一参数，合理地确定另一参数，有效地改变了过去依据经验确定这2个参数的不足，对于工程实践具有相当重要的意义。

[1]张劲军．易凝高黏原油管输技术及其发展[J]．中国工程科学，2002，4(6)：71-76．

[2]Li H Y，Zhang J J，Yan D F．Correlations between the pour point/gel point and the amount of precipitated wax for waxy crudes[J]．Petroleum Science and Technology，2005（23）：1313-1322．

[3]范华军，张劲军．埋地含蜡原油管道流动安全评价研究[J]．油气储运，2007，26(5)：1-4．

[4]许康，张劲军，尚孟平，等．含蜡原油管停输再启动的安全性问题[J]．油气储运，2004，23(11)：12-15．

[5]油气储运专业标准化技术委员会.原油管道运行规程：SY/T 5536-2004[S]．北京：石油工业出版社，2004.

[6]Petroleum and natural gas industries-pipeline transportation systems-reliability-based limit state methods：ISO 16708-2006[S]．

[7]严大凡，翁永基，董绍华，等．油气长输管道风险评价与完整性管理[M]．北京：化学工业出版社，2005．

[8]许康．埋地含蜡原油管道流动安全性评价方法研究及应用[D]．北京：中国石油大学（北京），2005．

[9]范华军，张劲军，侯磊．原油管道停输再启动安全评价基准研究[J]．石油化工高等学校学报，2007，20（4）：72-75．

[10]张文轲．原油管道停输再启动可靠性分析及随机数值模拟研究[D]．北京：中国石油大学（北京），2011．

[11]于鹏飞，张劲军，宇波，等．含蜡原油管道恒压再启动失效概率研究[J]．工程热物理学报，2014，35（4）：705-709．

[12]范华军．基于可靠性的含蜡原油管道流动安全性评价方法研究[D]．北京：中国石油大学（北京），2008．

[13]于鹏飞．含蜡原油管道凝管概率研究[D]．北京：中国石油大学（北京），2014．

[14]Krewski D,Lemyrea L,Turner M C,et al.Public perception andacceptable levels of health risk among Canadians: health hazards andsources of information[J].Human and E-cological Risk Assessment,2006(12):626-644.

[15]岑慧闲,房淮阳,吴群河.可接受风险的界定方法探讨[J].重庆环境科学,2000,22(3):35-40.

[16]张文轲,张劲军,丁建林.中洛输油管道输量和出站温度概率分布[J].油气储运,2010,29(1):32-35.

[17]马成荣,牛鑫.易凝高粘原油管道凝管失效风险分析[J].油气储运,2007,26(10):1-4.

[18]张劲军，张文轲，宇波．基于POD的埋地热油管道停输再启动模拟高效算法[J]．石油学报，2011,32（1）：167-170．

[19]Xu C G,He H S,Hu Y M,et al.Latin hypercube sampling and geostatistical modeling of spatial uncertainty in a spatially explicit forest landscape model simulation[J].Ecological Modelling,2005,185(2):255-269.

[20]方华灿．油气长输管线的安全可靠性分析[M]．北京：石油工业出版社，2002．

There are many disadvantages in determining the safety of the restarting of waxy crude oil pipeline using the traditional method,but the method based on reliability method can well solve the uncertainty of parameters.Domestic scholars have carried out the research of the restarting reliability of waxy crude oil pipeline.The current situation of the research on the restarting reliability of waxy crude oil pipeline is evaluated from four aspects of the restarting limit state equation establishment,the parametric uncertainty analysis,the reliability analysis and the target safety level determination,and two future research directions to determine the more reasonable acceptable pipeline condensation probability and to develop more efficient algorithm are proposed.This paper introduces the calculation method of restarting failure probability,and points out the guiding significance of the pipeline condensation probability in engineering practice with concrete examples:more reasonably to determine the transportation temperature of oil and the time interval of stopping transportation.

waxy crude oil pipeline;restarting;reliability;limit state equation;target safety level;pipe condensating probability

梅

2015-10-10

王继平（1991-），男，现主要从事原油管道可靠性研究。