基于改进雨林模糊神经网络模型的页岩储层总有机碳含量评价方法

朱林奇，张 冲，魏 旸，郭 聪，周雪晴，陈雨龙

油气资源与勘探技术教育部重点实验室，长江大学地球物理与石油资源学院，武汉430100

基于改进雨林模糊神经网络模型的页岩储层总有机碳含量评价方法

朱林奇，张 冲*，魏 旸，郭 聪，周雪晴，陈雨龙

油气资源与勘探技术教育部重点实验室，长江大学地球物理与石油资源学院，武汉430100

由于采用常规测井曲线评价页岩储层总有机碳含量的精度不高，泛化能力不强，需要大量样本。针对这些问题，改进了神经网络算法，以增加模型的预测能力。利用模糊系统优化细胞神经网络结构，以增强其逻辑推理能力，提高其对模糊数据的敏感性；选择能有效避免“虚拟碰撞”的雨林算法，并针对其存在的缺陷进行改进；利用改进雨林优化算法对网络的初始权值阈值进行优化，避免网络陷入局部极小。分析测井特征曲线的物理意义，选择密度测井曲线与自然伽马能谱测井曲线作为网络的输入，以总有机碳含量作为输出，通过70块岩心样本网络学习与26块岩心样本预测，证明了新网络模型的优越性。结果表明，新模型回判将相对误差从23.189%减小到17.185%，预测相对误差由52.421%减小到15.158%，具有更强的学习能力与泛化能力，更适用于页岩储层总有机质含量的测井评价。

页岩；总有机碳含量；模糊神经网络；改进的雨林算法；泛化能力

1 问题的提出

页岩气藏是典型的“自生自储”油气藏。气体在页岩中主要以游离态气及吸附态气的形式存在，其中游离气存在于天然裂缝及微孔隙中，吸附气吸附于干酪根和粘土表面。由于页岩气特殊的成藏方式，一些反映地层中碳含量高低的参数能大致表征地层中含气量。国内研究表明，总有机碳含量与吸附气、游离气含量均有较好的正相关关系（董大忠等，2012；姜福杰等，2012）。这是因为，随着总有机碳含量的增高，干酪根含量增高，地层吸附气体的也增强，导致吸附气量增大。同时，页岩的生排烃行为在一定程度上形成的多微孔以及微裂缝，改善页岩储层的储集性能，而储集性能的改善有利于游离气含量的增长。总之，总有机碳含量的多少决定了页岩气产量的高低，页岩气要想达到商业开采的标准，必须达到总有机碳含量的最低标准。所以，总有机碳含量计算意义重大，其意义类似于常规油气藏中的含烃饱和度，是非常重要的储层参数。

总有机碳含量（TOC）与页岩产气率有着良好的线性正相关关系，在评价页岩气产气率上有着自己独特的优势（Ross and Bustin,2007;李延钧等,2011）。国内外研究显示，利用元素俘获能谱测井（ECS）、核磁共振测井（CMR）等技术辅助评价总有机碳量的精度较为可靠（Jacobi et al., 2002;Pemper etal.,2010;张晓玲等,2013;赵晨阳等,2002）。但由于测量价格昂贵，在所有井中均进行上述新技术的测量是不现实的，精度较高的测井新技术模型应用性不强。

现阶段常规测井曲线评价总有机碳含量的方法主要有3类：

第1类为ΔlogR法及其改进方法，即利用电阻率与孔隙度曲线叠加预测总有机碳含量（郝建飞等,2012;刘承民,2012;张作清等,2013;钟光海等2015）。存在的问题一是需要首先确定出成熟度的参数LOM，制约了该方法的使用，故现在多用其改进算法；二是logR模型的确定受到人为因素的干扰，因为logR的得到需要先确定细粒的非烃源岩作为基线，基线选择的合适与否决定了logR的预测精度，在刻度确定的情况下，实际情况中有些井难以找到合适的基线，只能选择较为合适的深度段作为基线，精度难以保证。

第2类方法为利用单一特征曲线或者多特征曲线进行拟合计算，如利用自然伽马曲线与TOC建立统计关系，利用干酪根密度较小的概念所提出的补偿密度曲线与TOC单因素拟合的方法，利用补偿密度曲线、补偿中子曲线、声波时差曲线、深电阻率曲线进行多元拟合建模等（Rossand Bustin, 2008;马林,2013;李军等,2014,谢庆明等,2014）。这一类算法的优势是建模方法简单，在精度要求不高的情况下实现较为方便。存在的问题有两个：首先，在建模时由于缺少理论支撑，无法确定测井曲线与总有机碳含量的具体方程而仅能判断具有正相关性或者负相关性，这样的公式精度难以得到保证。其次，在总有机碳含量较小时，由于测井曲线所测得的信息为地层中各类岩石矿物及流体的综合，总有机碳含量的信息必然会被干扰信息所压制，导致其与测井曲线的相关性减弱。

第3类是基于上述问题，近几年提出了神经网络算法预测总有机碳含量的方法，即利用神经网络强逼近函数的能力提升总有机碳含量计算的精度（熊镭等,2014;柳筠,2015;孟召平等,2105）。该方法进一步提升了总有机碳含量计算的精度，使用较为广泛。但传统的神经网络存在着其固有缺点：第一，需要大量样本以便统计其规律，使其具有良好的泛化能力，而因取心昂贵造价高，且实验价格不菲，在实际情况下并不能进行大量的岩心实验；第二，神经网络的权值与阈值初始化时存在着随机性，使得结果容易陷入局部极小，这就使神经网络方法在运用中的可靠性大打折扣。

基于上述分析，笔者尝试对神经网络进行改进，以解决其存在的问题，增加神经网络模型预测可靠性，提升总有机碳含量的测井评价精度。

2 总有机碳含量的测井响应

常规测井系列具有成本低的特点，较非常规测井系列应用更广泛，故本文仅讨论常规测井曲线与总有机碳含量的关系。利用焦石坝地区龙马溪组某页岩气井96块岩心进行相关性分析，发现总有机碳含量与密度测井曲线、自然伽马能谱测井曲线（主要为铀、钾含量以及去铀伽马值）存在着一定的相关性（图1）。

密度测井方法测量地层的体积密度，在总有机碳含量较高时，地层中的干酪根含量较多，而干酪根的密度范围一般为1.1～1.4 g/cm3，故在富含干酪根的地层，密度测井值会存在明显的回落。所以，总有机碳含量应与密度测井值关系密切（图1a）。除了密度测井外，总有机碳含量还与去铀伽马值(KTH)、铀元素(K)、钾元素(U)具有良好的相关性（图1b、c、d），这是因为干酪根中含有放射元素铀，自然伽马能谱测井中测量的铀元素曲线值越高，说明干酪根含量越多，对应的总有机碳含量值应越高。

式(1)为自然伽马能谱测井反推地层铀、钍、钾含量的方程。其中，A1、A2、A3、B1、B2、B3、C1、C2、C3为对应系数，在仪器出厂时就已经刻度完毕，是一个定值。分析该方程组可知，在系数W1、W2、W3变化不大的情况下，若铀含量较高，相应的钍、钾的含量应较低。所以，去铀伽马、钾测井曲线也应与总有机碳含量关系密切，且与铀元素与总有机碳含量的相关性相反。

图1 常规测井曲线响应与总有机碳含量相关关系Fig.1 Correlation between conventional log curvesand totalorganic carbon content

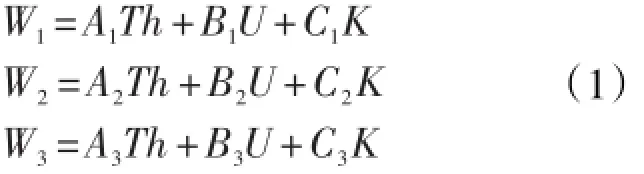
图1显示，虽然上述特征曲线响应与TOC含量之间存在着正相关或者负相关关系，但是这种关系仅能定性的对TOC进行分析，对于定量计算来说精度过低，尤其当TOC含量低时，呈现明显的离散。这是因为常规测井曲线测量的是地层的综合响应，在TOC含量不高时，其所表达的信息必定会被其他信息所压制而难以显现，有必要利用神经网络进行特征数据信息挖掘。

3 雨林模糊神经网络模型及其验证

3.1 模糊神经网络

由于模糊系统与神经网络既有着功能上的共性又存在着相辅相成的理论特点，两者越来越多的被有机的结合在一起使用。模糊神经网络继承了神经网络的强样本学习能力，又由于结合了模糊系统，存在着一定的逻辑推理能力，其方法较旧有的BP神经网络启发性、鲁棒性、透明性均更强，不仅能处理明确的数据，对模糊的数据同样敏感（刘立峰等,2014;徐智浩等,2014）。

模糊神经网络通常由4层组成，分别为输入层、模糊化层、模糊规则层以及去模糊化层，在网络学习时以误差平方和最小为学习目标，利用梯度法与误差反向传播法进行权值的更新。在多层神经网络下，层数越多，其误差反向传播速度越慢（严鸿和管燕平,2009）。这样的后果一是使得网络的学习速度变得异常缓慢，二是容易陷入局部极小值。所以，需要利用优化算法优化权值及阈值，以加快收敛速度，防止局部极小值的产生。

3.2 改进雨林算法

为了克服模糊神经网络存在的上述问题，通常在进行网络训练之前先进行优化算法的寻优，以确定较为合适的权值与阈值，输入到模糊神经网络中进行迭代。笔者选用较新的雨林优化算法，并对其进行改进，以加强其全局寻优能力。

3.2.1 雨林算法（RFA）及其改进思路

雨林算法在2013年被提出（高维尚等，2013；高维尚和邵诚，2014）。考虑到自然界各种动物群体均存在着“碰撞的现象”，而树丛的生长并不存在碰撞，而是有机的向外延伸，吸收阳光，具有模拟动物群体算法所不具备的优势。在算法方面，该算法采用全局分区样与局部分级采样相结合、均匀采样与非均匀采样相结合的思路，以适应未知目标函数的复杂分布，有效避免虚拟碰撞，使算法更易寻找到全局最优解（图1）。

雨林算法虽较其他启发式算法有着明显的优点，但也存在着一些不合理性。比如，其存在着在迭代后期收敛过快的问题，就有可能未能搜寻到全局最优解而可能收敛到局部最优解的凸集。所以，笔者尝试对于雨林算法进行改进，以在最大程度上解决这个问题。考虑到雨林算法的收敛速度主要决定于学习因子α，通过改进学习因子α使其在后期学习中收敛变慢，以较慢的速度、较多的迭代次数去更好的找到全局最优解。

算法行为规划所对应的动态方程组为：

其中，i、j、k、s分别为集合数、迭代次数、决策空间和播种节点的示意次数，n、r、nn为代理的数量、代理的范围和保留播种节点量，α为学习因子。笔者将其改进为一与迭代次数j与最大迭代次数Tmax有关的函数，以达到前期快速确定可行域，后期缓慢在可行域中寻找全局最优解的目的。

3.2.2 改进雨林算法实现步骤

（1）初始树木播种。在优化算法中，需要对初始寻优点进行初始化采样。其采样的合理性决定了算法是否能寻找到全局最优点。在雨林算法中，采样以一种近似均匀的方式进行，来确保有一个以上的采样点进入关键域内，方式类似于树木播种。这种采样方式会使得可行域中留下的最大空白最小。在算法的可行域中以阵列的方式播种，并使得该种子形成根节点进行生长。

（2）萌发。依据信息熵算法计算播种后的信息熵。雨林算法中信息熵计算方法为：

式中，t代表迭代的数目；H为采样的信息熵。

依据信息熵、节点适应度计算采样价值树信息价值与采样价值变化率，以确定下一次迭代中每个播种节点周围新生采样点数量值以及伸展的范围，信息增益越大，伸展的范围越大，采样点数量越多。

（3）生长。依据萌发过程得到的伸展范围以及采样点数，不断更新进行继续采样，并在更新的同时计算信息增益，以确定伸展范围及新生采样点数量。

（4）竞争。进行节点的更新，仅保留若干个较为优势的节点作为下次播种的节点，以增加优势节点的生长能力，使较优节点获得良好的生长的空间。

（5）计寿。若树木在最近的几次生长中适应度增加，则认为为较优树，算法将该雨林节点保存，并跳过播种阶段，直接进行萌发。

（6）繁衍。利用优化结果与实际结果的差异以及迭代次数去衡量程序是否满足了结束的条件。若未满足条件，则继续第一步的播种阶段，在播种时播种更多的树，以便于寻找到全局最优解。

最终，通过雨林算法的优化，可得到较为可靠的神经网络初始权值与阈值。对应的改进雨林算法模糊神经网络流程见图2。

3.2.3 方法验证

利用前人方法建立模型，以便于进行方法与精度的对比。利用BP神经网络模型，以前文所确定的4种特征曲线为输入，以总有机碳含量作为输出，建立4×10××10×10×1的神经网络模型，其中建立1个隐层是因为1隐层结构神经网络即具有逼近一切函数的能力（范佳妮等，2005）。取96块岩心中的70块进行建模，26块进行模型检测。最后得到的神经网络模型学习结果以及预测结果（图3）。

分析图3可以发现，神经网络预测TOC的精度较常规拟合方法精度更高，在精度要求不高的情况下可以达到预测TOC含量的目的。但是，对比学习样本点回归精度与未参与建模样本预测结果，模型预测结果要差于回归结果，这说明神经网络本身固有的泛化能力较弱，对于未知样本点的预测稳定性不高，不确定性强。值得一提的是，由于初始权值与阈值的随机性，神经网络极易陷入局部极小，笔者在建立模型时反复运行了27次，以确定最优神经网络模型。这种带有强人为干扰的模型并不利于TOC含量预测，因为并不了解建立的模型是否为最优模型。

图2 改进雨林模糊神经网络流程Fig.2 The processof im proving the fuzzy neuralnetw ork w ith the im proved rain forestalgorithm

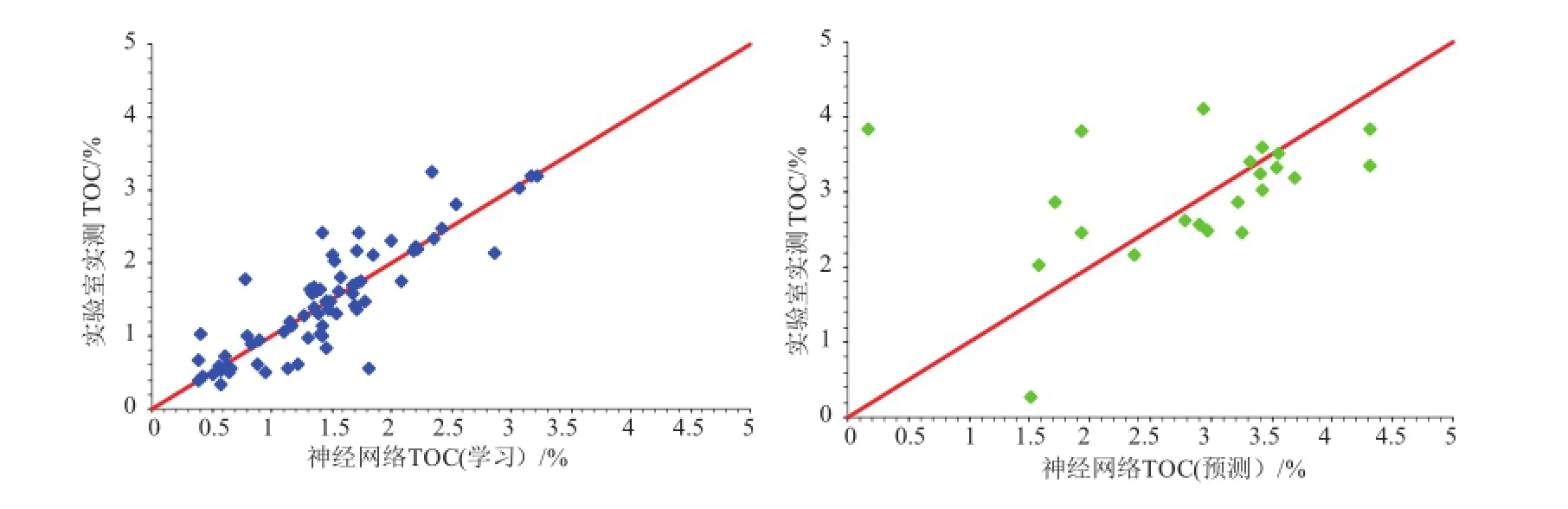
图3 BP神经网络建模精度与预测精度Fig.3 Modeling precision and prediction accuracy of BPneuralnetw ork

利用笔者所提出的改进雨林模糊神经网络进行TOC含量预测。建模样本与预测样本与上述BP神经网络模型建立样本相同，以便于比较两模型在建模精度与泛化能力上的优劣。预测时进行了雨林算法与改进雨林算法的权值阈值优化比较，结果见图4。从优化结果中可以看出，改进的雨林算法（IRFA）虽然在迭代速度上不如原有雨林算法（RFA），但是在寻优能力上强于雨林算法，考虑到改进的雨林算法优化神经网络也仅仅运行了426.32 s，认为笔者提出的改进的雨林算法应更适应于函数的寻优，其寻优效果更明显。

图5为改进雨林模糊神经网络建模精度与预测精度图。对比图3可以看出，笔者提出的方法在建模精度与预测精度上明显优于BP神经网络，尤其是预测精度有较大改善，体现了良好的泛化能力。计算两种模型平均相对误差，运用笔者提出的模型将回归70个样本的相对误差从23.189%降低到17.185%，预测相对误差由52.421%降低到15.158%，建模效果大为改善。这仅仅是运行了1次的结果，并未通过反复运行以确定最优模型。并且，由该相对误差数据可以看出，回归精度反而大于预测精度，说明该模型未存在传统BP神经网络极易存在的过拟合现象，利用笔者提出的方法预测TOC含量时，在样品点达到70个的情况下即可得到较为合理的模型。

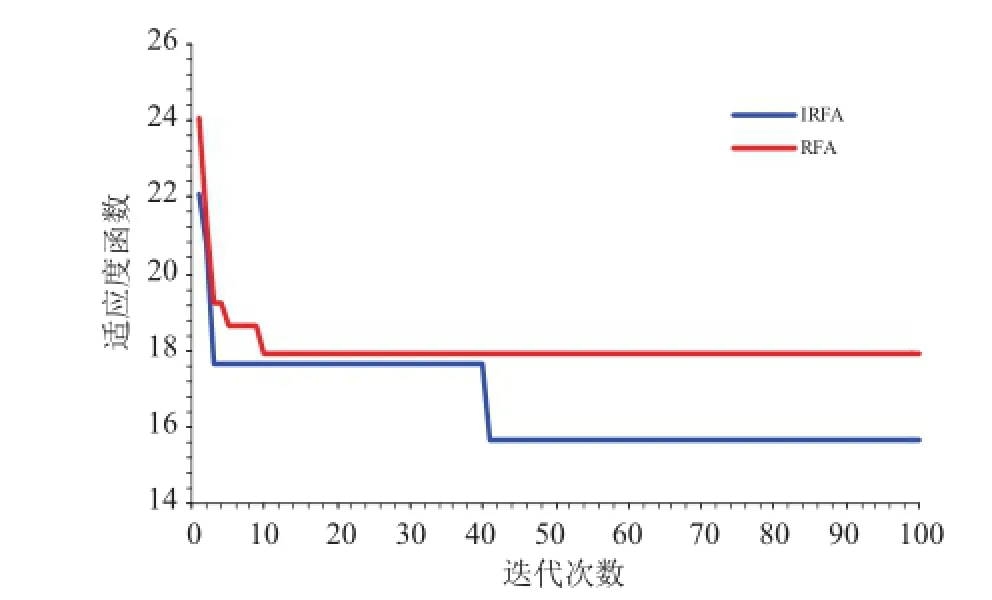
图4 改进雨林算法与雨林算法寻优对比Fig.4 Comparison of the improved rain forestalgorithm and rain forestalgorithm in optim ization

图5 改进雨林模糊神经网络建模精度与预测精度Fig.5 Modeling precision and prediction accuracy of fuzzy neuralnetwork optim ized by the improved rain forestalgorithm

4 实例分析

利用改进模型进行某井段总有机碳含量进行评价，结果见图6。其中，第6道为上述BP神经网络预测模型所评价出来的总有机碳含量曲线，第7道为笔者提出的改进雨林模糊神经网络模型评价得到的总有机碳含量曲线。

对比显示，BP神经网络模型预测曲线总体波动较大，并且在2354～2359m深度段，预测结果在精度和趋势上均严重不符合实际情况。这是因为BP神经网络对输入数据过于敏感，U测井曲线在建模样本点中并不存类似该深度段的较大值。对于这种问题，BP神经网络只有增加样本点的数量以增加精度，若利用该模型将会得到不准确的评价认识。

笔者模型预测曲线波动较小，且预测精度与趋势均较符合实际情况，说明模型具有一定的逻辑思维，尤其在2354～2359m深度段，在建模时未出现类似高铀值样本的情况下，其也能得到较好的结果，体现了良好的泛化能力，优于原始BP神经网络模型预测结果，对总有机碳含量的评价有所帮助。

5 结论

（1）依据岩心与常规测井曲线数据，确定了常规测井曲线与总有机碳含量的相关性及其物理意义，并认为在总有机碳含量较低的情况下，常规测井中所反映的总有机碳含量信息被地层中其他信息所干扰覆盖，使得相关性变差，故需要借助神经网络的数据挖掘能力进行总有机碳含量的求取。

（2）考虑到神经网络固有的问题，借助模糊系统的逻辑推理的能力，应用模糊系统优化神经网络结构，提高其对模糊数据的敏感程度；尝试使用避免“虚拟碰撞”的雨林算法并尝试将其改进，以优化神经网络的初始权值阈值，避免其陷入局部极小。

（3）利用70个样本点对未改进的BP神经网络与改进雨林模糊神经网络分别建模，并利用26个样本点进行预测。结果显示，笔者提出的改进雨林模糊神经网络模型精度较传统的BP神经网络精度更高，并发现建模样本在70个以上时就可得到未过拟合模型。实例分析结果显示，笔者提出的模型更合理，适用于页岩储层总有机质含量的测井评价。

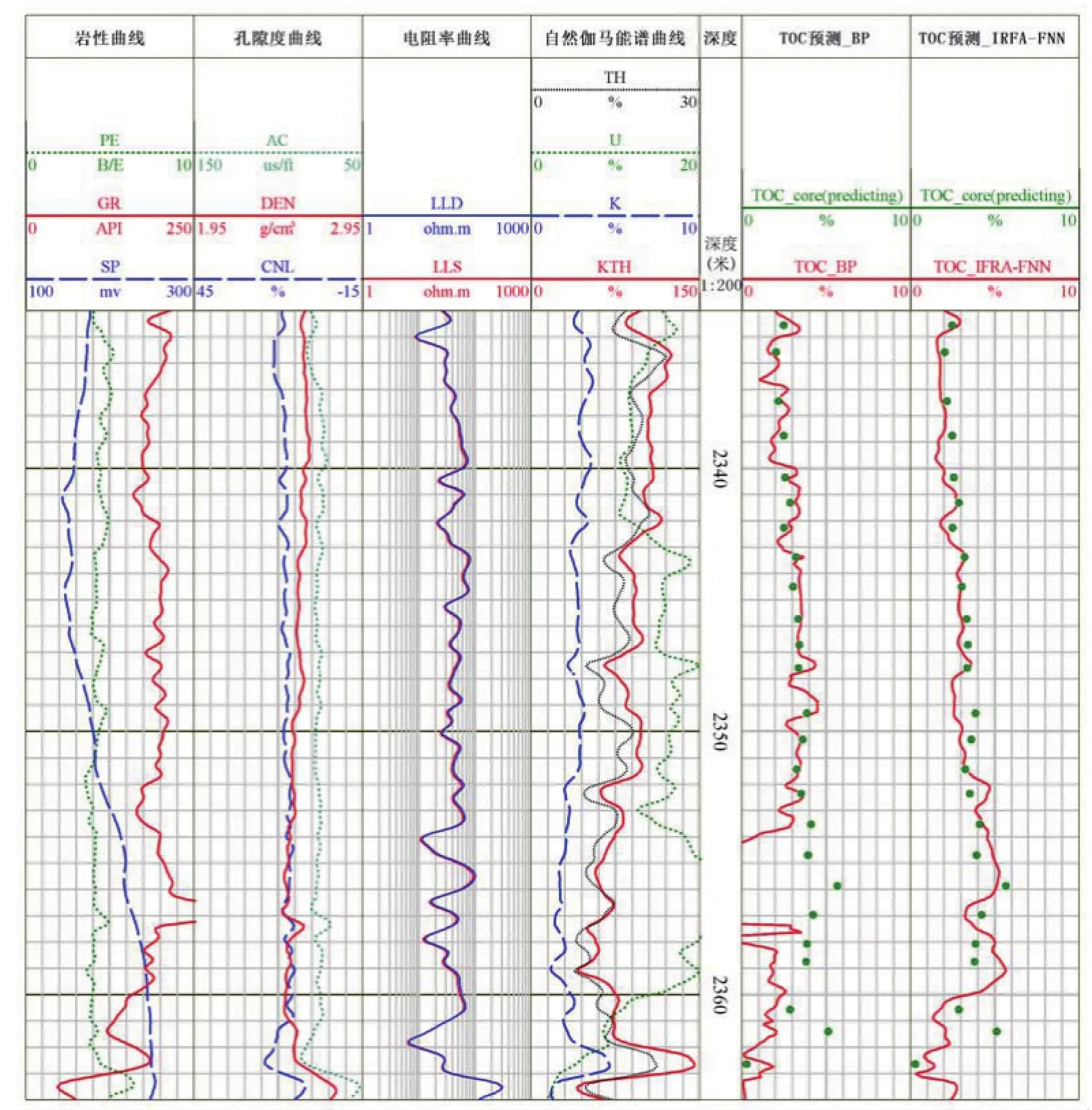
图6 S井某井段总有机碳含量预测对比Fig.6 Comparison of the predicted TOC in a section of Swell

（References）：

董大忠，邹才能，杨桦，等.2012.中国页岩气勘探开发进展与发展前景[J].石油学报，33(S1):107-114.

范佳妮，王振雷，钱锋.2005.BP人工神经网络隐层结构设计的研究进展[J].控制工程，12(S0):105-109.

高维尚，邵诚.2014.复杂非凸约束优化难题与迭代动态多样进化算法[J].自动化学报，40(11):2469-2479.

高维尚，邵诚，高琴.2013.群体智能优化中的虚拟碰撞：雨林算法[J].物理学报，62(19):28-43.

郝建飞，周灿灿，李霞，等.2012.页岩气地球物理测井评价综述[J].地球物理学进展，27(4):1624-1632.

姜福杰，庞雄奇，欧阳学成，等.2012.世界页岩气研究概况及中国页岩气资源潜力分析[J].地学前缘，19(2):198-211.

李军，路箐，李争，等.2014.页岩气储层“四孔隙”模型建立及测井定量表征方法[J].石油与天然气地质，35(2):266-271.

李延钧，刘欢，刘家霞，等.2011.页岩气地质选区及资源潜力评价标准[J].西南石油大学学报（自然科学版），33(2):28-34.

刘承民.2012.页岩气测井评价方法及应用[J].中国煤炭地质，24(8): 77-79.

柳筠.2015.涪陵地区页岩气测井评价参数研究[J].江汉石油科技，25 (3):34-41.

刘立峰，孙赞东，韩剑发，等.2014.量子粒子群神经网络碳酸盐岩流体识别方法研究[J].地球物理学报，57(3):991-1000.

孟召平，郭彦省，刘尉.2015.页岩气储层有机碳含量与测井参数的关系及预测模型[J].煤炭学报，40(2):247-253.

马林.2013.页岩储层关键参数测井评价方法研究[J].油气藏评价与开发，3(6):66-71.

谢庆明，程礼军，刘俊峰，等.2014.渝东南黔江地区龙马溪组页岩气储层测井解释评价研究[J].地球物理学进展，29(3):1312-1318.

熊镭，张超谟，张冲，等.2014.A地区页岩气储层总有机碳含量测井评价方法研究[J].岩性油气藏，26(3):74-83.

徐智浩，李胜，张瑞雷，等.2014.基于LuGre摩擦模型的机械臂模糊神经网络控制[J].控制与决策，29(6):1097-1102.

严鸿，管燕平.2009.BP神经网络隐层单元数的确定方法及实例[J].控制工程，16(S1):100-102.

张晓玲，肖立志，谢然红，等.2013.页岩气藏评价中的岩石物理方法[J].地球物理学进展，28(4):1962-1974.

张作清，郑炀，孙建孟.2013.页岩气评价“六性关系”研究[J].油气井测试，22(1):66-74.

赵晨阳，杜禹，蔡振东，等.2015.国外页岩气储层测井评价技术综述[J].辽宁化工，44(4):473-478.

钟光海，谢冰，周肖.2015.页岩气测井评价方法研究—以四川盆地蜀南地区为例[J].岩性油气藏，27(4):96-102.

Jacobi D,Breig J,LeCompte B,et al.2002.Effective geochemical and geomechanical characterization of shale gas reservoirs from the Wellboreenvironment:Caney and theWoodford Shale[A].SPE124231.

Pemper R，Han X G，Mendez F，et al.2010.The direct measurement of carbon in wells containing oil and natural gas using a pulsed neutron mineralogy Ttool[A].SPE133128.

Ross D JK and Bustin R M.2007.Shale gas potential of the Lower Jurassic Gordondale Member，northeastem British Colunbia，Canada[J].AAPG Bulletin，55(1):51-75.

Ross D JK and Bustin R M.2008.Characterizing the shale gas resource potential of Devonian-Mississippian strata in the Western Canada sedimentary basin:Application ofan integrated formation evaluation[J]. AAPGBulletin，92(1):87-125.

TheM ethod for TOC Content Evaluation in Shale Reservoirs Based on Im p roved Rain Forest Fuzzy NeuralNetwork M odel

ZHU Linqi,ZHANG Chong*,WEIYang,GUO Cong,ZHOU Xueqing,CHEN Yulong
Key Laboratory of Exploration Technologies for Oiland Gas Resources,Ministry of Education,Geophysics and Oil Resource Institute,Yangtze University,Wuhan 430100,China

Theaccuracy ofevaluating totalorganic carbon in shale reservoirs is limited by using conventional logging curvesbecauseof their insufficient generalization ability and requirement of a large number of samples.In view of these problems,neural network algorithm was improved to improve the prediction ability of themodel.The cellular neural network structure was optim ized by using a fuzzy system to enhance its logical reasoning ability and to improve its sensitivity to fuzzy data.The rain forest algorithm,which can effectively avoid the virtual collision,was selected,and its defect of slow convergence in the late learning was overcome.The initial weight value and threshold value of the network were optimized by the improved rain forest optimization algorithm to prevent thenetwork from resulting in localminimum,which can improve theaccuracy and generalization ability of themodel.Based on the analysis of the physicalmeaning of the characteristic curve,the density log curves and the natural gamma ray spectrum logging curves were chosen as the input to the network and the total organic carbon contentwas used as the output.Through the networklearning of 70 core samples and the prediction of 26 core samples,the role of the improved rain forest algorithm and fuzzy logic is proved.The superiority of thenew networkmodel isdemonstrated.The resultshows that the relative regressionalerror of thenewmodel is reduced from 23.189%to 17.185%,and the relative prediction error is reduced from 52.421%to 15.158%,whichmeans that the prediction is in accordance with the real situation of formation.From the above,we learn that the newmodel has better learning ability and generalization ability.Thenewmodel ismore suitable for loggingevaluation of totalorganicmatter content in shale reservoirs.

shalegas；TOC；fuzzy neuralnetwork；improved rainforestalgorithm；generalization

ZHANGChong，Associate Professor；E-mail:yzlogging@163.com

P631.82

A文献标识码：1006-7493（2016）04-0716-08

10.16108/j.issn1006-7493.2016079

2016-05-31；

2016-06-04

国家自然科学基金重点项目（41404084）；湖北省自然科学基金（2013CFB396）联合资助

朱林奇，男，1993年生，硕士，地球探测与信息技术专业;E-mail:445364694@qq.com

*通讯作者：张冲，副教授;E-mail:yzlogging@163.com