基于FEA的钢箱梁吊装施工吊耳有限元分析

张吉庆， 叶智威， 王 媛

(深圳市路桥建设集团有限公司， 广东 深圳 518024)

基于FEA的钢箱梁吊装施工吊耳有限元分析

张吉庆， 叶智威， 王 媛

(深圳市路桥建设集团有限公司， 广东 深圳 518024)

吊耳结构设计直接影响钢箱梁在吊装施工过程中的可靠性和安全性，但是吊耳作为局部受力构件，其受力状态复杂，吊耳板孔在吊轴挤压作用下或吊耳与钢箱梁表面焊接强度不足均易导致吊耳失效。通过对比分析板式吊耳和带加劲板吊耳的受力情况，提出了吊耳结构相的改进措施；通过对比有限元分析与理论公式计算结果，进一步验证了理论公式在计算吊耳孔壁局部挤压应力的适用范围，可为类似工程提供参考依据。

人行桥； 钢箱梁； 吊耳； 有限元； 焊缝

钢结构桥梁施工，需要进行横向分块、纵向分段，预制完成后再运输至现场吊装拼接，各预制构件上设有多个吊耳，吊装完成后将吊耳拆除。吊耳在吊装过程作为局部受力构件，受到复杂的应力作用，因此吊耳的设计会影响整个施工过程，若处理不当则会产生安全事故，因此对吊耳进行强度校核是一项非常重要的任务[1]。

吊耳的强度计算目前并没有特别规范的方法，一般采用理论方法结合经验公式校核，主要包括：吊耳孔与插销挤压强度、吊耳各危险截面强度校核、焊缝强度校核等3个方面，钱亚臣[2]提出了在机械设备上设置吊耳的主要设计原则；万进[3]通过分析耳板式吊耳的受力情况和设计原理，结合实际情况指出在实际工程应用中的不足和失误；韦东辰[4]根据设备本体结构特点、 外形尺寸和受力分析，设计计算出结构合理、利于操作、安全可靠的吊耳。

随着有限元分析技术在吊耳强度分析中广泛运用。刘玉贵[1]借助ABAQUS软件对吊耳结构的接触强度进行研究，对比分析普通板式吊耳和带加强板吊耳的受力情况，依据钢箱梁外形 特点及受力情况，提出了吊耳结构相应的改进措施。肖文勇[5]提出了几种简化处理方法来模拟插销与吊耳的接触。通过有限元计算结果比较，发现提出的简化处理方法与接触算法计算结果接近，且耗时少、操作简单，可以将这些简化处理方法广泛应用于吊耳的有限元强度校核。

本文结合深圳市某人行天桥钢箱梁工程成功设计与安装的实例，说明吊耳的设计和分析方法，并对比分析传统的算法与有限元数值模拟技术两者之间的差别。

1 工程实例

天桥钢箱梁共分为3个预制段，最大跨度24.5 m，全长51.8 m，桥宽处4.3 m，总用钢量102.7 t。钢箱梁截面形式如图1所示。每个块体上分布4个吊耳，吊耳焊接在钢箱梁桥面上，吊点设置具体分布如图2所示。

图1 钢箱梁横截面布置图(单位： cm)

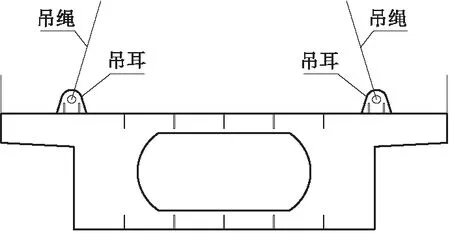
图2 吊点布置横断面示意图

2 钢箱梁吊耳设计

吊耳尺寸选取一般依据钢箱梁外形尺寸、结构特点、受力分布、起吊重量等，本工程所用吊耳采用自行设计、现场焊接施工方法，每个节段用4个板式吊耳，吊耳按横桥向及纵桥向对称布置，纵桥位于节段四分点处，横桥向位置位于箱梁两侧腹板位置，吊耳焊接在主梁顶板上，误差不得超过10 mm，以避免箱梁倾斜，吊装完成后切除吊耳。

钢箱梁在起吊的过程中，吊耳孔处由于受到拉应力的作用，会产生较大的应力集中。在起吊较重的重物时，焊缝的焊接质量无法得到可靠的保证。实际施工时通常会在两侧安装加强板以提高吊耳板的安全系数，这样能达到应力分散的目的，同时提高吊耳的稳定性。

本工程吊装采用临时板式吊耳，吊耳材质为Q235，板厚为28 mm，耳孔附近焊接16 mm的钢板加强。临时板式吊耳与钢箱梁顶板连接采用双面坡口全熔透焊接，板式吊耳大样如图3所示。

图3 吊耳大样图(单位： mm)

2.1 吊耳孔壁挤压应力验算

吊耳强度验算荷载按照最大节段自重荷载计算，每个吊耳受到荷载值N=48.711 kN×10/4=121.78 kN。考虑到起重加速度、主梁晃动及不均匀荷载影响，吊耳安全系数K取1.5。

当吊耳孔壁与吊轴间的间隙较小时，一般使用拉曼公式计算吊耳孔壁的挤压应力，如式(1)所示：

(1)

根据公式(1)计算得到吊耳孔壁挤压应力：

拉曼公式一般仅适用于吊轴与吊耳孔径相差不大的情形，一般要求，Δ=d-d1≤0.02d，但是在实际施工中，为方便吊轴安装与拔出，通常不能满足Δ≤0.02d要求，因此在实际验算中，应当慎重选用该公式计算孔壁挤压应力。本文将在后续内容中讨论此项内容。

2.2 吊耳抗拉强度验算

取1-1截面进行抗拉强度验算，吊耳受到荷载N=121.78 kN，吊耳安全系数K取1.5。

1-1断面扣除空洞后总长度L1=0.124 m，吊耳孔板厚度δ=0.028 m，拉应力：

2.3 吊耳抗剪强度验算

选取2-2截面作为抗剪强度验算截面，吊耳受到荷载N=121.78 kN，吊耳安全系数K取1.5。

2-2截面长度为L2=0.058 m，吊耳孔板厚度δ=0.028 m，拉应力：

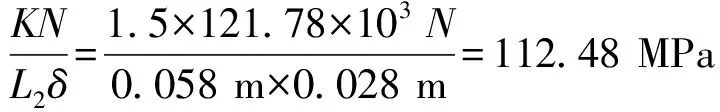
2.4 吊耳焊缝验算

吊耳孔板采用双面坡口焊，焊缝长度Lf=0.29 m，焊缝两端各扣除δ作为有限焊缝长度，吊耳与箱梁顶板要求双面坡口全熔透焊接，角焊缝有效厚度折减系数为0.7，焊缝受到拉应力：

39.8 MPa

3 钢箱梁吊耳有限元分析

3.1 钢箱梁吊耳有限元模型建立

利用专业有限元分析软件MIDAS/FEA进行数值模拟分析，为了对比吊耳在施加加劲板前后的受力差异，分别建立了有加劲板和无加劲板的吊耳模型，为模拟吊耳实际受力情况，增加了焊缝模型及钢箱梁面板模型。钢箱梁每个分段共4个吊耳，材质采用Q235钢。焊缝与吊耳、焊缝与钢箱梁顶板采用刚性连接。

参照文献[5]研究结果，从工程计算角度，可使用径向正弦加载算法替代接触算法以减少非线性分析耗时，因此本文中有限元分析中荷载采用径向正弦加载算法。图4和图5分别为无加劲板吊耳及有加劲板吊耳有限元模型。

图4 无加劲板吊耳模型

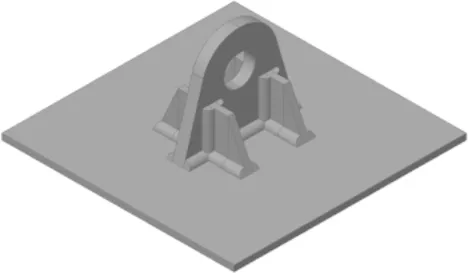
图5 有加劲板吊耳模型

3.2 结果分析

无加劲板情况下，吊耳焊缝Von mises应力值如图6所示，吊耳位移如图7所示；施加加劲板后，焊缝应力分布如图8所示，吊耳位移如图9所示；不施加加劲板的情况下，在焊缝边缘部位出现了部分应力集中现象，无加劲板焊缝应力介于23～114 MPa之间，最大竖向位移0.055 mm；施加加劲板后，焊缝应力介于11～59 MPa之间，最大竖向位移0.002 mm；可见由于采用了加劲板，带加强板的吊耳达到了减小应力增加稳定性的目的。

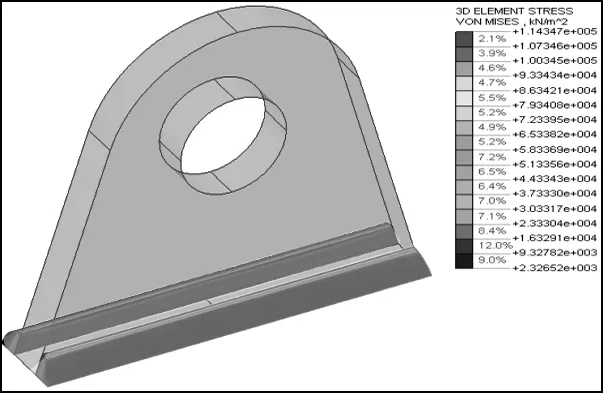
图6 焊缝Von mises应力分布

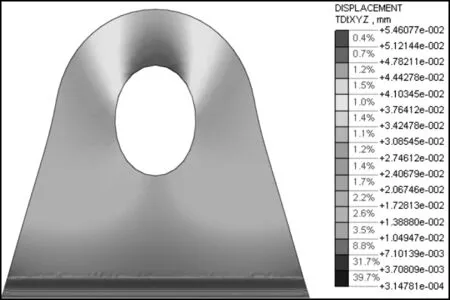
图7 吊耳竖向位移

图8 焊缝Von mises应力分布

图9 吊耳竖向位移

在荷载作用下，吊耳Von mises应力分布如图10所示，在吊耳孔眼处Von mises应力最大值为147.8 MPa，通过拉曼公式计算得到应力值为114.15 MPa，二者相差22%，拉曼公式计算值偏小。

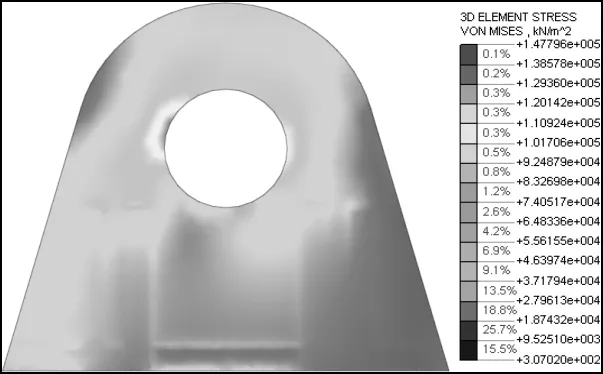
图10 吊耳Von mises应力分布

当吊轴直径d1与吊耳孔眼直径差值Δ=d-d1在(0.02～0.4)d范围内变化时，通过有限元计算结果得到孔壁挤压应力变化范围为：23～147 MPa。通过拉曼公式计算得到孔眼挤压应力变化范围为：114～190 MPa，二者计算结果与Δ值变化趋势如图11所示。根据图11可知，二者计算结果比值如图12所示，根据二者比值可知，当Δ=d-d1≤0.02d时，可以使用拉曼公式计算孔壁挤压应力而不至于产生较大误差，当Δ=d-d1>0.02d时，拉曼公式不再适用，应当采取有限元方法，或者其他有效方法计算吊耳孔壁挤压应力。

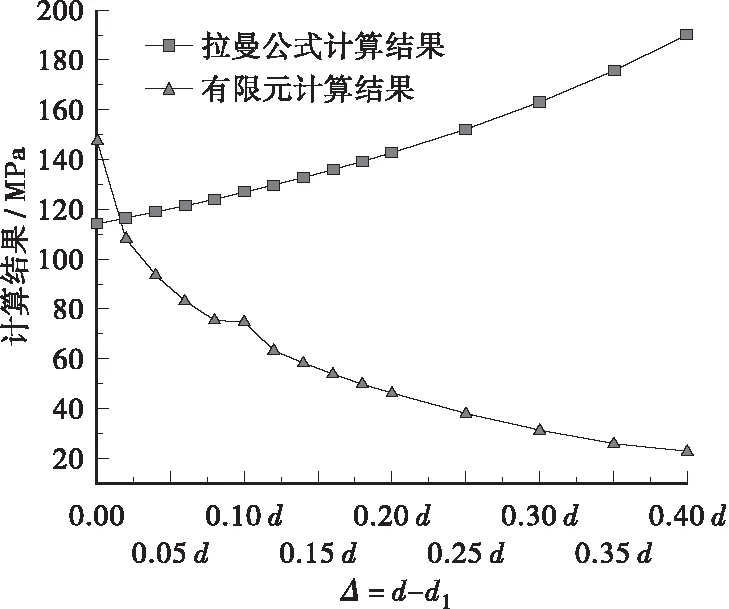
图11 挤压应力计算结果

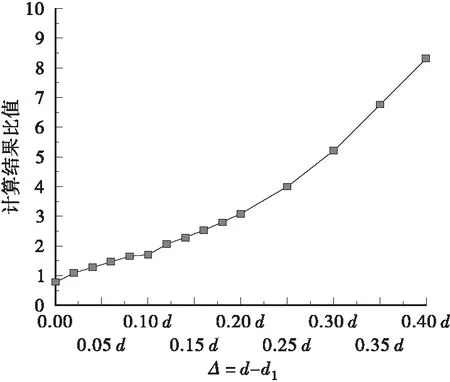
图12 两种计算结果得到挤压应力比值

箱梁结构应力分布如图13所示，在焊缝顶端位置出现部分应力集中，吊装过程中箱梁顶部钢板应力值介于4.7～18.8 MPa之间，应力值较小，因此箱梁顶部钢板始终处于弹性工作状态，受力过程引起的结构变形是可以恢复的，不会产生永久变形，故此结构设计合理，安全可靠。

图13 箱梁顶板应力分布

4 结语

本文对钢箱梁吊耳设计过程及理论公式验算和有限元分析过程进行了介绍，得出以下结论：

1) 吊耳施加加劲板后，焊缝应力范围从23～114 MPa降低至11～59 MPa之间，最大竖向位移减小至0.002 mm；可见由于采用了加劲板，带加强板的吊耳达到了减小应力增加稳定性的目的。

2) 根据有限元计算吊耳孔壁挤压应力与拉曼公式计算结果可知，当Δ=d-d1≤0.02d时，可以使用拉曼公式计算孔壁挤压应力而不至于产生较大误差；当Δ=d-d1>0.02d时，拉曼公式不再适用，应当采取有限元方法，或者其他有效方法计算吊耳孔壁挤压应力。

3) 通过分析钢箱梁顶板应力状态得知，箱梁顶部钢板在吊装过程中始终处于弹性工作状态，受力过程引起的结构变形是可以恢复的，不会产生永久变形，故此吊耳结构设计合理，安全可靠。

[1] 刘玉贵，徐书华，汪雪风，等.基于ABAQUS软件的大吨位钢箱梁施工吊耳的有限元分析[J].钢结构，2015，5(30)：56-59.

[2] 钱亚臣，李毅民.机械设备上吊耳的设计原则[J].起重运输机械，2006(12)：37-38.

[3] 万进，杨刚.军关于耳板式吊耳设计校核的探讨[J].石油化工建设，2010(3)：62-64.

[4] 韦东辰，韦韦.板式吊耳的设计计算[J].小水电，2013(4)：42-44.

[5] 肖文勇，余凯.吊耳局部有限元建模技术分析[J].船舶工程，2009，31(4)：94-97.

1008-844X(2016)04-0125-04

U 448.11

A