焊接速度与T型焊接接头固有应变的相关性

王秋实，张开林，刘 旭

（西南交通大学牵引动力国家重点实验室，四川成都610031）

焊接速度与T型焊接接头固有应变的相关性

王秋实，张开林，刘 旭

（西南交通大学牵引动力国家重点实验室，四川成都610031）

采用热弹塑性有限元方法对T型焊接接头固有应变与焊接速度之间的相关性进行研究。基于有限元软件Sysweld计算得到焊接速度为5～11 mm/s等7个方案下的横向、纵向和等效固有应变值，并绘出焊接速度与横向、纵向和等效固有应变的曲线图，再通过数值分析方法计算其线性相关系数r以验证其线性相关性。结果表明，焊接速度与T型接头横向、纵向及等效固有应变存在良好的线性相关性，且横向固有应变受焊接速度的影响最大，纵向固有应变受焊接速度的影响较小。采用最小二乘法拟合出最佳趋近直线。

焊接速度；固有应变；焊接接头；线性关系

0 前言

焊接作为一种使得构件实现连接的工艺，因其结构强度良好、生产方式灵活等优点，已经广泛应用于各领域。而焊后产生的残余应力和焊接变形极大地影响结构的完整性、经济性和安全性。文献[1]表明，各种影响焊接残余应力和残余变形的因素都可以归根于焊接热输入量和焊件尺寸的作用。而焊接速度既是影响焊接热输入的重要因素，又是工程焊接应用中控制焊接变形的常用手段。因此，研究焊接速度对焊接变形的影响具有一定的工程价值。

T型接头是在各工程领域中应用最广泛的典型接头之一，如高速列车车体及转向架的焊接结构中存在大量的T型接头。固有应变法现已广泛应用于大型工程构件的焊接变形预测中，不可避免的需要对构件中典型T型接头进行热弹塑性有限元分析，以获取准确的固有应变值[2]，因此基于Sysweld焊接仿真软件，采用热弹塑性有限元的方法研究T型接头的固有应变分布规律具有一定的工程意义。

1 焊接变形理论

1.1 Tendon Force概念

按照弹性力学的方法，可以近似的理解为纵向收缩是由于焊缝及其附近区域的纵向收缩力造成的。根据White等人的研究，提出了Tendon Force概念，并通过一系列实验，得出纵向收缩力的计算公式为[3]

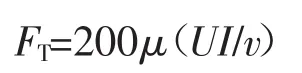
式中FT为纵向收缩力；μ为效率；U为电压；I为电流；v为焊接速度。

1.2 固有变形计算

基于热弹塑性有限元法获取横向固有变形的方法通常是对焊缝及其热影响区的横向残余塑性应变沿焊缝截面进行积分获得。本研究采用一种较为简便的方法来获取T型接头底板的收缩变形。

直线A和B分别为底板板中性面上包含热影响区和焊缝区域的左右边界，如图1所示。通过获得两条直线间距的变化量后即可获得底板横向固有变形S[4]

式中UxA、UxB分别为直线A和B的横向位移。

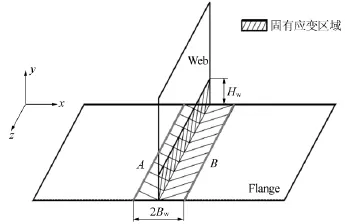
图1 T型接头简图

1.3 固有应变的求解

获得固有变形后，就可以将其转化为相应的固有应变。对于角焊缝，焊接热输入同时施加给底板和腹板。根据科特雷尔能量分配定律[5]，底板和腹板获得的能量计算式为

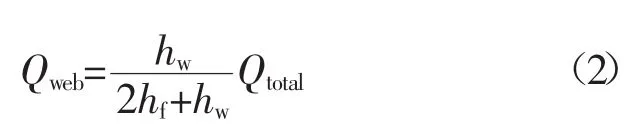
纵向固有应变可以分别由式（3）、（4）计算获得：

若底板的横向收缩为S，则底板的横向固有应变为

由于纵向收缩力对底板的横向收缩有影响，故将其进行修订。通过修正后，纵向收缩力产生的横向固有应变为，故最终的横向固有应变为

式中Qtotal为总的热输入；hw为腹板的厚度；hf为底板的板厚；E为弹性模量；F为总的纵向收缩力；Hw为腹板处产生固有应变区域的高度；Bw为底板处产生固有应变区域的宽度；υ为泊松比。

1.4 焊接热源模型

对于熔化极气体保护焊，采用John[6]提出的双椭球热源模型，其表达式如下

式中Q为有效输入功率；b为熔宽；c为熔深；ff为前半球热流密度分布系数；fr为后半球热流密度分布系数；af为前半球半轴长度；ar为后半球半轴长度。相关参数取值如表1所示。

表1 热源模型参数mm

2 焊接模型的建立

2.1 有限元模型

模型建立过程中未考虑T型焊接接头部分装配因素，如装配间隙等。取试件底板尺寸为120 mm× 96 mm×6 mm，腹板尺寸为120 mm×54 mm×6 mm，焊角尺寸3mm。采用Hypermesh11.0进行网格划分建模。为提高运算效率，又不影响计算精度，焊缝及其焊缝周围等区域细化网格，其余区域粗略表达。单元采用六面体实体单元，单元56474个，节点59143个，如图2所示。建模完成后将模型导入Visual mesh9.0进行计算及分析。

图2 T型接头有限元模型

2.2 焊接工艺及计算方案

T型接头采用CO2气体保护焊，无预热，两焊道方向相同，焊道材料与母材一致，焊接室温20℃；焊接过程中在底板底面三点分别施加xyz、xz、y方向上的约束，冷却过程中释放所有的约束。

焊接工艺参数如表2所示，分别计算焊接速度为5～11 mm/s时的焊后固有应变。

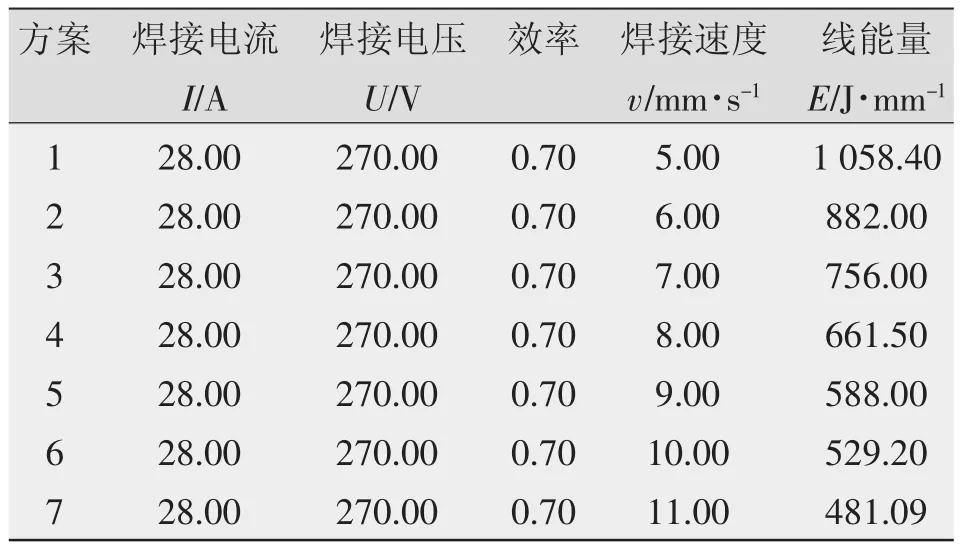
表2 焊接工艺方案参数

3 有限元结果分析

在焊接过程中，固有应变是塑性应变、热应变和相变应变之和。焊接低碳钢等材料不考虑相变对应力变形，冷却后热应变几乎消失，即固有应变近似等于焊后残余的塑性应变。

模型导入Visual mesh 9.0，调用Sysweld的求解器求解上述7个方案，焊接速度6 mm/s时的固有应变图如图3所示，其余方案略。由图3可知，固有应变主要集中在焊缝及其热影响区域，与已有研究结论特征相符[7]。

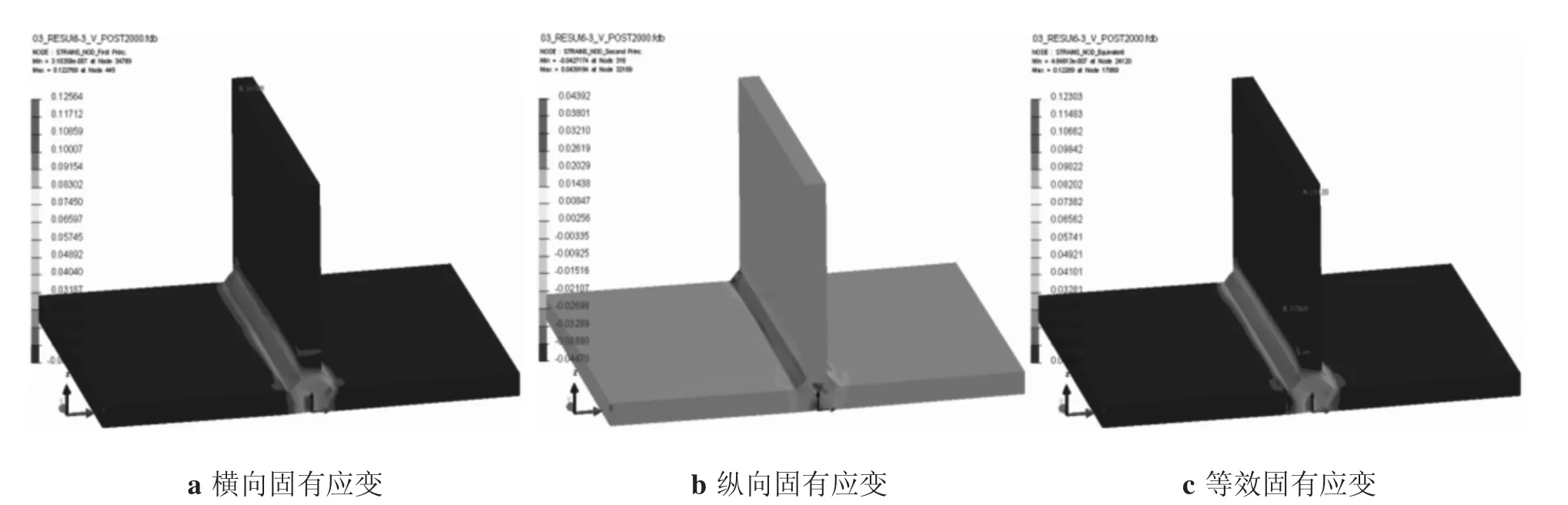
图3 固有应变

3.1 焊接速度与T型接头固有应变的相关性

T型接头在焊接速度为5～11 mm/s下的固有应变计算结果如表3所示。

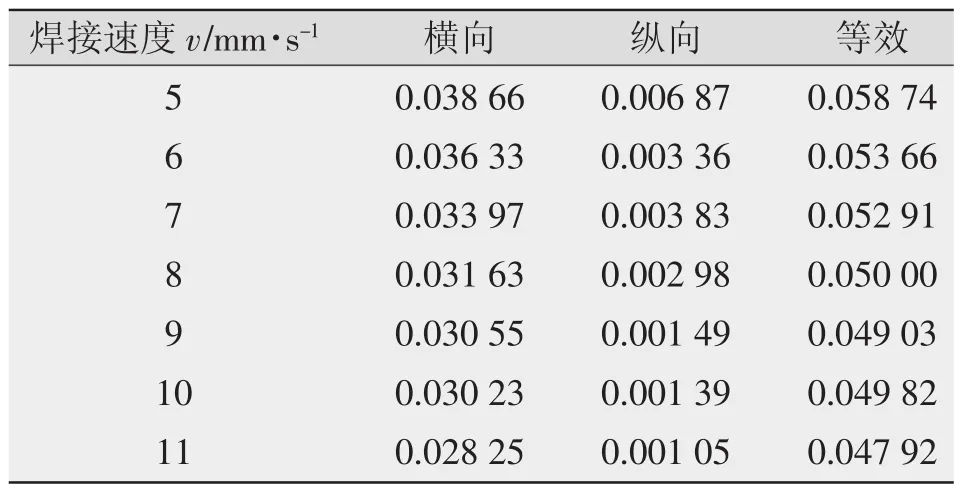
表3 各方案固有应变计算结果

根据表3计算结果，作焊接速度与横向固有应变的曲线，如图4所示；焊接速度与纵向固有应变的曲线如图5所示；焊接速度与等效固有应变的曲线如图6所示。

由曲线图可知，横向、纵向和等效固有应变都随焊接速度的增大而变小，其根本原因是焊接速度的改变影响了线能量。且从曲线趋势来看，横向、纵向及等效固有应变与焊接速度存在类似的线性关系。

图4 焊接速度与横向固有应变曲线

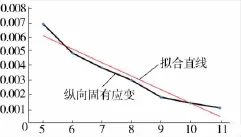
图5 焊接速度与纵向固有应变曲线

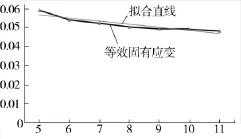
图6 焊接速度与等效固有应变曲线

4 焊接速度与固有应变的线性相关性验证

为进一步说明横向、纵向及等效固有应变与焊接速度中存在的线性相关性，采用数值分析方法检验其线性相关性。

4.1 线性相关系数

数值分析中，检测线性相关性是否良好是通过计算相关系数r来判断。若相关系数r的绝对值越接近于1，则说明两参数的线性关系越好。r计算式如下式，计算结果见图7：

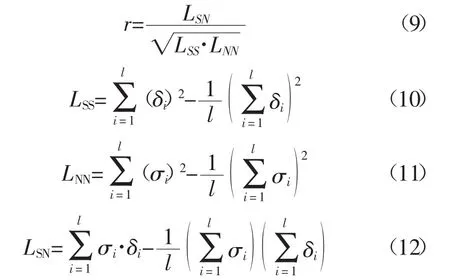
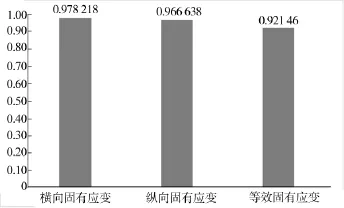
图7 固有应变与焊接速度相关性计算结果

参见表4为线性相关系数的起码值，即若r大于n-2所对应的起码值，则说明截面的应力计算值与过盈量之间的线性关系极为良好。该检验中n=7，线性相关系数的起码值为0.754。由图7可知，所有截面的相关系数远大于0.754且接近于1，说明横向、纵向及等效固有应变与焊接速度之间的线性关系良好。

表4 线性相关系数的起码值

4.2 最小二乘法拟合直线

上述分析结果都验证了横向、纵向及等效固有应变与焊接速度之间有良好的线性关系，由表3的数据结果，用最小二乘法拟合出最佳逼近的直线。拟合计算式如式（13）～式（15）所示

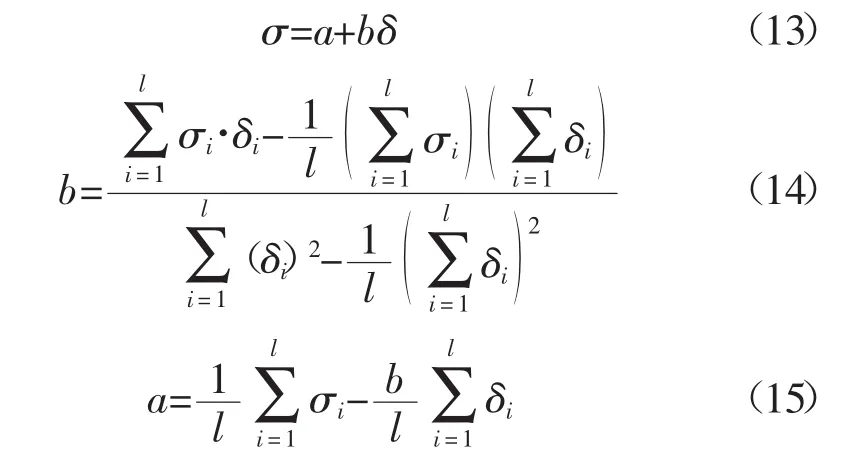
直线拟合参数计算结果见表5，横向固有应变的斜率绝对值最大，即焊接速度对横向收缩影响较大，而对纵向收缩影响不明显。以表5中计算结果作出拟合直线，见图4～图6中的细线，且拟合直线与固有应变曲线变化趋势相近。

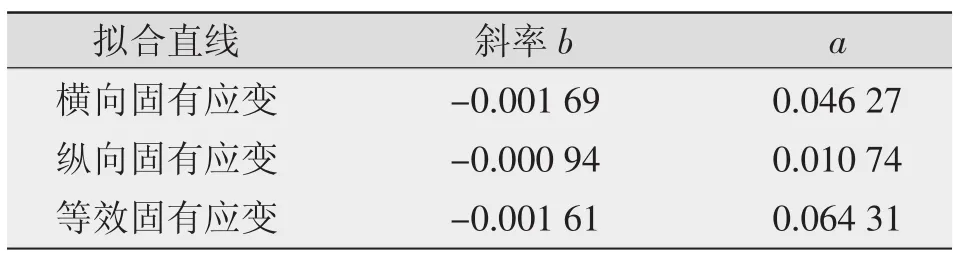
表5 直线拟合参数

5 结论

基于Sysweld焊接仿真软件，采用热弹塑性有限元的方法研究焊接速度对T型接头固有应变的相关性，并通过数值分析方法计算其线性相关性系数r。

（1）T型接头的固有应变主要分布在焊缝及其周围，其中垂直于焊缝方向的横向固有应变较大，沿焊缝方向的纵向固有应变较小。

（2）T型接头的横向、纵向及等效固有应变与焊接速度之间存在较好的线性关系。其中横向、纵向固有应变与焊接速度的线性相关性相比，等效固有应变较好。

（3）T型接头的横向固有应变受焊接速度的影响最大，纵向固有应变受焊接速度的影响较小。

[1]魏武良.固有应变法预测焊接变形的研究及其工程应用[D].上海：上海交通大学，2004.

[2]朱平.基于固有应变法预测转向架焊接变形的研究[D].天津：天津大学，2012.

[3]White J D，Leggatt R H，Dwight J B.Weld Shrinkage Prediction[J].Welding and Metal Fabrication，1980（2）：567-596.

[4]Deng D，Murakawa H，Liang W.Numerical Simulation of Welding Distortion in Large Structures[J].ComputerMethods In Applied Mechanics And Engineering，2007，196（45-48）：4613-4627.

[5]Cottrell C L M.Controlled Thermal Sensitivity Cracking Test Simulates Practical Welded Joints[J].Weld.J，1953（32）：257-272.

[6]John G.A new finite model for welding heat source[J]．Metallurgual Transactions，1984，15B（2）：299-305.

[7]汪建华，陆皓，魏良武.固有应变有限元法预测焊接变形理论及其应用[J].焊接学报，2002，23（6）：36-40.

[8]马思群，袁永文，冯良波，等.焊接速度对铝合金多道焊焊接残余应力影响研究[J].铁道学报，2014，36（1）：16-21.

[9]周宏，蒋志勇，朱枳锋，等.典型焊接接头固有应变的影响因素研究[J].船舶工程，2010，32（5）：53-56.

[10]李庆扬，王能超，易大义.数值分析（第5版）[M].北京：清华大学出版社，2008.

The correlation of welding speed and inherent strain in T-joint

WANG Qiushi，ZHANG Kailin，LIU Xu
（National Key Traction Power Laboratory，Southwest Jiaotong University，Chengdu 610031，China）

Take the thermal elastic-plastic finite element method to study the correlation between welding speed and inherent strain in T-joint.Calculate the transverse，longitudinal，and the equivalent inherent strain values of 7 plans whose welding speed among 5～ 11 mm/s based on the finite element software-Sysweld，and draw up the curve graphs of the welding speed and inherent strain in the transverse，longitudinal and the equivalent.Then calculate the modulus of linear correlation by numerical analysis method to prove the linear relationship of welding speed and inherent strain in T-joint.The results show that there is a good linear correlation between welding speed and inherent strain in T-joint.Finally，use the curve fitting formula to find out the best approaching straight line.

welding speed；inherent strain；welding joint；linear relationship

TG404

A

1001－2303（2016）12－0021-05

10.7512/j.issn.1001-2303.2016.12.05

献

王秋实，张开林，刘旭.焊接速度与T型焊接接头固有应变的相关性[J].电焊机，2016，46（12）：21-25.

2016-04-30

国家自然科学基金（51205324）；牵引动力国家重点实验室自主研究课题（2015TPL-T10）

王秋实（1991—），男，四川泸州人，在读硕士，主要从事机车车辆结构与疲劳强度的研究。