例谈分类讨论“类”之分法
朱海燕●
南京市溧水区第二高级中学(211299)
例谈分类讨论“类”之分法
朱海燕●
南京市溧水区第二高级中学(211299)
在研究和解决数学问题时,当问题所给对象不能进行统一研究,我们就需要根据数学对象的本质属性的相同点和不同点,将对象区分为不同种类,然后逐类进行研究和解决,最后综合各类结果得到整个问题的解决,这一过程就是“分类讨论”.“分类讨论”在高中数学中是一重要的解题策略,具有很强的逻辑性.
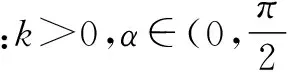
例 已知函数f(x)=ax2-bx+lnx,a,b∈R.
(1)当a=b=1时,求曲线y=f(x)在x=1处的切线方程;
(2)当b=2a+1时,讨论函数f(x)的单调性.
分析 问题(1)参数定值,只要求出切点(1,f(1))及函数在x=1处的切线的斜率k=f′(1),即可给出切线的点斜式方程y-f(1)=f′(1)(x-1).
问题(2)中参数值不知,不同的函数型式具有不同的单调性,需要对函数进行多方面、多层次探究,通常通过导函数的符号研究函数的单调性,是否需要分类待定.
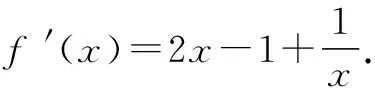

(因为定义域为(0,+∞),所以f′(x)的符号与函数g(x)=(2ax-1)(x-1)的符号保持一致,首先要对g(x)的函数类型进行探究,做一次函数与二次函数的区分,因此需对a是否为0进行初步的分类)
令g(x)=(2ax-1)(x-1).
1)当a=0时,g(x)=-x+1,当x∈(0,1)时,f′(x)>0,f(x)单调递增;当x∈(1,+∞)时,f′(x)<0,f(x)单调递减.
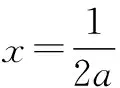
(二次函数在零点求解出的情况下需要对开口方向进行分类,从而在定义域的范围内判断函数值的正负)
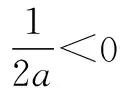
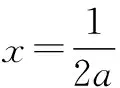
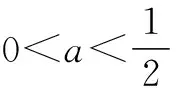
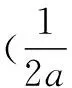
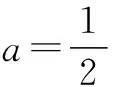
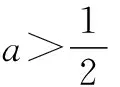
综上所述:(1)当a≤0时,f(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减.
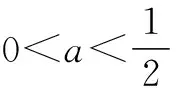
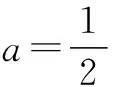
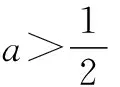
从此函数单调性的讨论可以看到运用分类讨论的思想解题的基本步骤主要由这四步所构成:
(1)确定讨论对象和确定研究的区域;
(2)对所讨论的问题进行合理的分类(分类时需要做到不重复、不遗漏、标准统一、分层不越级);
(3)逐类讨论:即对各类问题详细讨论,逐步解决;
(4)归纳总结,整合得出结论.
G632
B
1008-0333(2016)34-0029-01

