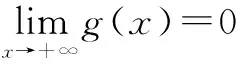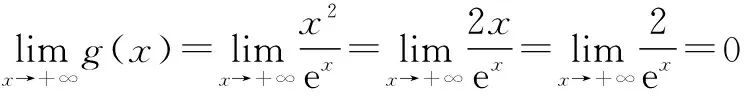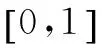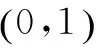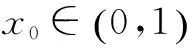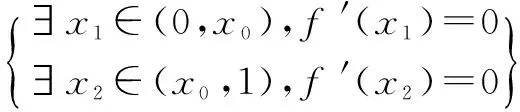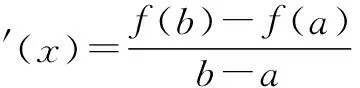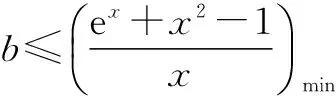导数题中蕴含高数方法
朱小扣●
安徽省无为县牛埠中学(238351)
导数题中蕴含高数方法
朱小扣●
安徽省无为县牛埠中学(238351)
导数题目在高考题中占有重要的份量,而导数题目的解决很多时候会用到高等数学里的函数极限的定义,洛必达法则,罗尔定理,拉格朗日中值定理,琴生不等式等知识.现将平时教学几则案例导数题中蕴含高数方法分析如下.
案例一:与函数极限定义的联系
(2014年福建卷理20题)已知函数f(x)=ex-ax(a为常数)的图象与y轴交与点A,曲线y=f(x)在点A处的切线斜率为-1.
(1)求a的值及函数f(x)的极值;
(2)证明:当x>0时,x2 (3)证明:对任意给定的正数c,总存在x0,使得当x0∈(x0,+∞)时,恒有x2 评析 对于第(3)小问,笔者在教学时,同学们都问我为什么会有两个参数c和x0,为什么关键是找x0.笔者回去仔细琢磨了一下,实际上第(3)小问关键是运用函数极限的定义,就很好理解了.由函数的定义可知: 案例二:与罗尔定理的联系 (2014年四川卷理21题)已知函数f(x)=ex-ax2-bx-1,其中a,b∈R,e=2.71828…为自然对数的底数. 评析 对于第(2)小问,高考命题组给的参考答案很多同学反映看不懂,我觉得参考答案对高中学生而言,确实有一定难度,我觉得这一题如果用罗尔定理,就很简单: 至此,问题得到了简单的转化,很容易就能解决,后面的过程在这里就不再赘述了. 案例三:与拉格朗日中值定理的联系 (1)当m=e时,求f(x)的最小值; 案例四:与洛必达法则的联系 例题 当x>0时,ex≥-x2+bx+1恒成立,求b的取值范围. 解 当x>0时,ex≥-x2+bx+1恒成立. 这种方法使用变量分离和洛必达法则,直接准确地能得到题目的答案,避免了分类讨论的繁琐,与之类似题还有2010年大纲卷理科22题,2011年新课标理21题等. 总结 教师在传授导数的知识时,一定要多想想这题的本源是什么,这一题蕴藏了哪些高数知识,可以和大学中的哪些定理定义有联系.只有教师居高临下,才能观若洞火,才能更好地引导学生去学习,才能达到自身水平的提高.同样学生在学习导数时,如果可以适当地学习一些高数知识,就更可以“一览众山小”,就更可以一招制敌,秒杀诸题! G632 B 1008-0333(2016)34-0004-01