数值模拟在食品冻融过程中的应用进展

岳占凯，万金庆，历建国

(上海海洋大学 食品学院，上海，201306)

数值模拟在食品冻融过程中的应用进展

岳占凯，万金庆*，历建国

(上海海洋大学 食品学院，上海，201306)

文中介绍了有限差分法、有限元法和有限体积法3种应用广泛的离散方式，并对新兴的无网格法在模拟食品冷冻过程时做了简要分析；分析了导热方程与传质方程或电磁方程的耦合这一关键问题，并比较了几种潜热处理方法的优缺点；讨论了人工神经网络法在模拟食品冻融过程时的优势与不足；对近年来热门的微波解冻与射频解冻的数值模拟做了详细论述。

冷冻时间；数值模拟；温度场；人工神经网络；微波；射频；解冻

冷冻食品因其方便、卫生、易保藏等优点，现已成为世界上消费量最大的加工食品，并且处在快速发展阶段。1966年FENNEMA研究发现，冷冻食品的品质取决于冻结速率。食品冻结时,通过最大冰晶生成带的时间越短,冻结品质越好。冷冻设备的能耗主要受冷冻时间和冷冻速率影响[1]。因此,准确计算和预测食品冷冻时间及冷冻过程中的热物性参数,对提高冻品质量、降低生产成本、缩短工艺时间、优化冷冻设备具有重要意义。

食品的冷冻和解冻过程都是发生在一定的温度内的复杂相变过程。密度、比热容、热导率、介电性等热物性参数会随温度发生变化。边界条件、初始条件、食品的形状和成分等都是影响食品冻融过程的关键因素。因此,很难建立精确预测食品冻融过程的通用模型。

数值计算方法将食品热物性参数与冻融过程的流体力学特性相结合，能够准确模拟食品的冷冻和解冻过程。借助计算机，数值模拟方法能够减少实验次数、节约实验经费，而且结果准确可靠，得到了研究者越来越多的关注。本文对近年来数值模拟在食品冷冻和解冻方面的应用进展进行综述。

1 食品的冷冻和解冻过程

冷冻与解冻是2种重要的食品加工工序。冷冻是食品保鲜的关键环节，而解冻同样对食品品质有着至关重要的影响。食品在冷冻和解冻过程中存在着汁液流失、变色、干耗、蛋白质变性、微生物繁殖等问题。为了提高冷冻和解冻食品的品质，更好的设计和优化冻融方法和设备，利用数值模拟方法研究食品冻融过程中的温度变化过程、热量分布情况和冻融时间等问题，受到越来越多研究者的青睐。

2 食品冷冻过程的数值模拟

食品的冷冻过程是一种典型的伴有相变的导热过程，存在一个随时间向热中心位置移动的相变界面，相变界面上的潜热释放使得放热量突增，导致描述食品冻结过程的热物理模型是非线性的非稳态导热方程，数学求解难度很大。数值模拟依据传热学原理,创建数学模型、设定初始和边界条件,然后借助计算机求解。它考虑到了食品在冷冻过程中相变潜热的释放和热物性参数随温度的改变，能有效分析和描述食品的实际冷冻过程。数值模拟法适用于大多数食品冷冻方式,但需要对数学模型及边界条件进行正确的描述。

2.1 建立几何模型

食品几何形状的描述是模拟结果准确性的基础，大体可以分为无限大平板、无限长圆柱体和球体3种基本形状。当食品形状与标准形状差异不大时，可以在原有公式中添加形状因子对食品形状进行近似处理。ILICALI等[2]对原有的形状因子法进行了改进，预测冻融时间，并通过有限圆柱状、球状和椭圆状食品进行实验验证。改进的形状因子法的预测结果与未改进的形状因子法的预测结果相比，绝对平均误差减小了4.0%。在实际运算中，经常遇到跟3种基本形状差别很大的食品，这时需要借助计算机辅助设计(computer aided design，CAD)工具先生成物体形状，然后将其导入网格生成软件进行离散化处理。近些年有研究者利用图像处理技术获取食品实际形状。GOI等[3]提出一种在计算机视觉(computer vision，CV)技术的基础上，利用磁共振成像(magnetic resonance imaging，MRI)技术采集复杂形状食品三维图像的方法。食品不同部位的横截面图像由核磁共振(nuclear magnetic resonance，NMR)扫描获取，横截面图像的边界由B样条曲线插值逼近得到，然后通过得到的光滑横截面边界曲线构造封闭的非均匀有理B样条曲面，再将之转化为三维实体模型。磁共振成像是一种快速高效的非破坏性图像采集方法，特别适用于创建羊、猪、鸡胴体和牛肉半腱肌等结构复杂的食品几何模型。SANTOS等[4]用Matlab等图像处理工具对数码相机拍摄的蘑菇图像依次进行灰度化转换、低通滤波降噪和阈值分割处理，获得高质量的蘑菇二值(黑色背景像素值为0，白色的样品像素值为1)图像，二值图像经过进一步转化，形成蘑菇的二维和三维离散域，然后导入网格生成软件，创建几何模型，模拟其冷冻过程。在创建食品几何模型时，要根据食品的具体形状，合理选择创建方式，以便为后续计算的准确性打好基础。

2.2 设定边界条件

准确设定边界条件，对获取准确的温度场和流场分布至关重要。食品冷冻过程的边界条件主要是指四周表面的换热条件， 常见边界条件有[5]：已知边界温度(第一类边界条件)、绝热边界条件(第二类边界条件)、对流换热(第三类边界条件)、 辐射换热。食品与蒸发板直接接触时，接触面的温度近似为蒸发温度，设置为第一类边界条件；如果食品的温度场对称分布，可以利用对称面只模拟一半，对称面的边界条件设置为绝热；食品以自然对流或强制对流方式进行冷冻属于第三类边界条件；食品的辐射换热需要根据辐射换热量在总换热量中的占比来决定是否考虑。通常情况下，会同时出现几种换热方式，称之为复合热边界条件。在复合热边界条件中，有的换热方式对整个实验结果影响较小，需要根据实验要求的精度来取舍。例如，对于采取强制对流进行冷冻的食品，辐射换热量和自然对流换热量相对很小，可以忽略[6]；对于真空冷冻干燥的食品，水分蒸发(传质)换热是主要换热方式，而辐射换热需要谨慎对待，自然对流换热一般不需要考虑进去[7]。有个别情况，需要同时考虑对流、辐射和水分蒸发。

2.3 控制方程的离散方式

为了得到控制方程较为精确的数值解，需要进行离散化处理，即将几何模型连续的空间求解域划分为有限多个规则或者不规则的网格。通过离散化，得到一组与求解变量有关的微分方程。按照离散原理，常用的离散方式大体可以分为有限差分法(finite difference method，FDM)、有限元法(finite element method，FEM)、有限体积法(finite volume method，FVM)和无网格法(mesh-less method)。

有限差分法是最早采用也是目前最成熟的网格划分方法。将求解域划分为差分网格，用网格节点上函数值的差商代替控制方程中的导数，将网格节点上的值做为未知数创建代数方程。在描述冷冻过程的传热现象时，先写出每个节点的传热微分方程，再利用中心差分法计算每个节点附近的温度梯度。WANG等[8]将有限差分法与Crank-Nicolson式结合，利用二次曲线描述食品热物理性质的变化，建立一维非稳态数学模型预测单体食品冻结时间。预测值与实验值间的线性回归相关系数大于0.989，证明该模型能够比较准确的预测球状、圆柱状、平板状食品在不同温度下的冻结时间和降温过程。章斌等[9]对近平板状食品冷冻过程的3个阶段分别建立全隐式有限差分方程，预测冻结时间，并通过盘装香蕉片和柠檬片进行实验验证。中心温度下降到-20℃时预测值与实验值的最大偏差5.20%,二者吻合较好。SHEEN等[10]为求解食品不同导热过程的数值解建立了显隐式交替的有限差分方程。该方法能有效预测食品冷冻时间，避免了因为食品传热系数高而引起的表面节点温度不稳定问题。也有研究者用该方法研究不规则形状食品的冷冻过程，取得了一定进展。如谢晶等[11]利用有限差分法的焓方程求解鳕鱼在肋板鼓风冻结装置中的冷冻时间，预测结果与实验测量值的偏差小于10%。WIDELL[12]利用二维有限差分法对导热方程进行离散，通过研究鱼在隧道式冷冻装置中的瞬态温度来调节不同冻结阶段的风机转速，在冷冻时间分别增加25%、47%时，风机能耗分别减少19.5%、73.8%。

有限元法把计算域划分为有限个相连但互不重叠的单元，对单元内的节点创建插值函数，借助于变分原理，对微分方程离散求解。有限元法与有限差分法相比，对问题的描述更接近真实情况，计算结果的精度和稳定性也更高。SANZ等[13]针对猪肉冻结过程中生成冰晶的大小和分布问题，利用有限元法对建立的数学模型进行离散，模拟了不同表面冷却速率的产品，能够较好预测肉组织内部不同位置的冻结率。SANTOS等[14]利用Matlab语言编写有限元数值代码，分别建立了整个蘑菇和蘑菇切片的三维不规则食品模型，模拟其冻结时间，并通过实验进行了验证，预测值与实验值的最大绝对误差小于3.2 ℃。HUAN等[15]应用伽辽金有限元法建立模型,研究冷风温度、冷风风速、食品形状等因素对冷冻过程的影响，预测3种基本形状的食品在不同冷冻条件下的冷冻时间。有限元法易于处理复杂边界和高梯度问题，在解决变热物性参数的物理过程方面准确度较高，而且能有效分析形状不规则或者成分不均匀的食品的各类非线性问题。缺点在于物理意义不够明确，在求解运动边界问题时有局限，而且对计算机硬件要求高、求解速度慢。

有限体积法在离散方式上吸收了有限差分法和有限元法的优点，可视为两者的中间产物。利用有限体积法得出的离散方程，在任意控制体内都要求因变量积分守恒，从而在整个计算域内满足守恒原理。这是有限体积法吸引人的优点。MORAGA等[16]用有限差分法和有限体积法分别预测碎肉圆柱体在不同对流边界条件下的温度分布情况，发现有限体积法可更好地模拟冷冻过程，对食品冷冻时间的预测结果也更准确。PHAM[17]利用一维有限体积法预测低含水量、低冰点的一维平板状食品的冷冻时间，将模拟结果与现行的4种冷冻时间计算公式的计算结果进行对比，提出校正因子，将误差控制在10%以内，扩大了计算公式的使用范围，准确度能够满足工程需要。

另外，近年来有研究者用无网格法对食品的冷冻时间进行预测。无网格方法在数值计算中不需要生成网格，而是按照一些任意分布的坐标点构造插值函数，离散控制方程。无网格法避免了网格畸变问题，可以得到比网格法高阶的精确解，而且并不增加计算成本，特别适合模拟各种复杂形状的流场。STEVENS等[18]提出了一种无网格数值方法来预测食品冷冻过程的温度变化，并通过半球状土豆泥进行了验证。首先对导热控制方程的非线性强度进行弱化处理，然后与高分辨率的无网格数值方法相结合，使用三维非结构化数据集得到有效且稳定的数值解。对热导率和比热容进行分段线性拟合，并用8个独立的参数来描述材料的热物性，然后与实验数据进行优化匹配，得到较为准确的温度变化曲线。无网格法能够更加准确的描述与温度具有非线性相关关系的食品的热物理性质，这一特点在模拟食品冻结过程中优势明显。然而，目前国内将无网格法应用到模拟食品冷冻过程的研究鲜有报道。

2.4 潜热处理方法

在食品冷冻过程的导热微分方程：

(1)

式中:ρ，食品密度，kg/m3；C，食品比热，J/(kg·K)；k，食品导热系数，W/(m·K)；T，食品内部各点的温度，K；q，食品内部均匀热源项，W/m3。

对上述偏微分方程进行离散求解，便可以对食品的冻结过程进行模拟。对于大多数食品冻结过程而言，相变并非发生在一个明确的温度值上，而是发生在一个较小的温度范围之内，这样就难以确定一个明确的冻结面。另一难点在于食品的密度、比热容和导热系数等热物性参数在食品冻结前后会发生突变，这将导致描述食品冷冻过程的偏微分方程变得高度非线性，求解难度增大。

为了解决上述2个问题，将食品冷冻过程潜热的释放和热物性参数的变化引入到热传导模型中，而不考虑相变界面在冻结过程中的移动和位置，这种处理方法被称为固定网格法。固定网格法是处理食品冻结问题通用而且有效的方法。根据食品冻结过程潜热项的处理方法不同，固定网格法还可以分为源项法、表观比热容法、焓法和准焓法等方法。

2.4.1 源项法

源项法即将潜热处理成源项，即方程式(1)中的q项[19]：

(2)

2.4.2 表观比热容法

表观比热容法是将食品相变过程释放的潜热与显热叠加，统一表现为比热容的变化，也就是将潜热以显热的形式表示出来，得到一条在冻结点附近有高峰的比热容曲线。然而，潜热的叠加，使得食品的表观比热容成为温度的非连续函数，在一个较小的温差内比热容有一个很大的升降变化，必须对每一步进行内插计算，而且结果较难收敛，导致潜热估计不足。为了提高表观比热容计算的准确度，研究者们提出了很多近似计算方法，但效果都不甚理想[20-22]。另外，可以借助差示扫描量热计(differential scanning calorimetry，DSC)直接测量食品冷冻过程的比热容，此方法在测量少量样品的比热容时较为可靠快捷。DIMA等[23]用数值模型研究螃蟹冷冻过程时，使用DSC测定螃蟹的比热容，作为计算模型的输入量，较好的解决了比热容不准确的问题。

2.4.3 焓法和准焓法

焓法即将潜热的释放合并到焓值的计算中，其基本方程是：

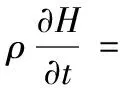
(3)

式中：H，食品的焓值，J/kg；T，食品内部各点的温度，K；ρ、k同式(1)。

准焓法在焓法的基础上通过增加一个比热容估计的步骤和一个温度修正步骤进行潜热处理，避免了大量的迭代计算[24]。在有限差分法、有限元法、有限体积法建立的模型中都有应用。PHAM[25]对几种常见类型的固定网格法在精度、收敛时间、热平衡误差以及计算效果等方面进行了比较，结果显示焓法和准焓法的表现最好。NORTON等[26]建立了基于焓法的一维有限差分模型，模拟圆柱状食品的高压辅助冻结和高压转移冻结过程。该模型对冷冻过程的温度分布、冷冻时间、食品材料的热物理性质以及压力释放时的瞬时结冰量进行了计算，计算结果与相关文献中的实验数据吻合度较高。

近年来，有研究者将焓法与基尔霍夫转换(Kirchhoff transformation)在有限元法中联合使用，对食品冷冻过程进行模拟。基尔霍夫转换是将随温度非线性变化的食品导热系数以积分的形式转化成一个因子，用以优化在不同节点的温度取值问题。这种方法可以减少计算过程的迭代次数，提高计算效率，而且模拟结果与实验结果有很高的吻合度。SANTOS等[27]将有限元法与热焓-基尔霍夫表达式联合使用，对原有导热方程进行转化处理，建立了羊角包和羊肉馅饼的三维冷冻传热模型，预测冷冻过程的温度变化，模拟结果与实验结果的最大绝对误差小于1.3 ℃，准确度较高。

综上，求解冷冻过程的偏微分方程组时，适当的处理可改善建模效果。表观比热容法和准焓法是对食品冷冻过程相变潜热的有效处理，而且准焓法更为精准；基尔霍夫转换的应用提高了模型的运算速度。

2.5 冷冻过程的热质耦合

冷冻过程中食品水分的流失是影响传热过程的主要因素之一。所以，对水分流失较为严重的食品在建立模型时还要考虑传热传质方程的耦合问题。可以用导热方程的焓形式对二者建立耦合表达式：

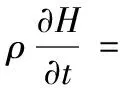
(4)

式中：Hw，扩散物质的焓值，J/kg；mw，扩散物质的质量流量，kg/s。根据菲克定律，质量流量mw=DwW，式中Dw为有效扩散系数，m2/s；W为扩散物质的质量浓度，kg/m3。进而传质控制方程可写为=(DwW)。

上述方程忽略了温度梯度对传质的影响和浓度梯度对传热的影响。对肉类等非孔性食品来说，其内部水分扩散速率十分缓慢，对导热系数的影响小到可以忽略不计，一般只需考虑由于食品表面水蒸气分压力与周围环境水蒸气分压力的差值引起的水分蒸发。PHAM等[28]建立了牛肉冷却过程的热质传递动态模型，利用一维有限差分网格模拟水分在牛肉表面的蒸发过程，二维有限元网格模拟牛肉整体的传热过程，两种模拟同时进行。使用CFD软件来计算局部传热传质系数，分别对计算结果进行拟合，然后将拟合结果应用到模拟牛肉热质传递的有限元模型中，通过实验对照证明牛肉表面的热质耦合模拟结果较为准确可靠。馒头、面包等多孔性食品，主要扩散机理为水蒸气在孔隙间的流动，而且水分转移伴随整个冷冻过程，扩散速率较快。HU等[29]用3步法来模拟圆柱状熟猪肉火腿鼓风冷冻过程的传热传质现象。实验用火腿由碎猪肉制作，作为多孔性食品处理。第1步模拟稳态流场，考虑自然对流和辐射换热的影响。第2步模拟计算对流换热系数，通过刘易斯关系式计算得到对流传质系数。第3步模拟食品传热传质过程，同时考虑对流、辐射换热和水分蒸发。模拟结果显示样品从74.4 ℃降到4 ℃大约530 min，模拟计算干耗为4.07%～4.22%，实验测量干耗约为4.24%，模拟数据与实验数据吻合度较高。在处理不同食品冻结过程的热质耦合问题时，由于孔性食品与非孔性食品内部水分扩散差别很大，要将二者区别对待。

2.6 冷冻过程的热物性参数和传递系数

食品在冷冻过程中水分的相变导致其热物性参数在冻结前后会发生较大变化。食品冻结过程中的热物理性质直接测量难度大、成本高，因此多用数学模型求解。FLOURY等[30]用三维有限元法建立了一个可以在稳态条件下测量复合材料热导率的数值模型。对于离散相热导率与连续相热导率的比值小于1的复合材料，该模型的预测值与实验值的误差范围在3.8%～7.6%，准确度较高。VARGAS等[31]假设食品的热物性参数与温度具有线性相关性，使用有限差分法分析圆柱状食品热物性参数随温度的变化。结果显示，食品的热导率、热容、热扩散系数都对瞬态模型的预测效果产生了明显影响。RINALDI等[32]用Matlab编写了求解傅里叶传热方程的显式有限差分程序，该程序可以在食品杀菌和冻融的温度范围内使用，并且通过采集热渗透曲线进行数据处理来估测食品的热扩散系数。

数值模拟方法在计算食品冷冻过程的对流换热系数中的应用越来越广泛，较为成熟的方法是计算流体力学(computational fluid dynamics，CFD)方法。CFD方法能够有效的计算复杂形状食品的表面局部传热传质系数。HU等[33]分别使用3种紊流模型(STDk-ε模型、LRNk-ε模型、RNGk-ε模型)模拟圆柱状和椭圆状食品鼓风冷却过程中的对流换热和传质系数，并验证了模型的准确性。实验结果表明RNG紊流模型的适用范围更广，预测精度相对较高。VERBOVEN[34]使用数值模拟方法计算了矩形食品冷加工过程中的对流换热系数，在模拟时假定食品表面温度恒定，计算食品表面不同位置的局部对流换热系数，并积分得到了食品的平均对流换热系数。PHAM等[28]利用FLUENT软件，选用RNG紊流模型和加强壁面函数法计算了牛肉胴体在鼓风冷却时不同部位的对流换热系数，并得出拟合公式。

另外，近年来将数值模拟用于预测食品冻结过程中内部水分转移和机械应力变化的研究越来越多。水分及热量在食品不同组织之间的转移和食品冷冻过程的瞬态描述是以后研究的方向和重点。

2.7 人工神经网络法预测冻融时间和热物性参数

近年来,有研究者用人工神经网络法(artificial neural network，ANN)对食品的冻结和解冻过程进行预测。人工神经网络法具有自组织、自适应、自学习特点和强大的输入输出非线性映射能力，使得它在解决非线性问题方面特别有效。人工神经网络法可以对任意形状、成分、大小的食品冻结时间进行预测。MITTAL等[35]开发了一种前反馈神经网络模型，预测简单形状食品的冻结时间。网格的训练数据是用Pham近似模型生成的冻结时间，并且用其它文献中的实验数据进行验证，在150个数据中，有87.4%的数据误差小于10%。GONI等[36]将人工神经网络法与遗传算法结合，建立了一种预测食品冷冻和解冻时间的神经网络模型，该模型适用于任意形状、大小和成分的食品，以文献中报道的各种类型食品的实验数据为依据，得到的平均相对误差小于10%。郭金城[37]在食品冷冻有限差分模型与人工神经网络理论的基础上，设计了以遗传算法为进化算法的径向基函数神经网络模型，对食品冷冻过程进行动态模拟仿真。实验结果表明，该数值模型能够较准确的反映食品冷冻加工过程的规律。钟志友[38]以实际测得的35种果蔬材料的温度、含水率、密度、可溶性固形物含量等参数为输入层，以热导率、比热容、冰点等热物性参数分别单独作为输出层，建立了预测果蔬热物性参数的BP(back propagation)人工神经网络模型。将输出的3种热物性预测参数与实测结果比较，平均相对误差小于3.50%，平均绝对误差小于0.12%,线性相关系数在0.86～0.99，预测结果较为可靠。

对于食品冷冻时间的预测,数值模拟建立的数学模型存在若干假设条件 ,难以准确描述实际的冻结过程。而人工神经网络法就不存在假设条件的问题，可以简单方便、准确快速的预测食品冷冻时间和冷冻过程的热物性参数。人工神经网络法的缺点在于需要大量原始数据对模型进行训练和优化，对研究者的理论知识和计算机编程能力要求较高。目前将人工神经网络法应用于预测食品冷冻时间和热物性参数方面的研究较少，值得国内同行对这一方法的关注和深入研究。

3 食品解冻过程的数值模拟

3.1 传统解冻方法的数值模拟

虽然传统解冻方法(空气解冻法、水解冻法)存在解冻时间长、品质下降较严重、易受微生物污染等缺点，但由于其具有操作简单方便、设备要求低等优点，依然有着广泛的应用。传统解冻方法的数值模拟所用到的控制方程、各项参数、初始及边界条件、潜热处理、离散方式等内容与冷冻过程的数值模拟类似。

纪志坚等[39]建立了圆柱状食品在静水和静止空气条件下的自然解冻数值模型，将有限差分法和元体平衡法相结合，求解食品中心区域、R/2处以及边界节点处的温度和解冻时间。以牛肉为例进行了实验验证，解冻时间的最大误差为8.4%，中心区域、R/2处和边界节点处的温度最大误差分别为1.2、0.8和1.5 ℃，而且数值法得到的温度变化曲线与实验结果有着较高的吻合度。季阿敏[40]针对半球状食品在流动空气条件下的解冻时间及其中心温度变化进行了数值模拟和实验验证。解冻时间的模拟值与实验值最大偏差为6.7%，各个测量点的温度变化曲线基本吻合。KARTHIKEYAN等[41]通过研究美国军用口粮早餐盒中五种不同冷冻食品在常温下的自然空气解冻过程，根据差示扫描量热计测定的五种食物解冻时的热物性参数，建立了一个预测食品常温自然解冻时间和解冻温度范围的有限元数值模型，预测值与实验值的平均偏差在2～5 ℃。将该模型获得的温度变化曲线与微生物或化学动力学相结合，可以用来评价冷冻食品自然解冻后的质量和安全性。

通过求解冷冻食品解冻时间和温度分布，可以在现实中优化改进冷冻食品的物流运输过程。例如根据数值计算得到食品内部温度随时间的变化情况，指导冷藏车制冷机组的启停，在保证冷冻食品正常温度的情况下减少机组工作时间，降低能耗。还可以将数值模拟得到的解冻曲线与解冻过程中的微生物生长曲线相结合，对食品中微生物的腐败行为进行预测，得到冷冻食品暴露在外部温度下的最大安全时间。

3.2 微波解冻和射频解冻的数值模拟

现行的新型解冻方法中，微波解冻和射频解冻由于具有解冻速度快，效率高，汁液流失少，微生物污染小、解冻设备使用寿命长等优点，使得微波和射频解冻技术得到了很快的发展和推广。但同时，它们也存在加热均匀性等问题。通过实验来研究微波和射频的加热过程，优化设备、改善加热均匀性，存在实验周期长、实验成本贵等问题。利用计算机进行数值模拟可为优化微波和射频解冻系统的设计、提高加热均匀性提供重要的信息和一些操作参数。

微波和射频解冻都需要对相变导热过程和电磁场进行复杂的耦合计算。微波解冻时设备内的电磁场能量分布为麦克斯韦波动方程：

(5)

式中：E，电场强度，V/m；μr，相对磁导率；k0，波数；εr，相对介电系数；σ，电导率，S/m；ω0，转盘角频率，rad/s；j2=-1。

射频解冻时电磁波的波长一般要比电极板尺寸和食品尺寸大很多，所以上极板的电势近似固定不变，即假设解冻设备内为准静态电场，根据高斯定理，电磁场的麦克斯韦方程为：

(6)

式中：ε是食品材料的复相对介电常数。

2种解冻方式的食品导热方程与冷冻过程的导热方程一样，但是食品热源项变为：

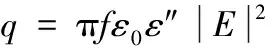
(7)

式中：f为电磁波频率(Hz)；ε0为真空介电常数(8.854×10-12F/m)；ε″为食品材料损耗因子。

LLAVE等[42]通过研究金枪鱼肉在射频辅助解冻过程中热物性和介电性随温度的变化规律，将导热方程与电磁方程耦合，建立了一种射频辅助解冻的三维有限元模型。不加电场时解冻时间为76 min,模拟值与实验值平均相对误差的绝对值为1.2%；射频辅助解冻时间为29 min，模拟值与实验值的平均相对误差的绝对值为3.3%；不加电场解冻后汁液流失率为3.6%，射频辅助解冻后汁液流失率为0.9%。该模型可以预测食品在空气自然对流换热条件下射频解冻过程的瞬态温度分布、样品及周围空气的电磁场强度分布。研究者还利用该模型研究了电极尺寸对温度均匀性的影响。UYAR等[43]利用数值模拟软件建立导热与电磁场的三维耦合模型，对比研究功率放大器射频系统和功率振荡器射频系统在解冻过程中的电场和温度分布情况，并通过不同大小和不同摆放位置的食品进行了实验验证。模拟值与实验值误差都在2 ℃以内。实验还将静止空气解冻与功率振荡器射频解冻的解冻时间做了对比，射频解冻时间是静止空气解冻的1/3。

PITCHAI等[44]建立了一个耦合电磁方程与导热方程的三维微波解冻有限元模型，模拟食品在单频波和不同频谱波段内加热解冻的温度历程。模拟用的频谱波段为符合正态分布的简化频谱波段，频谱波解冻时的电磁功率密度根据不同频率波所占比重加权平均计算得到。研究表明：单频波模型和频谱波模型均能反应出解冻相变过程；单频波的温度模拟值与实验值的平均标准差为13.1 ℃，最大频谱波段温度模拟值与实验值的平均标准差为7.5 ℃，即频谱波段越宽，模拟结果与实验结果吻合度越高；单频波加热解冻的温度均匀性最差，频谱波段越宽，解冻过程的温度均匀性越好。CHEN等[45]建立了一种适用于均质食品的非耦合微波解冻有限元数值模型。一般的微波解冻都是建立电磁方程与导热方程耦合的数学模型，热源项随着每次旋转时食品介电系数的改变而变化，计算量很大，对计算机的要求较高，而且计算时间较长，但是结果较为准确可靠。而非耦合模型中的热源项是定值，该值由在环境温度下食品材料的介电系数计算得到，大大减少了计算量。通过解冻-20 ℃的土豆泥进行实验验证，非耦合模型的6个分散点的瞬态温度的模拟值与实验值的平均标准差为6.6 ℃，耦合模型的平均标准差为6.0 ℃，但是非耦合模型的计算耗时相较耦合模型缩短了93%，说明非耦合模型对温度的影响较小，大大节省了计算时间，更适于工程应用。

微波解冻和射频解冻在缩短解冻时间提高解冻食品质量方面有着光明的应用前景。微波解冻由于波长较短，穿透厚度较小，在解冻体积较大的食品时加热不均匀问题较为严重；射频波长较长，穿透深度大，有助于更好的分配食品和电磁场之间相互作用产生的能量，从而提高加热均匀性。射频解冻的主要缺点在于食品的边角会发生加热过度现象。利用数值模拟方法预测微波和射频解冻过程的电场和温度场不仅可以防止解冻时局部过热，还能为设计和改进解冻装置提供重要依据和关键参数。

4总结与展望

食品的冷冻过程伴随着水分转移、晶核的生成和生长、体积变化、应力变化等现象，这些因素在现有的模型中考虑不够全面，限制了模型的应用范围。现已发表的简化模型大多用于预测单体食品的冷冻时间，对冷冻过程的机械应力变化和内部水分转移的研究较少，而且大都处于研究阶段，用于实际生产过程的更少。现行的商业模拟软件缺少能够准确描述冷冻过程中气体流动(如循环流动、自然或混合流动)的紊流模型，而且对使用者的专业知识要求较高。数值模型使用了一些近似值和理想化的假设，所以模型的可靠性需要实验数据进行验证。

数值模拟技术在食品冷冻和解冻过程的建模、优化和控制方面优势明显。数值模拟能够准确描述食品冷冻和解冻过程的温度变化历程和热量分布情况，对提高食品质量、降低生产成本、提高生产效率、优化设备等具有重要意义。可以预见，数值模拟技术将会成为食品冷冻和解冻领域中强有力的工程工具，而其发展的关键是开发更加实用方便的软件。今后数值模拟技术在食品冻融过程中预测精度的提高，一是要提高测量技术和测量精度，进而减少假定条件，建立更加准确的模型；二是寻找简便高效的模拟方法，选择合适的数值算法，降低计算机运算负荷；三是加强实验数据对模拟计算结果的验证，积累丰富的实验验证资料，为今后模拟技术的进一步发展奠定深厚基础。

[1] CLELAND A C, OZILGEN O. Thermal design calculations for food freezing equipment—past, present and future[J].International Journal of Refrigeration,1998,21(5):359-371.

[2] ILICALI C,TEIK T H,SHIAN L P. Improved Formulations of Shape Factors for the Freezing and Thawing Time Prediction of Foods[J].LWT-Food Science and Technology.1999,32(5):312-315.

[3] GONI S M,PURLIS E,SALVADORI V O.Geometry modelling of food materials from magnetic resonance imaging[J].Journal of Food Engineering,2008,88(4):561-567.

[4] SANTOS M V, LESPINARD A R. Numerical simulation of mushrooms during freezing using the FEM and an enthalpy: Kirchhoff formulation[J]. Heat and Mass Transfer,2011,47(12): 1 671-1 683.

[5] 杨世铭,陶文铨.传热学[M].(第四版).北京:高等教育出版社,2006:44-45.

[6] FERRUA M J, SINGH R P. Modeling the forced-air cooling process of fresh strawberry packages, Part I: Numerical model[J]. International Journal of Refrigeration,2009,32(2):335-348.

[7] COGNEA C, NGUYEN P U, LANOISELLE J L, et al. Modeling heat and mass transfer during vacuum freezing of puree droplet[J]. International Journal of Refrigeration,2013,36(4):1 319-1 326.

[8] WANG Zheng-fu,WU Han,ZHAO Guang-hua,et al.One-dimensional finite-difference modeling on temperature history and freezing time of individual food[J].Journal of Food Engineering, 2007,79(2): 502-520.

[9] 章斌,秦轶,邓其海,等.近平板状食品速冻过程冻结时间的数值计算与实验验证[J].韩山师范学院学报,2014,35(6):78-84.

[10] SHEEN S, HAYAKAWA K. Finite difference analysis for the freezing and thawing of an irregular food with volumetric change[C]∥Spiess W E L，Schubert H．Proceedings of International Congress on Engineering and Food ( Fifth).Engineering and Food: Preservation Processes and Related Techniques Engineering and Food,2:426-441.

[11] 谢晶,厉建国,徐世琼.肋板鼓风冻结装置中食品冻结时间的研究[J].流体机械,2000,29(12):50-53.

[12] WIDELL K N. Energy efficiency of freezing tunnels: towards an optimal operation of compressors and air fans[D].Norwegian University of Science and Technology, 2012:37-38.

[13] SANZA P D, ELYIRAA C, MARTINOB M, et al. Freezing rate simulation as an aid to reducing crystallization damage in foods[J]. Meat Science,1999, 52(3):275-278.

[14] SANTOS M V, LESPINARD A R. Numerical simulation of mushrooms during freezing using the FEM and an enthalpy: Kirchhoff formulation[J]. Heat Mass Transfer ,2011,47(12):1 671-1 683.

[15] HUAN Z J, HE S S, MA Y T. Numerical simulation and analysis for quick-frozen food processing[J].Journal of Food Engineering,2003,60(3):267-273.

[16] MORAGA N O, VEGA G A, LEMUS M R. Numerical simulation of experimental freezing process of ground meat cylinders[J].International Journal of Food Engineering, 2012, 7(6): 11.

[17] PHAM Q T. Freezing time formulas for foods with low moisture content, low freezing point and for cryogenic freezing[J]. Journal of Food Engineering,2014,127:85-92.

[18] STEVENS D, LAROCCA A, POWER H, et al. Estimating the temperature evolution of foodstuffs during freezing with a 3D meshless numerical method[J]. Engineering Analysis with Boundary Elements, 2015,53:46-55.

[19] VOLEER V R,SWAMINATHAN C R.ERAL Source-based method for solidification phase change[J].Numerical Heat Transfer,Part B Fundamentals,1991,19(2): 175-189.

[20] PHAM Q T. Comparison of general-purpose finite-element methods for the Stefan problem[J].Numerical Heat Transfer,1995,27(4):417-435.

[21] CLELAND D J,CLELAND A C,EARLE R L,et al. Prediction of rates of freezing, thawing or cooling in solids or arbitrary shape using the finite element method[J].International Journal of Refrigeration,1984,7(1):6-13.

[22] COMINI G,DEL GIUDICE S,SARO O.Conservative equivalent heat capacity methods for non-linear heat conduction[J]. Numerical Methods in Thermal Problems,1989, 6(Part 1):5-15.

[23] DIMA J B,SANTOS M V,BARON P J,et al. Experimental study and numerical modeling of the freezing process of marine products[J]. Food and Bioproducts Processing,2014,92(1):54-56.

[24] PHAM Q T.A fast unconditionally stable finite-difference scheme for heat conduction with phase change[J].International Journal of Heat and Mass Transfer,1985,28(11):2 079-2 084.

[25] PHAM Q T. Comparison of general-purpose finite-element methods for the Stefan problem[J].Numerical Heat Transfer,1995,27(4):417-435.

[26] NORTON T,DELGADO A,HOGAN E,et al. Simulation of high pressure freezing processes by enthalpy method[J].Journal of Food Engineering ,2009,91(2):260-268.

[27] SANTOS M V,VAMPA V,CALIFANO A, et al. Numerical simulations of chilling and freezing processes applied to bakery products in irregularly 3D geometries[J]. Journal of Food Engineering,2010,100(1):32-42.

[28] PHAM Q T, TRUJILLO F J, MCPHAIL N. Finite element model for beef chilling using CFD-generated heat transfer coefficients[J]. International Journal of Refrigeration, 2009, 32(1): 102-113.

[29] HU Ze-hua,SUN Da-wen. CFD simulation of heat and moisture transfer for predicting cooling rate and weight loss of cooked ham during air-blast chilling process[J]. Journal of Food Engineering, 2000, 46(3): 189-197.

[30] FLOURY J,CARSON J,PHAM Q T. Modelling thermal conductivity in heterogeneous media with the finite element method[J].Food and Bioprocess Technology,2008,1(2):161-170.

[31] VARGAS P,DE RAMOS A L L. Influence of thermal properties accuracy on transient conduction models[C]//14th International Heat Transfer Conference. New York: American Society of Mechanical Engineers,2010, 4:105-113.

[32] RINALDI M,BETTA G, MASSINI R. An innovative mathematical method for the thermal diffusivity estimation and thermal process modeling[C]// 4th International Conference on Simulation and Modelling in the Food and Bio Industry.Ghent: EUROSISS,2006,132-141.

[33] Hu Ze-hua,SUN Da-wen. Predicting local surface heat transfer coefficients by different turbulent k-εmodels to simulate heat and moisture transfer during air-blast chilling[J].International Journal of Refrigeration,2001,24(7):702-717.

[34] VERBOVEN P, NICOLA B M,SCHEERLINCK N,et al.The local surface heat transfer coefficient in thermal food process calculations:A CFD approach[J]. Journal of food engineering,1997,33(1):15-35.

[35] MITTAL G S,ZHANG J. Prediction of freezing time for food products using a neural network[J]. Food Research International,2000,33(7):557-562.

[36] GONIA S M,ODDONE S,SEGURA J A. Prediction of foods freezing and thawing times: Artificial neural networks and genetic algorithm approach[J].Journal of Food Engineering ,2008,84(1):164-178.

[37] 郭金城.食品冷冻加工过程建模与优化[D].吉林:吉林大学,2009:29-42.

[38] 钟志友.果蔬热物性参数与其生理生化指标的内在关系及神经网络预测模型研究[D].上海:上海海洋大学,2010:42-55.

[39] 纪志坚,李徽,于燕,等.圆柱状食品解冻时间的数值求解和实验验证[J]. 家电科技,2015,(12):78-81.

[40] 季阿敏. 半球状食品解冻时间的数值模拟与实验研究[J]. 中国食品学报,2006,6(3):79-83.

[41] KARTHIKEYAN J S,DESAI K M,SALVI D,et el. Effect of temperature abuse on frozen army rations. Part 1:Developing a heat transfer numerical model based on thermo-physical properties of food[J]. Food Research International,2015,76(3): 595-604.

[42] LLAVE Y,LIU S X, FUKUOKA M, et el. Computer simulation of radiofrequency defrosting of frozen foods[J].Journal of Food Engineering,2015,152:32-42.

[43] UYAR R,BEDANE T F,ERDOGDU F, et el. Radio-frequency thawing of food products-A computational study[J]. Journal of Food Engineering,2015,146: 163-171

[44] PITCHAI K,CHEN J J,BIRLA S, et el. Modeling microwave heating of frozen mashed potato in a domestic oven incorporating electromagnetic frequency spectrum[J]. Journal of Food Engineering 2016,173: 124-131.

[45] CHEN J J,PITCHAI K,JONES D, et el. Effect of decoupling electromagnetics from heat transfer analysis on prediction accuracy and computation time in modeling microwave heating of frozen and fresh mashed potato[J]. Journal of Food Engineering,2015,144:45-57.

Progression of numerical simulation in the research of food freezing and thawing process

YUE Zhan-kai, WAN Jin-qing*, LI Jian-guo

(College of Food Science & Technology, Shanghai Ocean University, Shanghai 201306, China)

With the development of computer performance, the application of numerical simulation has gained more and more attention in the study of food freezing and thawing process．Accurate calculation and prediction of food freezing and thawing process are important to shorten the processing time, improve the quality of frozen products, optimize refrigeration systems and save energy consumption. Application of artificial neural network in the research of food freezing process is discussed. Finally, the simulation of microwave and radio-frequency thawing of food products was introduced.

freezing time; numerical simulation; temperature field; artificial neural network; microwave thawing; radio-frequency thawing

10.13995/j.cnki.11-1802/ts.201612041

硕士研究生(万金庆教授为通讯作者,E-mail: jqwan@shou.edu.cn)。

863计划(2012AA092301)资助项目

2016-04-24，改回日期：2016-05-18