定积分元素法应用条件辨析
潘红艳,骆冰翘
(1湖北理工学院 数理学院,湖北 黄石 435003;2华中师范大学第一附属中学,湖北 武汉 430223)
定积分元素法应用条件辨析
潘红艳1,骆冰翘2
(1湖北理工学院 数理学院,湖北 黄石 435003;2华中师范大学第一附属中学,湖北 武汉 430223)
定积分在计算不规则图形的面积、体积及线长时具有重要作用,其中元素法充分体现了定积分的思想,是一种能很好的解决某些量计算的重要方法,确定积分元素是其关键.积分元素依据满足元素法应用条件的有效近似方法而确定,文中结合实例,针对元素法的应用条件,探讨了函数在直角坐标,参数形式及极坐标下的有效近似方法.
定积分;元素法;积分元素;有效近似
0 引言
定积分的应用是积分学中的重要内容之一,而元素法是应用定积分解决某些量的计算的重要方法,确定积分元素是其核心和精华.在传统的教科书中,往往侧重于应用元素法建立一些几何、物理量的计算公式,其实更重要的是,如何应用元素法将一个量表达成为定积分.在此过程中,必须慎重辨析元素法的应用条件.
1 元素法
用定积分解决实际问题的计算,严格来说,要经过“分割”、“近似”、“求和”、“求极限”4个步骤,但这一过程过于繁琐,依据定积分“化曲为直,以直代曲”的思想,可以将这一过程规范简化成如下步骤[1]:
1)选取一个变量如x为积分变量,并确定相应的变化区间[a,b].
2)任取小区间[x,x+dx]⊂[a,b],求出这个小区间对应部分量△U的近似值,若△U≈f(x)dx,则有积分元素dU=f(x)dx.
以上过程即称为元素法.这一方法的应用必须严格遵循如下条件:
1)所求量U是与变量x的变化区间[a,b]有关的量.
2)U对于区间[a,b]具有可加性.
3)部分量△U的近似值dU=f(x)dx与△U之差必须是关于△x(即dx)的高阶无穷小.
其中,dU=f(x)dx称为量U的积分元素,元素法应用的关键在于找到积分元素dU.虽然计算部分量△U的近似值的方法常常有很多,但忽视了条件(3)即△U-dU=o(△x),就会导致错误的结果.
2 有效近似
满足条件(3)的部分量△U的近似计算方法,我们称之为有效近似,其表达式即是要求的积分元素dU.
命题1 由连续曲线y=f(x)(x≥0),与直线x=a,x=b及x轴围成的曲边梯形面积的积分元素为dA=f(x)dx.
有效近似验证[2-3]:
取x为积分变量,则x∈[a,b],在任一小区间[x,x+△x]⊂[a,b](△x=dx)上的部分面积近似于矩形,即△A≈f(x)dx=dA.
因为f(x)连续,则在[x,x+△x]上有最大值M和最小值m,因此,m△x≤△A≤M△x,于是:

由于f(x)具有连续性,当△x→0时,m-f(x)→0,M-f(x)→0,则有:

类似可以验证广义曲边梯形面积积分元素dA=[f(x)-g(x)]dx的有效性.

有效近似验证:
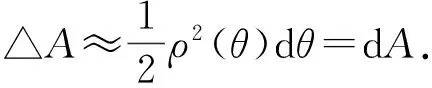






另一种求法:



验证如下:
依据命题1已经验证的曲边梯形面积积分元素的有效近似方法[4],计算[t,t+△t]上的部分量△A(由对称性,仅考虑第一象限内面积):

于是:
≠0.
即△A-dA≠o(△t),条件(3)不满足.
3 结束语
元素法的应用条件(3)是否满足,是正确应用元素法的关键,在实际应用中,逐一验证近似的有效性太过繁琐[5-6],因此,通常是依据几种常见的有效近似方法进行验证,如直角坐标系下的平面图形面积的有效近似,极坐标系下的平面图形面积的有效近似,旋转体体积的有效近似,曲线弧长的有效近似,曲面面积的有效近似等,再结合实际问题推广应用.
[1] 同济大学数学教研室.高等数学[M]. 6版.北京:高等教育出版社,2007:272-274.
[2] 陈玉,贺秋林.微元法原理探究[J].大学数学,2001,17(3):95-96.
[3] 张新建,朱健民.关于“高等数学”教材对定积分元素法处理的几点注记[J].大学数学,2008,24(2):163-166.
[4] 徐月.定积分元素法的应用[J].高师理科学刊,2015(7):29.
[5] 赵翠新.充分利用元素法进行二重积分计算的教学[J].赤峰学院学报(自然版),2015,31(19):23-24.
[6] 史书慧.运输问题最小元素法的一个原则[J].沈阳工程学院学报(自然科学版),2015,11(3):286-288.
(责任编辑 高 嵩)
Discrimination about Application Conditions of Infinitesimal Method to Definite Integral
PanHongyan1,LuoBingqiao2
(1School of Mathematics & Physics,Hubei Polytechnic University,Huangshi Hubei 435003;2No.1 Middle School Attached to CCNU,Wuhan Hubei 430223)
Definite Integral plays an important part in computation of the area,volume and long line of irregular solid.Infinitesimal method fully demonstrates the concept of definite integral and it is an important method to calculate some certain amount.The key point is to determine the integral elements.Integral element is on the basis of the effective approximation method that could meet the application conditions of infinitesimal method to determine.Based on some examples,this paper explores approximate method of functions under rectangular coordinate,parameter equation and parlor coordinate in accordance with the the application conditions of infinitesimal method.
definite integral;infinitesimal method;integral element;effective approximation
2016-11-24
潘红艳,讲师,硕士。
10.3969/j.issn.2095-4565.2016.06.010
O172.2
A
2095-4565(2016)06-0045-03
——辨析“凌乱、混乱、胡乱、忙乱”

