商业楼宇型微网的应急能量管理策略

崔仪，刘念，陈奇芳

(新能源电力系统国家重点实验室(华北电力大学)，北京市102206)

商业楼宇型微网的应急能量管理策略

崔仪，刘念，陈奇芳

(新能源电力系统国家重点实验室(华北电力大学)，北京市102206)

在配电网停电后，商业楼宇型微网进入孤岛运行状态。为减小停电给用户带来的损失、维持停电期间内对重要负荷的供电，针对光储型商业楼宇微网，提出了考虑计划停电与非计划停电2种情况的应急能量管理策略。在计划停电时，以减小停电损失、维持供电时间为目标建立了优化模型，并引入权重因子以权衡二者的重要程度；为减小预测误差对结果的影响，提出了滚动优化策略。在非计划停电时，以优先考虑对重要负荷供电为原则，制定了实时应急方案。通过算例对比分析可知，该策略可有效调节可控负荷投入量，从而实现预期目标。同时，在算例中进行了灵敏度分析，不同的权重因子可灵活调节减小停电损失与维持供电时间在优化目标中的比重。

计划/非计划停电；应急能量管理；滚动优化策略；商业楼宇型微网；微网

0 引 言

微网(microgrid，MG)作为解决电力系统众多问题的一种重要辅助手段，已引起各国科学家的广泛关注[1-4]。MG是未来智能配电网实现自愈、用户侧互动及需求响应、分布式电源接入电网的有效途径[5]，极大地改善了用户与配电系统的供电可靠性，增强了抵御自然灾害与应对突发故障的能力[6]。配电网故障时，MG可以与非故障停电区域内的部分负荷组成供电孤岛，帮助其尽快恢复供电。同时，MG可以向配电网输送功率，有利于更多用户实现网络恢复重构[7-9]。

目前，对传统配电网供电恢复策略的研究较多，其主要思路是在确保系统安全运行的条件下，通过网络重构，快速恢复对非故障区域失电负荷的供电[10]。随着对MG研究的逐渐深入，将MG作为研宄对象，分析其在配电网故障、非计划孤岛切换后供电恢复中的作用，也已取得一系列的研究成果。文献[11]提出在MG非计划孤岛切换后，通过分布式电源动态自组，逐步向周边失电节点恢复供电，最终形成稳定的MG孤岛运行。文献[12]提出了一种混合编程技术来求解直流MG重构问题，从而恢复MG供电、减小停电损失。为在大电网停电后恢复对辐射状配电系统中重要负荷的供电，文献[13]提出了一种MG组建计划。文献[14]提出了一种利用自治MG来降低线路负荷水平的故障恢复方法，通过增加供电恢复成功率来提高系统的运行可靠性。柴油发电机组具有可靠、稳定、灵活、敏捷等特性，可作为MG的应急备用。尤其在太阳能与储能发电量不足时，可作为MG的主电源供电[15-16]。然而，现有的研究成果主要针对包含柴油发电机组、光伏(photovoltaic，PV)、储能系统(energy storage system，ESS)等微源的MG，对一些缺少柴油发电机组的商业楼宇型MG(commercial building microgrid，CBMG)却鲜有涉及。

本文针对配电网停电情况下含有光储系统而不含柴油发电机组的CBMG，提出一种考虑计划停电与非计划停电2种情况的应急能量管理(emergency energy management，EEM)策略。主要包括包括：(1)在计划停电时，考虑PV与负荷的波动性，以减小停电损失、维持供电时间为目标建立优化模型，提出滚动优化策略以减少PV预测误差对结果的影响；引入权重因子以权衡减小损失与维持供电二者的重要程度；在算例中进行对比分析与灵敏度分析；(2)在非计划停电时，以优先考虑对重要负荷供电为原则，制定实时应急方案，该方案可根据每个时刻PV预测值的大小，动态决策可控负荷投入量；在算例中进行对比分析。

1 CBMG结构及组成

CBMG主要由PV、ESS、电动汽车(electric vehicle，EV)、AC/DC双向变流器、负荷、MG中央控制器(micro-grid central controller，MGCC)以及底层控制器等构成[17]。ESS可以平滑PV波动，也可以作为应急电源。AC/DC双向变流器可以实现直流电源与交流电源之间的双向功率转换[18]。CBMG中的负荷可分为2种：可控负荷与重要负荷。EV的充电倍率可调，空调、冰箱等温控类设备的温度也具有一定的可调性，次要照明设备可根据CBMG的需求及时断开，在配电网停电后，均可作为可控负荷接受CBMG的统一调节，但调节幅度直接影响用户的满意度。CBMG以必要照明设备、控制模块及部分计算机设备等作为重要负荷，要尽可能地维持其供电时间。底层控制器分为3种：负荷控制器(load controller，LC)、微源控制器(micro-source controller，MC)与EV控制器(EV controller，VC)。CBMG的结构及组成如图1所示。

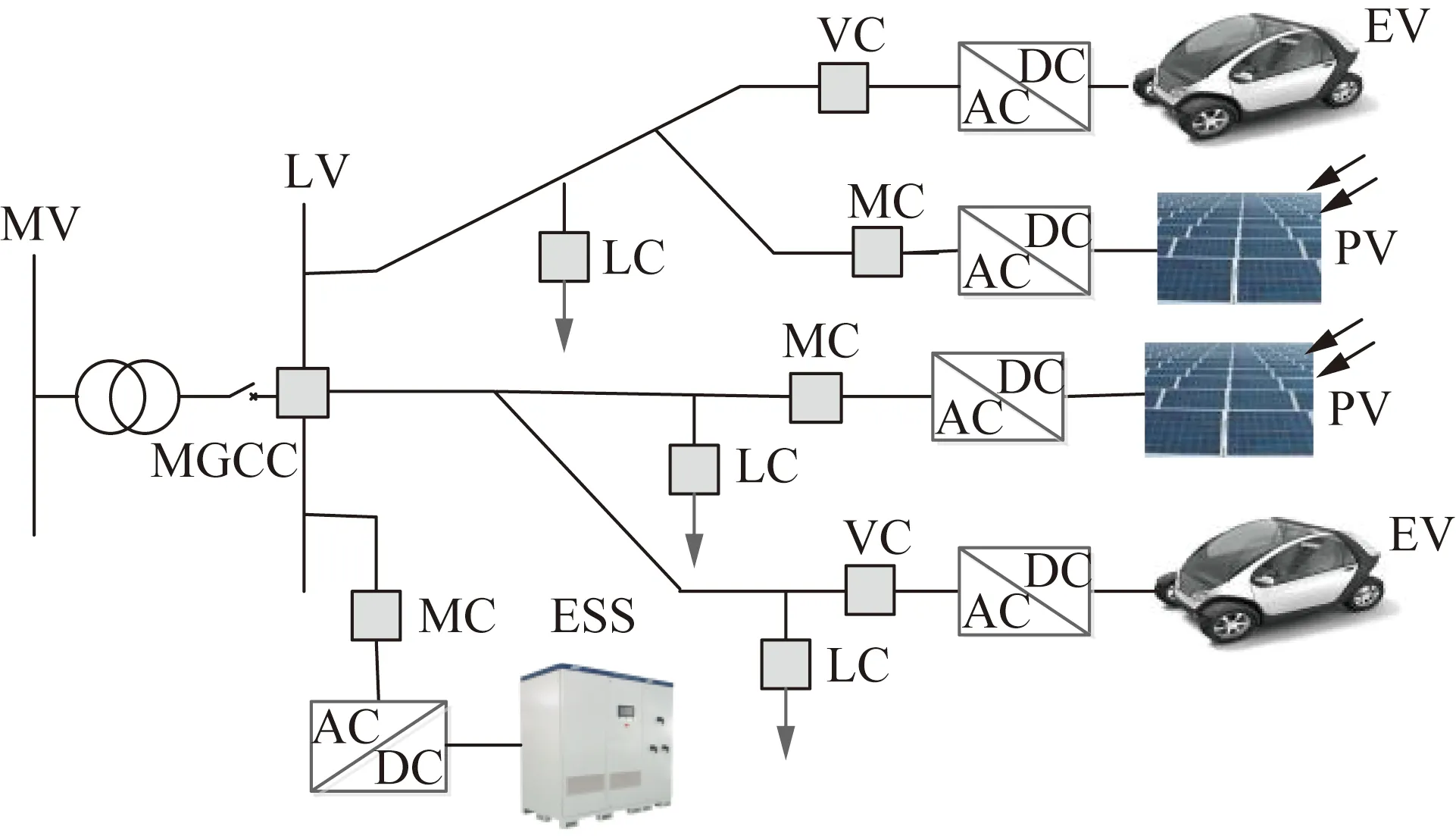
图1 CBMG结构及组成示意图

CBMG采用分层结构，由MGCC及其所控制的底层控制器构成。MGCC负责监测与协调微源与负荷的运行状态，是系统的最高管理层，具有协调所有资源的能力。在CBMG并网运行时，MGCC根据上层指令调整CBMG的电压、频率运行点；根据上层控制中心发出的模式切换指令，切换CBMG主要电源的控制模式。在CBMG孤岛运行时，根据本地负荷水平、PV及ESS的运行状态，协调CBMG微源的出力，维持CBMG的电压和频率水平。底层控制器会定期向MGCC输送功耗、发电量等信息，MGCC将会筛选和处理这些信息以实现对CBMG的管理[19]。

2 EEM策略

在配电网停电后，CBMG通过EEM策略对可控负荷投入量进行及时调整来减小停电给用户带来的损失、维持停电期间对重要负荷的供电。CBMG的能量管理控制框图如图2所示[20-21]。

EEM系统的输入端包含ESS实时运行状态、可控负荷可投入量、重要负荷实时数据及PV预测值[22]等信息；EEM系统的输出为EEM策略的优化方案，即可控负荷最优投入量。CBMG孤岛运行后，ESS作为主控单元采用U/f控制，可根据PV的出力大小与负荷的接入情况自动调整其充放电功率。图3是EEM策略的示意图。

图2 CBMG的能量管理控制框图

图3 EEM策略示意图

在计划停电时，EEM策略由优化模型与滚动优化策略构成。含有权重因子的优化模型，其优化目标兼顾减小停电损失与维持供电时间2个方面，约束条件考虑到功率平衡、可控负荷及ESS这3个方面。由于PV具有波动性与随机性，滚动优化策略[23]可通过不断更新PV预测值以减小PV预测误差对结果的影响。

在非计划停电时，由于停电持续时间未知，且ESS电量有限，应优先考虑对重要负荷的供电，在此基础上，尽可能地减小停电给用户带来的损失。以优先考虑对重要负荷供电为原则的实时应急方案，可根据每个时刻PV预测值的大小，动态决策该时刻可控负荷投入量。

2.1 计划停电

2.1.1 优化模型

在配电网停电后，EEM策略的优化模型既要考虑减小停电给用户带来的损失，又要顾及维持停电期间内对重要负荷的供电，因此在优化目标中引入了权重因子以权衡减小损失、维持供电二者的重要程度。其目标函数可描述为：

min αf(x)+βg(x)

(1)

(2)

(3)

式中：x为列向量，表示可控负荷投入量；f(x)表示可控负荷的相对改变量，f(x)越小，停电期间内可控负荷投入量越接近初始值，停电给用户带来的损失越小，并用权重因子α表示其重要性；g(x)表示可供电时长与停电时长的相对差值，g(x)越小，可供电时长越接近停电时长，越可以维持停电期间内对重要负荷的供电，并用权重因子β表示其重要性，权重因子α与β的和为1；i为优化次数；xci是第i次优化时可控负荷的投入量；xc0为停电发生时可控负荷的投入量；En为ESS的额定容量；eSOCi为第i次优化时ESS的荷电状态(state of charge，SOC)；eSOCmin为ESS的SOC下限值；Psdi为ESS在第i次优化时的放电功率；tb为计划停电时长；Δt为相邻2次优化的时间间隔。

在优化过程中，应满足下述约束条件。

(1)功率平衡的约束。在CBMG切换至孤岛运行后，ESS采用U/f控制，为维持系统的功率平衡，ESS的放电功率将满足式(4)，即

Pvi+Psdi=xci+xcri

(4)

式中：Pvi为第i次优化时PV的预测值；xcri为第i次优化的重要负荷投入量，是一个常数。由于PV预测值存在一定的误差，在实时应急过程中，若该误差在ESS的允许调节范围内，则由ESS平衡；否则，由可控负荷平衡；若可控负荷投入量为0时仍无法平衡，则需切掉部分重要负荷。

(2)可控负荷的约束。可控负荷应在一定范围内调节，可表示为：

xcmin≤xci≤xcmax

(5)

xcmin=Lcvmin+Lctmin+Lcrmin

(6)

xcmax=Lcvmax+Lctmax+Lcrmax

(7)

式中：xcmin，xcmax为xci的下限与上限；Lcvmin，Lctmin与Lcrmin是可控负荷EV、温控设备与次要照明设备的功率下限值；Lcvmax，Lctmax与Lcrmax是可控负荷EV、温控设备与次要照明设备的功率上限值。

(3)ESS的约束。为防止过充过放对ESS造成伤害，ESS的SOC应严格地控制在一定的范围内，可表示为

eSOCmin≤eSOCi≤eSOCmax

(8)

式中eSOCmax为eSOCi的上限值[24]。

在第i次优化时ESS中储存的能量也应在一定的范围内，可表示为

(9)

式中eSOC0为SOC的初始值。

此外，ESS的充放电功率也有范围限制，可表示为：

Pscmin≤Psci≤Pscmax

(10)

Psdmin≤Psdi≤Psdmax

(11)

式中：Psci为第i次优化时ESS的充电功率；Pscmax与Pscmin为ESS充电功率的上下限；Psdmax与Psdmin为ESS放电功率的上下限。

2.1.2 滚动优化策略

滚动优化策略通过不断更新PV的实时数据及其预测值，以减小预测误差所带来的影响。

滚动优化策略的流程图如图4所示，具体步骤列于下文。

图4 滚动优化策略流程图

(1)获取初始时刻t=t0时的基础数据，包括xc0，eSOC0及PV预测值。

(2)设定n′为滚动优化策略执行的次数，T为计划停电时相邻2次滚动优化的时间间隔。根据优化模型，获取停电t=(n′-1)T至t=tb时间段内的可控负荷投入量。

(3)若tb≥n′T，则停电未恢复，在t=(n′-1)T到t=n′T时间段内，按照步骤(2)的结果实施优化方案；若(n′-1)T≤tb

(4)计算ESS的剩余电量，判定在t=t0+T时是否能保证功率平衡，若无法保持平衡，跳出循环。

(5)更新t0值，使得t0=t0+T。

(6)补充PV在t=t0-T到t=t0时间段内的实际出力值以更新PV实时数据，并更新PV预测值。

(7)返回步骤(1)。

2.2 非计划停电

在非计划停电时，由于停电持续时间未知，且ESS电量有限，应优先考虑对重要负荷的供电，则须减少可控负荷投入量以使得ESS保留足够电量。在配电网停电后，根据每个时刻PV预测值的大小制定实时应急方案，动态决策可控负荷投入量，由于ESS采用U/f控制，可自动调节其充放电功率以维持系统功率平衡。

设定在第j个时刻，PV预测值、重要负荷、可控负荷投入量分别为Pvj,xcrj,xcj，可控负荷投入量最大值为xcmax，ESS最大充放电功率为分别为Pscmax,Psdmax。实时应急方案如图5所示，具体策略如下。

图5 实时应急方案示意图

(1)若Pvj≥xcrj+xcmax+Pscmax，则光伏功率过剩，可控负荷全部投入，MGCC限制光伏出力为Pvj=xcrj+xcmax+Pscmax。

(2)若xcrj+Pscmax≤Pvj

(3)若xcrj-Psdmax≤Pvj

(4)若Pvj

3 计划停电下的算例分析

3.1 参数设置

设定配电网计划停电1 h，发生在下午15:00—16:00。在CBMG中，PV装机容量为100 kW，ESS额定容量为50 kW·h。

考虑到重要负荷xcr与可控负荷最大值xcmax存在一定的波动性，xcr在18 kW到42 kW间随机生成，xcmax在80 kW到112 kW间随机生成，如图6所示。其他参数设置如表1所示。

图6 随机生成的xcr与xcmax示意图

3.2 对比分析

为更好地验证计划停电下EEM策略的有效性，本文采用了对比分析。当采用传统策略时，由于计划停电的停电时长已知，若CBMG的微源出力无法满足所有负荷的需求，为充分利用ESS的备用能量，可将其在停电期间内予以平均分配以使得ESS在每个时刻的备用作用是相同的，并由式(4)计算可控负荷投入量，则ESS在停电期间的放电功率为

(12)

而EEM策略将根据优化模型与滚动优化策略及时调整可控负荷投入量。由于ESS采用U/f控制，其充放电功率可自动调节。

算例1：采用传统策略。算例结果如图7所示。

算例2：采用EEM策略。设定权重因子α为0.9，β为0.1，算例结果如图8所示。

算例3：采用EEM策略。设定权重因子α为0.1，β为0.9，算例结果如图9所示。

图7 传统策略算例结果(计划停电)

在算例1中，ESS恒以10 kW的功率放电，若计划停电发生在更晚的时间，PV出力的减小很可能会出现微源出力不足而无法满足重要负荷需求的情况，这将给CBMG的可靠运行带来隐患。此外，传统策略下可控负荷投入量的方差为12.8，波动较大，可控负荷运行状态的变化幅度较大，这也在一定程度上影响了设备的使用，降低了用户满意度。

图8 EEM策略算例结果(α=0.9, β=0.1)

图9 EEM策略算例结果(α=0.1, β=0.9)

而在算例2与算例3中，根据EEM策略决策可控负荷投入量，且ESS的放电功率也不再是恒定值。在停电初期，PV出力值较大，ESS以较小的功率放电，甚至是充电，这将有利于ESS留有更多的电量以维持后期对重要负荷的供电。随着时间的推移，PV出力值逐渐减小，ESS放电功率的增加不仅可以维持对重要负荷的供电，也有利于更多的可控负荷接入CBMG，从而减小停电给用户带来的损失。因此在计划停电期间，SOC曲线的走势由缓至陡。此外，在算例2与算例3中，可控负荷投入量的方差分别为7.9和10.7，二者均小于12.8，可见其波动较小。

由算例结果对比分析可知，EEM策略可根据PV与重要负荷的波动情况对可控负荷投入量进行有效的调节。

3.3 灵敏度分析

权重因子α、β分别表示减小损失与维持供电二者的重要程度，权重因子的改变将直接影响优化结果。图10为α=0.1、β=0.9，α=0.2、β=0.8，α=0.9、β=0.1，3种情况下ESS的SOC变化图。

图10 权重因子改变时SOC变化图

当β较大时，维持对重要负荷的供电较为重要，在停电初期PV出力较大时，应尽量减小ESS放电功率，因此相应的SOC值较大。当α的值增大，减小停电损失的重要性有所提高，因此ESS放电功率增大，SOC相应地减小。由于要维持停电期间内对重要负荷的供电，又要兼顾减小停电损失，应充分利用ESS的备用资源，因此停电结束时，ESS的SOC降至下限值。

图11与图12给出了α从0.1增至0.9，β从0.9降至0.1时，相应的f(x)与g(x)的变化情况。权重因子α越大，减小停电损失越重要，用于表征该目标的f(x)的函数值越小。如图11所示，随着α的增大，f(x)呈现下降趋势。而权重因子β越小，越不利于维持负荷供电，用于表征该目标的g(x)的函数值越大。如图12所示，随着β的减小，g(x)呈现上升趋势。

由上述分析可知，不同的权重因子可灵活调节减小损失与维持供电在优化目标中的比重，进而影响停电期间内可控负荷投入量与ESS充放电功率。eSOC0越大，计划停电时间越短，越有利于维持对重要负荷的供电，此时可令权重因子α取某一较大值。在其他情况下，若用户对可控负荷的依赖度超过重要负荷的重要程度，如夏季空调温度不理想，即使系统能够正常运行也不能为用户创造良好的工作环境，此时应令权重因子α取较大值，β取较小值；否则，应令权重因子β取较大值，而α取较小值。可根据具体的场景或需求选择适宜的权重因子。

图11 权重因子改变时f(x)变化图

图12 权重因子改变时g(x)变化图

4 非计划停电下的算例分析

4.1 参数设置

设定配电网于下午15:00发生非计划停电。在15:00至16:00期间，PV出力、重要负荷、可控负荷最大值、ESS充放电功率上下限、PV装机容量及ESS额定容量均与计划停电下的算例数据相同。

4.2 对比分析

非计划停电时，传统策略的流程图如图13所示。与计划停电时的控制策略不同，由于非计划停电的停电时长未知，宜尽可能最大限度地让ESS出力以维持CBMG的可靠运行。图13中i为决策次数，xcei是第i次决策时可控负荷投入量的预估值。而EEM策略将根据实时应急方案及时调整可控负荷投入量。

图13 传统策略流程图

算例1：采用传统策略。停电1 h内的算例结果如图14所示。

图14 传统策略算例结果(非计划停电)

算例2：采用EEM策略，实时应急方案下的算例结果如图15所示。

在算例1中，由于采用传统控制策略，ESS在停电前期以较大的功率放电，其SOC下降较快。ESS的备用电量持续减小，且由于停电发生在下午，PV出力将随光照的减弱呈现下降趋势，这将不利于CBMG供电时间的延长。此外，约在停电40 min时，便出现部分重要负荷被切除的情况，这将严重影响系统的可靠运行。

图15 EEM策略算例结果(非计划停电)

而在算例2中，由于采用了实时应急方案，在停电初期PV出力较大时，ESS以较大的功率充电，这将有利于CBMG供电时间的延长。随着PV出力的减小，可控负荷投入量降为0，ESS放电功率的增加将有效维持对重要负荷的供电。在这60 min内，重要负荷始终全部接入，且在第60 min时，ESS的SOC约为0.7，为接下来重要负荷的供电提供了较为充足的备用电量。

由算例结果对比分析可知，EEM策略可根据PV与重要负荷的波动情况有效调节可控负荷投入量，以维持CBMG的可靠运行。

5 结 论

本文针对配电网停电情况下含有光储系统而不含柴油发电机组的CBMG，提出了一种考虑计划停电与非计划停电2种情况的EEM策略，以减小停电给用户带来的损失、维持停电期间内对重要负荷的供电。在计划停电时，EEM策略由优化模型与滚动优化策略构成。含有权重因子的优化模型，其优化目标兼顾减小停电损失与维持供电时间2个方面，并在算例中进行了灵敏度分析，不同的权重因子可灵活调节二者在优化目标中的比重，从而直接影响可控负荷投入量。滚动优化策略考虑了PV的波动性与随机性，通过不断更新PV预测值以减小预测误差所带来的影响。在非计划停电时，由于停电持续时间未知，且ESS电量有限，应优先考虑对重要负荷的供电，并以此为原则制定了实时应急方案，根据每个时刻PV预测值的大小动态决策可控负荷投入量。由计划停电条件下和非计划停电条件下的算例对比分析可知，EEM策略可通过有效调节可控负荷投入量来实现预期目标。

[1]鲁宗相, 王彩霞, 闵勇, 等. 微电网研究综述[J]. 电力系统自动化, 2007, 31(19): 100-107. LU Zongxiang, WANG Caixia, MIN Yong, et al. Overview on microgrid research[J]. Automation of Electric Power Systems,2007,31(19):100-107.

[2]解翔, 袁越, 李振杰. 含微电网的新型配电网供电可靠性分析[J]. 电力系统自动化, 2011, 35(9): 67-72. XIE Xiang, YUAN Yue, LI Zhenjie. Reliability analysis of a novel distribution network with micro-grid[J]. Automation of Electric Power Systems,2011,35(9):67-72.

[3]LIU N,TANG Q, ZHANG J, et al. A hybrid forecasting model with parameter optimization for short-term load forecasting of micro-grids[J]. Applied Energy, 2014(129): 336-345.

[4]WANG X, GUERRERO J M, BLAABJERG F, et al. A review of power electronics based microgrids[J]. Journal of Power Electronics, 2012, 12(1): 181-192.

[5]杨新法, 苏剑, 吕志鹏, 等. 微电网技术综述[J]. 中国电机工程学报,2014,34(1): 57-70. YANG Xinfa, SU Jian, LYU Zhipeng, et al. Overview on micro-grid technology[J]. Proceedings of the CSEE,2014,34(1): 57-70.

[6]李振杰, 袁越. 智能微网：未来智能配电网新的组织形式[J]. 电力系统自动化, 2009, 33(17): 42-48. LI Zhenjie, YUAN Yue. Smart microgrid: a novel organization form of smart distribution grid in the future[J]. Automation of Electric Power Systems, 2009, 33(17): 42-48.

[7]王兆宇, 艾芊. 基于QPSO与BPSO算法的动态微电网多目标优化自愈[J]. 电网技术, 2012, 36(10): 23-29. WANG Zhaoyu, AI Qian. Multi-objective optimal self-healing of dynamic microgrid based on quantum-based PSO and binary PSO[J]. Power System Technology, 2012, 36(10): 23-29.

[8]JANANI S, MUNIRAJ C. Fuzzy control strategy for microgrids islanded and grid connected operation[C]// 2014 International Conference on Green Computing Communication and Electrical Engineering (ICGCCEE). Coimbatore：IEEE，2014：1-6.

[9]GOUVEIA C, LEAL MOREIRA C, PECAS LOPES J A, et al. Microgrid service restoration: the role of plugged-in electric vehicles[J].Industrial Electronics Magazine, IEEE, 2013, 7(4): 26-41.

[10]王增平, 张丽, 徐玉琴, 等. 含分布式电源的配电网大面积断电供电恢复策略[J]. 中国电机工程学报, 2010,30(34): 8-14. WANG Zengping, ZHANG Li, XU Yuqin, et al. Service restoration strategy for blackout of distribution system with distributed generators[J]. Proceedings of the CSEE,2010,30(34):8-14.

[11]刘志文, 夏文波, 刘明波. 实现微网供电恢复的分布式电源自组网策略[J]. 电力系统自动化, 2015, 39(9): 192-199. LIU Zhiwen, XIA Wenbo, LIU Mingbo. Distributed generator self-organized network strategy applied to microgrid service restoration[J]. Automation of Electric Power Systems, 2015, 39(9): 192-199.

[12]OU T C, LIN W M, HUANG C H, et al. A hybrid programming for distribution reconfiguration of DC microgrid[C]//2009 IEEE PES/IAS Conference on Sustainable Alternative Energy (SAE). Valencia: IEEE, 2009:1-7.

[13]CHEN C, WANG J, QIU F, et al. Resilient distribution system by microgrids formation after natural disasters[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 958-966.

[14]MOHAGHEGHI S, YANG F. Applications of microgrids in distribution system service restoration[C]//Innovative Smart Grid Technologies (ISGT), 2011 IEEE PES. Hilton Anaheim, CA: IEEE, 2011: 1-7.

[15]郭力, 富晓鹏, 李霞林, 等. 独立交流微网中电池储能与柴油发电机的协调控制[J]. 中国电机工程学报, 2012, 32(25): 70-78. GUO Li, FU Xiaopeng, LI Xialin, et al. Coordinated control of battery storage and diesel generators in isolated AC microgrid systems[J]. Proceedings of the CSEE, 2012, 32(25): 70-78.

[16]成思琪, 刘俊勇, 向月, 等. 微网中混储/柴协调运行策略研究[J]. 电力系统保护与控制, 2015, 43(7): 42-50. CHENG Siqi, LIU Junyong, XIANG Yue, et al. Research on optimal coordinated operation for microgrid with hybrid energy storage and diesel generator[J]. Power System Protection and Control, 2015, 43(7): 42-50.

[17]LOPES J A P, POLENZ S A, MOREIRA C L, et al. Identification of control and management strategies for LV unbalanced microgrids with plugged-in electric vehicles[J]. Electric Power Systems Research, 2010, 80(8): 898-906.

[18]LIU N, CHEN Q, LU X, et al. A charging strategy for pv-based battery switch stations considering service availability and self-consumption of PV energy[J]. IEEE Transactions on Industrial Electronics, 2015, 62(8): 4878-4889.

[19]GOUVEIA C, MOREIRA J, MOREIRA C L, et al. Peças lopes, coordinating storage and demand response for microgrid emergency operation[J]. IEEE Transactions on Smart Grid,2013,4(4):1898-1908.

[20]MALYSZ P, SIROUSPOUR S, EMADI A. An optimal energy storage control strategy for grid-connected microgrids[J]. IEEE Transactions on Smart Grid,2014,5(4):1785-1796.

[21]MA L, LIU N, WANG L, et al. Multi-party energy management for smart building cluster with PV systems using automatic demand response[J]. Energy and Buildings, 2016(121): 11-21.

[22]刘念, 张清鑫, 李小芳. 基于核函数极限学习机的分布式光伏短期功率预测[J]. 农业工程学报, 2014, 30(4): 152-159. LIU Nian, ZHANG Qingxin, LI Xiaofang. Distributed photovoltaic short-term power output forecasting based on extreme learning machine with kernel[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(4): 152-159.

[23]PALMA-BEHNKE R, BENAVIDES C, LANAS F, et al. A microgrid energy management system based on the rolling horizon strategy[J]. IEEE Transactions on Smart Grid, 2013, 4(2): 996-1006.

[24]谭兴国, 王辉, 张黎, 等. 微电网复合储能多目标优化配置方法及评价指标[J]. 电力系统自动化, 2014, 38(8): 7-14. TAN Xingguo, WANG Hui, ZHANG Li, et al. Multi-objective optimization of hybrid energy storage and assessment indices in microgrid[J]. Automation of Electric Power Systems, 2014, 38(8): 7-14.

(编辑 张媛媛)

Emergency Energy Management Strategy for Commercial Building Microgrid

CUI Yi, LIU Nian, CHEN Qifang

(State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China)

When there is a power failure in distribution network, commercial building microgrid can be operated autonomously. In order to reduce the users’ loss caused by power outage and preserve the power supply of important loads during blackout, this paper presents a novel emergency energy management strategy for commercial building microgrid with photovoltaic-battery system, where planned and unplanned outages are both taken into account. When the outage is planned, an optimization model is established, aiming to reduce outage loss and preserve power, and weighting factors are introduced to weigh the importance of reducing loss and preserving power. Rolling optimization strategy is proposed to reduce the prediction errors on the result. When the outage is unplanned, a real-time emergency program is established, following the principle of giving priority to preserve the power supply of important loads. Comprehensive results obtained from comparison simulations show that the proposed strategy is efficacious in adjusting the input of controllable loads to reach the desired goals. Additionally, sensitivity analysis is carried out in case study section, and different weighting factors will flexibly adjust the importance of reducing outage loss and preserving power in the optimization goal.

planned/unplanned outage; emergency energy management; rolling optimization strategy; commercial building microgrid; microgrid

国家高技术研究发展计划项目(863计划) (2014AA052001)

TM 76

A

1000-7229(2016)10-0024-09

10.3969/j.issn.1000-7229.2016.10.004

2016-06-28

崔仪(1992)，女，硕士研究生，研究方向为微电网能量管理；

刘念(1981)，男，博士，副教授，主要研究方向为新能源与智能配用电系统、电力系统信息安全等；

陈奇芳(1986)，男，博士研究生，研究方向为智能配用电与微电网、电动汽车。

Project supported by the National High Technology Research and Development of China (863 Program) (2014AA052001)