考虑需求响应的有源配电系统可靠性评估

胡美玉，胡志坚

(武汉大学电气工程学院，武汉市 430072)

考虑需求响应的有源配电系统可靠性评估

胡美玉，胡志坚

(武汉大学电气工程学院，武汉市 430072)

提出一种考虑需求响应(demand response，DR)的配电系统可靠性评估算法。首先采用改进隶属度函数进行峰谷时段划分，并建立综合分时电价和激励机制的用户响应模型。为提高可靠性评估效率，提出基于阈值和最小距离的聚类方法产生年负荷的多状态模型。计及风力发电机出力的相关性，利用秩相关系数、拉丁超立方抽样和Cholesky分解获取风机输出功率的相关性样本。在此基础上，通过修正孤岛稳定运行概率对传统可靠性指标的影响,可实现考虑负荷响应的有源配电网可靠性分析。应用所述的方法对算例进行可靠性评估，结果表明需求响应策略能改善电网可靠性和提高电能利用率。

需求响应(DR)；风力发电机；相关性；配电网；可靠性评估

0 引 言

需求响应(demand response，DR)是指电力用户根据价格信号或激励机制做出响应，改变固有习惯用电模式的行为[1]。在电力市场竞争中引入需求响应，可以引导用户参与到电力系统的削峰填谷行为中，改善负荷曲线，从而实现与风电出力互补，平缓风电的随机性和波动性给供电可靠性带来的影响，提高新能源的接纳能力[2-3]。

国内外已有大量学者对需求响应展开研究[4-6]，但是大多数集中在需求响应的经济效益或者系统备用配置优化，对配电系统可靠性[7-8]影响的研究较少。文献[9]提出了一种考虑分时电价的智能配电系统可靠性评估算法，但只考虑单一负荷水平，计算精度不高。在此基础上，文献[10]采用基于二分法的聚类负荷[11]分析对年负荷曲线进行分级划分，将各级负荷水平下的可靠性指标进行加权平均，提高了可靠性评估的精度。但仍存在以下问题：基于二分法的聚类模型按照位置间隔选取初始聚类中心，可能导致初始聚类中心恰好落在目标函数的局部最优值附近，使算法收敛到局部；需进行多次聚类，不利于可靠性指标的快速计算；仅仅针对需求响应中的电价机制；并未考虑分布式电源出力的间歇性与相关性。

事实上，需求响应措施按照用户的响应方式可划分为基于价格的需求响应和基于激励的需求响应[12]。并且随着分布式电源的大量接入，同一地理位置不同类发电系统间或不同地理位置同类发电系统间均具有相关性[13]。

本文将建立一种考虑需求响应和相关性的可靠性评估算法。采用改进隶属度函数进行峰谷时段划分，以解决峰谷区间临界点难以合理确定的问题。综合考虑分时电价和激励机制的影响，建立用户响应模型。提出基于阈值和最小距离的聚类方法获得年负荷多状态模型，并避免多次聚类。利用秩相关系数，拉丁超立方抽样和Cholesky分解产生风机出力的相关性样本。结合孤岛运行概率，修正孤岛运行对传统可靠性指标的影响进行考虑需求响应的有源配电网可靠性评估，最后通过算例仿真验证所提方法的可行性和有效性。

1 用户响应模型

1.1 时段划分

实施需求响应的主要目的就是通过用户调整用电负荷和用电时间，实现削峰填谷，平缓电力负荷曲线。负荷曲线上各点处于峰时段或谷时段的可能性可采用半梯形隶属函数确定[14]。其中采用偏小型半梯形隶属度函数来确定各时间点处于谷时段的可能性为A，偏大型半梯形隶属度函数来确定各时间点处于峰时段的可能性为B。

(1)

(2)

式中：a为各时间点负荷集合的最小值；b为各时间点负荷集合的最大值；qi为时间点i对应的负荷值。

取70%作为划分标准，得到峰、谷、平时段对应的时间点数量分别为n1、n2、24-n1-n2。为合理确定峰谷区间临界点的问题，采用2个修正策略[15]：各时段的时间点数量应控制在6～10个，并且峰时段数量不超过8个；每个时段不小于2 h[14]，将孤立时间点归并至相邻时间点集合，或者将相邻时间点归并至孤立时间点集合。采用显著性指标S计算分类效果，S越大，分类效果越好。

(3)

(4)

式中：Q1—Q3分别表示峰平谷时段的负荷集合。Qni、Qnk为负荷集合Qn中任意2个不同的负荷值。

1.2 需求响应效果测算模型

分时电价与激励机制的引入导致用户主动降低用电量，采用需求价格弹性来定量表征电力价格变化对用户行为特性的影响。

(5)

式中：ρ表示电价；d表示电量。

需求价格弹性E(i,k)描述了时刻i的电力需求量的变化率与时刻k的电价变化率之间的关系。有些时间点对应的负荷并不能向其他时间点转移，这些负荷的弹性值为负，称为“自弹性系数”；有些时间点的负荷能向其他时间点转移，这些负荷的弹性值为正，称为“交叉弹性系数”。

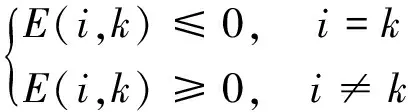
(6)

设引入需求响应后，i时刻用户用电量由d0(i)变化为d(i)，则负荷改变量如式(7)所示。

Δd(i)=d(i)-d0(i)

(7)

设i时刻用户削减单位负荷获得的奖励为Ci；电力系统出现容量短缺时，用户义务减少的电力负荷为IC(i)；削减量不足IC(i)的部分，单位负荷的惩罚为Di。用户获得的奖励和惩罚分别为：

IN(i)=CiΔd(i)

(8)

PEN(i)=Di·[IC(i)-Δd(i)]

(9)

假设H(i)为i时刻用户使用电量为d(i)下的收益，则用户总收益G可表示为

G=H(i)-d(i)ρ(i)+IC(i)-PEN(i)

(10)

为实现用户总收益最大，采用总收益G对电量d(i)求一次导数，并令倒数值为0。

(11)

用户在i时刻的收益与电量以及电价的关系可表示为[16]

(12)

等式两边同时对电量d(i)求一次导数，需求响应引起的时刻i的负荷变化量如式(13)所示。

(13)

式中Δρ(i)=ρ(i)-ρ0(i)，表示引入需求响应时刻i的电价变化。

以上分析仅仅针对单时刻点电价和激励对负荷的影响，根据电力需求量变化率与电价变化率之间的线性关系，可得多时刻点负荷响应模型为

(14)

2 负荷聚类

年负荷曲线由全年各个时间点对应的负荷值组成，其包含的负荷水平过多不易于直接应用于配电系统可靠性评估，通常采用聚类技术将年负荷曲线中的负荷值划分为多个等级。聚类技术的难点在于合理确定最优分级方案，使得同一负荷族中的负荷值尽可能具有相似性，而不同负荷族之间尽可能具有差异性。设负荷集合为Q={q1,q2,…,qn}，基于阈值和最小距离的聚类方法具体步骤如下：

步骤1：对负荷集合Q按照由小到大排序，将相同负荷值的负荷点进行合并，形成数组L(长度为Length),用数组Num存储各个负荷值被合并的负荷点个数；

步骤2：计算L中相邻负荷值的距离，并设定负荷距离阈值T：

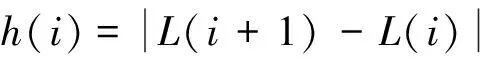
(15)

(16)

步骤3：将距离最近的一对负荷值归为第一类CL1；

步骤4：将负荷集合中与负荷类CLi中任意负荷值的距离小于T的负荷归并至CLi中；

步骤5：计算剩余负荷的最小距离hm，若hm小于T,则将该对负荷值归为一类，转向步骤4，否则转向步骤6；

步骤6：将该对负荷作为两类，转向步骤5；

步骤7：若最后一轮只剩1个负荷值，则将这个负荷值单独定为一类。

上述聚类过程不需要人为选取初始聚类中心和负荷级数，只需根据年负荷的实际分布情况，将距离小于负荷距离阈值的负荷全部归为一类。并可通过调整负荷阈值来增加或减小负荷级数，以满足实际的精度或计算效率的需要。

设聚类结束后，第i个负荷族的负荷值、负荷点数目、概率分别为Qci、NLdi和PLi。

(17)

(18)

PLi=NLdi/N

(19)

式中：Ic为负荷族i中的负荷点集合；N为负荷点总数。

为评价分级聚类效果，引入基于负荷族内和负荷族间距离的有效性指标Val，设分级聚类个数为M。

(20)

同一负荷族内的负荷距离越小，不同负荷族之间的距离越大，有效性指标越小，分级聚类效果越好。

3 风机出力的相关性样本

大量研究表明，风速服从威布尔分布，风机输出功率与风速为非线性关系[17-18]。当计及相关性时，风机出力服从相关非正态分布，而当前没有适用于相关非正态分布的直接抽样方法。秩相关系数是随机变量排列后的秩的Pearson相关系数，能较好地描述非正态分布随机变量的非线性相关关系。拉丁超立方抽样(Latin hypercube sampling，LHS)[19-20]是一种分层抽样技术，能使抽样点尽可能覆盖整个分布区间，提高抽样精度和效率。Cholesky分解是应用于LHS的排列方法，可以消除由于样本随机排列产生的相关性。结合秩相关系数、拉丁超立方抽样和Cholesky分解可获得与目标秩相关系数一致的相关性风速样本，具体过程如下。

(1)结合风速的历史样本数据，计算不同风电场所在地区的风速的目标秩相关系数矩阵ρso=(ρij)。

(21)

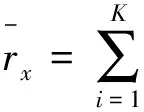
(2)设随机变量数为M1，采样规模为N1，生成M1×N1阶顺序矩阵R，每一行均为1,2,…,N1组成的随机整数序列；按照公式(21)计算R的秩相关系数矩阵ρsR。

(3)将随机变量m的累积概率等分为N1个等概率区间[(i-1)/N,i/N]，其中i的取值为顺序矩阵R的第m行，随机抽取区间中的一个值pi。

(22)

式中r为[0,1]均匀分布的随机数。

(4)对威布尔分布函数进行逆变换，得到区间[(i-1)/N,i/N]对应的采样值vi=F-1(pi)，最终可得M1×N1阶初始样本矩阵S。

(5)为消除因矩阵R各行随机排列产生的相关性，对ρsR进行Cholesky分解，P为其分解得到的下三角矩阵；按照公式(24)计算矩阵G，其秩相关系数矩阵为单位矩阵。

ρsR=PPT

(23)

G=P-1R

(24)

(6)对目标秩相关系数矩阵ρso进行Cholesky分解，Q为其分解后的下三角矩阵；将矩阵G更新为矩阵Gu，Gu的秩相关系数矩阵与ρso相等。

ρso=QQT

(25)

Gu=QG=QP-1R

(26)

(7)更新顺序矩阵R为Ru，使得Ru各行排列顺序与Gu一致。

(8)更新初始样本矩阵S为Su，使得Su各行排列顺序与Ru一致；Su即为秩相关系数矩阵与ρso近似相等的N1状态相关性风速样本空间。

根据风电机组出力和相关性样本Su中风速的关系，即可得到风力发电机(wind turbines generator，WTG)的输出功率。

4 计及负荷响应和相关性的可靠性评估

不同季节的负荷用电具有明显的季节性特征，因此峰谷时段划分也会有所不同。简单采用典型日负荷曲线来代替1年的负荷曲线进行分析，会带来较大误差。本文对每个季节进行峰谷时段划分，并逐一修正需求响应给年负荷曲线中的日负荷分布带来的影响，然后对修正后的年负荷曲线进行聚类分析。

DG接入配电网可以在主网正常时，与主电源一起给负荷供电；也可以在主网故障时，与主电网分离，向其所在的独立配电网供电。但是受风速随机性的影响，WTG的输出功率具有波动性和间歇性。当WTG的输出功率小于负荷需求时，孤岛不能形成，导致能源利用率不高。需求响应的采用能有效缓解由于间歇性可再生能源带来的电力供需矛盾，并且其成本只有储能装置的10%[1]。根据上文中聚类得到的多级负荷水平和WTG的相关性样本，可计算孤岛运行的概率PIS如下：

(27)

式中：∑PDGi,∑Qcj分别为同一孤岛内DG总出力和总负荷；∑PDGi≥∑Qcj成立时，p{·}为该状态DG出力对应的概率，否则p{·}为0。

与传统可靠性评估相比，DG的接入能在上游主馈线故障时，继续给孤岛内的负荷供电。为使紧急情况下的故障恢复供电有序进行，孤岛应当有计划地建立。因此孤岛外的负荷可靠性与孤岛的形成与否并没有关系，仍然可按照传统可靠性评估模型得到。

设LP为孤岛内的负荷，λ1、U1分别为DG接入前LP的故障率和年平均故障时间，PIS为孤岛稳定运行的概率，λ2、U2分别为DG接入后LP的故障率和年平均故障时间，则孤岛内负荷的可靠性指标计算如下：

λ3=(1-PIS)λ1+PISλ2=λ1-PIS(λ1-λ2)

(28)

U3=(1-PIS)U1+PISU2=U1-PIS(U1-U2)

(29)

认为DG在孤岛形成前后可以连续给孤岛内负荷供电，有无DG时LP的可靠性指标的差别只取决于其上游主馈线元件故障参数以及孤岛稳定运行的概率PISi，如式(30)—(31)所示。

(30)

(31)

式中m、λki、Uki分别为孤岛上游主馈线元件的个数、故障率、年平均故障时间。

上述分析并未考虑通过削减负荷实现当孤岛内DG出力不足时的剩余负荷的正常供电。因此，需要对此种情况下的正常供电负荷的可靠性进行补偿。

(32)

(33)

式中：PCi为实行切负荷策略下负荷i恢复供电的概率；λ4、U4分别为考虑切负荷策略后的负荷故障率和年平均故障时间。

综合负荷重要程度以及位置因素确定负荷削减的优先顺序，定义负荷削减系数为IL。

ILi=αLi+βLi

(34)

式中：αLi为负荷的重要程度系数；βLi为负荷与孤岛电源之间的电气距离，即负荷与孤岛电源之间的负荷个数(包含该负荷)。

5 算例分析

5.1 算例数据

为了验证本文所提方法和模型的有效性，以改进IEEE RBTS BUS6主馈线F4为基础，在分支线53、59处加入2个WTG，如图1所示。该系统包括30条线路、23个负荷点、23个配电变压器及熔断器、4台断路器和9台分段开关。所有负荷的年负荷曲线均采用IEEE-RTS79负荷百分比模型，负荷峰值以及元件可靠性参数参见文献[20]。

设隔离开关和联络开关的切换时间均为1 h，LHS采样规模为 1 000，WTG的额定功率为 1.2 MW，威布尔分布的形状参数为3.97，尺度参数为10.7；切入风速为3 m/s，额定风速为14 m/s，切除风速为25 m/s。负荷重要程度系数：工商业为1.2，农业为1.1，居民用户为1.0。

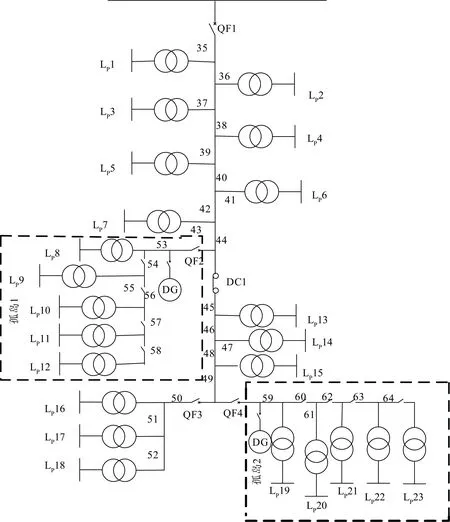
图1 IEEE RBTS BUS6系统接线图

5.2 需求响应效果

虽然不同季节的峰谷时段不同，但是计算过程相同。不同季节的峰谷时段划分结果如表1所示。

表1 不同季节时段划分结果

Table 1 Results of different seasons’ time period partition

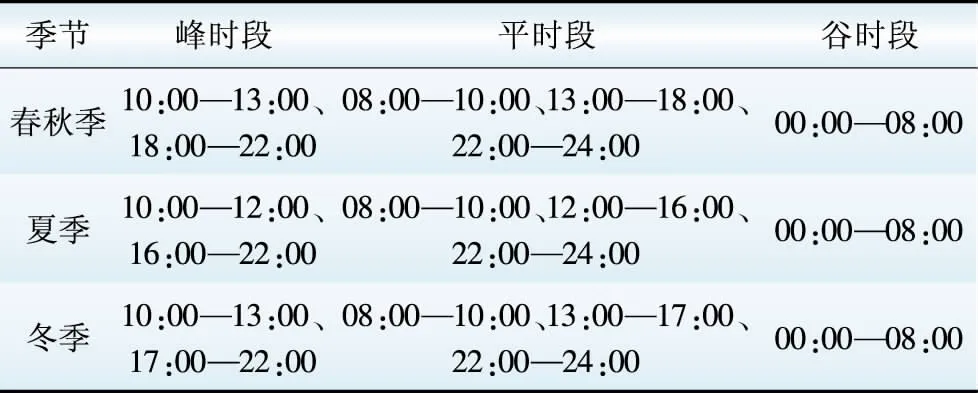
引入需求响应前的电价为0.7元/(kW·h)，峰、平、谷时段的电价分别为1.00，0.75，0.20元/(kW·h)；激励与惩罚均为0.10元/(kW·h)，需求价格弹性系数矩阵为

计算只采用电价机制(情景2)和综合采用电价与激励机制(情景3)后的负荷分布，并与引入需求响应前的典型日负荷曲线(情景1)比较，如图2所示。可以看出，分时电价的实施可有效改善负荷曲线，实现削峰填谷；综合电价机制与激励机制可使得负荷曲线更加平缓，改善效果更佳。

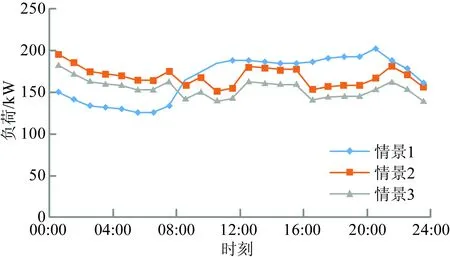
图2 不同情景下的典型日负荷曲线

5.3 可靠性评估

将5.2节情景3的负荷曲线进行聚类，最终得到的负荷分级数为750，有效性指标为0.110 7。负荷类内距离远小于负荷类间距离，说明聚类效果较好。由于分类数太多，在此不列出详细的计算结果。

采用本文算法分别针对以下4种方案进行可靠性计算。方案1：未接入DG，不考虑需求响应；方案2：接入DG，不考虑需求响应；方案3：接入DG，只考虑电价机制；方案4：接入DG，同时考虑电价和激励机制。部分负荷的可靠性指标如表2所示，系统可靠性指标如表3所示。

表2 部分负荷点可靠性指标

Table 2 Part load point reliability indices

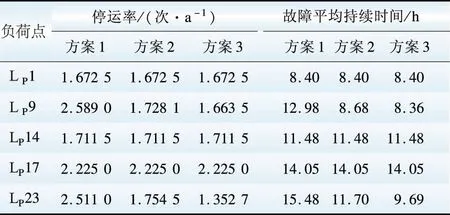
表3 系统可靠性指标

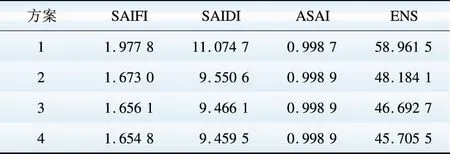
由表2和表3的计算结果可知，接入分布式电源能改善孤岛内负荷的停电时间和停电次数，如LP9和LP23，可以在总体上改善系统可靠性。比较方案2和方案3的可靠性指标可见，引入需求响应后，系统的年平均停电次数和停电时间得到进一步减小，说明了需求响应在平缓新能源出力波动和提高能源利用率方面的作用。与方案3相比，方案4的SAIFI、SAIDI、ENS指标更小，系统可靠性更高，说明综合考虑各种需求响应措施，可以更有效地减小负荷曲线的峰值，从而缓解由于间歇性可再生能源带来的电力供需矛盾，提高配电系统的供电可靠性。

6 结 论

(1)基于改进隶属度函数的峰谷时段划分模型，通过设定显著性指标和修正策略，能合理确定峰谷区间的临界点。

(2)提出了基于阈值和最小距离的聚类方法，无须人为选取初始聚类中心和负荷级数，并可通过调整负荷阈值来增加或减小负荷级数，以满足实际的精度或计算效率的需要。

(3)DG接入有利于改善配电系统的可靠性，需求响应的实施可有效改善负荷峰谷差和平缓风电功率的波动性，能进一步提高供电可靠性。

(4)综合电价机制和激励机制能使负荷曲线的改善效果更佳；可见同时实施多种策略能更有效引导用户参与到电力系统的削峰填谷，大大降低电力系统的运行风险。

[1]田世明, 王蓓蓓, 张晶. 智能电网条件下的需求响应关键技术[J]. 中国电机工程学报,2014, 34(22): 3576-3589.

TIAN Shiming, WANG Beibei, ZHANG Jing. Key technologies for demand response in smart grid[J]. Proceedings of the CSEE,2014, 34(22): 3576-3589.

[2]MOURA P S, ALMEIDA A T D. The role of demand-side management in the grid integration of wind power[J]. Applied Energy, 2010, 87(8):2581-2588.

[3]胡美玉, 胡志坚, 史梦梦. 基于改进粒子群优化算法的DG准入容量与优化布置[J]. 电力建设,2014, 35(12): 111-115.

HU Meiyu, HU Zhijian, SHI Mengmeng. Penetration level and optimize layout of distributed generation based on improved particle swarm optimization algorithm[J]. Electric Power Construction,2014, 35(12): 111-115.

[4]刘小聪, 王蓓蓓, 李扬, 等. 基于实时电价的大规模风电消纳机组组合和经济调度模型[J]. 电网技术,2014, 38(11): 2955-2963.

LIU Xiaocong, WANG Beibei, LI Yang,et al. Unit commitment model and economic dispatch model based on real time pricing for large-scale wind power accommodation[J]. Power System Technology,2014, 38(11): 2955-2963.

[5]包宇庆, 李扬, 王春宁, 等. 需求响应参与大规模风电接入下的电力系统频率调节研究[J]. 电力系统保护与控制,2015, 45(4): 32-37.

BAO Yuqing, LI Yang, WANG Chunning,et al. On demand response participating in the frequency control of the grid under high wind penetration[J]. Power System Protection and Control,2015, 45(4): 32-37.

[6]张颖, 容展鹏, 张宇雄, 等. 基于微电网的电网需求响应研究[J]. 电力系统保护与控制,2015, 43(21): 20-26.

ZHANG Ying, RONG Zhanpeng, ZHANG Yuxiong,et al. Study of grid demand response based on micro grid[J]. Power System Protection and Control,2015, 43(21): 20-26.

[7]胡美玉, 胡志坚, 邓奥攀, 等. 基于元件层级和电源可达性的配电网可靠性评估混合算法[J]. 电力系统保护与控制,2016, 44(8): 22-29.

HU Meiyu, HU Zhijian, DENG Aopan,et al. Hybrid algorithm for reliability evaluation of distribution network based on element hierarchy and power accessibility[J]. Power System Protection and Control,2016, 44(8): 22-29.

[8]胡美玉, 胡志坚, 汪祥, 等. 基于双向层级结构的计及开关故障的配电系统可靠性评估[J]. 电网技术,2016, 40(5): 1476-1481.

HU Meiyu, HU Zhijian, WANG Xiang,et al. Reliability evaluation of distribution network taking switch faults into account based on bidirectional hierarchical structure[J]. Power System Technology,2016, 40(5): 1476-1481.

[9]谢海鹏, 别朝红, 华博文, 等. 考虑分时电价的智能配电系统可靠性评估[EB/OL].(2013-01-09) [2016-07-22]. http:/www.paper.edu.cn/releasepaper/content/201301-445.

[10]赵洪山, 王莹莹, 陈松. 需求响应对配电网供电可靠性的影响[J]. 电力系统自动化,2015, 39(17): 49-55.

ZHAO Hongshan, WANG Yingying, CHEN Song. Impact of demand respond on distribution system reliability[J]. Automation of Electric Power Systems,2015, 39(17): 49-55.

[11]鲁国起, 张轶, 张焰, 等. 基于二分法的聚类负荷模型及其在电力系统可靠性评估中的应用[J]. 电力系统保护与控制,2011, 39(10): 31-36.

LU Guoqi, ZHANG Yi, ZHANG Yan,et al. Clustering load model based on the dichotomy and its application in power system reliability evaluation[J]. Power System Protection and Control,2011, 39(10): 31-36.

[12]KIRSCHEN D S, STRBAC G, CUMPERAYOT P,et al. Factoring the elasticity of demand in electricity prices[J]. IEEE Transactions on Power Systems, 2000, 15(2):612-617.

[13]胡美玉, 胡志坚, 胡梦月. 计及相关性的含分布式电源配电系统可靠性评估[J]. 电力建设,2016, 37(9): 108-114.

HU Meiyu, HU Zhijian, HU Mengyue.Reliability evaluation of distribution network with distributed generation considering correlations[J]. Electric Power Construction,2016, 37(9): 108-114.

[14]丁宁, 吴军基, 邹云. 基于DSM的峰谷时段划分及分时电价研究[J]. 电力系统自动化,2001, 25(23): 9-12.

DING Ning, WU Junji, ZOU Yun. Research of peak and valley time period partition approach and TOU price on DSM[J]. Automation of Electric Power Systems,2001, 25(23): 9-12.

[15]连振洲, 温步瀛, 江岳文. 基于负荷曲线分布特征的峰谷时段划分和修正策略研究[J]. 电网与清洁能源,2014, 30(7): 15-19.

LIAN Zhenzhou, WEN Buying, JIANG Yuewen. Peak-valley time period partition and correction strategy based on the load curve distribution[J]. Power System and Clean Energy,2014, 30(7): 15-19.

[16]AALAMI H A, MOGHADDAM M P, YOUSEFI G R. Demand response modeling considering interruptible/curtailable loads and capacity market programs[J]. Applied Energy, 2010, 87(1):243-250.

[17]ZHANG Shenxi, CHENG Haozhong, ZHANG Libo,et al. Probabilistic evaluation of available load supply capability for distribution system[J]. IEEE Transactions on Power Systems, 2013, 28(3):3215-3225.

[18]王彤, 卢斯煜, 金小明, 等. 风电并网对南方电网可靠性的影响评估[J]. 电力建设,2015,36(10): 161-166.

WANG Tong, LU Siyu, JIN Xiaoming,et al. Influence assessment of wind power integration on China southern power gridreliability[J]. Electric Power Construction,2015,36(10): 161-166.

[19]张巍峰, 车延博, 刘阳升. 电力系统可靠性评估中的改进拉丁超立方抽样方法[J]. 电力系统自动化,2015, 39(4): 52-57.

ZHANG Weifeng, CHE Yanbo, LIU Yangsheng. Improved Latin hypercube sampling method for reliability evaluation of power systems[J]. Automation of Electric Power Systems,2015, 39(4): 52-57.

[20]BILLINTON R, JONNAVITHULA S. A test system for teaching overall power system reliability assessment[J]. IEEE Transactions on Power Systems, 1996, 11(4):1670-1676.

(编辑 刘文莹)

An Active Distribution System Reliability Evaluation Method Considering Demand Response

HU Meiyu, HU Zhijian

(School of Electrical Engineering, Wuhan University, Wuhan 430072, China)

This paper proposes a new reliability evaluation method for distribution system considering demand response. Firstly, we divided the peak-valley periods based on improved membership function and established a customer response model integrating time-of-use price and incentives. To improve the reliability assessment efficiency, a clustering method based on threshold and minimum distance was proposed to generate annual load multi-state model. We applied the correlation coefficient matrix, Latin hypercube sampling and Cholesky decomposition to get the correlation sample of wind turbine generator output. Finally, the reliability analysis of active distribution network considering demand response can be realized by correcting the traditional reliability index based on island stable operation probability. Applying the proposed method to the reliability evaluation of example, the results show that the demand response strategy can improve the reliability and energy efficiency of grid.

demand response(DR); wind turbine generator; correlations; distribution network; reliability evaluation

高等学校博士学科点专项科研基金项目(20110141110032)

TM 72

A

1000-7229(2016)12-0112-07

10.3969/j.issn.1000-7229.2016.12.015

2016-08-09

胡美玉(1990)，女，硕士研究生，主要从事电力系统可靠性分析、含DG的配电网优化运行的研究工作；

胡志坚(1969)，男，通信作者，博士，教授，博士生导师，研究方向为电力系统稳定分析与控制、新能源与分布式发电。