改进Sammon映射算法在分析暂态稳定评估输入特征有效性中的应用

张春, 田芳, 于之虹, 李岩松, 张爽, 田蓓

(1.华北电力大学电气与电子工程学院, 北京市 102206；2.中国电力科学研究院， 北京市 100192；3.国网宁夏电力公司电力科学研究院，银川市 750002)

改进Sammon映射算法在分析暂态稳定评估输入特征有效性中的应用

张春1, 田芳2, 于之虹2, 李岩松1, 张爽3, 田蓓3

(1.华北电力大学电气与电子工程学院, 北京市 102206；2.中国电力科学研究院， 北京市 100192；3.国网宁夏电力公司电力科学研究院，银川市 750002)

基于机器学习技术的电力系统暂态稳定评估方法中，输入特征提取的是否合理往往决定了最终的分类效果。然而，目前却缺乏一种工具去评价选择的输入特征是否具有可分性。鉴于此，引入Sammon映射算法将高维样本数据映射到低维空间中，通过观察映射点的分布情况判断提取的特征是否有效，并针对原算法的不足之处进行改进。首先利用主成分分析法(principal component analysis, PCA)求出包含原始数据信息最多的前两维主成分向量，代替原算法随机取值的方法，作为映射点坐标向量的初始值。然后，采用迭代修正法求解最终的映射点坐标向量，加快了求解速度。最后，以改进Sammon映射算法作为工具，分析IEEE 39节点系统的仿真数据和某地区实际在线历史数据提取特征的有效性，证明该算法在指导特征选择中具有良好的应用前景。

暂态稳定; 机器学习; Sammon映射; 特征有效性

0 引 言

随着我国特高压交直流电网的快速发展，给基于电力系统仿真方法的电力系统暂态稳定评估带来深刻变化和新的挑战[1]。近年来大数据处理、云计算等新一代IT技术在电力行业的广泛应用，日臻成熟的机器学习技术为电力系统暂态稳定评估带来了新的发展方向[2-3]。在应用机器学习技术的电力系统暂态稳定评估(transient stability assessment, TSA)方法中，为了减少冗余特征干扰，加快分类模型训练与预测的速度，特征提取是必不可少的步骤[4-5]。因此，最终的分类结果不仅与选择的分类方法有关，还与所选取的特征子集有关，因为输入特征的表达能力决定了输入空间的可分性。如果选取的输入特征是无效的，那么无论采用何种分类器都无法将稳定样本和失稳样本分开。由于缺乏一个有效的方法来评估提取特征的有效性，当采用某种方法进行分类时,如果分类结果不理想就无法判断问题究竟源于分类方法还是选择的输入特征不当。

为了解决这个无法判断问题来源的问题，本文引入可以分析数据结构特性的Sammon映射算法作为工具分析提取特征的有效性[6]。Sammon映射通过非线性变换可将一个高维的输入空间近似地转化为一个低维(二维)空间，且近似保持其数据内部的结构关系不变。因此，能够在低维空间上直接观察高维输入空间的可分性。目前，已有学者将其作为工具对电力系统中基于机器学习的分类问题进行研究。文献[7-8]利用Sammon映射分析基于神经网络的暂态稳定评估输入空间可分性。文献[9]根据Sammon映射分析暂稳评估稳定样本和失稳样本的边界问题。文献[10]利用Sammon映射将高维数据映射到低维以快速了解光伏电站功率数据的分布。然而，Sammon映射算法对初始值敏感，选取初值好坏往往会影响最终的映射结果。并且，传统Sammon映射算法采用随机数作为初值，以致映射结果不稳定，需要重复进行多次计算以选取稳定效果[11]。此外采用最速下降法求解低维空间映射点的坐标向量时迭代多、耗时长，在实际工程应用中受到很大限制[12]。

针对上述问题，本文提出一种改进Sammon算法。首先利用主成分分析法(principal component analysis, PCA)为Sammon映射提供有效的初始值。在此基础上，采用迭代修正方法求解映射点在低维空间中的坐标向量。最后，将改进算法应用于IEEE 39节点系统和实际某地区系统特征选取问题分析中。

1 主成分分析法的基本原理

PCA是多元统计学中常用的数据分析方法，其基本思想是利用原有变量线性组合出几个彼此不相关且尽可能保留原有变量信息的新变量，从而可以让较少不相关的新变量代替原有较多的相关联变量进行数据分析，所组合的新变量即为主成分[13]。根据统计学原理，一个变量的数据信息可以用其方差来表征，方差越大，所包含的信息量越大。

主成分分析是对多个样本的输入变量形成的数据矩阵求取相关矩阵，根据相关矩阵的特征值，获得累计方差贡献率，再根据相关矩阵的特征向量，确定主成分。具体步骤如下所示。

设由N个运行样本、p个特征构成的电力系统暂态稳定样本数据矩阵为

(1)

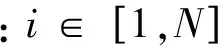
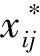
(2)

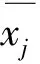
(2)建立标准矩阵X*的相关矩阵

(3)

并求出其特征值λ1≥λ2≥...≥λp及相应的特征向量u1,u2,...,up，X*为X标准化后的标准矩阵。

(3)确定主成分构成的矩阵。前m个主成分对应的特征向量为Up×m=[u1,u2,..,um]，则N个样本p个主成分构成的矩阵为

(4)

2 改进Sammon映射算法在分析特征有效性中的应用

2.1 算法思路分析

当采用某一算法提取子特征集后，Sammon映射算法将高维空间的样本点通过非线性变换映射到低维的二维空间中，然后观察稳定样本与失稳样本映射点类间边界区的重叠情况，进而分析所选特征的分类能力。稳定样本与失稳样本映射点重叠情况少说明该输入空间可分性好，选取特征能代表原始特征集的分类能力。重叠情况多则说明特征子集分类能力差，选取的特征是无效的，难以通过机器学习的方法对是否失稳进行分类。如果分类效果不理想，则需通过改进特征提取算法重新选择新的输入特征，最终选出有效的特征子集。Sammon映射算法指导分类特征选择的流程如图1所示。

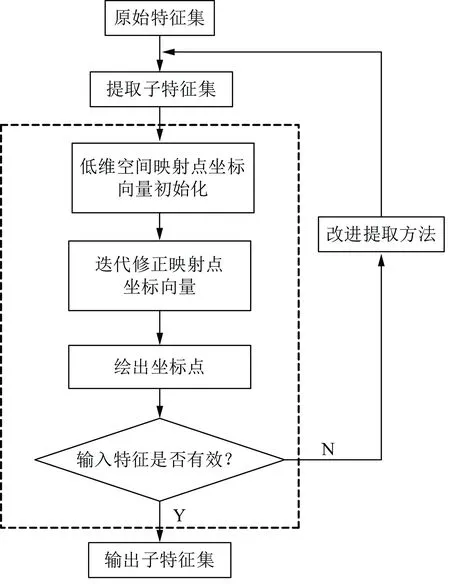
图1 算法流程图

在传统Sammon映射算法的映射过程中，2个重要因素影响着最终映射结果的稳定性和求解速度：低维空间映射点坐标向量初始值的选取和目标误差函数的最小化迭代过程[14]。后续的改进算法是针对传统Sammon算法的不足之处加以改进。

2.2 基于主成分分析的初值选取

Sammon映射算法对初始值的设定很敏感，初始值的设定会影响最终映射点的分布结果，所以当稳定样本与失稳样本映射点重叠较多时也有可能是由于初始值设置不当造成的，并非选取的特征无效。而传统Sammon映射算法是利用随机取值的随机数作为初始值的，所以有可能选取不当的初始值，导致对特征有效性分析的误判。因此，通常做法是进行多次计算，然后对比结果选出稳定的映射结果。这种求解方式的计算量大，重复很多不必要的计算。鉴于此，利用PCA法代替随机取值可以提供一个比较好的初始值[15]。用PCA求出原始样本中贡献率最大的两维主成分作为迭代的初始值，保留了原有矩阵的大部分信息，可以使映射结果更加稳定，减少不必要的计算。设低维空间映射点坐标向量的初始值为FN×2，则由式(4)得：

FN×2=X*[u1,u2]

(5)

式中u1、u2为相关矩阵R最大的2个特征值对应的特征向量。为了对比所述2种初值设定方法的映射效果，采用来自加州大学欧文分校的机器学习数据集中的葡萄酒数据对其分别进行测试[16]。

图2是采用随机选取初始值方法中的某一次的映射结果，图中各类样本重叠较多表明数据集特征是无效的，但实际特征集是有效的，表明这是由于初值不当而造成的误判。图3是采用PCA方法选取的初值，每次映射结果分布都一样，并能正确表示出特征集的分类能力，说明改进算法具有更好的稳定性。

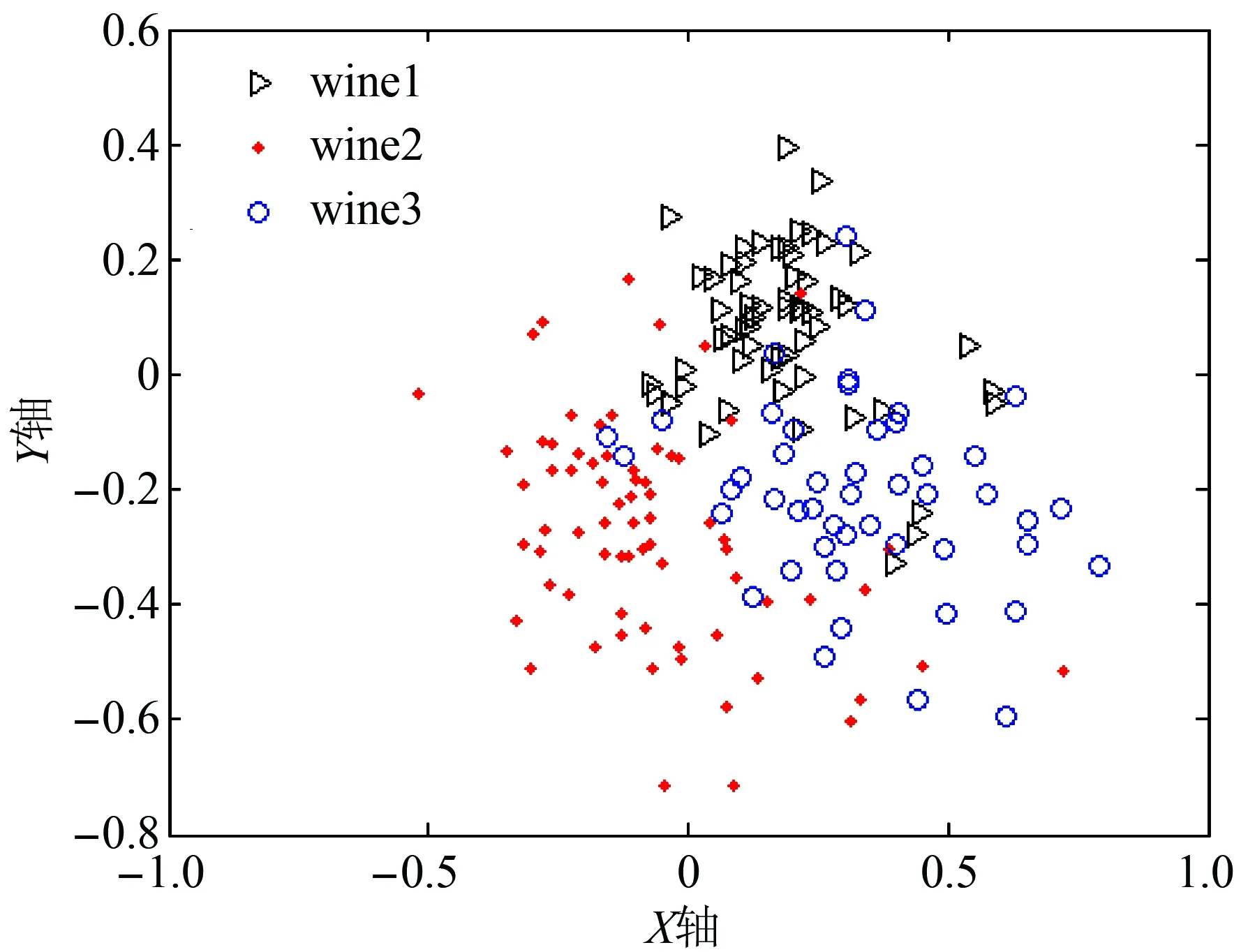
图2 采用随机取值法的映射结果

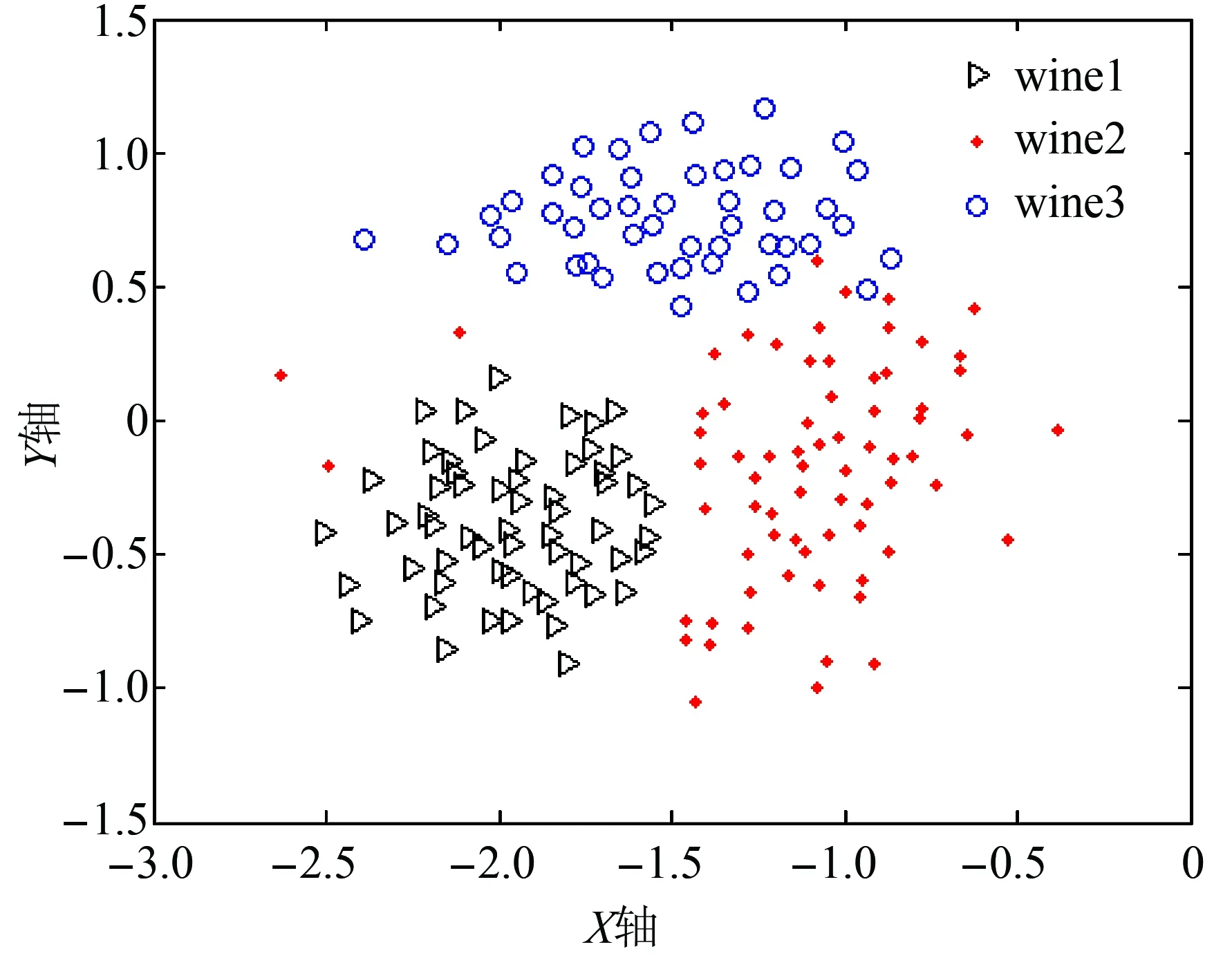
图3 采用PCA确定初值的映射结果

2.3 迭代修正过程

Sammon映射将样本点从高维空间“投影”到低维空间的非线性变换过程中，使低维空间中映射点相互之间的距离与高维空间中样本之间的距离尽量相同，从而保持各样本整体结构不变。因此，需要定义一个误差E代表从距离角度来讲，低维空间和高维空间样本点分布的相似程度[3]。

设在维度为p的高维空间中，有N个向量，p维空间中的数据样本向量Xi(i=1,...,N) 与样本向量Xj(j=1,...,N)之间的距离(欧式距离)表示为

(6)

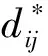
(7)

(8)

映射误差E代表了从距离角度来讲高维空间和低维空间的相似程度。映射误差越小，低维映射空间中数据结构关系与原始高维空间中的数据结构关系的相似程度越高，所以需要寻求N个能最小化目标函数E的低维空间坐标向量。当误差函数足够小时，低维映射点能够很好地保留原高维空间中的拓扑结构。

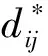
(9)

式中：Iteration为修正次数；maxIteration为总修正次数。迭代修正结束后通过式(7)、(8)计算映射误差E，当误差E小于某一设定阈值(本文设定的是10-6)时，停止迭代，输出映射点坐标。若不满足映射误差要求，则增加修正次数，继续迭代修正[17]。

改进Sammon算法利用迭代修正的方法调整低维空间映射点的坐标向量至目标误差函数值到一定范围内，比原最速下降法的求解速度更快。图4为利用不同数据规模的加州大学欧文分校的葡萄酒数据进行测试，可以看出当数据规模越来越大时，改进算法减少的时间更多。

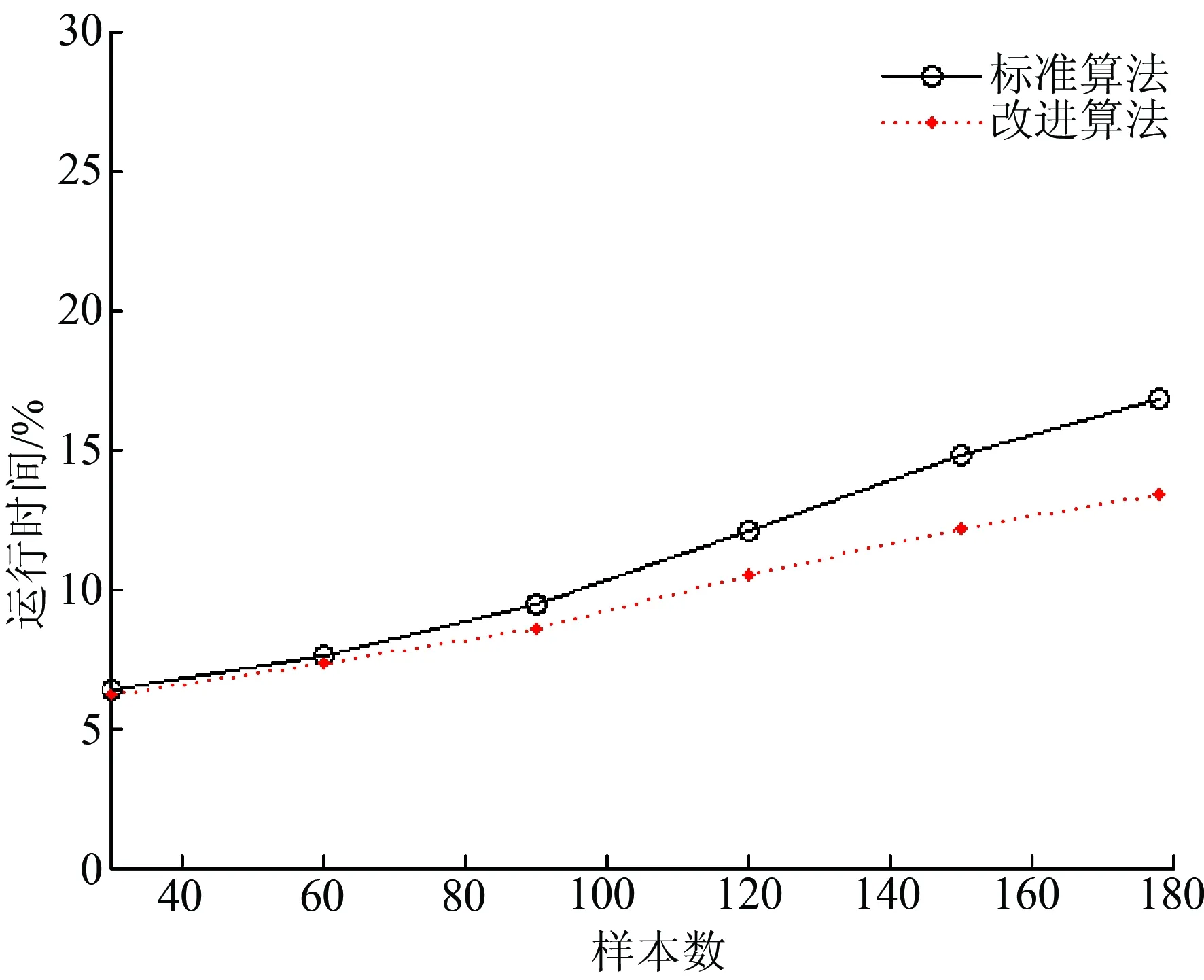
图4 映射样本个数与求解低维坐标时间

3 算例分析

3.1 测试系统与原始特征

3.1.1 IEEE 39节点系统

第1个算例采用经典的IEEE 39节点系统作为测试系统，系统结构如图5所示，包含10台发电机、39个节点、46条支路、19个负荷点。发电机模型采用4阶模型，负荷模型为恒阻抗模型[18]。

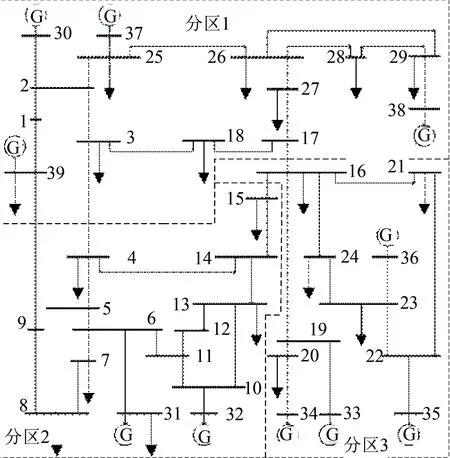
图5 IEEE 39节点系统

在电力系统运行过程中，随机电网潮流状态应满足潮流方程，而该方程为f(A,p,D,u,x)=0。其中A表示网络的结构变量；p表示输电线参数、变压器参数等的网络元件参数；D是不可控变量，例如一般意义上的系统负荷；u是控制变量，例如发电机的有功功率和机端电压、电容电抗器投切等；x是依从变量[19]。

上述4种变量确定后，系统的运行状态随之确定，这些被确定的量为依从变量。所以通过上述潮流方程发现，通过波动A，p，D，u均可以得到随即电网潮流方式，而本文中采用在不同负荷水平下波动控制变量中的发电机出力变量，来获取随机电网潮流状态：

(1)选择一个运行方式作为潮流基准，各负荷水平是以基准负荷85%～105%及以5%为步长得到5组负荷数据；

(2)发电机在线的有功出力，其波动范围是85%～115%，随机生成该范围内均匀随机数，每种负荷水平下随机生成400种潮流方案，共有2 000种随机潮流方式；

(3)每种潮流方案下，在母线3和4之间的线路中间设三相短路，1 s后切除线路和故障，用PSD-BPA软件进行时域仿真计算，在仿真结束时，以任意2台发电机的最大相对功角差是否大于360°来判定系统是否失稳[20-21]。

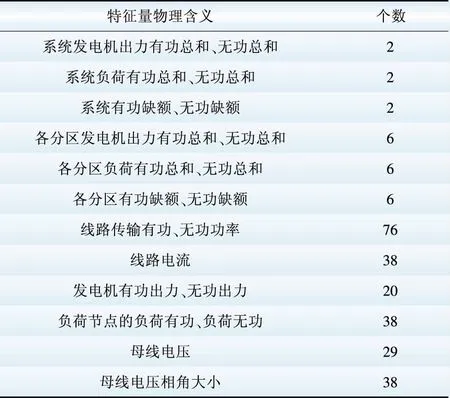
为客观评价各稳态状态变量对电网安全评估的贡献程度，选择的候选输入特征几乎涵盖了所有的电网稳态状态量。该测试系统共选取263维特征，如表1所示[22-23]。在2 000个仿真样本中，稳定样本有1 790个，失稳样本210个。

表1 IEEE 39节点系统原始特征集

Table 1 Original feature set of IEEE 39 bus system

3.1.2 某地区在线历史数据

第2个算例的测试数据采用某地区1个月的在线历史数据，故障考虑500 kV交流线路后备保护动作，根据计算出的极限切除时间是否超过0.3 s将系统分为稳定状态与失稳状态[24]。共选取有效在线数据1 979个，其中稳定样本1 910个，失稳样本69个。

至于在线数据，由于特征数过多，并且大多数特征与稳定程度相关性极小，所以首先利用相关性分析法，分析选取的输入特征与极限切除时间的相关性，进行初步筛选。其中，相关性分析是指分析2组变量数据之间的相关程度，常用的方法为相关系数计算，又称Person相关系数，计算公式如下：

(10)

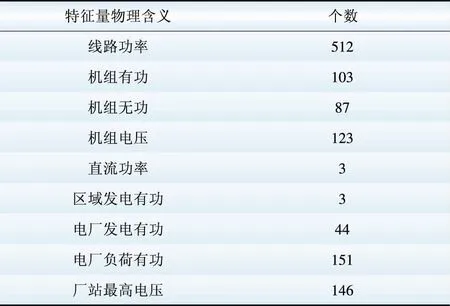
相关系数取值在-1到+1之间，大于0时代表2个序列正相关，即A值随B值的增加而增加，数值越接近于+1，则相关程度越强；反之小于0时代表2个序列负相关，越接近于-1，则相关程度越强；等于0时代表2个序列不相关。显而易见，应选取相关系数绝对值较大的电气量作为电网稳定特征。本文以0.3为阈值，选取绝对值大于或等于0.3的电气特征。利用相关性分析，进行初步筛选后，剩余1 173个稳定特征如表2所示。

表2 某地区系统原始特征集

Table 2 Original feature set of an area system

3.2 改进Sammon映射算法在指导特征选择中的应用

根据文献[25]中所提的，利用随机森林算法进行重要性排序计算，然后选取重要特征。随机森林是组合多棵决策树进行投票分类的集成学习算法，在训练分类模型的同时，也会计算各个特征的重要性得分。文献[25]根据随机森林计算出的重要性得分大小将特征排序，保留得分较大的特征，删除得分较小的特征。然而随机森林只能计算出特征得分大小，区分是否为重要特征的重要性得分阈值的大小通常是由人工决定。因此，需要根据本文提出的改进Sammon映射算法检验阈值选择的是否合理。图6是IEEE 39节点系统原始特征集映射到二维空间的样本点分布图，图7是选择重要性得分排名靠前的45个的特征作为输入特征得到的映射结果，图8选择的是前30个特征。同理，图9是某地区实际系统原始特征集映射后的分布情况，而图10是选择重要性得分排名靠前的113个特征作为输入特征映射后的结果，而图11只是选择前80个特征作为输入特征。

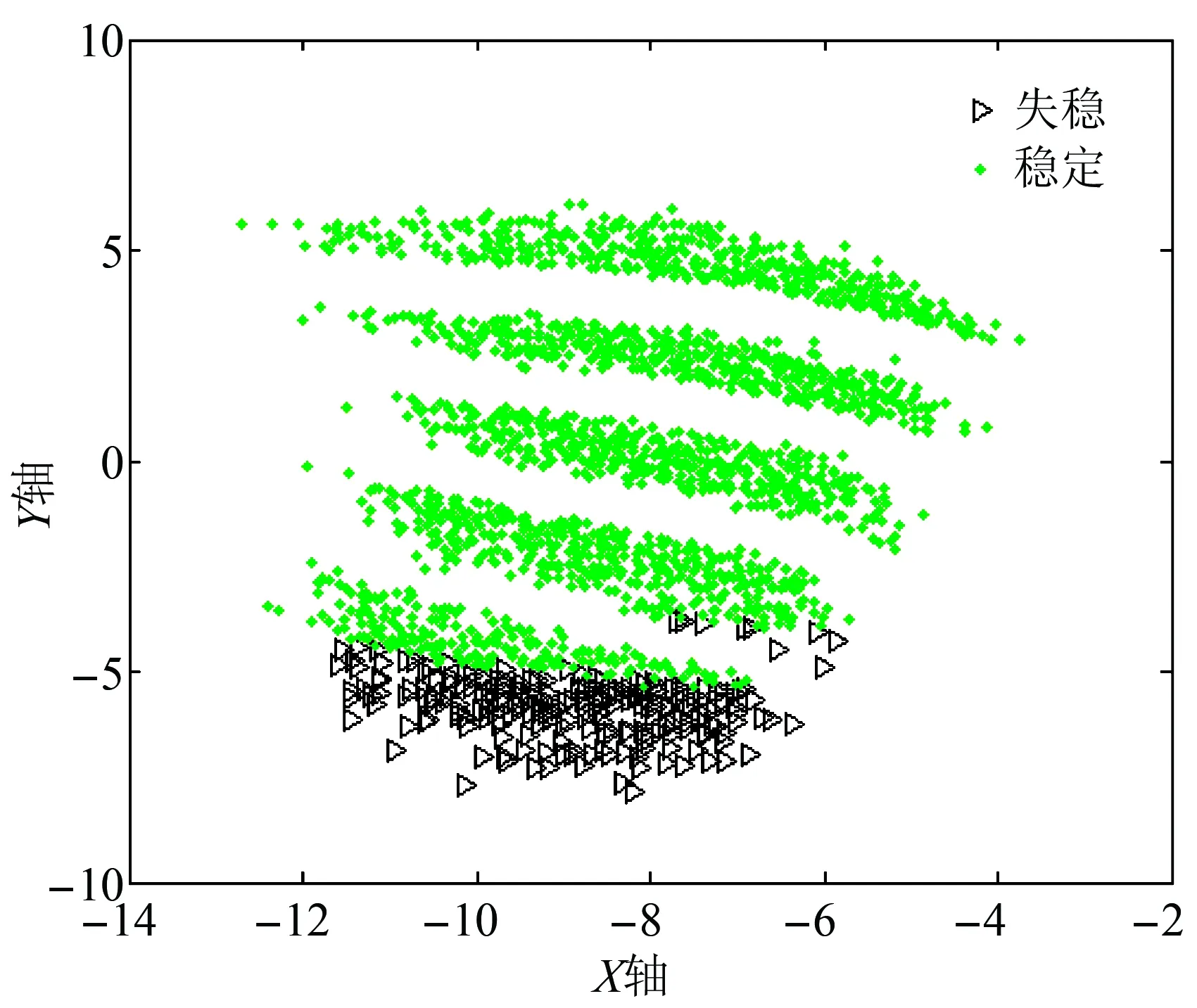
图6 IEEE 39系统原始特征集的映射结果

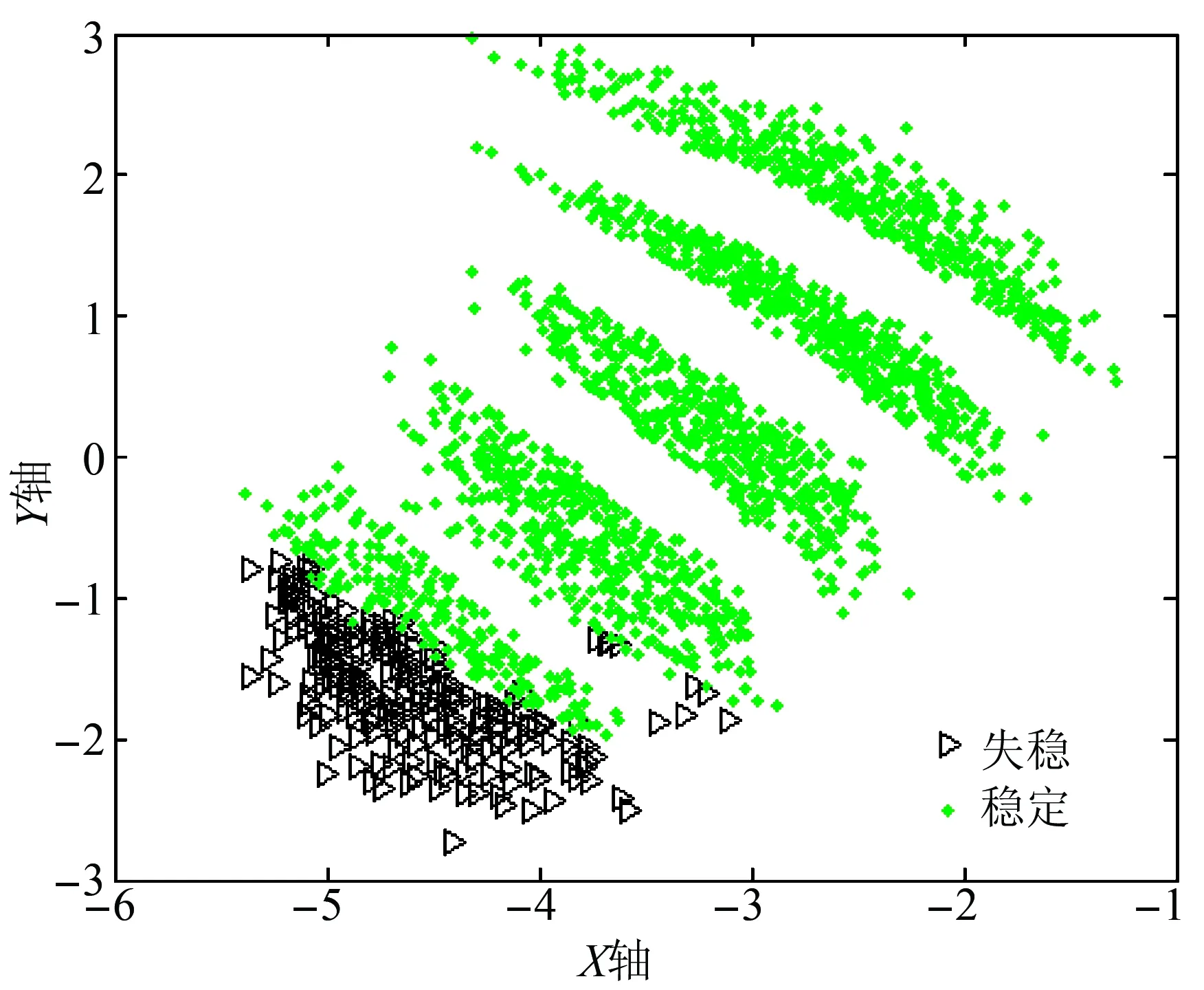
图7 IEEE 39系统提取前45个特征后的映射结果

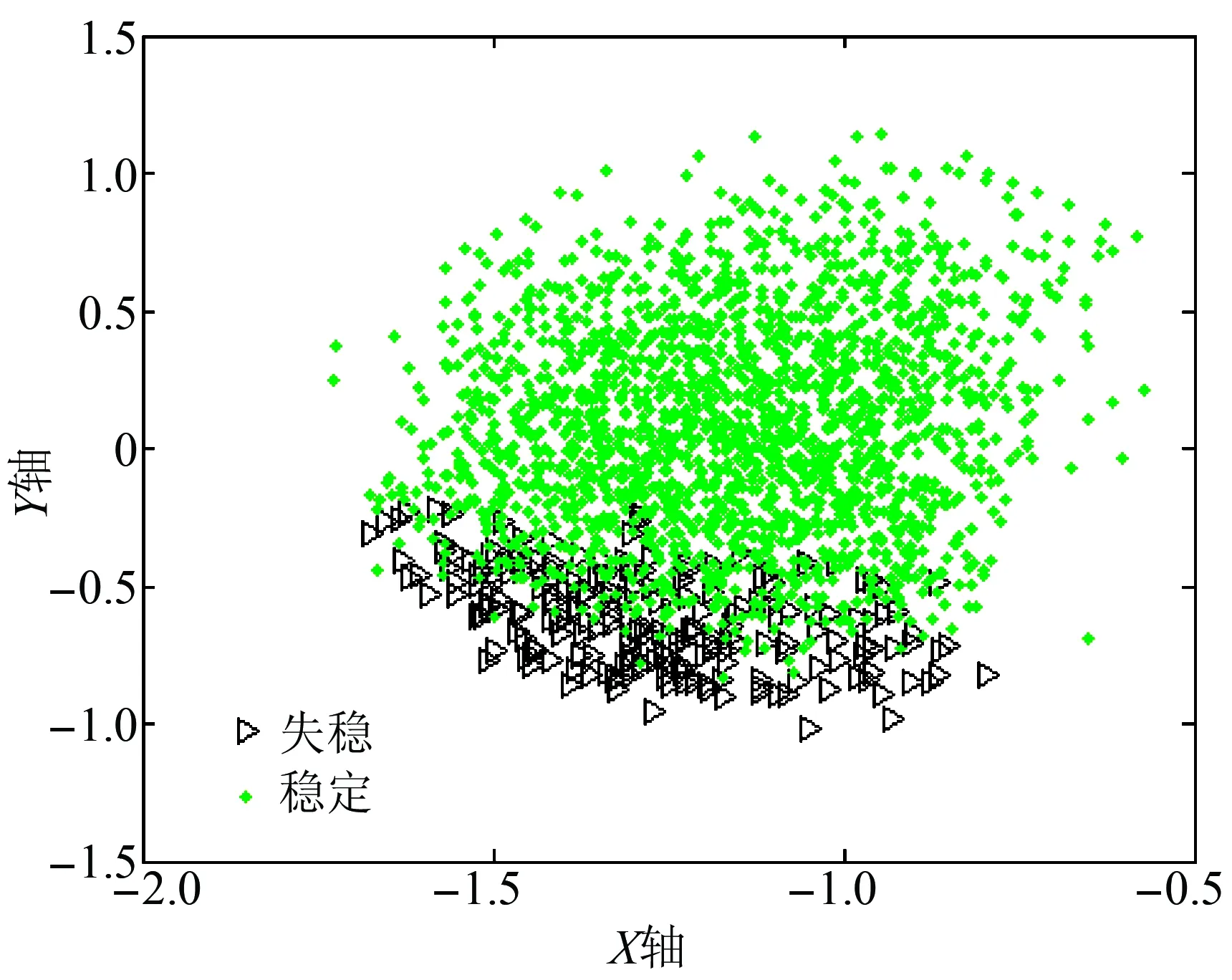
图8 IEEE 39系统提取前30个特征后的映射结果

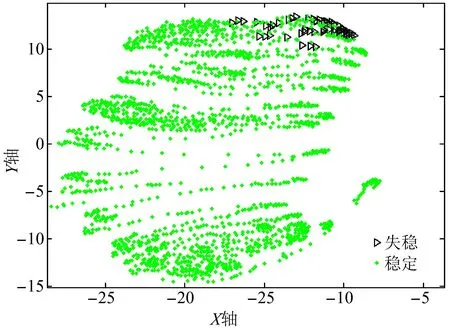
图9 某地区系统原始特征集的映射结果

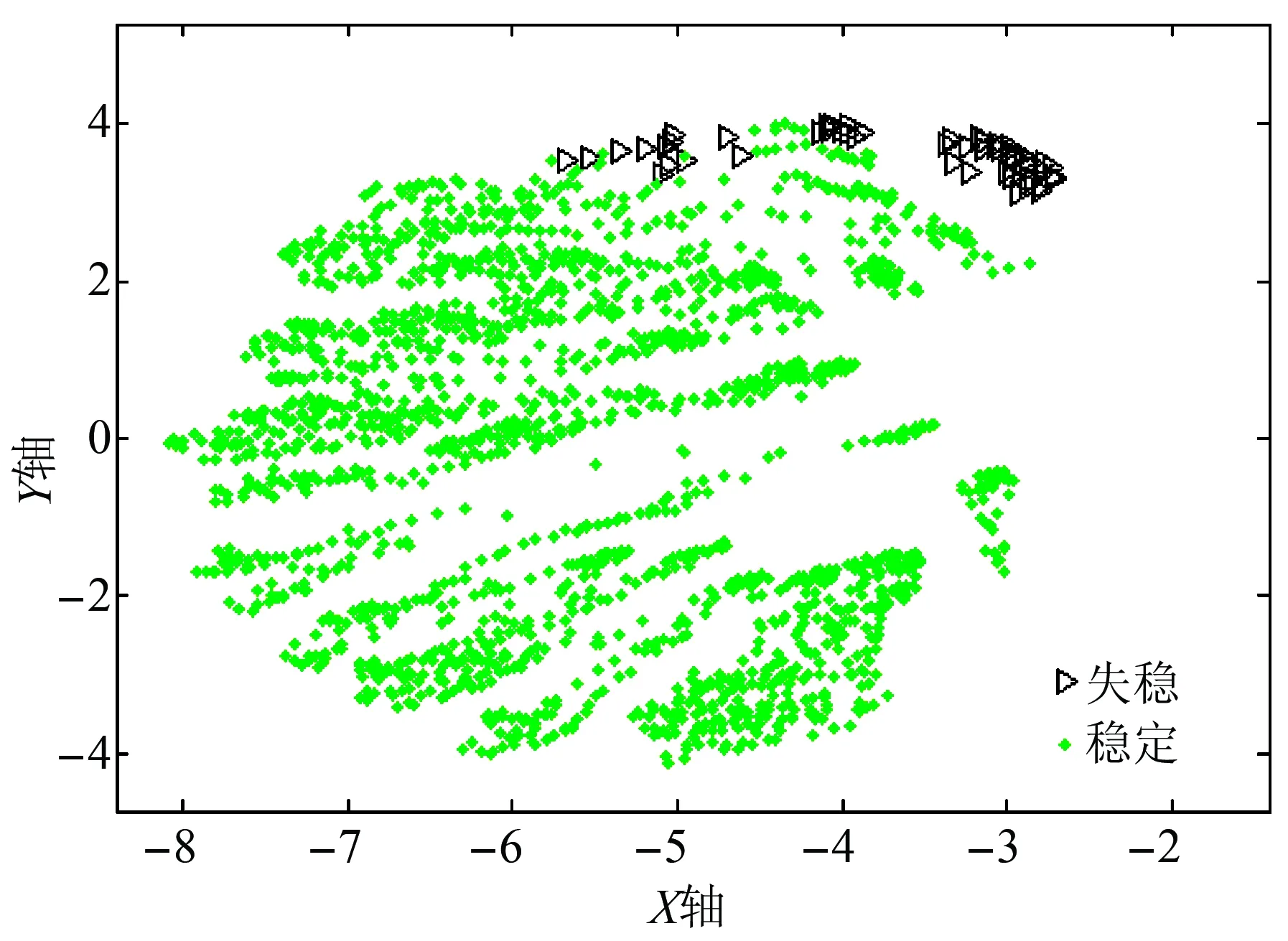
图10 某地区系统提取前113个特征后的映射结果

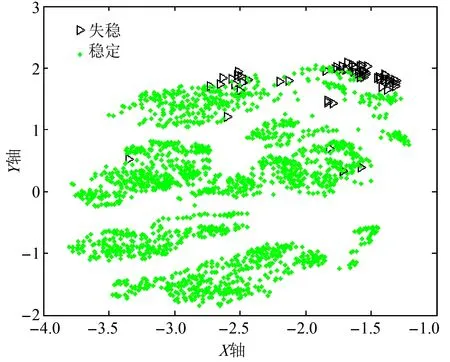
图11 某地区系统提取前80个特征后的映射结果

对比图6—8可知，提取重要性得分排名靠前45个特征子集作为输入特征后，映射结果和原始特征的映射结果基本保持不变，说明该子特征集仍保持原有的数据结构特性，选取的阈值是合理的。从只提取得分靠前的30个特征的映射分布图中可以看出，稳定样本和失稳样本映射点重叠较多，说明该子特征集不具有可分性，选取特征子集是无效的，需重新设定选取特征数的阈值大小。同理，对比图8—10可知，针对该地区的在线历史数据集，重要性得分阈值设定在选取前113个是合理的，而设定为80时，特征子集是无效的，会导致后续的分类效果不理想。

4 结 论

本文提出了一种基于主成分分析的改进Sammon映射算法，用于分析暂态稳定特征提取是否有效的问题，该算法具有以下特点。

(1)改进算法比原算法更具稳定性与高效性。一方面利用主成分分析法为迭代提供初始值，使映射结果稳定。另一方面，采用迭代修正的方法求解低维空间映射点坐标，加快了求解速度。

(2)该算法为分析输入空间的可分性提供了有力工具，对暂稳特征的选取具有很好的指导作用。同样，在其他基于机器学习的电力系统问题中也具有良好的应用前景。

[1]李亚楼, 张星, 李勇杰,等. 交直流混联大电网仿真技术现状及面临挑战[J]. 电力建设, 2015, 36(12):1-8.

LI Yalou, ZHANG Xing, LI Yongjie, et al. Present situation and challenges of AC/DC hybrid large-scale power grid simulation technology [J]. Electric Power Construction, 2015, 36(12):1-8.

[2]赵春晖, 姜大为, 崔灿,等. 大数据时代下的新型电网规划体系[J]. 电力建设, 2014, 35(10):17-20.

ZHAO Chunhui, JIANG Dawei, CUI Can, et al. New power grid planning system in big-data era[J]. Electric Power Construction,2014,35(10):17-20.

[3]张沛, 吴潇雨, 和敬涵. 大数据技术在主动配电网中的应用综述[J]. 电力建设, 2015, 36(1):52-59.

ZHANG Pei, WU Xiaoyu, HE Jinghan. Review on big data technology applied in active distribution network[J]. Electric Power Construction, 2015, 36(1):52-59.

[4]童晓阳，叶圣永．数据挖掘在电力系统暂态估中的应用综述[J]．电网技术，2009，33(20)：88-93．

TONG Xiaoyang，YE Shengyong．A survey on application of data mining in transient stability assessment of power system[J]．Power System Technology，2009，33(20)：88-93．

[5]王同文，管霖，张尧．人工智能技术在电网稳定评估中的应用综述[J]．电网技术，2009，33(12)：60-65．

WANG Tongwen，GUAN Lin，ZHANG Yao．A survey on application of artificial intelligence technology in power system stability assessment[J]．Power System Technology，2009，33(12)：60-65．

[6]SAMMON J W. A nonlinear mapping for data structure analysis[J]. IEEE Transactions on Computers, 1969, C-18(5): 401-409.

[7]顾雪平,张志刚,张文勤. 基于神经网络的暂态稳定评估输入空间可分性[J]. 华北电力大学学报,2000,27(2):16-20.

GU Xueping, ZHANG Zhigang , ZHANG Wenqin. Input space separability analysis of artificial neural networks based transient stability assessment[J].Journal of North China Electric Power University,2000,27(2):16-20.

[8]顾雪平,曹绍杰,张文勤. 基于神经网络暂态稳定评估方法的一种新思路[J]. 中国电机工程学报,2000,20(4):78-82.

GU Xueping, TSO Shiukit, ZHANG Wenqin. A new framework for transient stability assessment based on neural networks[J]. Proceedings of the CSEE, 2000, 20(4):77-82.

[9]YU Zhihong, ZHOU Xiaoxin, WU Zhongxi. Transient stability boundary visualization for power system[C]// International Conference on Power System Technology. IEEE, 2006.

[10]RADVANSKY M, KUDELKA M, SNASEL V. Identifying power profiles in the photovoltaic power station data by self-organizing maps and dimension reduction by Sammon’s projection[C]//Soft Computing and Pattern Recognition (SoCPaR).IEEE, 2013.

[11]陈敏. 智舌非线性模式识别方法研究[D].杭州：浙江工商大学,2012.

CHEN Min. The research of nonlinear pattern recognition methods for smartongue[D].Hangzhou: Zhejiang Gongshang University, 2012.

[12]周凌岚,叶浩欢,柳征,等. 基于改进Sammon映射的辐射源个体特征有效性分析[J].电子信息对抗技术,2010, 1(25):21-24.

ZHOU Linglan, YE Haohuan, LIU Zheng, et al. Validity analysis of emitter individual features based on an improved Sammon mapping [J].Electronic Warfare Technology, 2010, 1(25):21-24.

[13]崔巍，都秀文，杨海峰．基于主成分分析法的电力需求影响因素分析[J]．电力建设，2013，34( 8) : 34-39．

CUI Wei, DU Xiuwen, YANG Haifeng. Analysis on influencial factor of power demand based on principal component analysis[J]. Electric Power Construction,2013,34(8) : 34-39．

[14]LERNER B, GUTERMAN H, ALADJ E M, et al. Feature extraction by neural network nonlinear mapping for pattern classification[C]//13th International Conference on Pattern Recognition ( ICPR96). IEEE, 1996:320-324.

[15]KOVCS A, ABONYI J. Visualization of fuzzy clustering results by modified Sammon mapping[C]// IEEE International Conference on Fuzzy Systems. IEEE, 2004, 1(1):365-370.

[16]BACHE K, LICHMAN M. UCI Machine Learning Repository[EB/OL].[2016-06-05]. http//archive.ics.uci.edu/ml/datsets/wine.

[17]Kohonen T. Self-organizing Maps[ M]. 3rd Edition, Kerlin: Springer-Verlag, 2001.

[18]李扬，顾雪平．基于改进最大相关最小冗余判据的暂态稳定评估特征选择[J]．中国电机工程学报，2013，33(34)：179-186．

LI Yang，GU Xueping．Feature selection for transient stability assessment based on improved maximal relevance and minimal redundancy criterion [J]．Proceedings of the CSEE，2013，33(34)：179-186．

[19]张伯明，陈寿孙，严正. 高等电力网络分析[M]. 北京：清华大学出版社，2007.

[20]叶圣永，王晓茹，刘志刚，等．基于支持向量机的暂态稳定评估双阶段特征选择[J]．中国电机工程学报，2010，30(31)：28-34．

YE Shengyong，WANG Xiaoru，LIU Zhigang，et al． Dual-stage feature selection for transient stability assessment based on support vector machine [J]．Proceedings of the CSEE，2010，30(31)：28-34．

[21]GOMEZ F R，RAJAPAKSE A D，ANNAKKAGE U D，et al. Support vector machine-based algorithm for post-fault transient stability status prediction using synchronized measurements[J]. IEEE Transactions on Power System，2011,26(3):1474-1483.

[22]章小强. 智能稳定评估中的关键特征识别研究[D].广州：华南理工大学,2010.

ZHANG Xiaoqiang. Studies on kernel feature recognition for intelligent stability assessment [D]．Guangzhou: South China University of Technology，2010.

[23]于之虹，黄彦浩，鲁广明，等．基于时间序列关联分析的稳定运行规则提取方法[J]．中国电机工程学报，2015，35(3)：519-526．

YU Zhihong，HUANG Yanhao，LU Guangming，et al．A time series associative classification method for the operation rule extracting of transient stability[J]．Proceedings of the CSEE，2015，35(3)：519-526．

[24]国家电网公司． 国家电网安全稳定计算技术规范: Q/GDW 404—2010[S]. 北京： 国家电网公司，2010．

[25]黄彦浩，于之虹，史东宇，等. 基于海量在线历史数据的大电网快速判稳策略[J]. 中国电机工程学报，2016，36(3)：596-603.

HUANG Yanhao，YU Zhihong，SHI Dongyu，et al. Strategy of huge electric power system stability quick judgment based on massive historical online data [J]．Proceedings of the CSEE，2016，36(3)：596-603.

(编辑 刘文莹)

Application of Improved Sammon Mapping Algorithm in Input Features Validity Analysis of Transient Stability Assessment

ZHANG Chun1, TIAN Fang2, YU Zhihong2, LI Yansong1, ZHANG Shuang3, TIAN Bei3

(1. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China; 2. China Electric Power Research Institute, Beijing 100192, China; 3. Electric Power Research Institute, State Grid Ningxia Electric Power Company, Yinchuan 750002, China)

In the method of power system transient stability assessment based on machine learning technology, the reasonableness of the input feature extraction decides the final classification result. However, there were no tools to judge whether the selected input features are the separable. Therefore, this paper introduces the Sammon mapping algorithm to map high dimensional sample data to low dimensional space, determines the effectiveness of selected feature through observing the distribution of mapping points, and improves the original algorithm according to its deficiencies. Firstly, we adopted principal component analysis (PCA) method to obtain the first two dimensional principal component vectors containing the most original data information, which worked as the initial value of the mapping point coordinate vector instead of the random selection method in the original algorithm. Then, we used the iterative method to solve the coordinate vector of mapping points to accelerate the solving speed. Finally, we used the improved Sammon mapping algorithm as a tool to analyze the effectiveness of selected features of the numerical simulation data in IEEE39-bus system and the actual online historical data of a certain area. The analysis results show that the improved algorithm has a good application prospect in guiding feature selection.

transient stability; machine learning; Sammon mapping; feature effectiveness

国家重点基础研究发展计划项目(973项目)(2013CB228203);国家电网公司科技(XT71-15-001)

TM 71

A

1000-7229(2016)12-0096-08

10.3969/j.issn.1000-7229.2016.12.013

2016-07-07

张春(1991)，男，硕士研究生，主要研究方向为电力系统稳定与控制；

田芳(1973)，女，博士，教授级高工，主要研究方向为电力系统分析与控制，电力系统数字仿真等；

于之虹(1975)，女，工学博士，高级工程师，主要从事电力系统安全稳定评估与控制、仿真分析技术等方面的工作；

李岩松(1975)，男，博士，教授，研究方向为电力系统分析与控制、光学传感技术等;

张爽(1982)，男，高级工程师，主要从事电力系统计算、试验、科研方面的工作；

田蓓(1977)，女，高级工程师，从事电力系统计算与分析方面的工作。

Project supported by National Basic Research Program of China (973 Program) (2013CB228203)