基于双层功率分解的混合储能系统容量配置

王跃，吕林，朱雨薇

(四川省智能电网重点实验室(四川大学电气信息学院)，成都市610065)

基于双层功率分解的混合储能系统容量配置

王跃，吕林，朱雨薇

(四川省智能电网重点实验室(四川大学电气信息学院)，成都市610065)

为风电场配置合适的储能系统可以平抑风电有功功率波动、提高系统电能质量。基于风电出力历史数据，提出了双层功率分解方法。第1层采用滑动平均法，在满足国家规定的风电并网要求下，分解出并网功率和混合储能系统的参考功率。第2层采用频谱分析方法，基于混合储能系统参考功率，利用傅里叶变换将其分解为低频分量和高频分量，分别分配给蓄电池和超级电容器吸收。考虑储能设备的荷电状态和蓄电池的循环使用寿命，建立混合储能系统容量配置模型，模型以其年综合成本最小为优化目标。仿真结果验证了双层功率分解方法的可行性，证明了混合储能系统较单类型储能系统在性能上和经济上的优越性。

双层功率分解；滑动平均法；混合储能；频谱分析；循环使用寿命；年综合成本

0 引 言

风电出力的随机性和波动性严重制约了风电并网的规模[1]。由于储能能够实现电能的时空平移，被认为是平抑风电出力波动、提高电网风电接纳能力的最有效手段[2-4]。

单类型储能很难同时满足功率和能量这2个方面的需求[5-6]，所以采用混合储能平抑风电出力波动已成为微电网技术研究的热点。文献[7]考虑电池的使用寿命，搭建系统容量配置模型，分析了混合储能系统成本结构。文献[8]考虑了储能因平抑风电功率波动产生的效益，建立了以系统净效益最大为目标的容量配置模型。文献[9]针对孤岛型微电网，考虑了系统缺电损失费用和弃风惩罚费用，建立了混合储能容量配置模型。文献[10]分析了不同储能系统对风力发电输出功率的补偿特性，提出了基于混合储能系统平抑风电波动的控制策略。上述文献分别从经济角度和性能角度验证了混合储能比单类型储能系统具有巨大优势。

目前，混合储能系统的研究主要集中于控制策略上，在容量优化配置方面缺乏深入研究。文献[11-14]在低通滤波方法的基础上，建立混合储能系统容量优化模型。然而，低通滤波器在滤波的过程中会产生一定的延迟，这将造成储能系统配置容量偏高，导致成本增大。文献[15]基于小波分解方法分解混合储能系统参考功率，给出了混合储能系统容量配置模型。但是，小波分解方法会因为基波的选择不同而使分解出来的信号分量产生变化，导致重构过程产生误差。文献[16]利用经验模态分解方法，采用神经网络模型优化混合储能系统的容量，通过成本和平滑度指标之间的折中实现混合储能的容量优化配置。

本文基于风电出力历史数据，提出双层功率分解方法。第1层采用滑动平均法分解出满足并网要求的并网功率。第2层利用傅里叶变换将混合储能系统参考功率分解为低频分量和高频分量分别分配给蓄电池和超级电容器。考虑储能设备的荷电状态和蓄电池的循环使用寿命，建立混合储能系统容量优化模型，模型以其年综合成本最小为优化目标，以充放电功率、剩余电量等为约束条件。最后，以我国西北地区某风储联合发电系统为例，验证双层功率分解方法的可行性和混合储能系统的优越性。

1 风储联合发电系统模型

1.1 风储联合发电系统结构

图1为风储联合发电系统结构，该系统由风力发电系统和混合储能系统组成。储能系统用来平抑风电输出功率的波动，以满足并网要求。混合储能系统包含蓄电池和超级电容器。蓄电池作为能量型储能设备，其能量密度大，适合处理能量高的低频功率波动。超级电容器作为功率型储能设备，其功率密度大，响应时间短，可频繁充放电，适合处理能量低的高频功率波动。通过储能逆变器，蓄电池和超级电容器与母线连接起来。控制中心通过对风力发电系统和混合储能系统的控制，使风储联合发电系统输出的功率达到国家规定的并网要求，同时控制混合储能系统中蓄电池和超级电容器的充放电状态，使储能系统工作于最优状态。

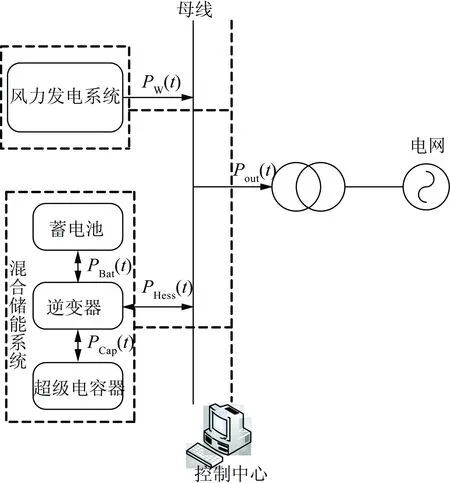
图1 风储联合发电系统结构

图中，Pw(t)为t时刻风力发电系统输出功率；PHess(t)为t时刻混合储能系统的输出功率，为正则表示储能系统放电，为负则表示储能系统充电；PBat(t)为t时刻蓄电池充放电功率；PCap(t)为t时刻超级电容器充放电功率；Pout(t)为t时刻风储联合发电系统并网功率。

Pout(t)=Pw(t)+PHess(t)=Pw(t)+

PBat(t)+PCap(t)

(1)

1.2 储能系统充放电模型

储能设备的剩余电量与该设备的充放电功率和初始荷电量有关。当风储联合发电系统输出功率大于并网功率时，需要储能系统吸收多余的有功功率，储能设备充电，其充电模型为

(2)

式中：EBat(t)、ECap(t)分别为蓄电池和超级电容器t时刻的剩余电量；PBat(t)、PCap(t)分别为蓄电池和超级电容器t时刻实际充电功率；ηBc、ηCc分别为蓄电池和超级电容器充电效率；Δt为时间步长。

当风储联合发电系统输出功率小于并网功率时，需要储能系统补偿缺失的有功功率，储能设备放电，其放电模型为

(3)

式中ηBd、ηCd分别为蓄电池和超级电容器的放电效率。

1.3 蓄电池经济寿命模型

超级电容器循环使用寿命很长，计算经济寿命时一般将其设定为固定值，本文设为20年。蓄电池的循环使用寿命主要与放电深度和充放电次数有关。本文在文献[17]的基础上，搭建蓄电池经济寿命模型。

蓄电池在工作过程中，放电深度越大，其循环使用次数越少。两者之间的函数关系为

(4)

式中：Dr、Dj分别为额定放电深度与第j次实际放电深度；Nr、Nj分别为对应于额定放电深度和第j次实际放电深度的循环使用次数；α1、α2为函数关系式的拟合系数。

则蓄电池第j次放电的等效循环使用次数为

(5)

1年内，蓄电池不同放电过程折算到额定放电深度下的有效放电电量为

(6)

式中：Eeffect为1年内不同放电深度折算到额定放电深度下的有效放电电量， MW·h/a；Ni为电池储能系统在1年内第i天经历的放电过程数；Pj、Δt分别为该放电过程的放电功率和经历的时间；Kj为其对应的等效循环使用次数。

额定放电深度下，电池使用寿命内其放电电量为

Er=NrDrEBat

(7)

式中：Er为额定放电深度下电池储能系统在其使用寿命内的放电电量， MW·h；EBat为电池储能系统的额定容量。

因此，蓄电池的使用寿命为

(8)

式中YBat为电池储能的使用寿命，a。

2 双层功率分解

本文基于风力发电历史数据进行双层功率分解，其分解过程如图2所示。风电出力波动较大，不适合直接并网，经过滑动平均法(为了避免产生延迟，采用前向数据和后向数据的中点平均)分解为满足并网要求的并网功率Pout(t)和混合储能系统的参考功率Pref(t)。混合储能系统参考功率经过傅里叶变换，选择低频部分进行傅里叶反变换得到低频分量作为蓄电池的参考功率，高频分量作为超级电容器的参考功率。

图2 双层功率分解方法

2.1 并网功率分解

本文选择滑动平均法分解风电功率，以满足并网要求。滑动平均法是将动态测试数据在一定范围内进行算术平均的数学方法[12]。

Pw(i)=Pout(i)+Pref(i),i=1,2,...,N

(9)

式中：Pw(i)为风电输出功率波动数据；Pout(i)为所需的输出结果，即并网功率；Pref(i)为随机起伏的数据误差，即混合储能系统的参考功率；N为采样点数。

对非平稳的风电功率Pw在适当的小区间上视为接近平稳的。将N个数据分别在窗口大小为s的小范围内进行局部平均，就得到较平滑的并网功率Pout。

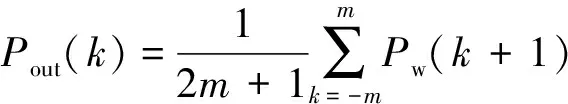
k=m+1,m+2,...,N-m

(10)

式中2m+1=s。

2.2 蓄电池和超级电容器功率分解

以滑动平均法分解出的并网功率和风电出力历史监测数据为基础，利用频谱分析方法，确定蓄电池和超级电容器的平抑目标，实现对风电出力波动量的平抑。t时刻风电出力为Pw(t),并网功率为Pout(t),则该时刻混合储能系统需平抑的目标值为

Pref(t)=Pw(t)-Pout(t)

(11)

若Pref(t)>0，则需要储能系统吸收过剩的风电出力，储能系统处于充电状态；若Pref(t)<0，则需要储能系统补偿风电出力，储能系统处于放电状态。

信号Pref(t)可以看作一个采样点数为N的时域离散信号，设采样周期为Ts，采样频率为fs，则Pref(t)可以视为1个周期为NTs的信号，该信号基频为1/(NTs)，通过傅里叶变换可将不平衡功率变换成直流分量、基频周期分量以及倍频周期分量之和的形式。

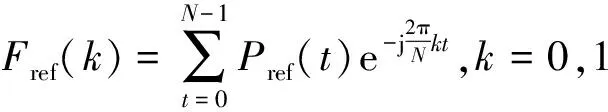
(12)

式中k为频率的序列数，k=0表示直流分量，k=1表示基频分量，k=2表示2倍基频分量，依次类推。

令WN=e-j2π/N，将式(12)展开，可得到第k项展开式如下：

(13)

为体现直流分量Fref(0)的对称性，Fref(k)可表示为

(14)

将上式在k=n处切断，相当于同时也在对称位置k=N-n处切断为2个部分，将这个n称为“分断点”，取值范围为[0,N/2](N/2为对称轴)。将被截断的2个部分列出，并各自将缺失的部分补0，可得

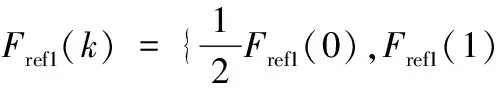
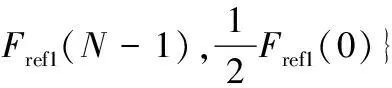
(15)

Fref2(k)={0,...,0,Fref2(n+1),Fref2(n+2),...,

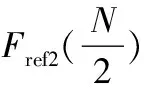
(16)

式中：Fref1(k)为低频部分；Fref2(k)为高频部分。

将低频部分和高频部分进行傅里叶逆变换:

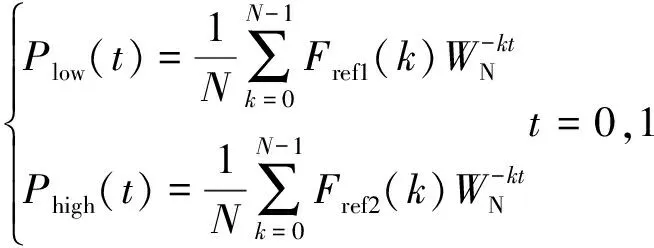
(17)

式中：Plow(t)为低频分量；Phigh(t)为高频分量。

3 混合储能系统容量配置

3.1 目标函数

本文以混合储能系统年综合成本最小为优化目标，进行蓄电池和超级电容器的容量配置。其年综合成本包括年等效投资成本和年运行维护成本。

年等效投资成本：

(18)

式中：Cinv为年等效投资成本；αpinv为单位功率投资成本；αeinv为单位容量投资成本；Prate、Erate分别为额定功率和额定容量；Ny为储能设备的运行年限。

年运行维护成本：

Cmain=βmainErate

(19)

式中：Cmain为年运行维护成本；βmain为单位容量的运行维护成本。

综上所述，年综合最小成本为

(20)

3.2 约束条件

为更好地配置混合储能系统容量，需要考虑以下3个方面的约束条件。

(1)能量守恒约束。风电出力、蓄电池出力和超级电容器出力之和应当与并网功率相一致，系统功率平衡应当满足：

Pw(t)+PBat(t)+PCap(t)=Pout(t)

(21)

(2)储能系统容量约束。任意时刻储能设备中剩余电量都应该在合理的范围内，设备过充和过放都会影响其使用寿命，因此蓄电池和超级电容器的剩余电量在任何时刻都不能超过其上、下限:

(22)

式中EBatmax、EBatmin、ECapmax、ECapmin分别为蓄电池和超级电容器剩余电量的上下限。

(3)储能系统功率约束。蓄电池和超级电容器的充放电功率不能超过其额定功率：

(23)

式中：PBatc(t)、PBatd(t)分别为蓄电池在t时刻的充放电功率；PCapc(t)、PCapd(t)分别为超级电容器在t时刻的充放电功率；PBat、PCap分别蓄电池和超级电容器的额定功率。

3.3 优化算法

本文所研究的混合储能系统容量优化配置模型是一个非线性、多变量的数学模型，采用粒子群算法进行求解。以蓄电池和超级电容器额定功率和额定容量为变量进行寻优，具体优化过程见文献[7]。

4 算例分析

为验证双层功率分解方法的可行性和混合储能系统平抑风电波动的优越性，本文采用某22 MW风电场2013年典型日的输出功率数据进行仿真分析。采样时间间隔为1 min，最大输出功率为18.9 MW,最小输出功率为4.2 MW。储能设备初始电量为额定容量的50%。系统相关参数见表1。

根据我国风电并网标准：风电装机容量小于30 MW时，任意1 min有功功率变化不大于3 MW，任意10 min有功功率变化不大于10 MW，通过滑动平均法得到满足波动率约束下的最小滑动时窗为57个。

表1 系统相关参数

Table 1 System related parameters

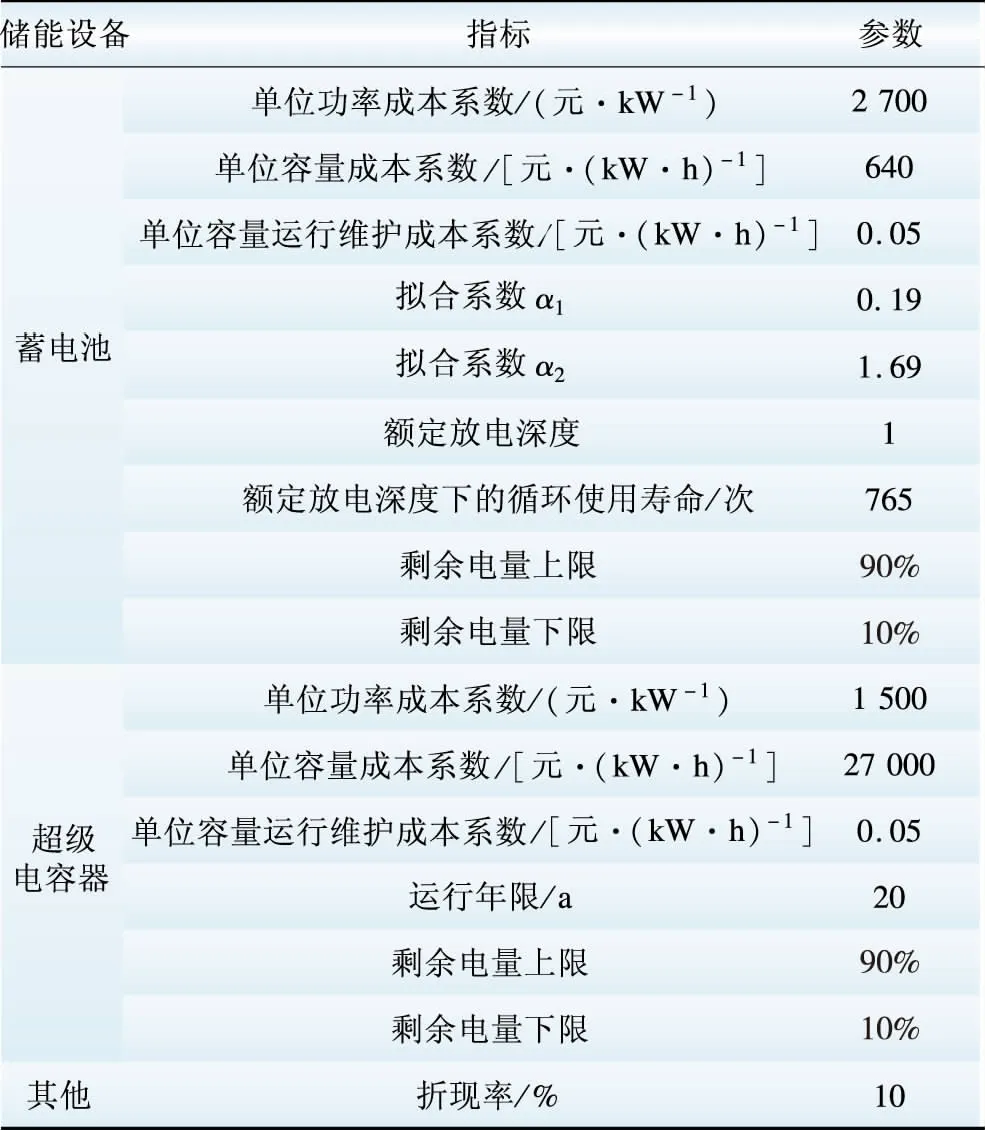
图3为某典型日风电出力历史数据和采用滑动平均法处理且满足并网要求的并网功率曲线。由图3可知，风电出力具有很大的随机性和波动性，这严重限制了大规模风电功率并网。滑动平均法在满足并网要求的情况下，将风电功率曲线进行平滑处理，以便于风电并网。

滑动平均前后风力发电数据统计情况见表2。比较滑动平均前后风电数据，可知，平滑后的并网功率各项波动指标均显著下降。1 min最大波动率下降6.053%，10 min最大波动功率下降13.218%。其 1 min和10 min最大功率波动量和波动率均满足并网标准。

表2 风电数据统计情况

Table 2 Statistics of wind data

采用本文方法获得混合储能系统参考功率后，对参考功率运用离散傅里叶变换进行频谱分析，如图4所示。根据傅里叶变换频域的对称性可知，只需对前半部分进行分析即可。可以看出，储能系统参考功率波动成分主要集中在n=0～200，低频波动的幅值较大，高频波动的幅值越来越小，且越来越缓慢。

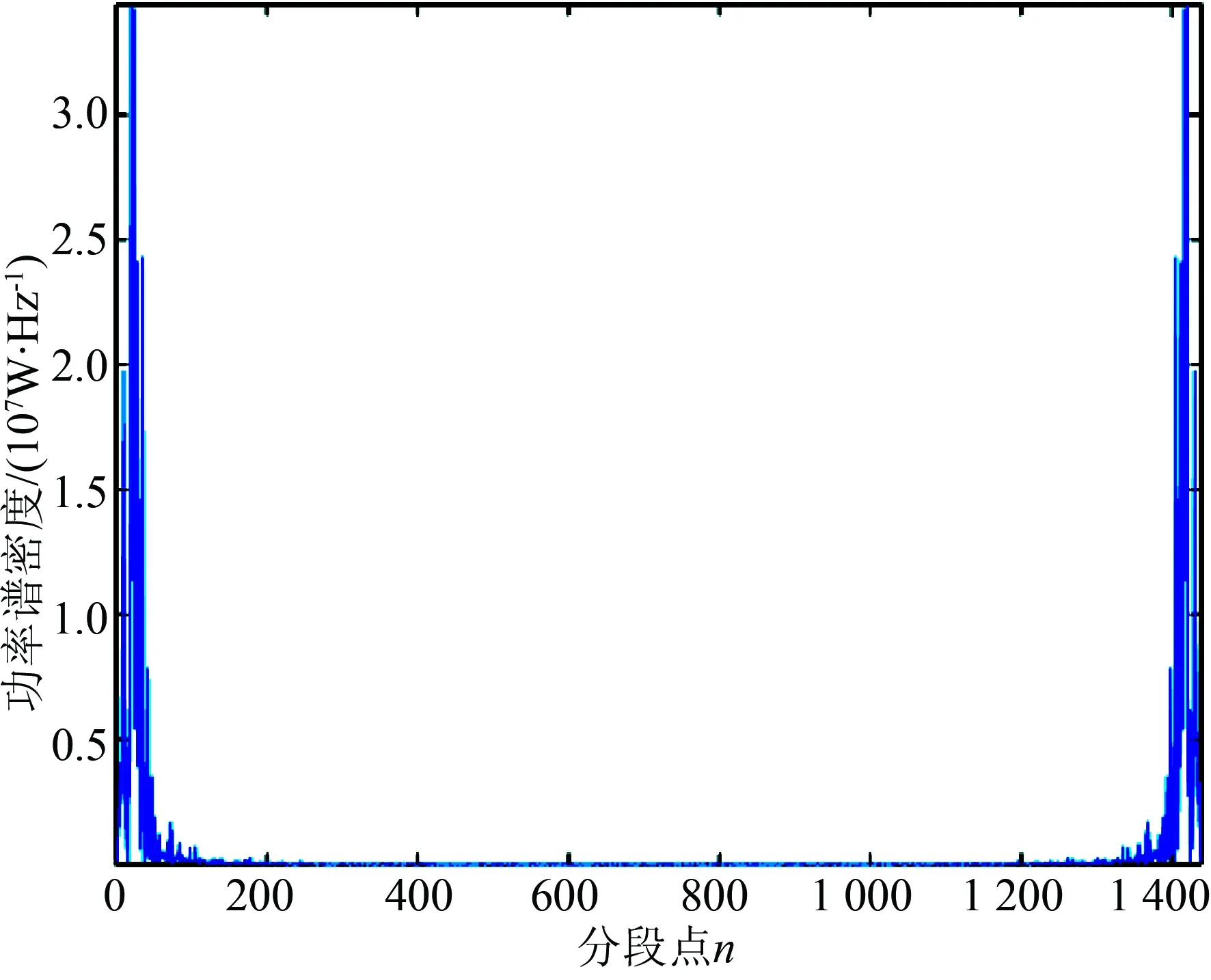
图4 储能系统参考功率频谱分析

分断点的选择，直接关系到蓄电池和超级电容器储能系统容量配置的大小，进而影响混合储能系统年综合成本的大小。不同分断点下的混合储能系统年综合成本如图5所示。

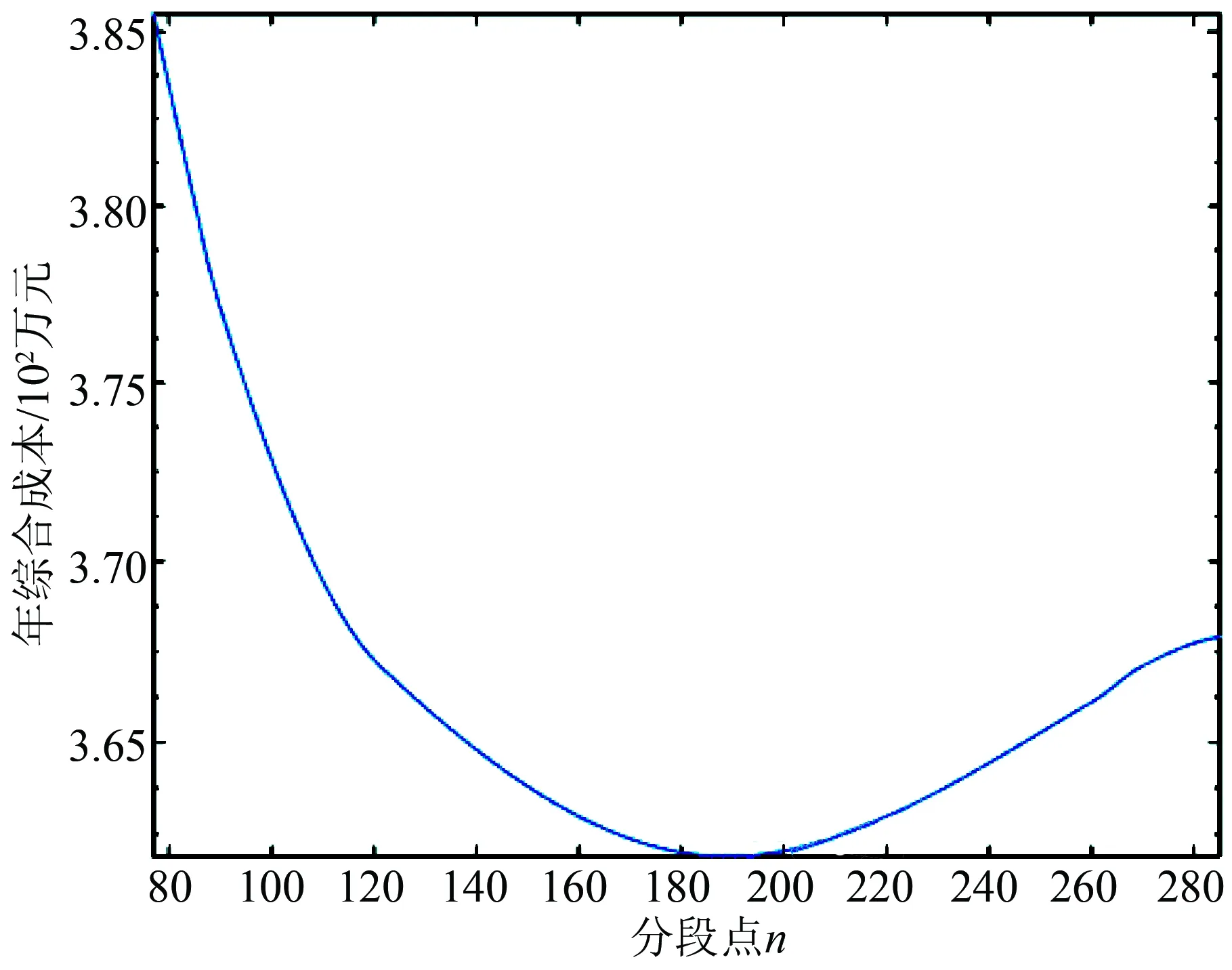
图5 分断点与成本的关系

由图5可知，储能系统年综合成本随分断点的增大呈先减小后增大趋势。这主要是因为，随着分断点的增大，蓄电池的配置容量逐渐增大的同时超级电容器的配置容量迅速减小，使得储能系统年综合成本降低。分断点继续增大，蓄电池的运行寿命迅速减小，超级电容器的配置容量变化不大，储能系统年综合成本呈上升趋势。图6为分断点与蓄电池运行寿命的关系。

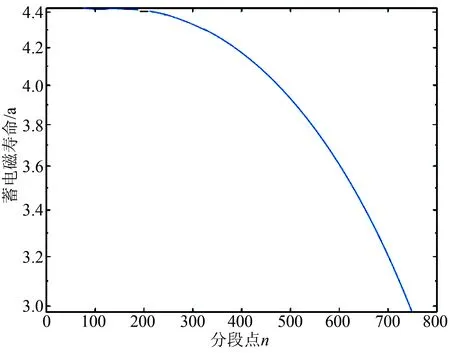
图6 分断点与运行寿命的关系

取n=189时，蓄电池和超级电容器功率分配曲线如图7所示。由图7可知，蓄电池主要平抑储能参考功率中的长时间、大幅度的功率波动分量，而超级电容器可有效地平抑短时间、小幅度的功率波动分量。

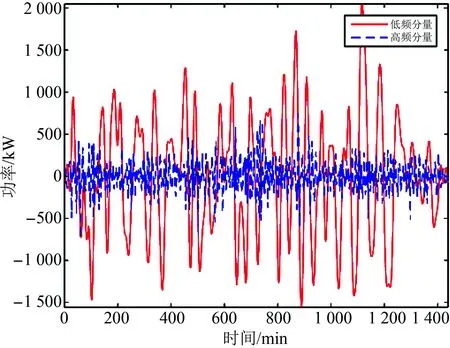
图7 功率分配曲线

基于储能设备的充放电模型和可变寿命模型，利用系统风力发电出力数据，采用粒子群算法优化混合储能系统容量。取迭代次数为100次，种群规模为100个，混合储能系统容量优化配置结果如表3所示。其中，方案1为蓄电池单类型储能；方案2为超级电容器单类型储能；方案3采用本文频谱分析方法，储能设备选用蓄电池和超级电容器；方案4采用低通滤波分析方法，储能设备选用蓄电池和超级电容器。

表3 容量配置结果

Table 3 Results of capacity allocation

由表3可知，方案1和方案2相比，方案1中采用单一蓄电池储能，其年综合成本降低了40.8%。这是因为蓄电池为能量型储能设备，其容量成本远低于超级电容器的容量成本，尽管蓄电池的容量配置远大于超级电容器的容量配置，但其年综合成本仍低于超级电容器的年综合成本。方案1和方案3相比，方案3中混合储能系统的年综合成本低于单一蓄电池系统。这是因为采用混合储能系统平抑风力发电出力波动，虽然蓄电池的容量配置变化不大，但是由于超级电容器作为功率型储能系统，其功率密度大，响应时间短，可频繁充放电，大幅延长了蓄电池的运行年限，使得因蓄电池寿命延长而减小的成本大于因超级电容器配置的成本。方案3和方案4相比，方案4中蓄电池配置的容量大于方案3，且方案4的年综合成本也高于方案3。这主要是低通滤波器在滤波的过程中会产生一定的延迟，这将导致储能系统优化容量偏高，蓄电池运行寿命降低，其年综合成本增大。

5 结 论

为满足国家风电并网要求，利用滑动平均法能有效分解得到平滑的并网功率曲线；为分配蓄电池和超级电容器的平抑目标，采用频谱分析法能得到合适的低频分量和高频分量；为优化储能系统年综合成本，分析了不同分断点与成本之间的关系，从而找到经济最优的分断点。

考虑储能设备的荷电状态和蓄电池的循环使用寿命，建立了混合储能系统容量优化模型。通过分析不同配置方案下储能系统年综合成本大小，验证了双层功率分解方法的可行性和经济性，证明了混合储能系统较单类型储能在性能上和经济上的优越性。

[1]孟虹年，谢开贵．计及电池储能设备运行特性的风电场可靠性评估[J]．电网技术，2012，36(6)：214-219．

MENG Hongnian，XIE Kaigui．Wind farm reliability evaluation considering operation characteristics of battery energy storage devices[J]．Power System Technology，2012，36(6)：214-219．

[2]严干贵，朱星旭，李军徽，等．内蕴运行寿命测算的混合储能系统控制策略设计[J] ．电力系统自动化，2013，37(1):110-114．

YAN Gangui，ZHU Xingxu，LI Junhui，et al．Control strategy design for hybrid energy storage system with intrinsic operation life measurement and calculation[J]．Automation of Electric Power Systems，2013，37(1):110-114．

[3]肖峻，张泽群，张磐，等．用于优化微网联络线功率的混合储能容量优化方法[J] ．电力系统自动化，2014，38(12):19-26．

XIAO Jun，ZHANG Zequn，ZHANG Pan，et al．A capacity optimization method of hybrid energy system for optimizing tie-line power in micro-grids[J] ．Automation of Electric Power Systems，2014，38(12):19-26．

[4]黄秀琼，丁若星，肖曦，等．混合储能系统中超级电容器的作用及容量设计方法[J] ．电力建设，2014，35(12):67-71．

HUANG Xiuqiong，DING Ruoxing，XIAO Xi，et al．Role and capacity design method of super-capacitor in hybrid energy storage system[J] ．Electric Power Construction，2014，35(12):67-71．

[5]程启明，徐聪，程尹曼，等．基于混合储能技术的光储式充电站直流微网系统协调控制[J] ．高电压技术，2016，42(7):2073-2083．

CHENG Qiming，XU Chong，CENG Yinman，et al．Coordination control of PV charging station DC microgrid system based on hybrid energy storage technology[J] ．High Voltage Engineering，2016，42(7):2073-2083．

[6]王宁，张建成．基于能量协调控制的混合储能系统容量配置方法[J] ．电力建设，2016，37(8):72-77．

WANG Ning，ZHANG Jiancheng．Capacity allocation method of hybrid energy storage system based on energy coordination control[J] ．Electric Power Construction，2016，37(8):72-77．

[7]韩晓娟，程成，籍天明，等．计及电池使用寿命的混合储能系统容量优化模型[J] ．中国电机工程学报，2013，33(34):91-97．

HAN Xiaojuan，CHENG Cheng，JI Tianming，et al．Capacity optimal modeling of hybrid energy storage systems considering battery life[J] ．Proceedings of the CSEE，2013，33(34):91-97．

[8]张晴，李欣然，杨明，等．净效益最大的平抑风电功能波动的混合储能容量配置方法[J] ．电工技术学报，2016，31(14):40-48．

ZHANG Qing，LI Xinran，YANG Ming，et al．Capacity determination of hybrid energy storage system for smoothing wind power fluctuations with maximum net benefit[J] ．Transactions of China Electrotechnical Society，2016，31(14):40-48．

[9]李龙云，胡博，谢开贵，等．基于离散傅里叶变换的孤岛型微电网混合储能优化配置[J] ．电力系统自动化，2016，40(12):108-116．

LI Longyun，HU Bo，XIE Kaigui，et al．Capacity optimization of hybrid energy storage systems in isolated microgrids based on discrete Fourier transform[J] ．Automation of Electric Power Systems，2016，40(12):108-116．

[10]蒋平，熊华川．混合储能系统平抑风力发电输出功率波动控制方法设计[J] ．电力系统自动化，2013，37(1):122-127．

JIANG Ping，XIONG Huachuan．A control scheme design for smoothing wind power fluctuation with hybrid energy storage system[J] ．Automation of Electric Power Systems，2013，37(1):122-127．

[11]刘方，杨秀，时珊珊，等．不同时间尺度下基于混合储能调度的微网能力优化[J] ．电网技术，2014，38(11):3079-3087．

LIU Fang，YANG Xiu，SHI Shanshan，et al．Hybrid energy storage scheduling based microgrid energy optimization under different time scales[J] ．Power System Technology，2014，38(11):3079-3087．

[12]桑丙玉，王德顺，杨波，等．平滑新能源输出波动的储能优化配置方法[J] ．中国电机工程学报，2014，34(22):3700-3706．

SANG Bingyu，WANG Deshun，YANG Bo，et al．Optimal allocation of energy storage system for smoothing the output fluctuations of new energy[J] ．Proceedings of the CSEE，2014，34(22):3700-3706．

[13]丁明，林根德，陈自年，等．一种适用于混合储能系统的控制策略[J] ．中国电机工程学报，2012，32(7):1-6．

DING Ming，LIN Gende，CHEN Zinian，et al．A control strategy for hybrid energystorage systems[J] ．Proceedings of the CSEE，2012，32(7):1-6．

[14]谢兼达，邱晓燕，任立，等．计及直流配电效益的混合储能系统容量配置模型[J] ．电力建设，2016，37(5):28-33．

XIE Jianda，QIU Xiaoyan，REN Li，et al．Capacity configuration model of hybrid energy storage system considering DC distribution benefit[J] ．Electric Power Construction，2016，37(5):28-33．

[15]马速良，蒋小平，马会萌，等．平抑风电波动的混合储能系统的容量配置[J] ．电力系统保护与控制，2014，42(8):108-114．

MA Suliang，JIANG Xiaoping，MA Huimeng，et al．Capacity configuration of the hybrid energy storage system for wind power smoothing[J] ．Power System Protection and Control，2014，42(8):108-114．

[16]孙承晨，袁越．基于经验模态分解和神经网络的微网混合储能容量优化配置[J] ．电力系统自动化，2015，39(8):19-26．

SUN Chengchen，YUAN Yue．Capacity optimization of hybrid energy storage systems in microgrid using empirical mode decomposition and neural network[J] ．Automation of Electric Power Systems，2015，39(8):19-26．

[17]易林，娄素华，吴耀武，等．基于变寿命模型的改善风电可调度性的电池储能容量优化[J] ．电工技术学报，2015，30(15):53-59．

YI Lin，LOU Suhua，WU Yaowu，et al．Optimal battery capacity based on lifetime predication for improving the schedulability of the wind power [J] ．Transactions of China Electrotechnical Society，2015，30(15):53-59．

(编辑 张小飞)

Capacity Configuration of Hybrid Energy Storage System Based on Double Layer Power Decomposition

WANG Yue ,LUY Lin , ZHU Yuwei

(Intelligent Electric Power Grid Key Laboratory of Sichuan Province (School of Electric Engineering and Information, Sichuan University), Chengdu 610065, China)

Suitable energy storage can be configured for the wind power plant to stabilize the fluctuations of wind power and improve the power quality of wind power. Based on the historical data of wind power output, this paper proposes a double layer power decomposition method. The first layer adopts moving average method to decompose the power of the grid-connected power and hybrid energy storage system, according to the wind power grid connected indicators in China. The second layer uses spectrum analysis method and Fourier transform to decompose the reference power of hybrid energy storage system into low frequency component and high frequency component, which are distributed to the battery and the super capacitor, respectively. Considering the state of charge of energy storage equipment and the cycle life of the battery, this paper establishes the capacity optimization model of the hybrid energy storage system, which takes the minimum annual comprehensive cost as the optimization goal. The simulation results verify the feasibility of the double layer power decomposition method, and prove that the hybrid energy storage system is superior to the single type energy storage system in performance and economy.

double layer power decomposition; moving average method; hybrid energy storage; spectrum analysis; the cycle life; annual comprehensive cost

四川省应用基础研究计划资助项目(2015JY0128)

TM 614

A

1000-7229(2016)12-0061-07

10.3969/j.issn.1000-7229.2016.12.008

2016-08-11

王跃(1989)，男，硕士研究生，主要研究方向为混合储能在主动配电网中的应用，配电网自动化；

吕林(1963)，男，教授，硕士生导师，主要研究方向为分布式发电，配电网自动化；

朱雨薇(1992)，女，硕士研究生，主要研究方向为混合储能在主动配电网中的应用，配电网自动化。