非线性弹性地基上悬臂管道的参数振动

李云东, 杨翊仁, 文华斌

(1.四川理工学院 理学院，四川 自贡 643000； 2．西南交通大学 力学与工程学院，成都 613001;3.四川理工学院 机械工程学院，四川 自贡 643000)

非线性弹性地基上悬臂管道的参数振动

李云东1,2, 杨翊仁2, 文华斌3

(1.四川理工学院 理学院，四川 自贡 643000； 2．西南交通大学 力学与工程学院，成都 613001;3.四川理工学院 机械工程学院，四川 自贡 643000)

首先建立了非线性弹性地基上悬臂输流管在振荡流作用下的运动方程，应用Galerkin方法将运动控制偏微分方程离散成常微分方程组。采用数值方法着重讨论了平均流速、脉动幅值、脉动频率和地基剪切刚度等参数对系统动力学行为的影响。 结果表明：以平均流速为分岔参数系统会出现拟周期运动，然后是周期运动， 接着出现混沌运动；以脉动幅值为分岔参数系统发生周期2，周期4，周期8，然后进入混沌运动；以脉动频率为分岔参数系统先发生拟周期运动，然后在二阶次谐波附近发生混沌运动。另外，地基剪切刚度对系统地周期运动和混沌有抑制作用，随着剪切刚度增大，系统从混沌状态演化到周期状态，直至稳态。

悬臂输流管；弹性地基；周期运动；混沌运动

输流管道动力学问题，一直以来是学术研究热点问题之一，到目前为止，已得到了很多研究成果，有兴趣的读者可以参阅由著名学者PAIDOUSSIS[1]撰写的专著。已有的文献[2]表明悬臂输液管道在流速足够大的定常流作用下会发生颤振失稳，但是如果内流为振荡流，即使流速较小(远小于发生的动态失稳临界速度)，系统也有可能因参数共振而使系统失稳。管内为振荡流的振动问题研究，目前也有一些比较好的结论。PANDA等[3]应用多尺度法研究在振荡流作用下简支输液管的参数共振行。NAMACHCHIVAYA等[4-5]应用平均法研究了在振荡流作用下简支输液管的次谐波共振和组合共振。金基铎等[6]用平均法进一步分析了参数共振的共振区域，用数值方法研究了在失稳区域的动力学现象。WANG[7]用数值方法研究了平均流速较大的情况下脉动内流作用下铰支管的动力学行为。以上都是简支输液管的动力学分析，对于悬臂输液管脉动内流得分析相对来说较少。PAIDOUSSIS等[8]应用Bolotin 方法和Floquet理论研究了悬臂输液管在脉动内流下的参数共振和组合共振区域失稳边界。SEMIER等[9]基于范式理论和中心流形理论研究了悬臂输液管在脉动内流作用下，平均流速接近与临界流速时系统的稳定性及动力学现象。唐冶等[10]研究了非线性弹性支撑悬臂输液管在参数激励和外激励联合作用下的非线性动力学行为。张紫龙等[11]基于Galerkin法研究了在基础激励作用下非线性弹性地基上悬臂管道的非线性动力学行为。蒲育等[12]研究了Winkler-Pasternak弹性地基上功能梯度梁的自由振动。

本文首先建立了非线性弹性地基上脉动内流悬臂管道的动力学方程，使用Galerkin方法 对控制方程进行离散，采用数值方法研究了参数激励作用下非线性弹性地基上悬臂输流管道的动力学行为。 着重讨论了平均流速、脉动幅值、脉动频率及地基剪切刚度对动力学特性的影响。

1 输液管运动微分方程

考虑如图1所示的非线性弹性地基上输液管道,U为管内流体。管道采用Bernoulli-Euler梁模型来描述,y(x,t)是管道的中心线横向位移,x为沿管道长度方向的位置坐标，kG,C,k1,k2分别表示剪切刚度，黏性阻力，等效线性刚度和等效非线性刚度。非线性弹性地基上非稳态流悬臂输液管为

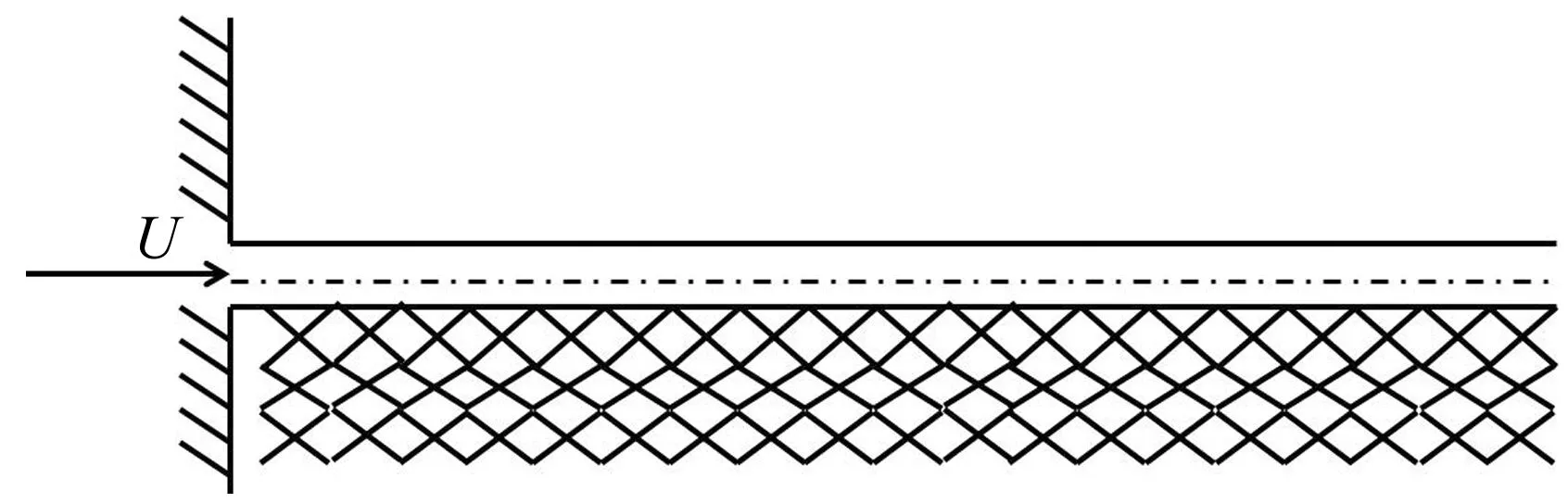
图1 非线性弹性地基上输液管道示意图Fig.1 Schematic of cantilevered pipe conveying fluid rested on nonlinear elastic foundation

(1)

式中：EI为管道抗弯刚度，E*为黏弹性系数，M和m分别为单位长度上流体质量和管质量。

地基支承力：

(2)

引入无量参数：

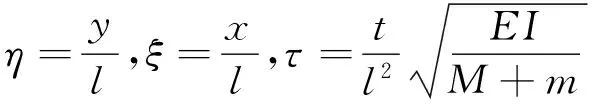
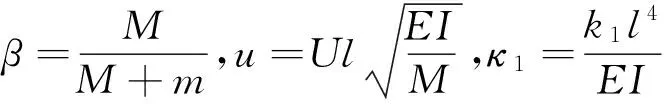
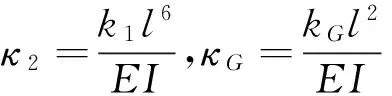
(3)

控制方程式(1)的无量纲形式为

(4)

无量纲化的脉动速度表达式：

u=u0(1+μsinωτ)

(5)

把式(5)代入式(4)式得：

κ2η3=0

(6)

无量纲边界条件为：

η(0,t)=0,η′(0,t)=0,

η″(0,t)=0,η‴(0,t)=0

(7)

在这里， 应用迦辽金法来离散方程式(5)，以无阻力悬臂梁模态函数φr(ξ)作为基函数，

这样，管的振动响应表示为

(8)

把式(8)代入式(6) ，然后在[0，1]区间上对方程两边进行积分，利用模态函数的正交性，可得离散后的常微分方程组

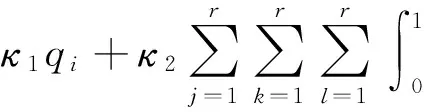
(9)

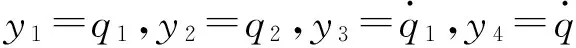
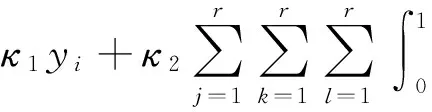
i=1,2

(10)

求解此方程组，可得系统的动力学响应。

2 数值计算和分析

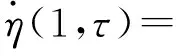
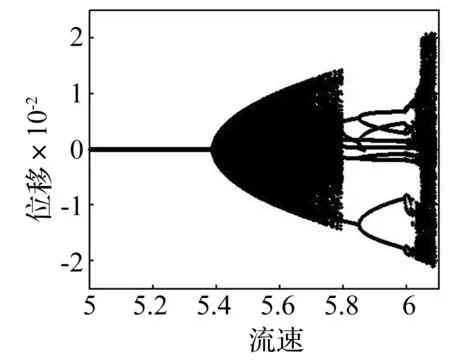
图2 流速的分岔图Fig.2 Bifurcation diagram of flow velocity

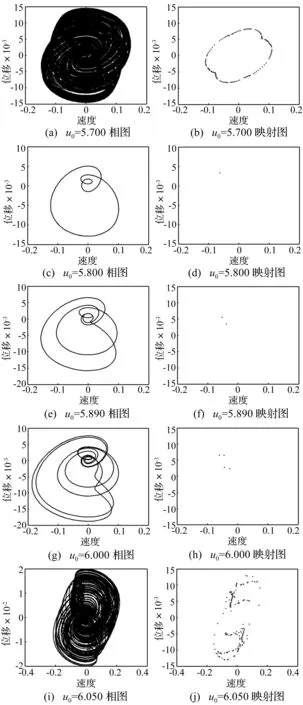
图3 不同流速下相图和庞加莱映射图Fig.3 The phase diagram and Poincare maps diagram with different flow velocity

首先，考察地基kG=0.0时， 脉动速度幅值和频率分别为μ=0.4,ω=5.0，以平均流速u0为分岔参数的系统的响应分岔图，如图2所示。从分岔图可以看到，当流速u0<5.385时，系统不会发生失稳，位移幅值收敛于零。当5.3856.096后，从数值计算可以看，系统发散了。

图4 展示了亚临界速度下即取流速为u0=5.6，并且脉动激振频率取为二阶频率的2倍，即ω=2ω2，系统随脉动幅值变换的分岔图。当 0≤μ≤0.006时， 系统位移幅值为零，系统每有出现失稳。当0.006≤μ≤0.274，随着脉动幅值增加，系统位移幅值也增加，当脉动幅值到达μ=0.212，系统位移幅值有跳跃现象。 当脉动幅值在这个过程中，由图5(a)～(f)在各脉动幅值时的相图和Poincare映射图可判断，系统发生了周期2，周期4，周期8等倍周期分岔。当脉动幅值在0.274<μ≤0.339时，由图5(g)和(h)可判断系统发生了混沌运动。当μ>0.339后，系统发散。最后，在此参数选择下，系统将发生由倍周期到混沌的运动。

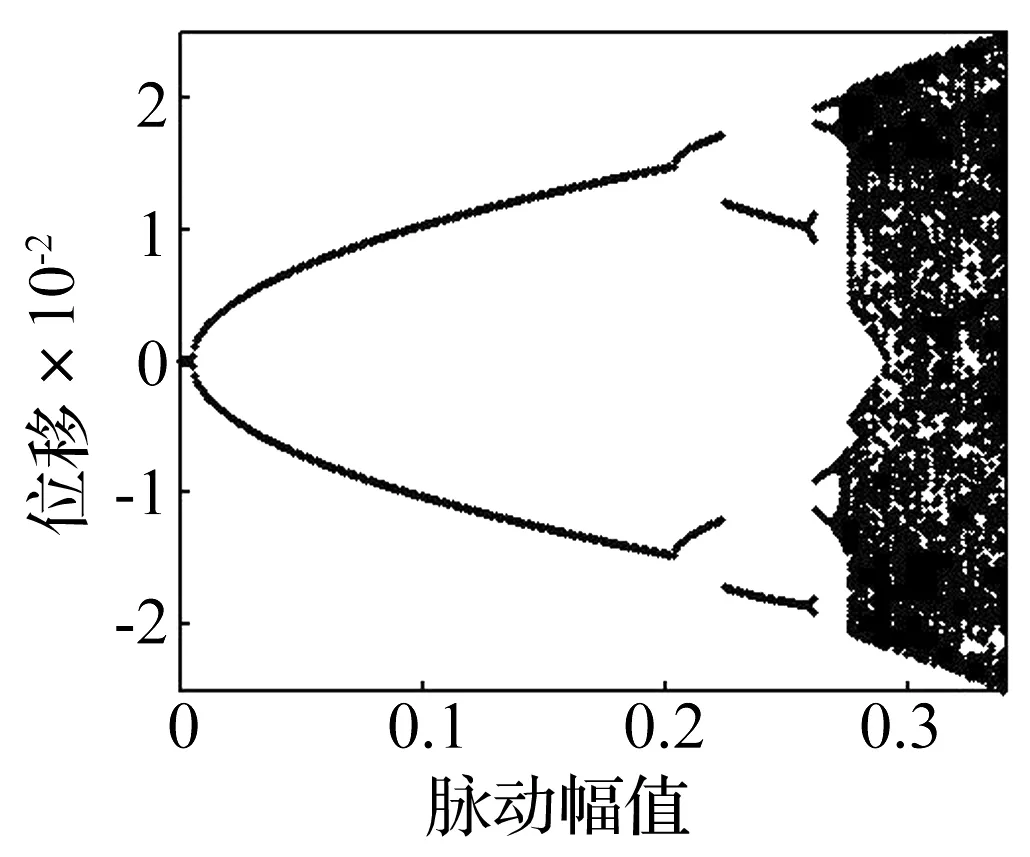
图4 脉动幅值的分岔图Fig.4 The bifurcation diagram of fluctuation amplitude

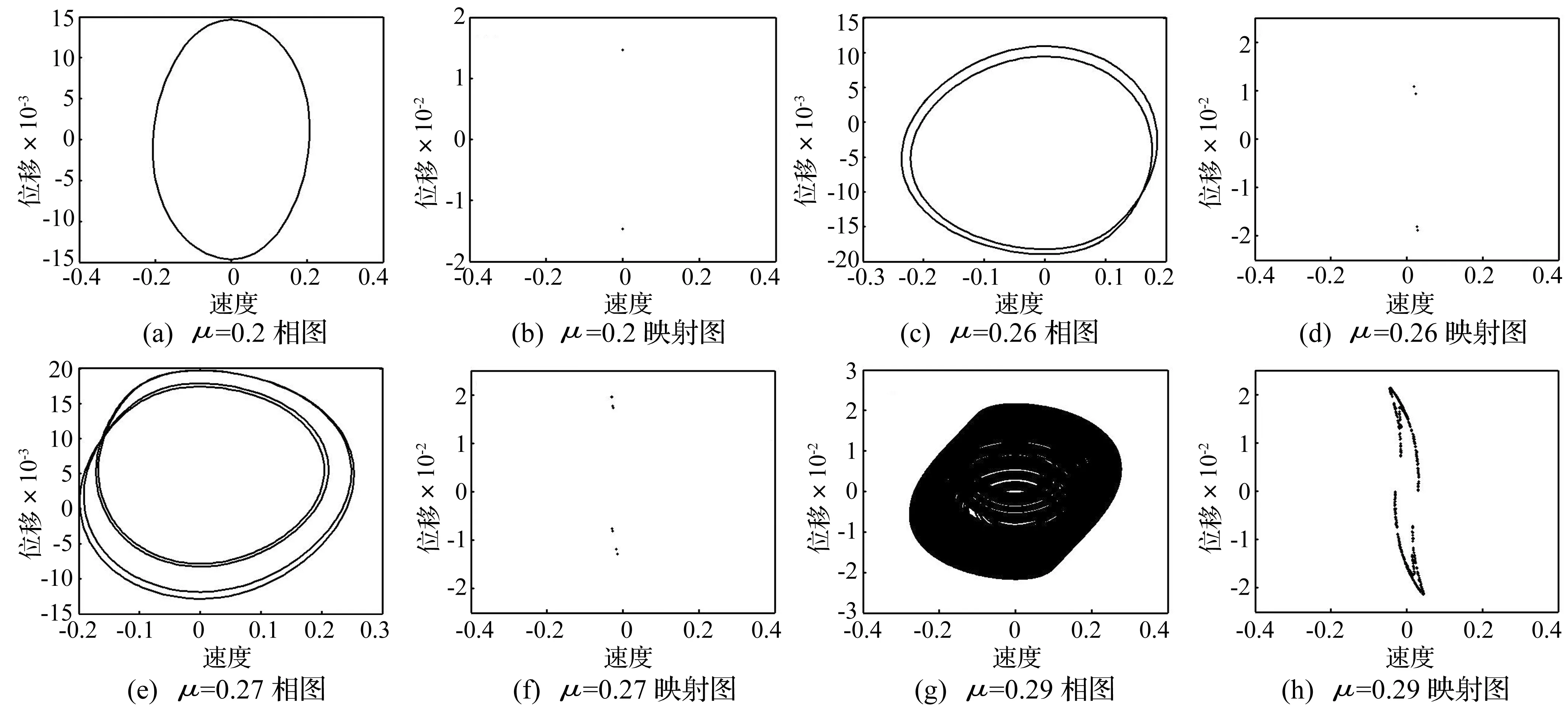
图5 不同脉动幅值的相图和庞加莱映射图Fig.5 The phase diagram and Poincare maps diagram with different fluctuation amplitude

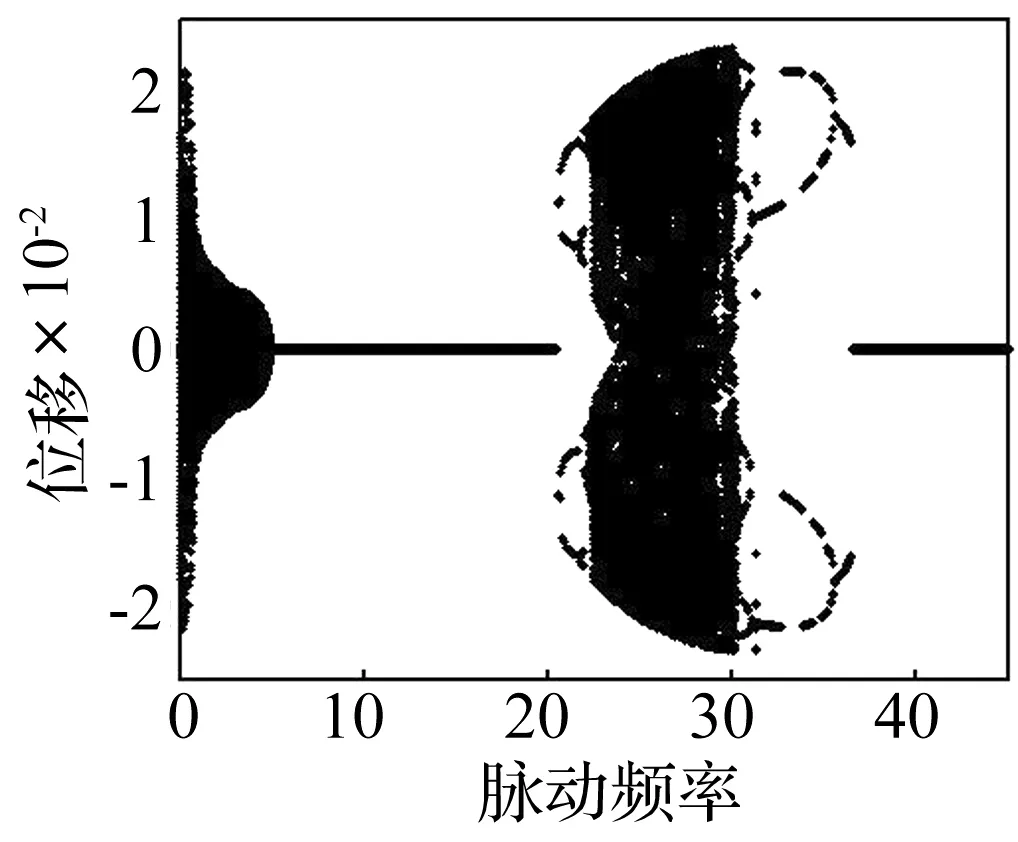
图6 脉动频率的分岔图Fig.6 The bifurcation diagram of fluctuation frequency

图6 展示了位移随脉动频率变化的分岔图，其参数选择为：u0=5.6,μ=0.3，其它参数选择不变。从分岔图可以看出，当0<ω<5.0时，系统主要表现为拟周期运动，这个区域主要是系的主共振和超谐波共振区域，系统随频率的增加，拟周期运动的幅值减小，最后消失；当区域20.0<ω<35.5时，系统为二阶振型的1/2次谐波共振区域，系统首先是周期运动，周期1，周期2，周期4运动，然后系统进入混沌运动，经过一个相对较宽的区域，系统又出现周期运动，由周期4，周期2，周期1，总的来说，在这个区域系统是由周期运动到混沌运动，然后又是退化到周期运动。另外，需要说明的是，在由稳态到周期运动，或者由周期运动到稳态过程中，从分岔图看出系统有跳跃现象。在其它区域内，系统处于稳定状态。 图7展示了在ω=0.8和ω=28.0两个区域内典型的相图和Poincare映射图，由此可以证明其运动行为。

在以上的分析中，弹性地基参数kG=0.0，下面我们将对这个参数对系统的位移幅值影响进行研究。图8展示了地基剪切力对系统位移的影响，选取参数为：u0=5.6,μ=0.3,ω=28.0。从图8可以看出，地基剪切力对系统的动力学行为有很大的影响。在本参数条件下， 当0≤kG≤0.93时，系统表现为混沌运动；当0≤kG≤1.17时，系统为多周期运动；当1.15≤kG≤1.46时，系统再次表现为混沌运动。当1.46≤kG≤11.32，系统有多周期运动，周期8，周期4，周期2运动，最后稳态运动。因此，地基剪切刚度对参数激振作用下输流管-地基系统的混沌运动和概周期运动有很好的抑制作用，这结论与文献[11]的结论是一致的。基于篇幅的原因，在这里略去相图和Ponicare映射图。

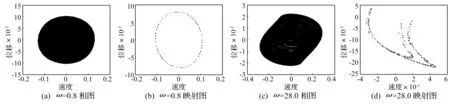
图7 不同脉动频率的相图和庞加莱映射图Fig.7 The phase diagram and Poincare maps diagram with different fluctuation frequency

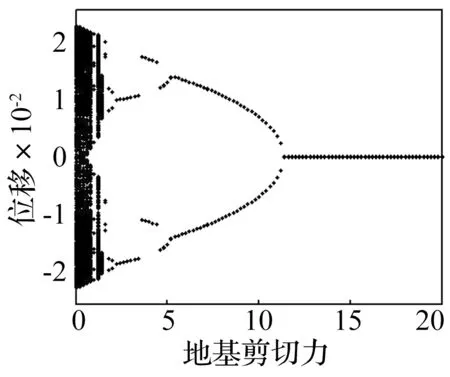
图8 地基剪切力的分岔图Fig.8 The bifurcation diagram of foundation shear force

3 结 论

本文给出了非线性弹性基上悬臂输液管在周期振荡流作用下的非线性运动方程，采用数值方法研究了在不同参数下的非线性动力学响应，揭示了系统丰富的动力学现象。

(1)系统以流速u0为分岔参数时，系统会首先出现拟周期运动，然后是周期运动， 接着出现混沌运动，最后系统发散。

(2)系统以脉动幅值μ为分岔参，并且设脉动频率ω为二阶频率ω2的二倍，即二阶次谐波共振，发现系统由周期2，周期4，周期8，然后进入混沌运动，最后发散。 周期运动过程中有跳跃现象。

(3)系统以脉动频率ω为分岔参数， 在本文选择的参数值下，系统首先出现一阶振型主共振和超谐波共振，会导致系统出现拟周期运动，而在二阶振型的次谐波共振会导致系统发生混沌运动。

(4)地基剪切力是对的动力学行为是有影响的。当剪切刚度足够大时，系统可能一直处于稳态。

[1] PAIDOUSSIS M P. Fluid-structure interactions: slender structures and axial flow [M]. London: Academic Press, 1998.

[2] LI G, PAIDOUSSIS M P. Stability, double degeneracy and chaos in cantilevered pipes conveying fluid [J]. International Journal of Non-linear Mechanics, 1994, 29(1): 83-107.

[3] PANDA L, KAR R. Nonlinear dynamics of a pipe conveying pulsating fluid with combination, principal parametric and internal resonances [J]. Journal of Sound and Vibration, 2008, 309(3): 375-406.

[4] NAMACHCHIVAYA N S. Non-linear dynamics of supported pipe conveying pulsating fluid—I. Subharmonic resonance [J]. International Journal of Non-linear Mechanics, 1989, 24(3): 185-196.

[5] NAMCHCHIVAYA N S, TIEN W. Non-linear dynamics of supported pipe conveying pulsating fluid—II. Combination resonance [J]. International Journal of Non-linear Mechanics, 1989, 24(3): 197-208.

[6] 金基铎, 杨晓东, 尹峰. 两端铰支输流管道在脉动内流作用下的稳定性和参数共振 [J]. 航空学报, 2003, 24(4): 317-322. JIN Jiduo, YANG Xiaodong, YIN Feng. Stability and parametric resonances of a pinned-pinned pipe conveying pulsating fluid[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(4): 317-322.

[7] WANG L. A further study on the non-linear dynamics of simply supported pipes conveying pulsating fluid [J]. International Journal of Non-linear Mechanics, 2009, 44(1): 115-121.

[8] PAIDOUSSIS M P, SUNDARARARA C. Parametric and combination resonances of a pipe conveying pulsating fluid [J]. Journal of Applied Mechanics, 1975, 42(4): 780-784. [9] SEMIER C, PAIDOUSSIS M P. Nonlinear analysis of the parametric resonances of a planar fluid-conveying cantilevered pipe [J]. Journal of Fluids and Structures, 1996, 10(7): 787-825.

[10] 唐冶, 方勃, 张业伟. 非线性弹簧支承悬臂输液管道的分岔与混沌分析 [J]. 振动与冲击, 2011, 30(8): 269-274. TANG Ye, FANG Bo, ZHANG Yewei. Bifurcation and chaos analysis of cantilever pipeline conveying fluid with nonlinear spring support[J].Journal of Vibration and Shock, 2011,30(8):269-274.

[11] 张紫龙, 唐敏, 倪樵. 非线性弹性地基上悬臂输流管的受迫振动 [J]. 振动与冲击, 2013, 32(10): 17-21. ZHANG Zilong, TANG Min, NI Qiao. Forced vibration of a cantilever fluid-conveying pipe on nonlinear elastic foundation[J]. Journal of Vibration and Shock,2013,32(10):17-21.

[12] 蒲育，滕兆春. Winkler-Pasternak弹性地基FGM梁自由振动二维弹性解[J].振动与冲击,2015,34(20):74-79. PU Yu, TENG Zhaochun. Two-dimensional elasticity solutions for free vibration of FGM beams resting on Winkler-Pasternak elastic foundations[J].Journal of Vibration and Shock,2015,34(20):74-79.

Parametric vibration of a cantilevered pipe conveying pulsating fluid on a nonlinear elastic foundation

LI Yundong1, 2, YANG Yiren2, WEN Huabin3

(1. School of Science, Sichuan University of Science & Engineering, Zigong 643000, China;2. School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China;3. College of Mechanical Engineering, Sichuan University of Science & Engineering, Zigong 643000, China)

The motion equation of a cantilevered pipe conveying pulsating fluid on a nonlinear el-astic foundation was constructed, and was discretized into ordinary differential equations by the Galerkin method. The effect of parameters including mean flow velocity, fluctuation amplitude, fluctuation frequency and shear stiffness on the nonlinear behavior of the system was investigated by a numerical method. The results show that the system can present quasi periodic motion, periodic motion, and chaotic motion if the mean flow velocity is used as the bifurcation parameter; the system presents the period-2, period-4, period-8, and chaotic motion if the fluctuation amplitude is used as the bifurcation parameter; the system firstly shows quasi-periodic motion, then chaotic motion nearby second sub harmonic if the fluctuation frequency is used as bifurcation parameter. Furthermore, foundation shear stiffness can suppress the period motion and chaotic motion of the system. With shear stiffness increasing, chaos state of the system gradually changes into periodic motion until a stable state is obtained.

cantilevered pipe conveying fluid; elastic foundation; period motion; chaotic motion

四川省科技厅(2013TD004);四川理工学院校基金(2015KY02)

2015-08-19 修改稿收到日期：2015-11-24

李云东 男，博士生，1979年生

杨翊仁 男，教授，1959年生

O322

A

10.13465/j.cnki.jvs.2016.24.003