土质地基道路引起既有隧道变形的解析估算法探索

莫阳

（悉地（苏州）勘察设计顾问有限公司,江苏 苏州 215123）

土质地基道路引起既有隧道变形的解析估算法探索

莫阳

（悉地（苏州）勘察设计顾问有限公司,江苏 苏州 215123）

城市地铁迅猛发展引发道路建设期及运营期对既有地铁隧道的保护问题，以提供简便实用的方法对道路施工影响既有隧道进行分析为目的，基于等效原理和连续性原理并运用弹性力学和土力学理论，确定隧道变形与周围土体变形之间的关系，建立附加荷载作用下土质地基中隧道变形的解析算法，导出道路施工对隧道变形影响程度的验算判别式。

道路工程；解析估算法；隧道变形；土质地基

0 引言

城市轨道交通具有引导城市空间发展方向、适度扩散、又防止过度扩散的功能[1]，因规划引导可先于城区建成，主要线位形态与城市干路叠合。新建道路横跨、平行且邻近既有隧道，或者既有隧道的上覆老路翻修，均会引起既有隧道的附加变形。既有隧道受基坑工况影响的研究较多，主要用有限元法估算隧道变形[2-5]。土质地基上修筑道路，路床基底开挖较浅并用分层压实法进行后续施工，既有隧道受反复加、卸载影响工况的研究较少[6]，下面根据土体变形与附加应力、隧道变形与周围土体变形的关系，尝试建立隧道变形的解析估算方法。

1 土体内的附加应力

将土质地基视作均质弹性体[7]，隧道简化成矩形截面并视为土体受到的约束，考察有、无隧道情形的土体内应力。

图1中（a）与（c）、（b）与（d）受力状况都只差外荷载p，按叠加原理，加载时土体内的附加应力在有、无隧道时相同；同理，卸载时土体内的附加应力在有、无隧道时相同。卸载后再以相同荷载集度进行加载，按叠加原理，卸载产生的附加应力效应与加载相同。

图1土体内应力

图2 为加载情形附加应力计算图式，根据土力学[8]及弹性力学[9]，土体内任一点附加应力为荷载集度乘系数，与变形估算相关的附加应力系数分析结果如下：

图2 附加应力计算图式

路、隧交叉时，隧道截面位置深度z处的竖向最大附加正应力系数为

路、隧平行时，隧道轴线在深度z投影处的竖向最大附加正应力系数为

路、隧平行时，隧道轴线在深度z投影处的附加剪应力系数为

同一深度z处，荷载作用面下很小深度范围内集中荷载的效应大一些，大于某个临界深度后均布荷载的效应更大并随深度的增加迅速增大。集中荷载出现在施工过程中，作用效应呈瞬时性和弹性，估算变形时可不考虑。

水平向荷载出现在汽车制动过程中，其最大值与汽车重量之比为a/g（a为汽车制动时的减速度最大值取2.5 m/s2[10]，g为重力加速度取9.8 m/s2），水平摩擦力产生的水平向应力集中于面层内，在面层底部就降到水平拉力的7.1%[10]，在面层以下水平向荷载作用效应不到竖向荷载的2%，可忽略不计。

2 隧道变形与附加应力的关系

与土相比隧道可视为无限长刚体，与位移相比隧道自身变形可忽略不计，隧道与土体之间不能产生脱空，其变形可认为与周围土体的变形相同。隧道结构体底面以上的土体基本不影响隧道竖向变形，隧道竖向变形以结构体底面以下的土体竖向变形度量；隧道水平向变形以结构侧面以外的土体水平向变形度量。

2.1 隧道竖向变形

土体竖向变形分为加载沉降和卸载回弹，总沉降中的瞬时沉降以修正系数反映[7]不单独计算，次固结沉降占总沉降的比例很小而不考虑[8]。

图3为加载情形土体竖向变形计算图式，设隧道结构体底面以下各土层重度为γi，i＝1，2，…，n。

图3 隧道结构体底面下土体竖向变形计算图式

路、隧交叉时，Oz轴线上深度0～z范围内的竖向平均附加正应力系数为

路、隧平行时，隧道纵向轴线位置深度0～z范围内的竖向平均附加正应力系数为

根据规范[11]推荐方法，3种荷载作用时的隧道变形量计算公式为

纯加载的竖向变形量

纯卸载时的竖向回弹变形量

卸载再加载时的竖向再压缩变形量

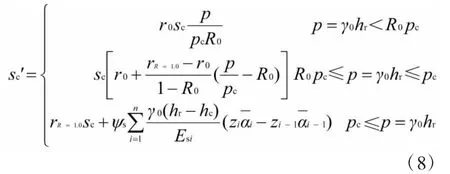
式（6）～式（8）中：ψs、ψc分别为沉降量、回弹量计算经验系数；γ0、γc分别为填土、挖土的平均重度，kN/m3；h0、hc、hr分别为纯加载、纯卸载、卸载再加载的荷载换算土高度，m；Esi、Eci分别为隧道结构体底面以下第i层土的压缩模量、回弹模量，MPa；zi为原地面至第i层土底面的距离，m为原地面至第i层土底面范围内平均附加正应力系数；r0为临界再压缩比率；R0为临界再加荷比；rR=1.0为对应于再加荷比R=1.0时的再压缩比率；pc＝γchc。

2.2 隧道水平向变形

以加载情形为例，图4为隧道变形分析图式，路、隧交叉时取平行且与yOz平面距离l、厚度δ为无限小的2个隧道斜截面薄片为单元体，路、隧平行时取平行且与xOz平面距离l、厚度δ为无限小的2个隧道正截面薄片为单元体。

图4 隧道变形分析图式

由附加应力对称性，路、隧交叉时，单元体叠加后在平行于及垂直于隧道纵向轴线的平面内所受合力为零，隧道在水平面内不会发生平移；路、隧平行时，若道路中心线与隧道纵向轴线间的平距D不为零，隧道在垂直于纵向轴线的水平方向合力不为零，会发生平移。

施加的外荷载作用（包括加载和卸载）的合外力矩为零，隧道整体或局部不会在水平面内或绕自身纵向轴线转动。

以加载情形为例，图5为隧道水平向变形分析图式，隧道正截面周界顶边上的点1、2、3处的土体水平变形量的关系为u1＞u2＞u3，隧道在附加应力作用下无自身变形量，隧道与土体间必然存在相对滑移。由土体变形连续性，隧道水平向变形应介于u1和u3之间，取顶边中点处的土体水平变形量作为对隧道平移的量度。

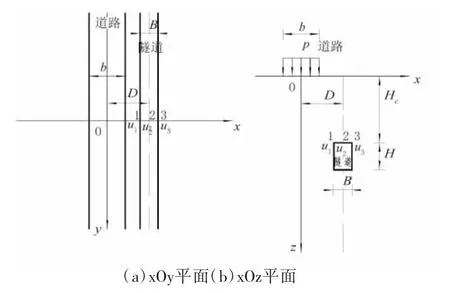
图5 隧道水平向变形分析图式

按平面应变状态[9]，考虑土的非完全弹性而引入水平变形经验系数ψh，隧道平移量um为

式中：E为隧道顶板以上土体的当量变形模量，MPa；ν为隧道顶板以上土体的当量泊松比；γ为路基填土或挖除土体的平均重度，kN/m3；h为加载换算填土高度或挖土高度，m。

3 道路施工和运营验算

根据控制变形不得超过允许变形的原则，按式（6）～式（9）得到总变形验算判别式和逐次变形验算判别式列于表1和表2。

按照相关文献[12]并结合道路施工和运营特点，总允许变形和逐次允许变形的建议值见表3。

3.1 临界距离

以单轴双轮组为代表，双轮之间距离很近可看作一个大的单轮，轴两端轮中心之间距离取2 m，静动应力比取n时的荷载影响深度为考虑轴载反复作用形变积累导致影响区下移、道路施工和运营期的不利状况，设计路面与隧道的临界竖向距离hvmin为

式中：Zai（i＝1，2，3）为路基施工期、路面施工期、道路运营期的荷载影响深度，m；hb为路床厚度，m，路面施工期和道路运营期取0；hs为保护土层厚度，m；hp为路面厚度，m。设计路面与隧道顶面的临界竖向距离见表4。深度z处的水平向应力最大值点位由条件x=z确定，简化成平面问题，静动应力比取n时的荷载影响水平距离为隧道的临界水平距离lhmin为设计道路边线与

式中：Xai（i＝1，2，3）为路基施工期、路面施工期、道路运营期的水平影响距离，m。

K0取建议参考值范围[8]内的中值时，临界水平距离计算值见表5。

当满足竖向或水平临界距离之一时，可认为道路施工和运营不会对既有隧道产生影响。

表1 总变形验算判别式

表2 逐次变形验算判别式

表3 受道路影响的既有隧道变形允许值（单位：mm）

表4 设计路面与隧道顶面的临界竖向距离（单位：m）

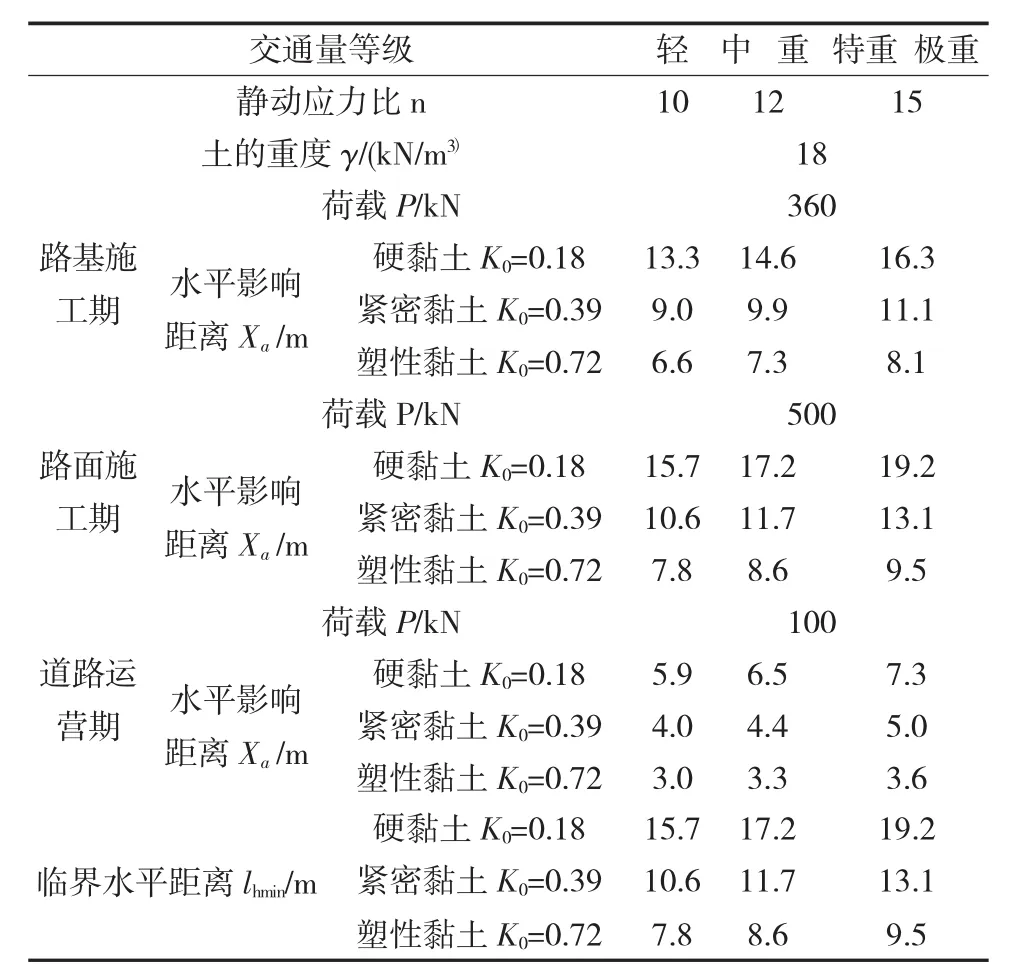
表5 设计道路边线与隧道侧面的临界水平距离（单位：m）

3.2 压实施工方式的适用性

设最大施工机具的动荷载为P，简化成平面问题后分别求得竖向变形最小值和水平向变形最大值，即得压实施工方式适用性判别式：

隧道结构体水平面投影在道路施工范围内

隧道结构体水平面投影在道路施工范围外

式（12）中H0'为隧道结构顶面与压实作用面的竖向距离，式（13）则要求在隧道所处深度范围内存在D0为压实作用点与隧道的水平向距离。

4 结 语

通过分析道路层铺压实施工的特点、荷载作用与既有隧道变形之间关系，得到相应状况下以施加荷载的解析函数表示的既有隧道变形，基于解析法数学处理简单、易于实现软件计算的特点，在设计阶段估计既有隧道受影响程度、施工阶段控制工艺要求方面具有实用参考价值。

[1]毛保华,陈绍宽,刘智丽.城市轨道交通规划与设计（第二版）[M].北京:人民交通出版社,2011.

[2]师晓权.基坑开挖对下卧隧道影响的研究[D].四川成都:西南交通大学,2008.

[3]刘小建.控制卸荷对下卧地铁隧道隆起影响的试验和研究[D].上海:同济大学,2008.

[4]王路.基坑开挖对邻近既有隧道的影响分析[D].北京:北京交通大学,2009.

[5]童伟.深基坑开挖对邻近既有隧道力学效应影响规律研究[D].四川成都:西南交通大学,2013.

[6]张健.新建铁路路基上跨既有隧道安全性评估 [J].公路工程, 2012,37(4):37-39,143.

[7]李广信.高等土力学[M].北京:清华大学出版社,2004.

[8]李广信,张丙印,于玉贞.土力学第2版[M].北京:清华大学出版社, 2013.

[9]徐芝纶.弹性力学第4版[M].北京:高等教育出版社,2006.

[10]黄兴安..公路与城市道路设计手册[M].北京:中国建筑工业出版社,2005.

[11]GB 50007-2011,建筑地基基础设计规范[S].

[12]李兴高.既有地铁线路变形控制标准研究[J].铁道建筑,2010(4): 84-88.

U416.1

A

1009-7716（2016）12-0148-05

10.16799/j.cnki.csdqyfh.2016.12.044

2016-09-06

莫阳（1969-），男，上海人，高级工程师，从事道路设计工作。