六轮全地形移动机器人越障性能分析与仿真

王超星，王殿君，陈 亚，刘占民，相 臣

（1.北京化工大学 机电工程学院，北京 100029；2.北京石油化工学院 机械工程学院，北京 102617）

六轮全地形移动机器人越障性能分析与仿真

王超星1，王殿君2，陈 亚2，刘占民2，相 臣2

（1.北京化工大学 机电工程学院，北京 100029；2.北京石油化工学院 机械工程学院，北京 102617）

针对六轮全地形移动机器人悬架机构的结构特点，构建了机器人越障过程动力学模型，对机器人的越障性能进行了分析并利用ADAMS进行了动力学仿真。首先对机器人前轮、中轮、后轮的越障过程进行了分析，进而基于达朗贝尔原理建立了机器人越障过程的动力学模型并进行了动力学分析，得出了机器人运动状态对电机输出力矩的影响。然后基于ADAMS仿真软件构建了机器人的仿真模型并进行动力学仿真，为机器人电机选型奠定了理论基础。最后移动机器人越障性能实验表明，六轮全地形移动机器人可以爬越楼梯等垂直障碍，为提高机器人适应复杂地形环境的能力提供理论依据。

六轮全地形移动机器人；动力学模型；动力学仿真

0 引言

随着机器人技术的发展，六轮全地形移动机器人以其体积小、质量轻、运动灵活、环境适应性强等优点，在石油化工企业巡检、军事侦察、灾难搜索等作业中有广泛的应用前景[1,2]。其大多数时间在斜坡、台阶、壕沟等复杂地形的环境中作业，这就需要移动机器人具有良好的灵活性和环境适应性，而越障能力的大小是衡量全地形移动机器人性能的关键参数[3,4]，因此研究移动机器人的越障原理和性能是非常有必要的。

目前，国内外已有基于动力学模型对移动机器人进行越障过程的研究。比如Liu等[5]对模块化履带式变形机器人的越障动力学模型进行了研究，并对机器人越障过程的影响因素进行了分析。于涌川等[6]对全驱动四轮机器人的越障过程模型进行了研究，并进行了动力学模型分析。除此之外冯虎田等[7]建立了六履带小型机器人部分特殊越障姿态的动力学模型，只对机器人的部分越障过程进行了分析，没有研究机器人的整个越障过程。

本文以六轮全地形移动机器人为研究对象，将移动机器人通过垂直障碍的过程分为前轮越障、中轮越障和后轮越障三个阶段，对每个阶段进行了越障过程分析并建立了机器人的动力学模型，基于ADAMS软件在虚拟环境中对移动机器人整个越障过程进行仿真，最后进行了六轮全地形移动机器人样机的越障性能实验。

1 六轮全地形移动机器人的结构及越障过程分析

六轮全地形移动机器人是通过悬架结构完成越障动作，机器人以楼梯台阶等垂直障碍为越障目标，而楼梯台阶的高度一般为150mm，因此以爬越150mm的台阶式障碍进行越障分析。

全地形移动机器人的单侧悬架结构，如图1所示。表示连杆1与连杆7的尺寸；表示连杆3与连杆6的尺寸；表示连杆2与连杆5的尺寸；与表示连杆4的两部分尺寸；表示初始状态时连杆4与机器人本体固定的铰接点到中轮中心的距离；表示车轮半径。

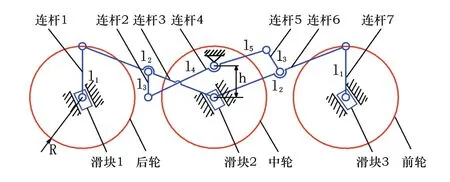
图1 机器人单侧悬架尺寸示意图

机器人越障过程模型可以简化为二维平面模型，整个越障过程可以分为三个阶段：

1）前轮越障阶段：当机器人向前行驶，直到前轮接触到障碍物，如图2(a)所示。前轮驱动连杆6绕着中轮轴心逆时针摆过一定角度，由于连杆7和障碍物的共同作用，前轮被抬起，如图2(b)所示。连杆6在车轮的驱动下继续逆时针转动，前轮不断被抬高，直到前轮完全落在垂直障碍顶部，如图2(c)所示。

2）中轮越障阶段 当机器人以如图2(c)所示的姿态移动一段距离，直至中轮接触到障碍物，如图2(d)所示。中轮驱动连杆3绕着中轮轴心逆时针摆过一定角度，连杆6绕着中轮轴心顺时针摆过一定角度，由于连杆3、连杆6和障碍物的共同作用，中轮被抬起，如图2(e)所示。在车轮的驱动下连杆3继续逆时针转动，连杆6继续顺时针转动，中轮不断被抬高，直到中轮完全落在垂直障碍顶部，如图2(f)所示。

3）后轮越障阶段 当机器人以如图2(f)所示的姿态移动一段距离，直至后轮接触到障碍物，如图2(g)所示。后轮驱动连杆3绕着中轮轴心顺时针摆过一定角度，由于连杆1和障碍物的共同作用，后轮被抬起，如图2(h)所示。连杆3在车轮的驱动下继续顺时针转动，后轮不断被抬高，直到后轮完全落在垂直障碍顶部，如图2(i)所示。

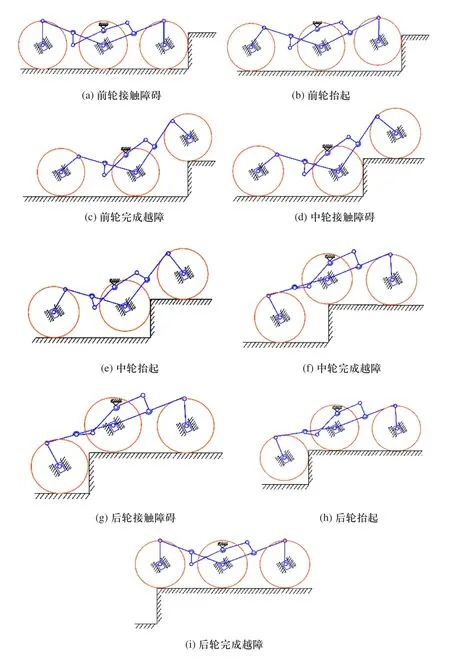
图2 机器人的越障过程

在整个越障过程中，图2(b)、图2(e)、图2(h)所示状态是机器人能否成功跨越垂直障碍的关键，所以主要建立了这几个状态的动力学模型，即前轮越障、中轮越障、后轮越障。

2 六轮全地形移动机器人越障动力学建模与分析

目前研究移动机器人动力学的方法主要有牛顿—欧拉法、达朗贝尔、拉格朗日法等[8,10]，根据全地形移动机器人的受力特点，采用达朗贝尔原理建立机器人的动力学模型。达朗贝尔原理是研究约束的质点系动力学问题的原理，它是通过引入惯性力的概念将动力学中的定理转化为静力学中的平衡关系，而且求解过程中可以充分使用静力学的各种解题技巧。

2.1 前轮越障的动力学模型

由于中轮、后轮系统对整个越障过程的影响很小，所以把它们和机器人本体作为一个整体进行研究。对前轮和本体两部分进行动力学建模与分析。建立直角坐标系，如图3所示变量分别为本体和前轮质量；分别为地面对前轮、中轮、后轮的作用力；µ为轮子与地面、障碍物的附着系数；M1、M2、M3分别为前轮、中轮、后轮受到的驱动力矩；F′x1、F′y1分别为前轮对连杆7的作用力在水平和垂直方向的投影；Fx1、Fy1分别为连杆7对前轮的作用力在水平和垂直方向的投影；表示前轮与中轮的连线与水平方向的夹角；α为前轮和中轮的连线与连杆6之间的夹角；β为前轮和中轮的连线与连杆7之间的夹角。

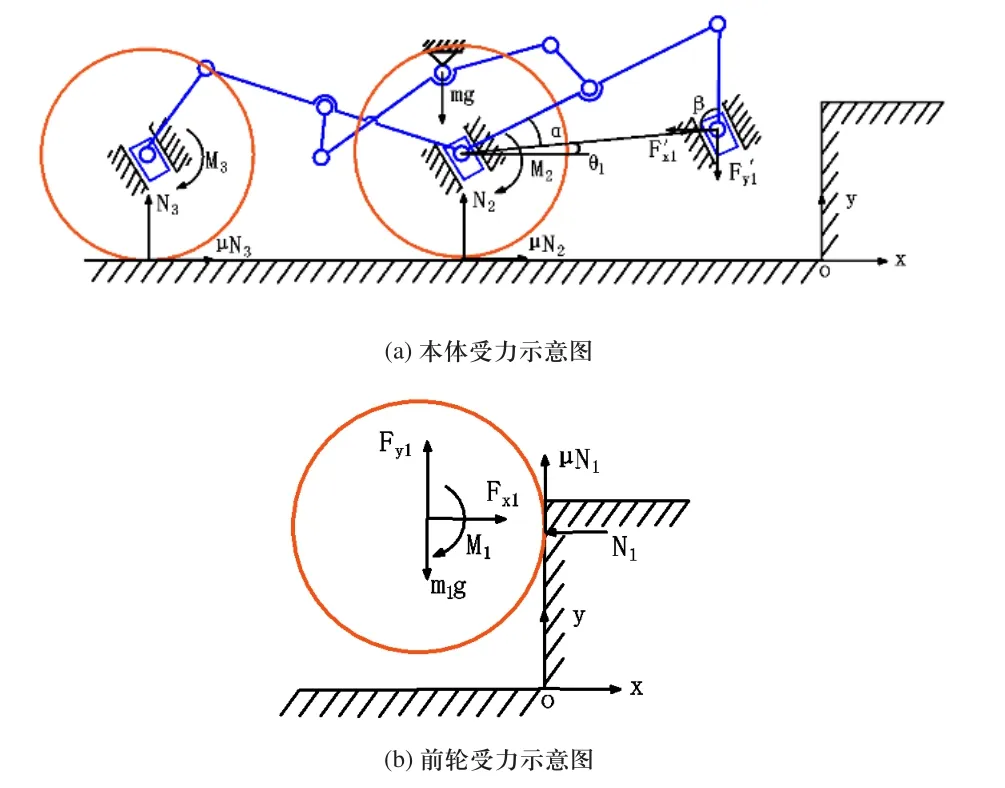
图3 前轮越障阶段机器人动力学模型

首先以机器人本体为研究对象，设前轮转动的初始角速度为ω1，角加速度为则前轮的加速度为前轮与垂直障碍物接触时的瞬时速度为：

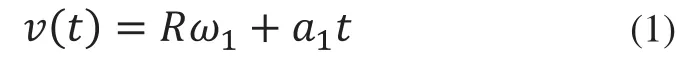
前轮与垂直障碍物接触时的瞬时位移为：

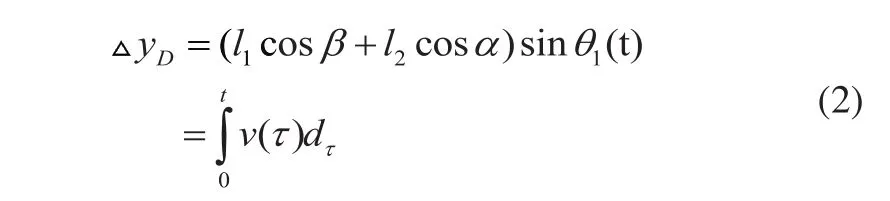
进一步整理公式(2)，得：

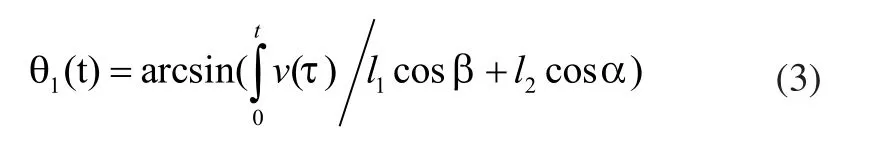
二次求导得：

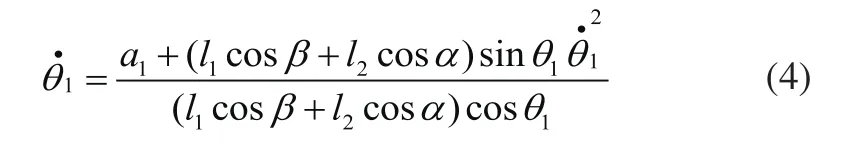
在前轮越障过程中，本体质心的转动惯量为J，质心到中轮中心的距离为H,位置由表示，可以得出：

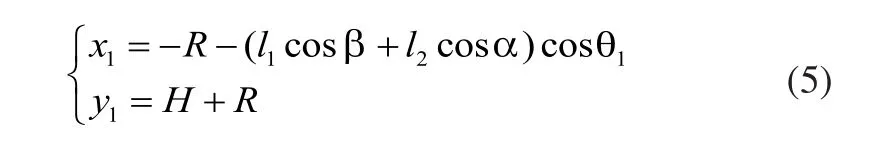
二次求导得：

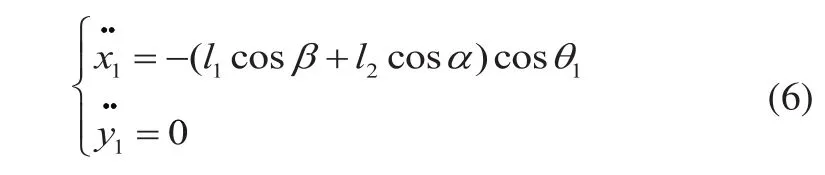
建立本体的动力学模型为：

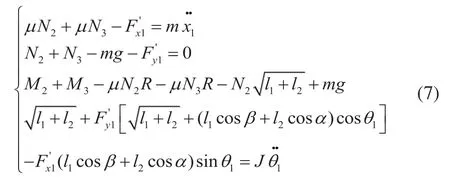
已知前轮质心在垂直方向上的速度为，转动惯量为J1，建立前轮的动力学模型为：

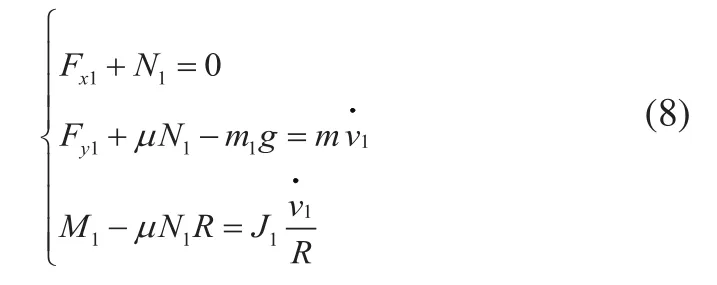
2.2 中轮越障的动力学模型

把前轮、后轮系统和机器人本体作为一个整体进行研究，对中轮和本体两部分进行动力学建模与分析。建立直角坐标系xoy，如图4所示。变量为中轮质量；分别为中轮对连杆6及连杆3的作用力在水平和垂直方向的投影；Fx2、Fy2分别为连杆6及连杆3对中轮的作用力在水平和垂直方向的投影；表示后轮与中轮的连线与水平方向的夹角；为后轮和中轮的连线与连杆3之间的夹角；γ为后轮和中轮的连线与连杆1之间的夹角。

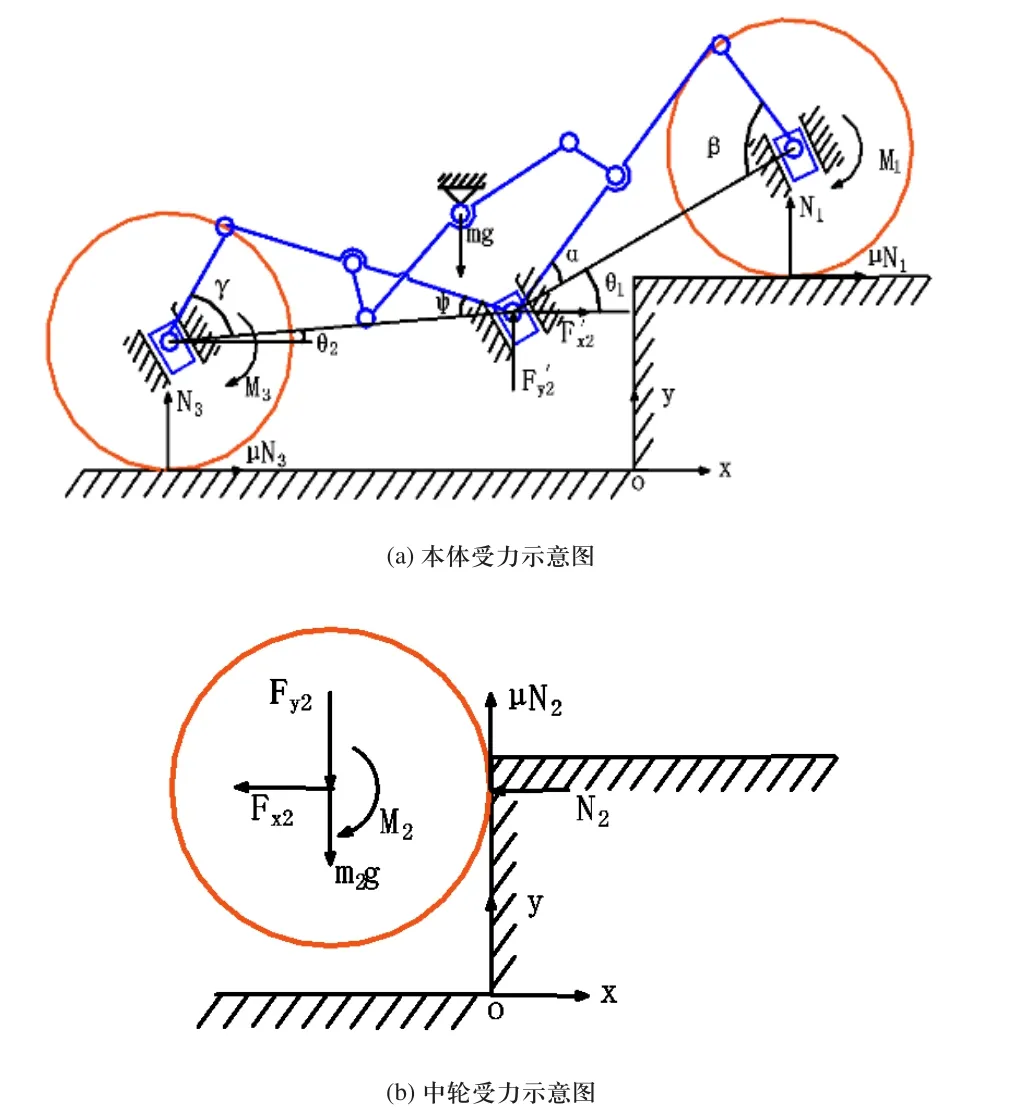
图4 中轮越障阶段机器人动力学模型

首先以机器人本体为研究对象，设中轮转动的初始角速度为ω2，角加速度为故中轮的加速度为中轮与垂直障碍接触时的瞬时速度为：

中轮与垂直障碍接触时的瞬时位移为：

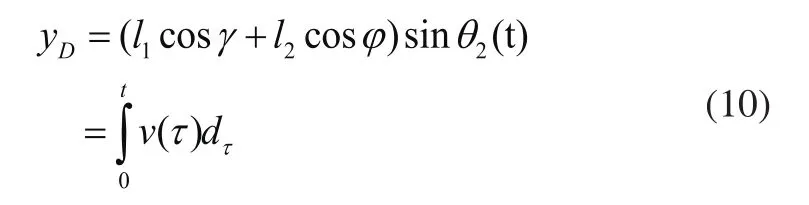
进一步整理公式(9)，得：

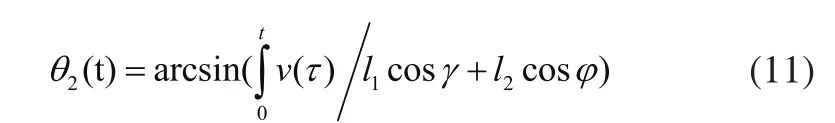
二次求导得：

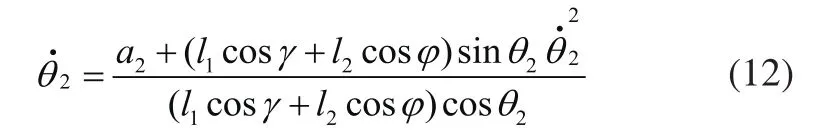
在中轮越障过程中，本体质心的转动惯量为J，质心到中轮中心的距离为H，位置由表示，可以得出：

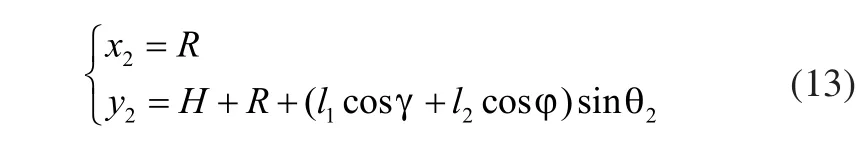
二次求导得：

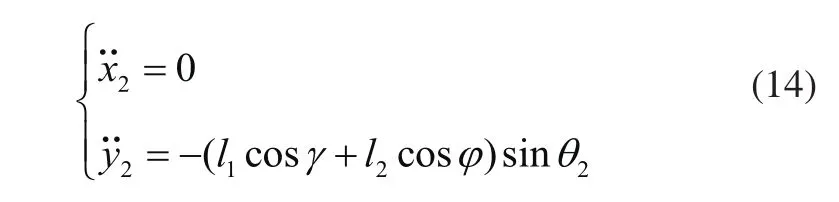
建立本体的动力学模型为：

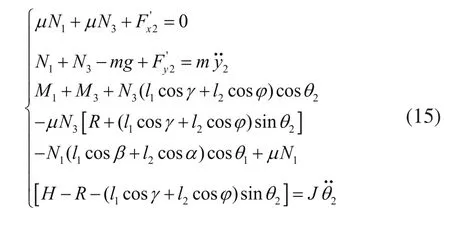
已知中轮质心在垂直方向上的速度为，转动惯量为J2，建立中轮的动力学模型为：

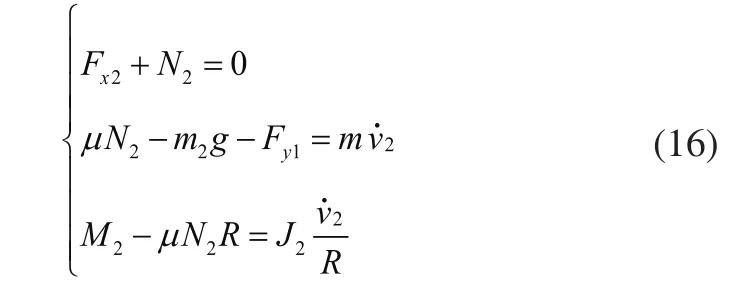
2.3 后轮越障的动力学模型

把前轮、中轮系统和机器人本体作为一个整体进行研究，对后轮和本体两部分进行动力学建模与分析。建立直角坐标系xoy，如图5所示。变量为后轮质量；分别为后轮对连杆1的作用力在水平和垂直方向的投影；Fx3、Fy3分别为连杆1对后轮的作用力在水平和垂直方向的投影。

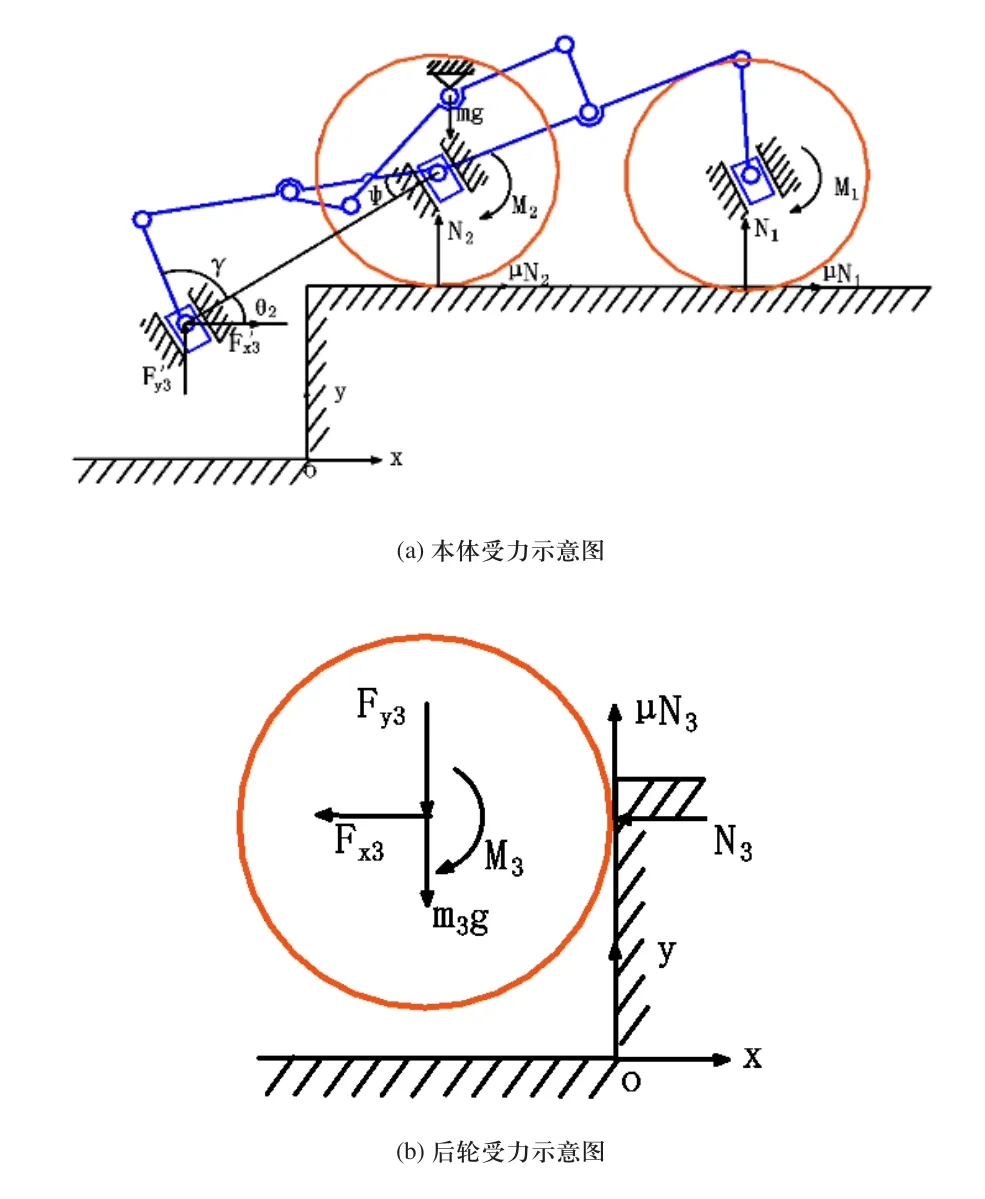
图5 后轮越障阶段机器人动力学模型

首先以机器人本体为研究对象，在后轮越障过程中，本体质心的转动惯量为J，质心到中轮中心的距离为H，位置由表示，可以得出：

已知后轮质心在垂直方向上的速度为，转动惯量为J3，建立后轮的动力学模型为：

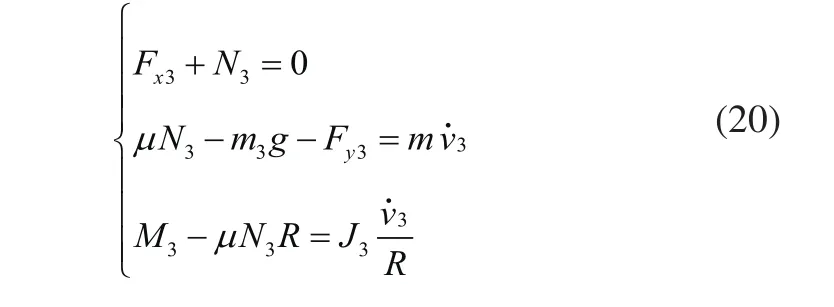
2.4 机器人动力学模型分析

机器人越障过程的动力学模型体现了机器人的运动状态、质心位置、垂直障碍高度、轮地附着系数等参数对驱动力矩的影响，电机需要给轮子提供足够的驱动力才能完成整个越障过程，这为提高机器人的越障能力提供了理论基础。

以整个越障过程为分析对象。在前轮越障阶段，前后轮的传动轴相对于本体沿滑槽向上移动，使得连杆6对中轮在垂直方向的作用力随着角度的增大而逐渐增大，角度不变，这将导致地面对中轮的支持力逐渐增大，在前轮越障阶段的初期，出现最大值，此时中轮所需的驱动力最大，这是前轮越障过程中对电机的输出力矩需求最高的极限状态；在中轮越障阶段，前后轮的传动轴相对于本体沿滑槽向下移动，使得连杆6对中轮在水平方向的作用力随着角度的减小而逐渐增大，同时连杆3对中轮在水平方向的作用力随着角度的增大而逐渐增大，二者共同导致台阶垂直面对中轮的支持力逐渐增大，在中轮越障阶段的初期，出现最大值，此时中轮所需的驱动力最大，这是中轮越障过程中对电机的输出力矩需求最高的极限状态；在后轮越障阶段，前后轮的传动轴相对于本体沿滑槽向上移动，连杆3对中轮在垂直方向的作用力随着角度的减小而逐渐增大，二者共同导致地面对中轮的支持力逐渐增大，在后轮越障阶段的初期，出现最大值，此时中轮所需的 驱动力最大，这是后轮越障过程中对电机的输出力矩需求最高的极限状态。

根据所建立的动力学模型以及动力学模型分析可以得出，机器人越过垂直障碍过程中，中轮所需要的驱动力矩始终最大，并且发生在越障的初期。

3 六轮全地形移动机器人动力学仿真

六轮全地形移动机器人的动力学仿真采用ADAMS软件作为仿真分析平台。利用ADAMS建立了动力学仿真模型，垂直障碍为150mm的楼梯台阶，在ADAMS中建立的障碍模型和虚拟样机。机器人通过垂直障碍的仿真过程，如图6所示。可以看出机器人的运动机构通过悬架的配合，能够顺利通过楼梯台阶，验证了机器人的越障能力以及结构设计的合理性。

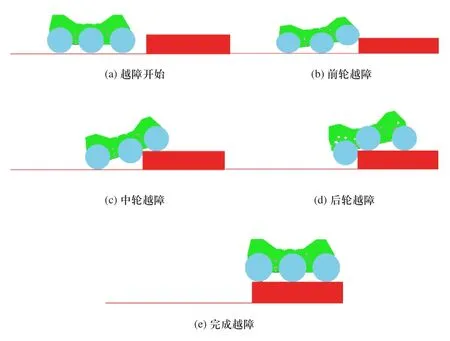
图6 机器人通过垂直障碍的仿真过程截图

经过ADAMS的后处理工具可以得出机器人各个车轮的驱动力矩曲线。前轮的驱动力矩曲线如图7所示，中轮的驱动力矩曲线如图8所示，后轮的驱动力矩曲线如图9所示。从图中可以看出，0s～6s为前轮越障阶段，越障过程为图6中(a)～(b)，此阶段中轮的峰值力矩最大为5.88N.m；6s～13s为中轮越障阶段，越障过程为图6中(c)～(d)，此阶段中轮的峰值力矩最大为6.51N.m；13s～20s为后轮越障阶段，越障过程为图6中(d)～(e)，此阶段中轮的峰值力矩最大为8.25N.m。

图7 机器人越障时前轮力矩曲线

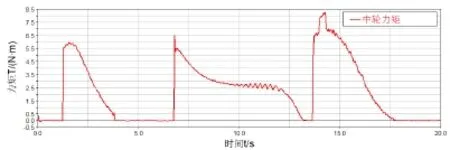
图8 机器人越障时中轮力矩曲线

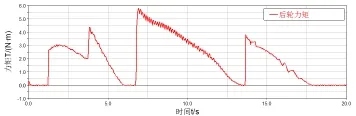
图9 机器人越障时后轮力矩曲线

通过以上的仿真分析可知整个越障过程的三个阶段始终是中轮的峰值力矩最大，与动力学模型的分析相吻合，为电机以及减速机的选型提供了理论依据。

机器人前轮、中轮、后轮的位置曲线如图10所示，从图中可以看出机器人是按照前轮、中轮、后轮的顺序依次进行越障，并且每个车轮在垂直方向的位移变化量为150mm。通过以上的仿真分析可知机器人顺利通过了高度为150mm的垂直障碍，这足以证明机器人的越障能力。

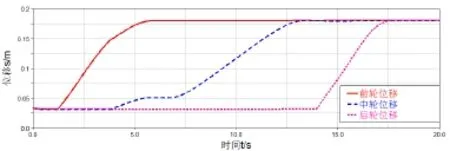
图10 机器人越障时前轮、中轮、后轮的位置变化曲线

4 越障性能实验

选择各种高度的水泥凸台搭建越障性能实验平台。根据车轮半径为100mm，实验设置的垂直障碍高度为100mm、120mm、140mm、150mm、160mm，垂直障碍的测量工具选择直尺。设置样机的行进速度为0.02m/ s，样机越障性能实验结果如表1所示，其中爬越150mm水泥凸台的越障过程如图11所示。

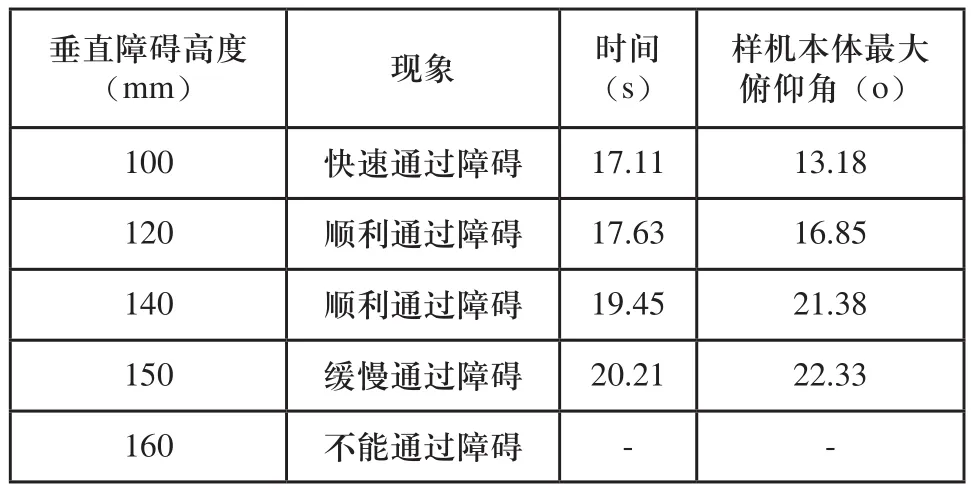
表1 样机越障性能实验结果

图11 机器人通过150mm障碍的实验过程

实验结果表明，样机能够顺利通过150mm的水泥凸台，完成时间为21s。说明该样机具有较强的越障能力。

5 结论

1）根据悬架结构特点，对六轮全地形移动机器人的越障过程进行了分析。

2）基于达朗贝尔法建立了机器人越障动力学模型并进行了分析，得出了机器人在中轮越障过程初期电机驱动力矩最大。基于ADAMS对虚拟样机爬越台阶垂直障碍进行了动力学仿真，验证了动力学模型及分析的正确性，仿真结果为电机及减速器选型提供了理论基础。

3）越障性能实验表明，基于悬架结构的六轮全地形移动机器人能够顺利越过150mm的水泥凸台障碍，移动机器人的越障性能较强。

[1] 田海波,方宗德,古玉锋.轮腿式机器人越障动力学建模与影响因素分析[J].机器人,2010,32(3):1-397.

[2] 丁良宏,王润孝,冯华山,李军.浅析BigDog四足机器人[J].中国机械工程,2012,23(5): 505-514.

[3] 李允旺.矿井救灾机器人行走机构研究[D].徐州:中国矿业大学, 2010.

[4] Wilson L,Williams C,Yance J, etc. Design and modeling of a redundant omni-directional RoboCup Goalie[A].Proceedings RoboCup 2001 International Symposium[C].Seattle:2001.

[5] Liu J G, Wang Y C,Ma S G, et al. Analysis of stairs-climbing ability for a tracked reconfigurable modular robot[A].Proceedings of the IEEE International Workshop on Safety, Security, and Rescue Robots[C].Piscataway,NJ,USA:IEEE,2005.36-41.

[6] 于涌川,原魁,邹伟.全驱动轮式机器人越障过程模型及影响因素分析[J].机器人,2008,30(1):1-6.

[7] 冯虎田,欧屹,高晓燕.小型地面移动机器人特殊运行姿态动力学建模与分析[J].南京理工大学学报（自然科学版）,2006, 30(4):486-490.

[8] 石维亮,王兴松,贾茜.基于Mecanum轮的全向移动机器人的研制[J].机械工程师,2007(9):18-21.

[9] Wilson L,Williams C,Yance J, etc.Design and modeling of a redundant omni-directional RoboCup Goalie[A].Proceedings RoboCup 2001 International Symposium[C].Seattle:2001.

[10] West M,Asada H H. Design and control of ball wheel omnidirectional vehicles[A].Proceedings of the 1995 IEEE International Conference on Robotics and Automation[C].1995. 1931-1938.

obstacle negotiation performance analysis and simulation for six wheel all-terrain mobile robot

WANG Chao-xing1, WANG Dian-jun2, CHEN Ya2, LIU Zhan-min2, XIANG Chen2

TP242.2

A

1009-0134(2016)12-0072-06

2016-08-15

北京石油化工学院URT项目（2014J00082）

王超星（1989 -），男，河南人，硕士研究生，研究方向为机器人技术。