具有非单调功能响应及阶段结构的时滞捕食与被捕食系统的概周期性
周铁军,向美红,刘迎媛
(湖南农业大学 理学院,湖南 长沙,410128)
具有非单调功能响应及阶段结构的时滞捕食与被捕食系统的概周期性
周铁军,向美红,刘迎媛
(湖南农业大学 理学院,湖南 长沙,410128)
研究一类捕食者和被捕食者都具有阶段结构,功能响应是非单调函数的时滞捕食与被捕食系统的概周期性,利用Brouwer不动点定理获得了系统存在概周期解的条件。
概周期解;捕食与被捕食;阶段结构;非单调功能响应
种群动力学中“群体防御”的现象表明,捕食者功能响应函数也可能不是关于食饵单调增加的。为了描述这种现象,Andrews提出了Holling-IV 类功能响应函数[1],这是一种非单调的函数。文献[2-4]研究了Holling-IV 类的功能响应函数捕食与被捕食系统的持久生存性、全局吸引性及周期性等问题。种群动力学研究中还有一种比较合理的研究思路是考虑种群的差异,建立阶段结构模型[5-7]。自上个世纪20年代丹麦物理学家H.Bohr 提出概周期函数的理论以来,该理论就一直被广泛应用在常微分方程、时滞微分方程等领域。目前综合考虑具有阶段结构、Holling-IV类功能反应函数的捕食与被捕食模型,其研究结果还不多见[8,9]。本文针对此类模型研究它的概周期解的存在性。
1 模型与引理
我们在[9]中提出了如下形式的捕食与被捕食者模型并研究了(1)的持久生存问题:
其中x1(t)与x2(t)分别表示幼年和成年被捕食者在时刻t的密度,y1(t)与y2(t)分别表示幼年和成年捕食者在时刻t的密度,功能反应取如下形式的Holling-IV型函数
另外假设方程(1)的初始条件为:
x1(θ)=γ(θ)≥0,x2(θ)=η(θ)≥0,y1(θ)=μ(θ)≥0,y2(θ)=ν(θ)≥0,θ∈[-τ,0].其中τ=max(τ1,τ2),γ,η,μ,ν是[-τ,0]连续的概周期函数。
关于系统(1)持久性有如下结论(文献[9]定理1):
定理A 假设
则系统(1)是持久生存的。
系统(1)具有持久生存性,说明存在正数mi,ni,Mi,Ni(i=1,2)(其计算式见文献[9])使得
其中
另外我们列出指数二分性和概周期解存在性结论如下[10]。
定义1 设x∈n,Q(t)为定义在上的矩阵,下列线性系统
x′(t)=Q(t)x(t),
(2)
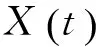
‖X(t)PX-1(s)‖≤ke-α(t-s),t≥s,
‖X(t)(I-P)X-1(s)‖≤ke-α(t-s),t≤s.
则称该系统在R上具有指数二分性。
引理1 若线性系统(2)具有指数二分性,则下列概周期系统
x′(t)=Q(t)x+g(t)
有唯一的概周期解且
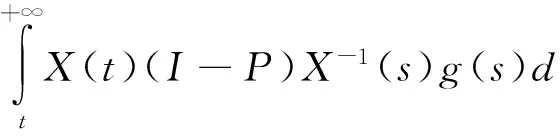
(3)
引理2 假设ci(t)是R上的概周期函数,且
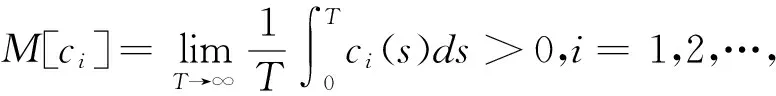
在R上具有指数二分性。
2 系统概周期解的存在性
定义B={(φ,ψ)|φ,ψ是上的概周期函数)},对于任意的(φ,ψ)∈B,如果定义范数‖(φ,ψ)‖B=supt∈max{|φ(t)|,|ψ(t)|},那么B是Banach空间。
系统(1)中第2和第4个方程不含x1(t)及y1(t),所以我们考虑它的如下子系统
该子系统初始条件满足:x2(θ)=η(θ)≥0,y2(θ)=ν(θ)≥0,θ∈[-τ,0]。

也是概周期的。
根据系统(1)再考虑如下2 个概周期线性微分方程:
(5)
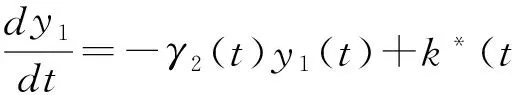
(6)
在系统(1)的初始条件下,方程(5)有唯一解
同理,方程(6) 有唯一解
若系统(1) 初始条件满足:
则从(7) 、(8) 知,方程(5) 有唯一概周期解
同理,方程(6) 有唯一概周期解
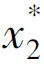
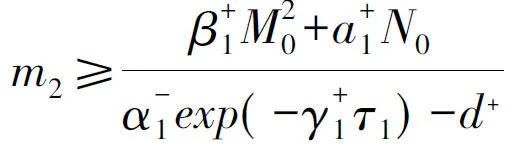
证明根据前面的分析,我们只要证明子系统( 4) 存在概周期解即可。对于任一φ= (φ,ψ)∈B 考察如下方程组
因为M[d]>0,M[β2]>0,由引理2 知下列线性微分方程组具有指数二分性,
由引理1 知系统( 11) 有一个概周期解
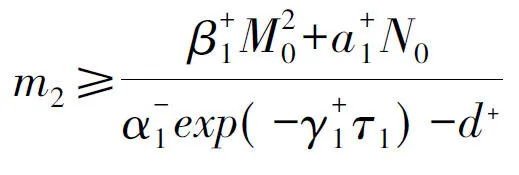
再由条件
可得
下面考虑如下系统:

则由系统(14)可得
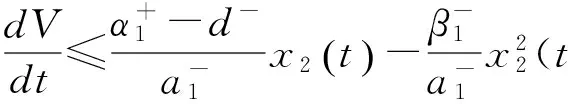
根据比较原理,可得
于是得
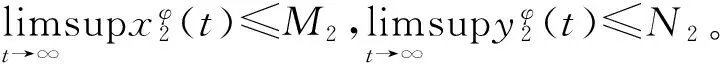
因此T是B*到B*上的连续自映射。于是,根据Brouwer不动点定理,算子T至少存在一个不支点φ∈B*,使得T(φ)=φ,从而φ=(φ,ψ)是系统(4)的一个概周期解。因此系统(1)也具有相应的正的概周期解。
3 结论
本文在系统具有持久性的条件下通过构造一个连续的自映射由Brouwer不动点定理获得了具有阶段结构的时滞捕食系统至少存在一个概周期解的条件。当然,如果能够证明该映射还是压缩映射,则可以进一步证明该系统的概周期解是唯一的,但系统较为复杂,有待以后进一步的研究。
[1]John F.Andrews.A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates[J].Biotechnology and Bioengineering,1968,10(6):707-723.
[2] W.Yang,X.Li,Z.Bai.Permanence of periodic Holling type-IV predator-prey system with stage structure for prey[J].Mathematical and Computer Modelling,2008,48:677-684.
[3] 王守和,魏凤英.具有IV类功能反应和无穷时滞的捕食系统的持久性和全局吸引性[J],吉林师范大学学报(自然科学版),2009,2:63-66,72.
[4] Y.Xue,X.Duan.The dynamic complexity of a Holling type-IV predator-prey system with stage structure and double delays[J].Discrete Dynamics in Nature and Society,2011,(5):642-663.
[5] P.Georgescu,Y.Hsieh.Global dynamics of a predator-prey model with stage structure for the predator[J].SIAM Journal on Applied Mathematics,2007,67(5):1379-1395.
[6] Meng Xinzhu,Jiao Jianjun,Chen Lansun.The dynamics of an age structured predator-prey model with disturbing pulse and time delays[J].Nonlinear Analysis Real World Applications,2008,9(2):547-561.
[7] C.Liu,Q.Zhang,Y.Zhang,et al.Bifurcation and control in a differential-algebraic harvested prey-predator model with stage structure for predator[J].International Journal of Bifurcation and Chaos,2008,18(10):3159-3168.
[8] Y,Liu,X.Zhang,T.Zhou.Multiple periodic solutions of a delayed predator-prey model with non-monotonic functional response and stage structure[J],Journal of Biological Dynamics,2014,8(1):145-160.
[9] 刘迎媛,周铁军.具有阶段结构的时滞捕食与被捕食系统的持久性[J].湖南文理学院学报(自然科学版),2015,27(2):10-13.
[10] 何崇佑.概周期微分方程[M].北京:高等教育出版社,1992.
Almost periodicity of a delayed predator-prey system with stage structure and non-monotonous functional response
ZHOU Tiejun,XIANG Meihong,LIU Yingyuan
(College of Science,Hunan Agricultural University,Changsha 410128,China)
The almost periodicity of a delayed predator-prey system with stage structure for both predator and prey,and with non-monotonous functional response is studied.Based on Brouwer fixed point Theorem,some sufficient conditions are obtained for the existence of an almost periodic solution of the system.
almost periodicity;predator-prey;stage structure;non-monotonous functional response
1672-7010(2016)04-0005-06
2016-09-20
湖南省科技计划项目(2015JC3101);湖南省研究生创新培养专项(CX2015B265)
周铁军(1965-),男,湖南汨罗人,教授,博士,博士生导师,主要从事生物数学的研究
O175.1
A

