基于剩余寿命的可变成本实时预测维护技术
陈 静, 吴 锐
(安徽工业经济职业技术学院, 合肥 230051)
基于剩余寿命的可变成本实时预测维护技术
陈 静, 吴 锐
(安徽工业经济职业技术学院, 合肥 230051)
针对设备可变成本的实时预测维护,给出了同时考虑长期运行成本期望与方差的最优维护策略,通过定义成本方差敏感因子以及调节方差成本敏感因子的大小,从而实现维护成本、维护次数和失效风险之间的动态平衡。将提出的维护策略应用到设备维护当中,实例分析表明相对于期望成本维护策略,可变成本维护策略决策结果保守,不确定性小,能够有效减少管理与失效的风险。
寿命预测;预测维护;期望;方差
引 言
目前,预测维护越来越受到各国研究人员的普遍关注[1-4],而现有的预测维护成本函数模型都只考虑单位时间期望维护成本[5-7]。在预测维护模型中,剩余寿命是一个随机变量,因此维护决策中的维护成本函数也是随机的。这一随机变量的数学期望,不能反映维护成本函数的不确定性特征。维护成本函数的不确定性可以用其自身的方差进行表征,同时考虑维护成本函数的期望与方差,有助于制定更加合理的维护策略。现有的考虑维护成本方差的研究[8-10]假设设备的寿命分布已知,且只针对一类设备安排维护操作。对于单个设备,没有利用实时运行监测数据。在工程实践当中,应当充分考虑寿命分布随设备运行状态的变化,实时更新最优维护时间,以保证更新维护时间能够精确反映被监测设备当前时刻的实际运行状态。据调查,各类企业在维修中的投入占生产总成本的15%~70%[11]。维修活动安排及维修资源管理的不当,将会影响整个生产过程并造成浪费。因此,在系统运行过程中,根据监测信息及时发现异常或定量评价系统健康状态并采取有效维修措施,对于切实保障复杂系统的运行安全性、可靠性与经济性具有重要意义[12-15]。
因此,在预测维护的框架下,如何综合考虑维护成本的期望和方差,降低管理风险,减少失效事件的发生是一个亟待解决的问题。本文基于可变成本的实时预测维护技术,给出了同时考虑长期运行成本期望与方差的最优维护策略。
1 基于剩余寿命的最优维护策略
1.1 模型基本假设
根据工程实践,对预测维护模型作出如下基本假设:
(1)对于单个设备,设随机变量X(t)表示t时刻的系统退化状态(X(t)=0表示设备处于全新状态),随着时间的推移,设备性能会逐渐退化,当X(t)≥l(l为失效阈值)时认为设备发生失效。
(2)检测是非破坏性的,且能够完全反映系统退化程度,即只有通过性能检测才能判定设备是否失效,检测时间可以忽略。
(3)当前时刻设备的性能检测结果仅依赖于当前时刻设备的状态。
(4)忽略测试对设备性能、寿命分布的影响。
(5)在检测到设备发生失效前,其剩余寿命分布不发生改变。
1.2 基于长期运行期望成本最小的维护策略
该维护策略详细描述如下:
(1)对性能退化设备进行周期性检测。
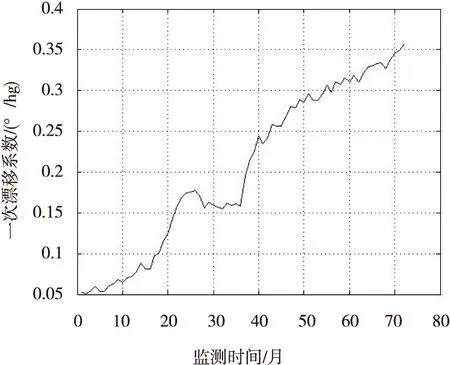
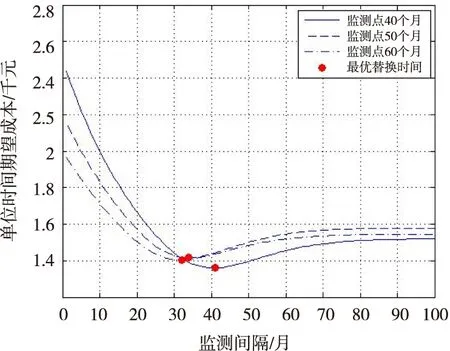
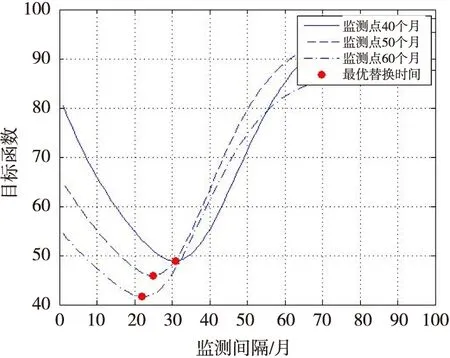
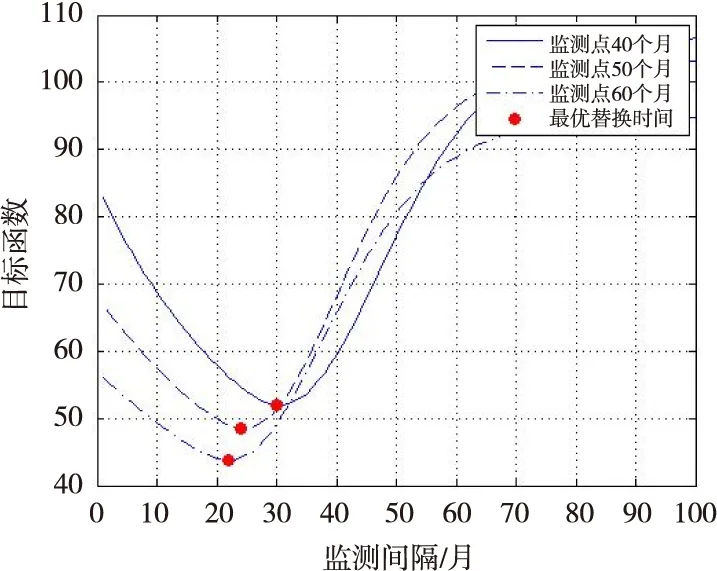
(2)主要考虑两种维护操作:预防性替换和失效时替换。预防性替换引起的损失记为Cp,工程实践中认为一般小于失效时替换所引起的损失Cf,0 (3)假设设备运行至ti时刻,需要确定最优预防性替换时刻tr,确定的依据就是设备单位时间长期运行的平均费用最小。参考文献[10],给出平均费用模型: (1) 式中:φπ(t)表示单位时间长期运行期望成本;C(t)为期望费用;T(t)为平均寿命。 (2) (3) 将式(2)式和(3)式代入(1)式就可以得到单位时间长期运行期望成本 φπ(t)= (4) 1.3 同时考虑长期运行成本期望与方差的最优维护策略 1.3.1 长期运行成本方差 (5) 长期运行期望均方成本ψπ(t)可表示为: (6) 长期运行成本方差Vπ(t)可定义为: (7) 维护决策问题可以转化为更新过程,有如下的定理成立。 定理1 在维护策略π下,长期运行成本方差可表示为: (8) 证明 根据式(5)、式(6)和式(7),有 (9) 定理得证。 1.3.2 预测维护决策目标函数 当前监测时刻ti,得到设备退化状态的历史监测数据和当前监测信息X1:i={X1,X2,…,Xi}和剩余寿命分布的概率密度函数fLi|X1:i(li|X1:i)和累积分布函数FLi|X1:i(li|X1:i),则长期运行单位时间期望成本为标准的决策目标函数如式(4)所示。综合考虑两者,定义长期运行期望均方成本: ψπ(tr)= (10) 式(4)同式(10)都刻画了长期运行维护成本的平均水平,即均值。根据引理1,预测维护框架下,定义长期运行成本方差为: Vπ(t)=ψπ(t)-(φπ(t))2 (11) 式(11)刻画了实际运行成本相对于均值的离散程度。则基于可变成本的预测维护问题可定义为: (12) 其中:α为成本方差敏感因子。由于φπ(t)>0,最小化(φπ(t))2等价于最小化φπ(t)。因此,当α=0时,目标函数即式(12)等价于传统的以期望成本为决策目标函数的维护策略。 式(12)中α表示成本方差的相对权重。α≤1意味着决策者认为改进成本方差对最终决策的影响小于改进期望成本所产生的影响,即期望成本比成本方差重要。类似地,α≥1意味着决策者认为成本方差比期望成本重要。但是,根据工程实际情况,一般认为0≤α≤1是合理的。 2.1 问题描述 应用实例中选取某型号陀螺仪为预测维护对象,陀螺仪漂移是表征惯导系统的一项重要指标,可以看作惯导系统的一种缓变失效。为了确保陀螺仪能正常工作,需要对陀螺仪进行定期监测,出厂后通常为每月检测一次,对测得的数据进行记录,并进行研究分析。图1为某型陀螺仪的一次项漂移系数72组月监测数据,表1给出了模型的维护阈值和维护成本。 图1 陀螺仪一次项漂移系数月监测数据 参数失效阈/(°/hg)成本/千元lCmCpCf数值0.5160100 2.2 基于退化模型的陀螺仪最优维护时间确定 以长期运行单位时间期望成本为标准,其目标函数为式(4),决策结果如图2所示。 图2 仅考虑单位时间期望成本决策结果 如果将长期运行单位时间成本方差也考虑进去,分别令成本方差敏感因子α=0.02,α=0.3和α=0.9,其目标函数为式(12),其决策结果如图3~图5所示。 图3 可变成本策略(α=0.02) 图4 可变成本策略(α=0.3) 图5 可变成本策略(α=0.9) 由图3~图5可知,在不同的检测时刻,基于可变成本的维护策略的最优替换时间都小于期望成本维护策略的最优替换时间。直观上可以看出,随着成本方差敏感因子α的逐渐增大,最优替换时间有变小趋势。由式(12)可以知道,成本方差敏感因子α代表的是成本方差因素对决策目标函数的影响,α越大,方差成本对决策结果影响越大,α越小,期望成本对决策结果影响越大。为了便于对比分析,同时给出只考虑长期运行单位时间方差成本(目标函数为Vπ(t))的决策结果如图6所示。 图6 仅考虑单位时间方差成本决策结果 对比图2~图6可以发现,随着成本方差敏感因子α从0向1逐渐增大,最优替换时间也从仅考虑单位时间期望成本决策结果向仅考虑单位时间方差成本决策结果过渡。为了定量地进行对比分析,表2列出了不同维护策略下最优替换时间和对应的最小成本。 表2 不同维护策略的维护成本与最优替换时间 由表2可知,在基于可变成本的预测维护策略下,最优替换时间间隔比基于长期运行期望成本的决策结果要短,即基于可变成本的预测维护的决策结果相对于传统方法的决策结果保守。随着成本方差敏感因子α从0向1逐渐增大,最终决策结果趋近于长期运行方差成本最小的维护策略的决策结果,直观上与实际情况相符合,即通过增加替换的频率来降低陀螺仪失效的风险。基于长期运行单位时间期望成本最小的维护策略,替换时间间隔最长,维护成本最低,但是是以牺牲陀螺仪失效的代价为前提,即陀螺仪失效风险较大;基于长期运行单位时间方差成本最小的维护策略,陀螺仪相对可靠性较高,即失效风险效低,但是维护次数频繁,且维护成本较高。为了便于清楚观察这一结果,图7给出了监测点40个月、50个月和60个月的可靠度曲线,可以看出,随着时间的增加,可靠性曲线逐渐左移,即可靠性较低。表3分别列出了不同维护策略下的最优替换时间和对应的可靠度,验证了上述分析结果。 图7 不同监测点可靠度曲线 监测点40月50月60月最优替换时间(期望成本最小)81月84月92月可靠度0.78460.80600.8044最优替换时间(方差成本最小)70月74月82月可靠度0.97780.98360.9832 本文基于可变成本的维护策略,同时考虑了长期运行单位时间成本期望和方差,通过调节方差成本敏感因子α的大小,从而实现维护成本、维护次数和失效风险之间的动态平衡。针对具体设备和维护预算,方差成本敏感因子α的大小可以通过专家经验和工程实践进行确定。在预测维护框架下,最优替换时间可以随着剩余寿命分布的更新而动态更新,从而实现对设备的最优维护。 [1] 周东华,魏慕恒,司小胜.工业过程异常检测、寿命预测与维修决策的研究进展[J].自动化学报,2013,39(6):711-722. [2] ZHOU Z J,HU C H,XU D L,et al.A model for real-time failure prognosis based on hidden Markov model and belief rule base[J].European Journal of Operational Research,2010,207(1):269-283. [3] SI X S,WANG W,HU C H,et al.Remaining useful life estimation—A review on the statistical data driven approaches[J].European Journal of Operational Research,2011,213(1):1-14. [4] 康建设,尹健.装备故障诊断、预测与信息管理[J].仪器仪表学报,2006,27(6):1752-1757. [5] WANG W.A two-stage prognosis model in condition based maintenance[J].European Journal of Operational Research,2007,182(3):1177-1187. [6] CARR M J,WANG W.An approximate algorithm for prognostic modeling using condition monitoring information[J].European Journal of Operational Research,2011,211(1):90-96. [7] KAISER K A,GEBRAEEL N Z.Predictive maintenance management using sensor-based degradation models[J].IEEE Transactions on Systems,man and Cybernetics,Part A:Systems and Humans,2009,39(4):840-849. [8] CHEN Y,JIN J H.Cost-variability-sensitive preventive maintenance considering management risk[J].IIE Transactions,2003,35(12):1091-1101. [9] GIRI B C,DOHI T.Quantifying the risk in age and block replacement policies[J].Journal of the Operational Research Society,2010,61:1151-1158. [10] TONG D J.Hierarchical variance decomposition of system reliability estimates with duplicated components[J].IEEE Transactions on Reliability,2008,57(4):564-573. [11] 王浩伟,徐廷学,王波.基于Wiener 模型的某型导弹电连接器寿命预测[J].战术导弹技术,2014(1):42-45. [12] 周东华,陈茂银,徐正国.可靠性预测与最优维护技术[M].合肥:中国科学技术大学出版社,2013. [13] ASME.ASME boiler & pressure vessel code,VIII Division 2,alternative rules for construction of pressure vessels[S]. [14] BARKER C T,NEWBY M J.Optimal non-periodic inspection for a multivariate degradation model[J].Reliability Engineering and System Safety,2014,94(1):33-43. [15] 王璐,王正,宋希庚,等.疲劳短裂纹理论及寿命预测方法新进展[J].机械强度,2012(4):597-603. Variable Costs Real-time Predictive Maintenance Technology Based on Remaining Life CHENJing,WURui (Anhui Technical College of Industry and Economy, Hefei 230051, China) Considering the real-time predictive maintenance for equipment variable costs, the optimal maintenance strategy taking into account the expectation and variance of long-term operating costs is proposed. Firstly, the basic assumptions of maintenance model are given. Secondly, the desired minimum running costs based on long-term maintenance strategy are also given by defining the cost variance sensitive factor and considering the long run time unit cost expectation and variance for the decision. By adjusting the variance cost sensitivity factor, the dynamic balance between maintenance cost, maintenance time and failure risk is realized. Finally, the proposed strategy is applied to equipment maintenance. Example analysis shows that, variable cost maintenance strategy can effectively reduce the risk of the management and failure with conservative results and small uncertainty with respect to the expected cost maintenance strategy. life prediction; predictive maintenance; expectations; variance 2016-06-20 安徽省质量工程项目(2015ckjh135) 陈 静(1982-),女,安徽合肥人,讲师,工程硕士,主要从事数据库、电子商务方面的研究,(E-mail)orangejj@126.com 1673-1549(2016)06-0085-05 10.11863/j.suse.2016.06.17 V241.5 A
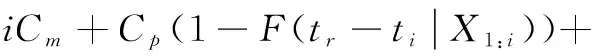
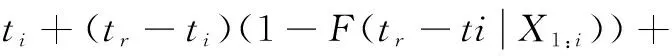
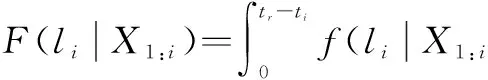

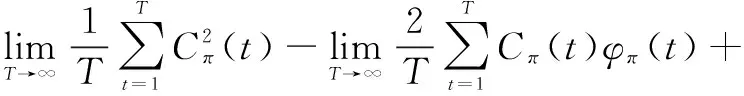
2 应用实例






3 结束语

