基于改进K-Means算法的保险客户细分研究

张君韬，何丽

（天津财经大学理工学院，天津 300222）

基于改进K-Means算法的保险客户细分研究

张君韬，何丽

（天津财经大学理工学院，天津 300222）

通过聚类实现客户细分，能够从客户的人口统计信息和历史消费行为中发现客户的购买偏好和购买行为,这将为保险行业的营销决策制定提供重要依据。针对传统K-Means算法对于客户细分初始条件敏感的弱点，提出基于黄金分割的改进K-Means聚类方法，该方法能够确定最佳聚类个数，并通过实例验证该算法在保险客户细分中的有效性。

客户细分；保险；K-Means聚类；数据挖掘；主成分

0 引言

客户细分最早由美国著名的市场学家温德尔·史密斯（Wendell R·Smith）提出，指企业按照客户属性将客户群体分为若干个子客户群体，并实现细分后不同客户群体之间的差异最大化，每个客户群体尽可能的相似。随着保险市场竞争的日趋激烈，各保险企业汇集了大量客户信息和业务数据，这些数据背后隐藏客户的行为偏好和消费潜力。应用数据挖掘中的聚类方法可以有效地实现保险客户的细分，从而发现不同客户群的行为偏好和未来的购买偏好。

本文针对保险行业客户数据的特征和客户分析目标，提出了基于主成分分析和改进K-Means算的客户细分模型，并使用荷兰数据挖掘公司Sentient Machine Research为the COIL CHALLENGE 2000大赛提供的保险客户数据对提出的模型的有效性进行了验证。

1 细分变量提取

细分变量选择是建立客户细分模型首先要解决的问题。考虑到保险客户数据一般包含很多属性，且不同的属性之间存在一定的相关性，本文将客户细分变量的提取分成两个主要阶段：数据预处理阶段和主成分分析阶段。

1.1 数据预处理

数据挖掘中数据预处理的主要任务是对目标数据集中的数据进行清洗、过滤和数据格式转换等。保险客户数据库通常是由保险企业多个不同险种数据库整合而来的，存在客户信息的不完整和属性值取值范围不一致性等情况。为了实现客户细分结果的准确有效，需要对客户数据库中的相关属性进行数据清洗和数据转换等。其中，数据清洗过程完成对缺省值、无效值和未知值的处理；数据转换完成数据泛化过程。所谓泛化处理就是用更高层次的概念来取代低层次的对象。

1.2 主成分分析

经过预处理后的客户属性少则几十个，多则上百个，而且这些变量之间可能会存在较强的相关性而产生冗余。主成分分析是一种对高维数据进行降维处理的一种分析方法。通过主成分提取，不仅可以消除相关性变量所产生的信息冗余，还可以有效降低客户细分聚类模型的输入维度。主成分在代数学上是p个随机变量X1，X2，…，Xp，的一些特殊的线性组合，每个线性组合利用原数据变量生成新变量，即主成分。设随机向量X=[X1，X2，…，Xp]，考虑随机向量的线性组合如公式（1）。

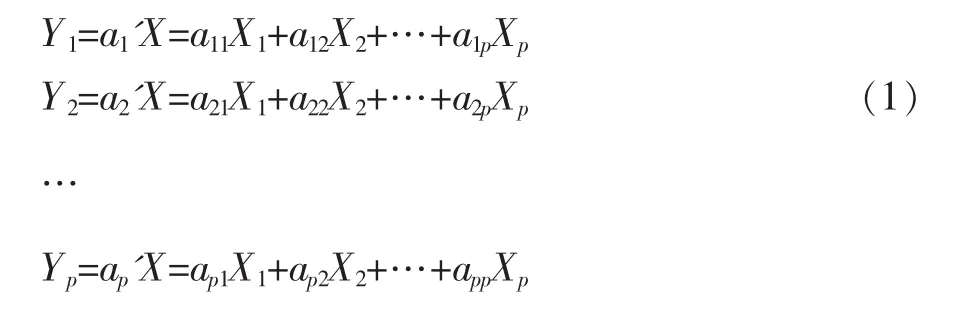
主成分是Y1，Y2，…，Yp中方差尽可能大的那些不相关的线性组合。Y1表示第一主成分，即Var（Y1）最大。一个变量的方差越大，表示其包含的信息越多。为了不丢失原始随机变量中的有价值信息，一般需要选择k个主成分（k≥2）。为了保证任意两个主成分之间不存在信息重合，主成分Yi，Yj,之间的协方差需要满足Cov（Yi，Yj）=0，1≤i，j≤k且≠j。

本文通过主成分分析法来提取客户数据集中的主成分变量和与任何变量都不相关的变量作为客户细分模型的输入变量。

2 基于改进K-Means算法的客户细分模型

聚类分析是一种实用的多元统计分析方法，它将一批样本按照它们在性质上的亲疏、相似程度进行分类。分类的目标是使同一类中的样本之间具有较大的相似性，不同类样本之间的相似性尽可能小。K-Means聚类，也称为动态聚类算法，是客户细分中最常用的聚类算法之一。在传统的K-Means聚类算法描述中，初始聚类个数k的取值和初始聚类中心的选择将直接影响K-Means的聚类结果，并且K-Means的聚类结果也无法反映最优聚类个数。本文借鉴“黄金分割”思想，在传统K-Means算法中引入评价指标validty（k），并通过该评价指标来确定K-Means的最佳聚类个数。validty（k）评价指标定义如公式（2）：

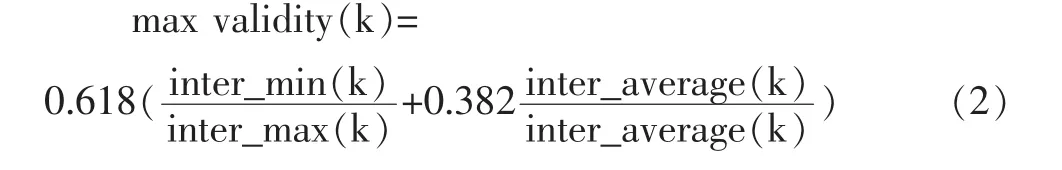
（1）确定最小、最大聚类个数k1，k2；

（2）从k1到k2进行迭代，对每次迭代的k（k1≤k≤k2）：

①利用传统K-Means聚类算法算法产生聚类结果（k，U）；

②计算聚类有效性的指标函数validty（k）；

（3）从中选取kopt使得聚类有效函数validty（k）达到最大；

（4）输出最优聚类结果（kopt，Uopt）；

（5）终止。

3 模型验证

本文实证数据来源于荷兰数据挖掘公司Sentient Machine Research为the COIL CHALLENGE 2000大赛提供的数据，共有5822条纪录，每条记录拥有86个属性，其中载有社会人口信息（属性1-43）和客户行为与产品信息（属性44-86）。社会人口信息来自邮政编码，同一地区的客户具有相同的社会人口属性。

3.1 细分变量选择

经过检查本数据集存在大量缺失值，但没有未知值和无效值。为了简化处理流程，本文对数据集中的缺失值全部用0代替。为了完成细分过程，还需要对年龄和客户主要类型这两个属性进行泛化处理。10个主要客户类型：Successful Hedonists，Driven Growers，Average Family，Career Loners等分别用数值1，2，…,10替代；对于年龄属性，将其泛化成6个不同的区间：20-30 years，30-40 years，40-50 years，50-60 years，60-70 years，70-80 years，区间取值分别为1，2，3，4，5，6。

为了在不丢失信息的前提下降低客户细分模型的输入维度，在数据集的属性结合应用主成分分析，并对相关性较高的属性提取主成分，这些主成分和与任何属性都不相关的属性一起作为细分模型的输入变量。

本文调用SAS Proc Corr过程对数据集中86个属性的相关性进行分析,其中Number of fire policies与Contribution of fire policies的偏相关系数为0.86554，P〈0.05，说明二者有显著相关性，Contribution of car policies与Number of car policies的偏相关系数为0.91615，P〈0.0001，说明二者也具有显著相关性，由此得出保险客户各险种缴纳的保费与各险种的购买数量显著相关。数据集中属性44-64是与保费相关的属性，属性65-85是与保险数量相关的属性，为消除相关带来的冗余,本文选取属性44-64进行主成分分析。根据属性之间的相关性分析结果，最终筛选出：Customer Subtype,Number of houses、Avg age、Living together、Singles等32个属性进行主成分分析。

为了进一步消除相关变量带来的信息冗余，接下来应用SAS的Proc Princomp过程对这32个属性进行主成分分析，其中特征值大于0.93的主成分共有17个，这17个主成分分别是：Customer Subtype、Number of houses、Avg age、Medium level education、Home owners、1 car、Average income、Contribution private third party insurance、Contributioncarpolicies、Contribution moped policies、Contribution life insurances、Contribution familyaccidentsinsurancepolicies、Contributionfire policies、Contribution boat policies、Contribution property insurance policies、Contribution social security insurance policies和Number of mobile home policies。这17个属性将作为客户细分模型的最终输入变量。

3.3 模型验证

为了验证客户细分模型的稳定性，本文从5822条数据里，选择2500条作为测试集，并分成两个测试组。

第一组：首先把5822条数据分成15个类，再根据这15个类各自的类中心作为测试集进行聚类分析的初始聚类中心，然后调用SAS的PROC Fastclus过程，并把Replace设置成NONE，进行分组。

第二组：直接对测试集2500条记录进行聚类分析，分成15组。

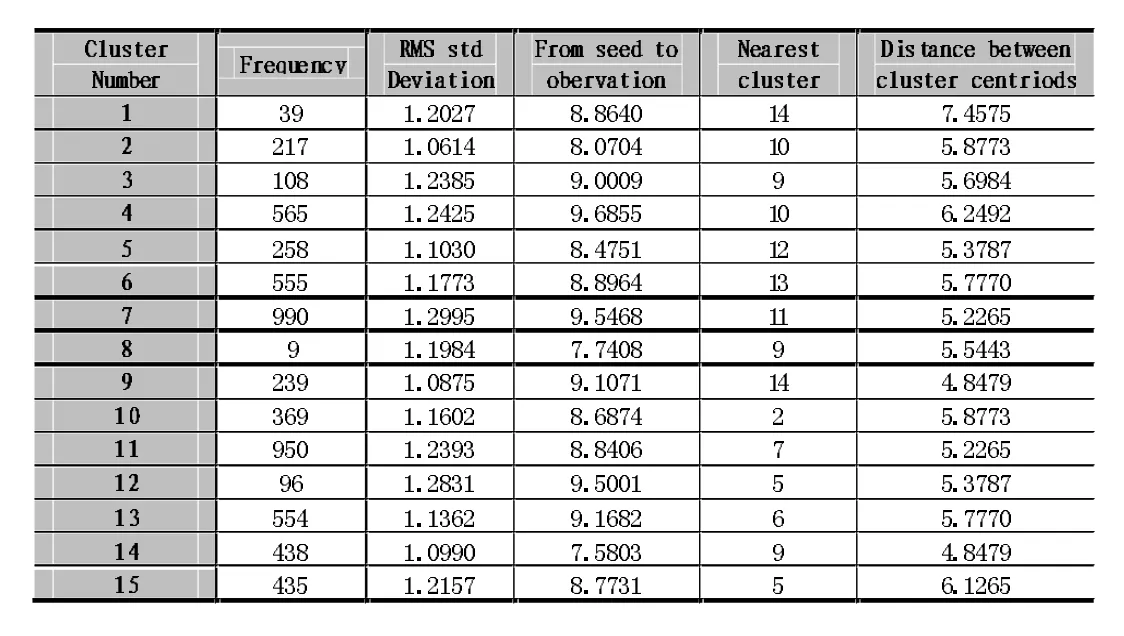
表1 客户细分结果

将测试集上两次分组的结果与上述聚类的结果进行比较发现：三次聚类的客户比例基本相同，测试第一组的类中心和原始组相同，第二组类中心点与原始组也大致相同。表2中给出了customer subtype属性在两次聚类中各组的平均值。从该结果可以看出，两组的聚类中心基本接近，说明聚类结果基本可以接受。

3.2 细分结果

4 结语

本文使用SAS的PROC Fastclus过程实现了KMeans聚类。考虑到样本数据的聚类数一般比较接近聚类输入变量的个数。为了获得最佳聚类个数，选择k从2到17，并对每个k值运行5次，计算每次聚类结果的max validity（k），然后计算每个k值对应的max validity（k）平均值。根据max validity（k）平均值越大越好的原则，最终选择初始聚类数k=15。最后获得的客户分布如表1所示。

通过主成分分析方法可以有效消除客户不同属性之间的相关性，改善K-Means聚类结果的正确性和运行效率。引入validty（k）的K-Means聚类方法克服了传统K-Means算法需要预先指定聚类数的弱点，能够客观地确定K-Means算法的最佳聚类个数。用改进的K-Means聚类分析模型对保险客户进行细分研究,能够获得正确的客户分布。根据客户细分的结果及其特征，保险企业可以针对不同的客户群设计不同的营销计划,捆绑多种不同的保险业务,以增加客户对企业产品的拥有率，争取更多有价值的潜在客户。

表2 各簇中心点customer subtype的值

[1]宋加升,陈琰.改进的K-Means聚类算法在保险客户信用分析中的算法实现.哈尔滨理工大学学报[J]，2009（2）：12-13.

[2]马子斌，杨鸿宾.客户细分在电信营销中的应用研究[J].计算机系统应用，2009（3）：105-108.

[3]赵珩君.客观聚类在客户价值细分中的研究.情报杂志[J]，2009，28（3）:151-153.

[4]范英,张忠健,凌君邀.聚类方法在通信行业客户细分中的应用[J].计算机工程，2004（12）：440-441.

[5]KE WANG,SENQIANG ZHOU.Mining Customer Value:From Association Rules to Direct Marketing[J].Data Mining and Knowledge Discovery，2005（11）,57-79.D

Research on the Insurance Customer Segmentation Based on Improved K-Means Algorithm

ZHANG Jun-tao，HE Li

（School of Science and Technology,Tianjin University of Finance and Economics,Tianjin 300222）

Customer segmentation by clustering can discover customer purchase preferences and potential buying behaviors from demographic information and the history of consuming behaviors,and these will be the important basis for insurance companies to make decisions.Considering the traditional K-Means algorithm is sensitive to initial conditions for the customer segmentation,proposes an improved K-Means clustering method based on golden section which can determine the optimum number of clusters.Empirical analysis proves that this algorithm is effective in insurance customer segmentation.

Customer Segmentation;Insurance;K-Means Clustering;Data Mining;Principal Components

2015年地方高校国家级大学生创新创业训练计划项目

1007-1423（2016）33-0014-04

10.3969/j.issn.1007-1423.2016.33.003

张君韬（1995-），男，北京人，本科，研究方向为数据挖掘

2016-09-20

2016-10-20

何丽（1969-），女，博士，教授，研究方向为数据挖掘、云计算