改进的蚁群算法与网络QoS组播路由研究

王文国，樊丽娟，刘 洋

（曲阜师范大学 信息科学与工程学院，山东 日照 276826）

改进的蚁群算法与网络QoS组播路由研究

王文国，樊丽娟，刘 洋

（曲阜师范大学 信息科学与工程学院，山东 日照 276826）

组播路由和网络服务质量（QoS），是当前Internet研究的两个重要应用课题。QoS组播路由是寻找满足特定QoS约束的一棵最优组播树，是一个典型的NPC完全多目标优化问题。针对传统蚁群算法，首次引入“蚁王”概念，使其能对路径寻优过程进行存储、排序和指导，从而使群体搜索过程更加协调有序。蚁群信息素的变化则采用精英信息素矩阵更新策略，以加快算法的收敛速度。相关仿真实验证明，这种改进的算法在解决QoS组播问题时，能够获得比基本蚁群算法明显优越的收敛性能。

蚁群算法；QoS组播路由；精英信息素；蚁王

0 引 言

蚁群算法（Ant Colony Optimization，ACO）是通过蚂蚁个体在候选解的空间中独立搜索解，并在搜寻的解上留下一定量的信息素；蚂蚁间以信息素为媒介进行间接、异步的信息传递。随着算法的推进，较优解路径上的信息素浓度会不断增加，同时其他路径上信息素浓度随着时间逐渐变弱；当算法趋于收敛时，在最优解路径上的信息素浓度最大。整个蚁群算法的最优解路径，在蚂蚁个体的共同协作下求得。意大利学者Dorigo等人通过模拟蚂蚁寻路觅食的群体行为提出了蚁群算法[1]，具有正反馈、分布式计算和贪婪启发式搜索的特点，广泛用于求解复杂的组合优化等问题[2-4]。近年来，也一些学者对该算法提出了若干优化方案[5-8]，并在不同应用领域进行了有益探索。

1 基本蚁群算法

1.1 路径选择公式

假设有m只蚂蚁放入到n个随机选择的需求节点中，每只蚂蚁根据路径上信息素的浓度选择下一个未访问的节点；每完成一步或者一个循环后，将更新调整所有路径上的信息浓度。设dij是节点i到节点j的距离；ηij是边(i,j)的能见度，ηij=1/dij，反映由节点i转移到节点j的启发程度；τij是路径(i,j)上的信息素轨迹强度；是蚂蚁k在路径(i,j)上留下的单位长度轨迹信息素量；pijk是蚂蚁k从节点i转移到节点j的状态转移概率；j是未访问的节点。

蚂蚁k在t时刻由节点i选择节点j的状态转移概率为

式中，allowedk={0,1,…,n-1}表示蚂蚁k下一步允许选择的路线。α和β为两个参数，分别反映蚂蚁在运动过程中积累的信息和启发信息在蚂蚁选择路径中的相对重要性。同时，为每只蚂蚁设计一个禁忌表tabuk(k=1,2,…,m)，记录t时刻蚂蚁k已走过的节点，禁止蚂蚁在本次循环中重复经过。循环结束后，清空禁忌表。

1.2 信息素更新

所有蚂蚁完成一次循环后，根据各蚂蚁遍历的适应度值，计算信息素增量，更新路径上的信息素。更新规则如下：

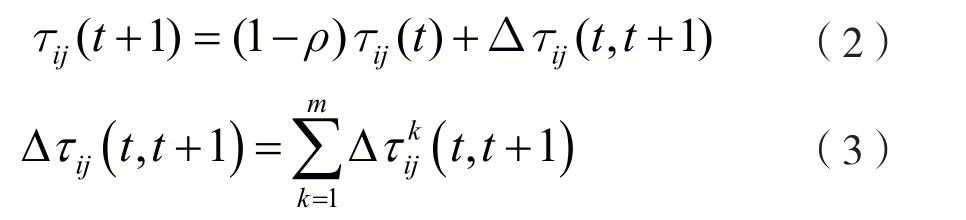
式中，ρ为信息素轨迹衰减系数，Δτijk(t,t+1)表示第k只蚂蚁在(t,t+1)时刻留在(i,j)路径上的信息素量，表示路径(i,j)的信息素增量。

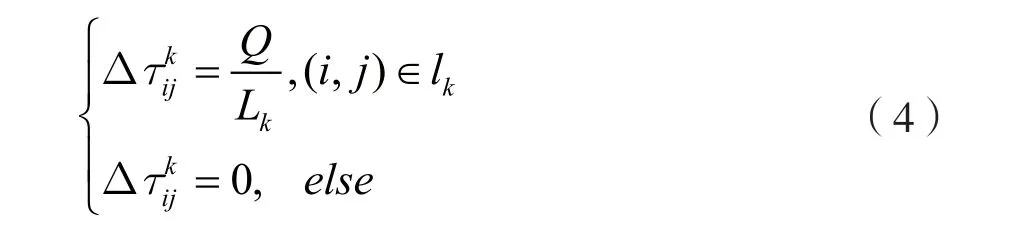
其中，Q表示初始信息素，为常量，其值由实验确定；Lk表示第k只蚂蚁在本次循环中所走路线的费用值（可以表示为长度）。

2 引入蚁王概念的改进蚁群算法

在构造解的过程中，蚁群算法因为采用随机选择策略使得算法的进化速度变慢，而正反馈原理旨在强化性能较好的解，因此失去了随机性，大量蚂蚁会选择同一条路径，从而使搜索到的路径失去了多样性，此时算法容易出现停滞现象并陷入局部最优解。

为了对传统蚁群算法进行改进，在蚁群中引入“蚁王”（或叫蚁后）概念。假设蚁王能够保存搜索到的所有候选解，并对路径进行比较排序，进而迅速发现全局最优解。目的是对群体搜索过程有整体记忆并加以指导，从而提高全局搜索效率。

2.1 算法思想

引入蚁王的蚁群算法要实现的目标是，假设不同的蚂蚁从起点出发，分别经过若干条不同路径最后到达终点，尽量让蚂蚁在初始阶段选择较多的不同路径，以获得最终的多样化解。每一只蚂蚁完成了自己的行程后，就将信息素传递给蚁王（全局信息）。每次迭代完成后，蚁王将收集到的路径按从小到大的顺序排列，并将较大路径舍弃，保存较小路径，以供蚁群下一次寻优时加以利用。每次迭代完成后，对前一轮全局最优解进一步优化，动态更新路径信息。如此反复比较，找到最短路径，然后使用信息素全局更新规则对蚂蚁所选各路径上的信息素进行更新，即蚂蚁完成一个循环后更新所有路径上的信息素，只有那些属于最短路径的边信息素才被增强，最终形成一个新的最短路径。

蚁群算法的任务就是引导问题的解向着全局最优方向不断进化。蚁王的引进能够对最优解进行快速增强，同时对最差解进行削弱，使属于最优路径的边与属于最差路径的边之间的信息量差异进一步增大，逼使蚂蚁的搜索行为更集中于最优解附近。

假设蚁王能够保存搜索到的最优值。蚂蚁将在接下来的路径选择中，根据蚁王的指导决定路径的选择，从而缓解蚁群算法的停滞现象及局部最优问题。具体的算法流程，如图1所示。

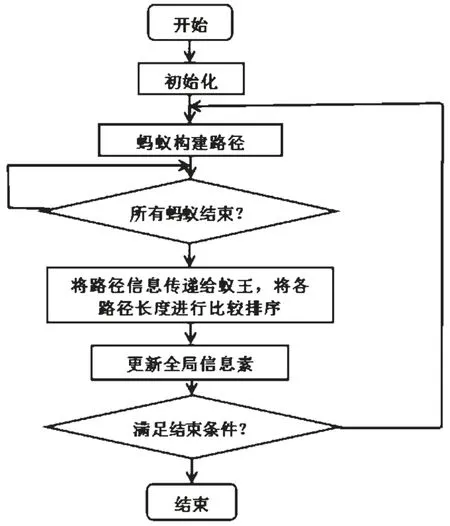
图1 改进的蚁群算法流程

3 改进的蚁群算法

3.1 蚁群的路径选择规则

蚁王可存储搜索到当前为止前g个较优解。改进蚁群算法将设置一个精英解信息素矩阵。设蚁群中有m(t)个蚂蚁按照精英信息素矩阵选择转移节点，n(t)个蚂蚁按照基本蚁群算法中边上的信息素进行选择转移节点，w(t)个蚂蚁将随机选取蚁群存储的g个较优解中的一个解，进行变异操作。

设精英信息素矩阵时刻t边(i,j)上的信息素量为则按照精英信息素矩阵选择转移节点的公式为：

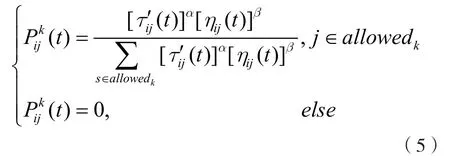
按照基本蚁群算法边上信息素进行转移节点的蚂蚁选择边的公式为：

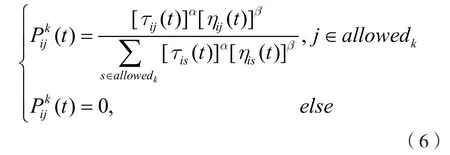
3.2 信息素的奖励促进机制

蚂蚁每完成一次搜索会找到一条最优路径，蚁王将最优路径与之前搜索到的全局最优路径作比较，如果新搜索到的全局最优解最优，则以其取代之前的全局最优路径。

所有蚂蚁进行一次搜索路径后，各边上信息素的更新公式依式（2）、式（3）和式（4）计算。

本文采用最大最小蚂蚁系统将路径上的信息素设置在一定范围内。设信息素的量控制在[tmin,tmax]范围内。当路径上的信息素更新完毕后，按以下公式进行调整：

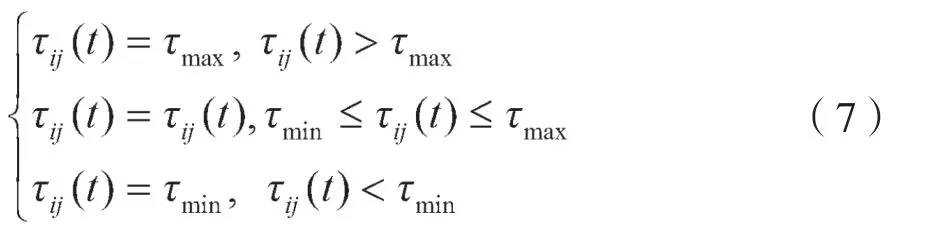
蚂蚁每完成一次迭代循环搜索后，就将路径存储到蚁王中；蚁王将此次搜索到的路径值与之前搜索到的存储路径值作比较，如果新搜索到的路径解优于之前搜索到的最优解，则以这条代替之前的全局最优路径。蚂蚁在进行循环状态转移时，为了使其他蚂蚁在寻路时更好地选择此路径，需要将这条路径上的信息素浓度增大，以进一步增强蚁王搜索过程的指导性，使蚂蚁的搜索更集中于当前所找出的全局最优路径上，进而加快收敛速度。

设当所有蚂蚁进行搜索巡游后，只对当前搜索到的前e(t)个较优解路径进行精英信息素矩阵对应边上进行更新。精英信息素矩阵边上信息素更新公式为：

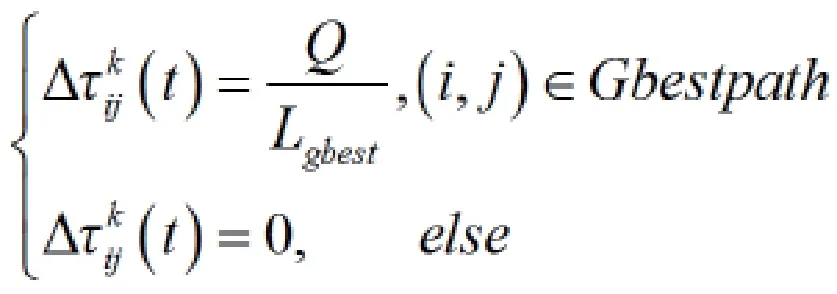
当所有的蚂蚁完成一次搜索后，进行信息素的更新。信息素的更新采用较优路径更新策略。较优路径包括两部分：（1）当前迭代最优解的路径；（2）蚂蚁在当前迭代搜索到解的路径比自己最优解更优的路径。路径（1）信息素的更新，能够使局部最优路径信息素保留，促使以后蚂蚁的搜索方向集中于较优方向。路径（2）信息素的更新，能够使本次搜索成绩较好的蚂蚁的经验在群体间进行交流，有利于在下一次迭代搜索中发现更好的解。

设当所有蚂蚁第t次迭代搜索路径后，当前迭代得到的最优解为Literbest(t)，此时全局最优解为Lgbest。

若Literbest(t)＜Lgbest，则m(t)=m(t)+θ1，e(t)=e(t)+θ2，w(t)=w(t)+θ3；

若Literbest(t)≥Lgbest，则m(t)=m(t)-θ1，e(t)=e(t)-θ2，w(t)=w(t)-θ3。

其中，θ1、θ2、θ3均为大于零的参数。

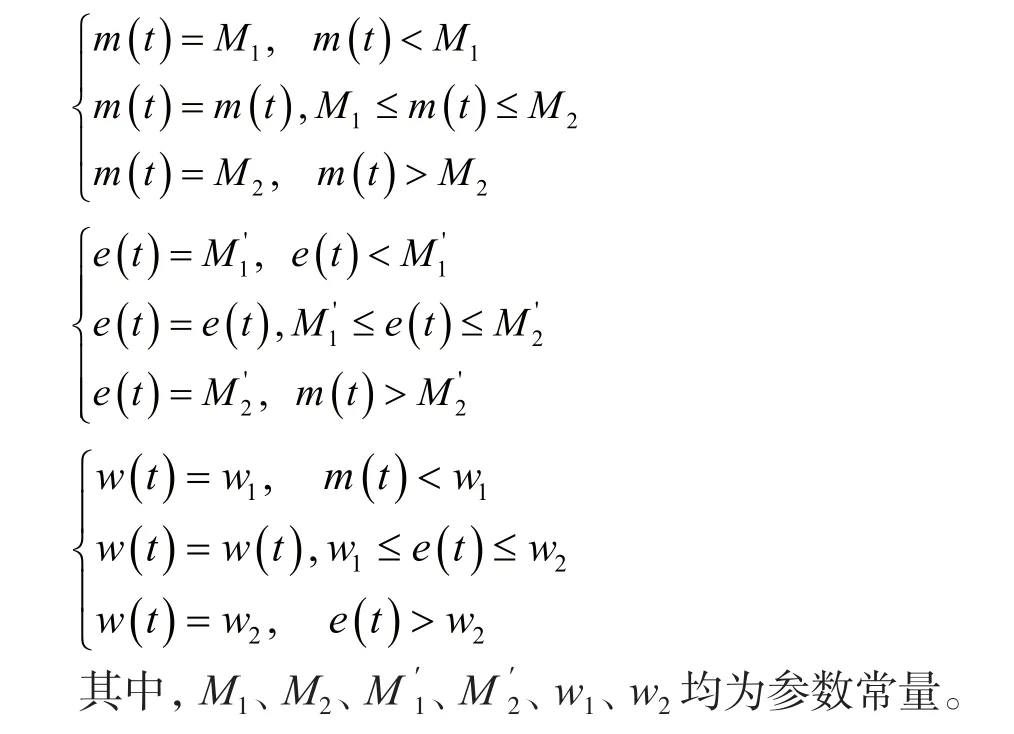
该算法关键在于蚁王对蚂蚁的调配。当一次迭代搜索完成后，判断当前迭代得到的迭代最优解与全局最优解之间的关系。若迭代最优解优于全局最优解，则加大e(t)的数量，即加大精英信息素矩阵中优质解路径更新的数量，那么精英信息素矩阵中信息素的分布表示当前较优质解的分布。同时，要加大m(t)的数量，表示下一次搜索将加大在精英信息素矩阵进行搜索蚂蚁的数量，有利于蚂蚁能够在表示较优解的矩阵发现更好的解。此外，需增加进行变异操作蚂蚁的数量w(t)，以加大对当前算法搜索到的优质解的变异操作，从而对优质解进行变动，以获得更优的解。

若迭代最优解优于全局最优解，即全局最优解不变，则减少e(t)、m(t)、w(t)的数量，以防止劣质解对算法搜索造成干扰。

蚁群中有一部分蚂蚁按照路径上的信息素进行搜索，且该路径上的信息素量置于一定的范围内，以防止由于精英信息素蚂蚁进行搜索而造成的停滞现象。

4 改进蚁群算法在QoS组播中的应用

Qos组播数学模型：计算机网络表示为一个带权图G=(V,E)，其中V代表节点集合，E代表节点间的链路集合，|V|、|E|分别为节点个数与链路个数。假设组播的发送节点s∈V，接收节点集M⊆V-{s}；组播树T是G的子图，VT⊆V，TEE⊆。T中存在由发送点到任意接收的点di的一条路径可表示为p(s,di)，则对于p(s,di)的任意一条链路e∈p(s,di)、顶点n∈p(s,di)，该路由的代价、时延、延时抖动、丢包率各度量函数分别为：延时：

组播QoS多约束路由是符合时延、延时抖动、带宽、丢包率属性的要求下，使组播树的代价最小。描述如下：

其中，D、Dj、B、Pl分别为约束条件属性值。此时，各蚂蚁选择路径公式中ηij(t)为1/Cost(i,j)。

进行变异操作的蚂蚁进行如下操作：

从蚁王保存的当前较优的g个组播树随机选取一个组播树T。随机选择这个组播树的一个目的节点di，则变异操作的蚂蚁将从源节点s到目的节点di进行移动。

此时，蚂蚁的路径选择公式为：

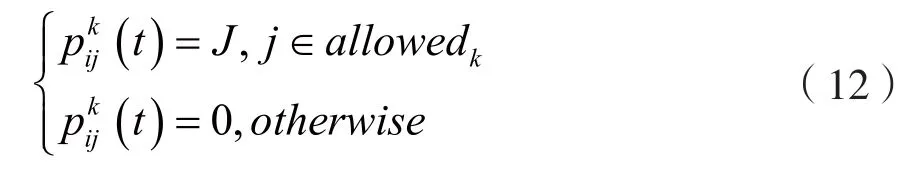
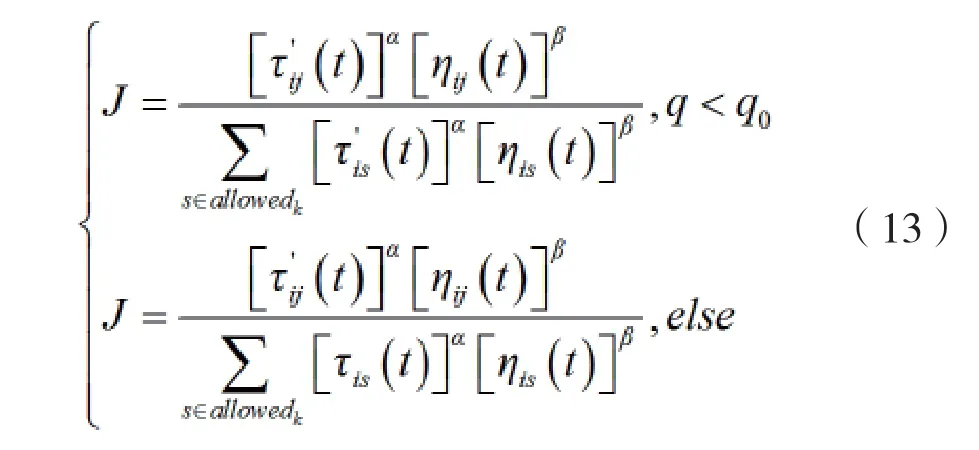
其中，q∈(0,1)为随机数，q0为概率，为一个参数。

此时，蚂蚁操作的蚂蚁将按一定的概率在精英解信息素矩阵表示的信息素量或按边上的信息素量进行选择路径。

5 仿真实验结果与分析

仿真实验环境：采用matlab 7.8，应用Salam拓扑算法随机生成网络拓扑图，如图2所示。

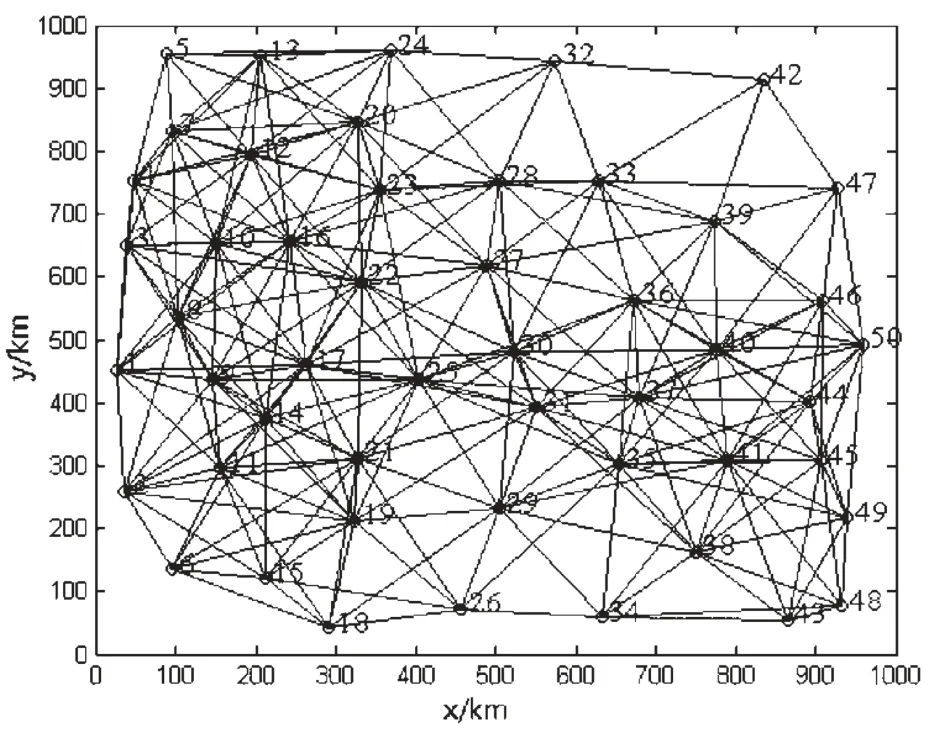
图2 网络拓扑

其中，网络各边的参数见表1。

表1 网络参数取值范围

假设仿真实验各参数：蚂蚁数量M=40，α=1，β=2，ρ=0.1，tmin=0.01，tmax=3，θ1=2，θ2=1，θ3=1，q0=0.7，g=3，m(0)=10，w(0)=4，e(0)=3，M1=5，迭代最大次数Nc=300。网络服务质量各参数[B,D,Dj.Pl]要求为[40,150,60,10e-3]。

两种算法每次路由请求实验进行100次，则实验结果见表2。

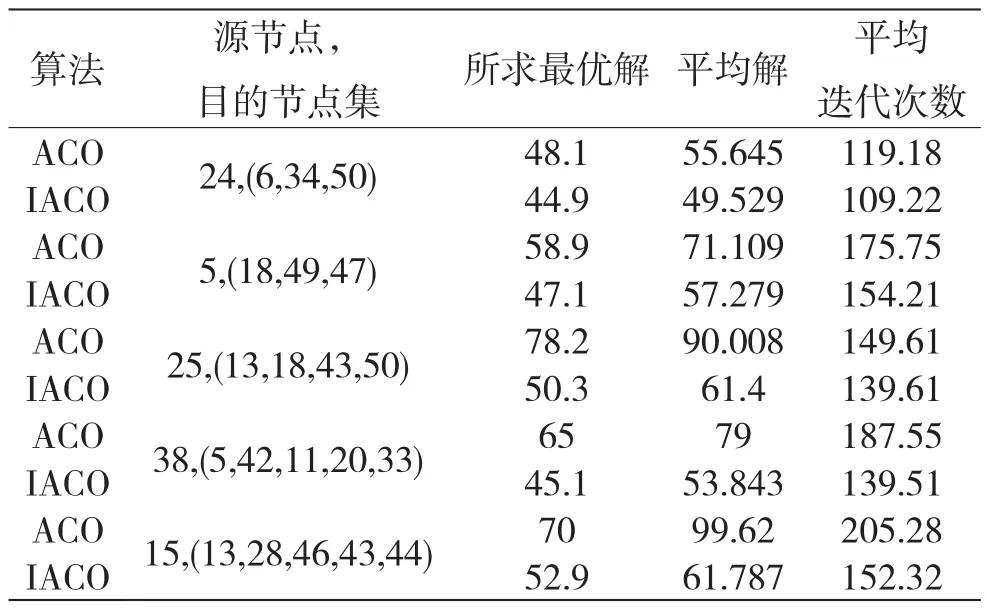
表2 基本蚁群算法和改进蚁群算法的实验结果

设第k次试验中第t轮迭代搜索后，得到的全局最优解为总共n次实验，第t轮迭代搜索后，得到的全局最优解的平均值为：

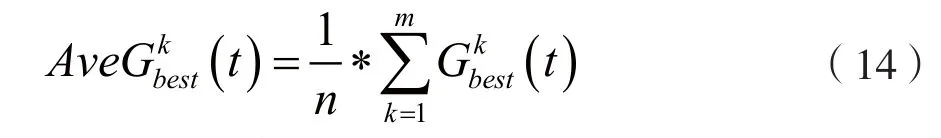
以路由请求{25,(13,18,43,50)}{38,(5,42,11,20,33)}为例，比较基本与改进的蚁群算法。当实验次数n=100时，两种路由请求下，所求组播树代价全局最优解的平均值(t)进化曲线分别如图3、图4所示。

由图3、图4中的平均最优代价曲线可以看出，改进蚁群算法在全局最优的进化过程中，搜索到组播树的代价明显优于基本蚁群算法。例如，设源节点s=18，当目的节点数量不断增加时，比较两种算法多次实验所求组播树代价，结果如图5所示。这里的代价值是多次实验的平均值，实验次数为100次。

图3 25,(13,18,43,50)路由请求组播树平均最优代价进化曲线

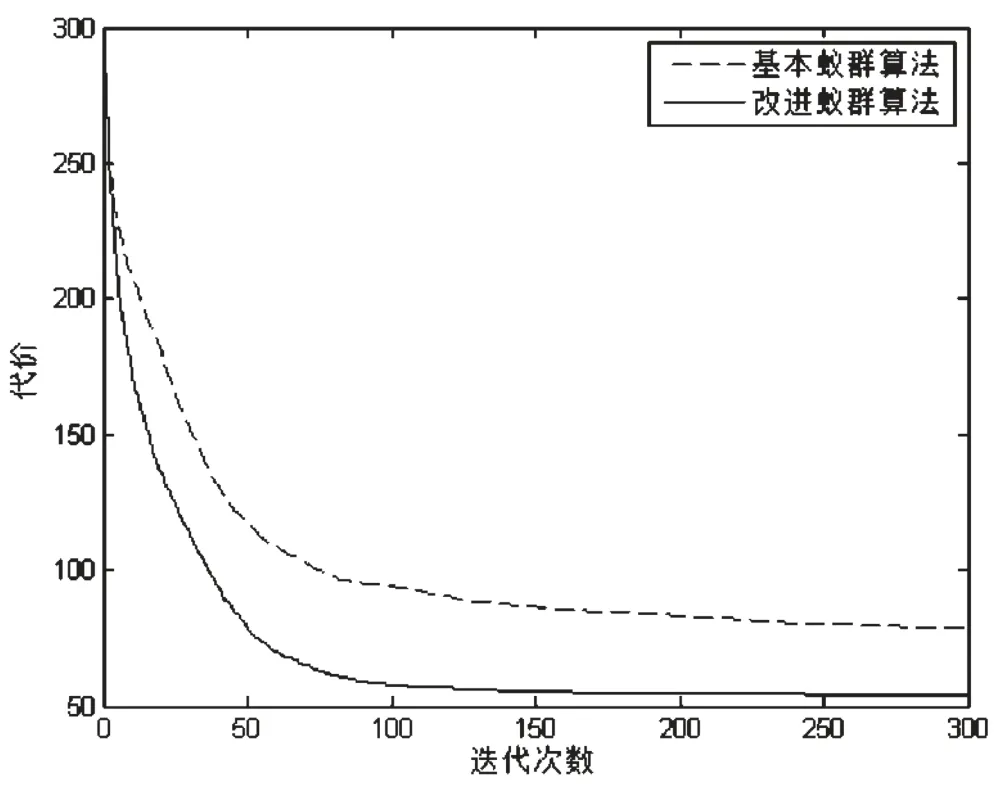
图4 38,(5,42,11,20.33)路由请求组播树平均最优代价进化曲线

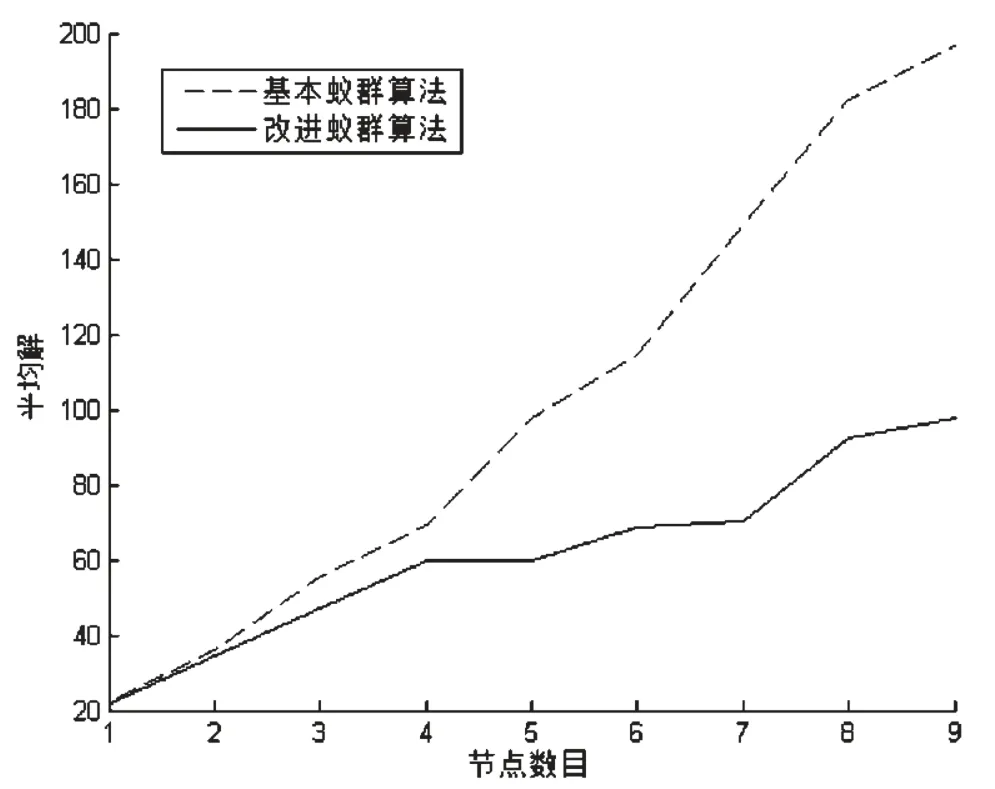
图5 两种算法的组播树代价

6 结 语

本文在基本蚁群算法的基础上，提出了一种新的改进思路。具体的，引进蚁王概念的蚁群算法，借鉴自然蚂蚁无法感知距离的行为，让“蚁王”对蚁群路径的选择策略和过程加以指导和改善。仿真实验结果表明，在蚁群中引入蚁王概念，可使群体搜索过程更加协调有序，且算法能够获得比基本蚁群算法更加优越的性能，提高了全局搜索效率。

[1] DORIGO M,MANIEZZO V,COLORNI A.Ant System: Optimization by a Colony of Cooperating Agents[J]. IEEE Transactions on Systems,Man,and Cybernetics:Part -B,1996,26(01):29-41.

[2] Wang Z,Crowcroft J.Quality-of-Service for Routing Supporting Multimedia Applications[J].IEEE Journal of Selected Areas in Communications,1996,14(07):1228-1234.

[3] 刘洋,王文国.差异化密集蚁群算法与网络QoS路由选择[J].通信技术,2015,48(08):949-953. LIU Yang,WANG Wen-guo.Differentiated Dense Ant Colony Algorithm and Network QoS Routing Selection[J]. Communications Technology,2015,48(08):949-953.

[4] 杨原.基于群智能优化算法的QoS组播路由算法研究[D].西安:西安科技大学,2014. YANG Yuan.Research on QoS Multicast Routing Algorithm based on Swarm Intelligence Optimization Algorithm[D]. Xi’an:Xi’an University of Science and Technology,2014.

[5] 陈峻,沈洁,秦玲等.基于分布均匀度的自适应蚁群算法[J].软件学报,2003,14(08):1379-1387. CHEN Jun,SHEN Jie,QIN Ling,et al.An Adaptive Ant Colony Algorithm based on Equilibrium of Distribution[J]. Journal of Software,2003,14(08):1379-1387.

[6] 邓可,林杰,张鹏.基于信息熵的异类多种群蚁群算法[J].计算机工程与应用,2008,44(36):16-19. DENG Ke,LIN Jie,ZHANG Peng.Multiple Heterogeneous ant Colonies Algorithm based on Information Entropy[J].Computer Engineering and Applications,2008,44(36):16-19.

[7] 张鹏,林杰,邓可.一种基于路径相似度的蚁群算法[J].计算机工程与应用,2007,43(32):28-33. ZHANG Peng,LIN Jie,DENG Ke.Ant Colony Algorithm based on Similarity of Paths[J].Computer Engineering and Application,2007,43(32):28-33.

[8] 姜秋霞.混合蚁群算法及其应用研究[D].上海:同济大学,2008. JIANG Qiu-xia.Research on Hybrid Ant Colony Algorithm and Its Application[D].Shanghai:Tongji University,2008.

王文国（1960—），男，博士，教授，主要研究方向为网络与信息安全；

樊丽娟（1988—），女，硕士研究生，主要研究方向为计算机网络。

Modified Ant-Colony Algorithm and Its Application in QoS Multicast Routing

WANG Wen-guo, FAN Li-juan, LIU Yang
(Dept. of Info. Science & Engineering, Qufu Normal University, Rizhao Shandong 276826, China)

Multicast routing and QoS(Quality of Service) are two important topics of present Internet research. QoS multicast routing, focused to select an optimized multicast routing tree with sufficient resources to meet the requirement of customers, is a typical NPC complete multi-objective optimization problem. The traditional ant-colony algorithm is modified with the introduction of a “queen” concept, thus to help in storage, sorting, and selecting of paths. Meanwhile, the elitist pheromone matrix is used as a strategy to update related pheromone, so as to speed up convergence of the algorithm. Simulation with Matlab indicates that, this new method could achieve much better performance than the basic ant-colony algorithm.

ant-colony algorithm; QoS multicast routing; elitist pheromone; queen

TP311

A

1002-0802(2016)-12-1642-06

10.3969/j.issn.1002-0802.2016.12.013

2016-08-22

2016-11-16 Received date:2016-08-22;Revised date:2016-11-16

国家人事部高层次留学人员回国工作资助项目（No.200461）

Foundation Item:National High Level Talents Attracting Program of China(No.200461)